Nonmetal-to-metal transition in dense fluid helium
Dedicated to the memory of Vladimir E. Fortov (1946-2020).
Funding information: Deutsche Forschungsgemeinschaft, 2440/2; Universitaet Rostock
Abstract
The nonmetal-to-metal transition in dense fluid helium is discussed, which has been, in analogy to metallization of hydrogen, predicted as first-order plasma phase transition using chemical models for the equation of state and plasma composition. However, recent ab initio simulations performed for dense fluid helium indicate that this transition is continuous in the considered regime, without a density jump and latent heat as characteristic of a first-order phase transition. Implications for some astrophysical plasmas are discussed.
1 INTRODUCTION
This article is devoted to the memory of Vladimir E. Fortov (1946–2020)[1] who has given pioneering contributions to the physics of nonideal plasmas, in particular to the equation of state (EOS) data, the phase diagram, and the electrical conductivity of matter at extreme conditions. The plasma phase transition (PPT) and the behaviour of dense helium had always sparked his interest.
A PPT is predicted when a nonmetal-to-metal transition in dense plasmas occurs abruptly. The latter phenomenon is also known as metallization, in particular for hydrogen. Initially, metallization of solid hydrogen was predicted at high pressures by Wigner and Huntington in 1935.[2] Norman and Starostin[3] proposed a first-order phase transition in partially ionized plasmas (PIP) in 1968, in analogy to the competing effects of the long-range attractive forces and the short-range repulsive forces in van der Waals systems; see also Norman and Saitov.[4] The existence of a PPT and its slope in pressure–temperature space are not only important for the shape of the high-pressure phase diagram but also for astrophysical applications such as the interior structure of gas giant planets[5] and their dynamo region.[6]
Inspired by Vladimir E. Fortov, Russian institutes provided essential contributions to this fundamental problem over decades. A multitude of experiments aimed to determine the EOS and the electrical conductivity of hydrogen, helium, and other elements and compounds via sophisticated explosively driven shock-wave experiments.[7-14] Other experiments on the metallization of dense fluid hydrogen were performed with gas guns,[15] Sandia's Z machine,[16] and high-power lasers such as National Ignition Facility,[17] and in the solid phase using diamond anvil cells.[18] The exact location of the metallization transition in solid and liquid hydrogen is still under lively debate.
Numerous theoretical studies investigated the behaviour of dense hydrogen plasma and the location of the PPT. For instance, Ebeling and coworkers calculated the EOS of partially ionized hydrogen plasmas via chemical models considering dissociation and ionization.[19-22] Similar models were developed by Saumon and Chabrier[23-26] and by Ross[27, 28] using fluid perturbation or variational theory; see also Juranek and Redmer[29] and Juranek et al.[30] The PPT in H and H–He mixtures has also been studied using said chemical models[31] and path integral Monte Carlo simulations.[32]
Based on these elaborate chemical models, Förster et al.[33] and Kahlbaum and Förster[34] calculated the EOS and the ionization degree of dense helium plasma. The behaviour of helium is expected to be simpler than that of hydrogen because no molecular phase exists and the rather complex dissociation equilibrium can be neglected. However, besides single ionization (He+), also double ionization (He2+) occurs so that the plasma is composed of electrons and an ionic mixture. The chemical picture for H and He has also been discussed within the framework of SAHA-family models.[35]
Förster et al.[33] predicted two subsequent PPTs, one for each ionization stage. Recent ab initio simulations of dense fluid helium employed density functional theory molecular dynamics (DFT-MD),[36] finding a smooth transition to a metallic state at high pressures. No signs of a first-order PPT, as predicted by Förster et al.,[33] were observed, that is, neither a density jump nor a jump in the electrical conductivity. We conclude that the nonmetal-to-metal transition in dense fluid He is continuous.
2 CHEMICAL MODELS
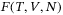 as function of the temperature
as function of the temperature 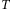 , the volume
, the volume 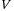 , and the total particle number
, and the total particle number 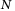 :
:
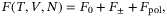 (1)
(1)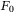 denotes the contribution of neutral particles (atoms, molecules),
denotes the contribution of neutral particles (atoms, molecules), 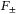 the contribution of charged particles (electrons, ions) interacting via the Coulomb potential, and
the contribution of charged particles (electrons, ions) interacting via the Coulomb potential, and 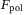 the interaction between charged and neutral particles via a polarization potential. The total particle number is the sum over all species in a partially ionized helium plasma, that is,
the interaction between charged and neutral particles via a polarization potential. The total particle number is the sum over all species in a partially ionized helium plasma, that is, 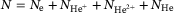 . The ionization reactions are described by coupled mass action laws, which are derived from chemical equilibrium conditions:
. The ionization reactions are described by coupled mass action laws, which are derived from chemical equilibrium conditions:
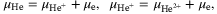 (2)
(2)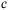 is self-consistently derived from the free energy (1) according to
is self-consistently derived from the free energy (1) according to 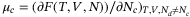 . The plasma composition can be characterized by the ionization degree,
. The plasma composition can be characterized by the ionization degree, 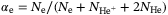 , or the mean charge of heavy particles,
, or the mean charge of heavy particles, 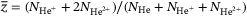 .
.Chemical models rely on approximate expressions for the various contributions to the free energy (1). For instance, the neutral component is usually treated within fluid variational theory,[27-30] which determines the free energy 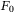 based on effective interaction potentials between the neutral particles relative to a hard or soft core reference system. For the plasma component composed of electrons and singly and doubly charged helium ions, efficient Padé formulae have been developed[33] for
based on effective interaction potentials between the neutral particles relative to a hard or soft core reference system. For the plasma component composed of electrons and singly and doubly charged helium ions, efficient Padé formulae have been developed[33] for 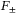 , which interpolate between the known analytic expressions for low- and high-density plasmas, that is, Debye–Hückel and Thomas–Fermi theory. The polarization contribution
, which interpolate between the known analytic expressions for low- and high-density plasmas, that is, Debye–Hückel and Thomas–Fermi theory. The polarization contribution  is important in the partially ionized domain and calculated via the second virial coefficient with respect to a screened polarization potential.[37]
is important in the partially ionized domain and calculated via the second virial coefficient with respect to a screened polarization potential.[37]
Förster et al.[33] have calculated the EOS of dense helium plasma (1) and considered the two ionization reactions (2) self-consistently. Due to the large difference between the first (24.587 eV) and second ionization energies (54.418 eV), they observed extended regions of neutral helium fluid and of singly and doubly ionized helium plasma, respectively, depending on density and temperature. Consequently, their chemical model predicts two distinct PPTs at high pressures: the first model due to the ionization of neutral helium to He+, and the second model due to a subsequent ionization to He2+. Förster et al.[33] located the critical point C1 for the corresponding coexistence curve between the neutral and singly ionized fluids at around 35,000 K and 660 GPa (first PPT). They further predict a coexistence curve between the single-fold and twofold ionized fluids (second PPT), which ends in a second critical point C2 at  K and 10 TPa. The corresponding P–T phase diagram is shown in Figure 1. Although a strong increase of ionization and electrical conductivity has been observed in the region of the first PPT,[39] a first-order phase transition has yet to be verified experimentally.
K and 10 TPa. The corresponding P–T phase diagram is shown in Figure 1. Although a strong increase of ionization and electrical conductivity has been observed in the region of the first PPT,[39] a first-order phase transition has yet to be verified experimentally.
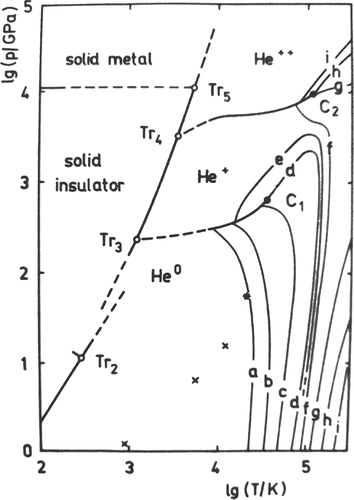
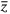 of heavy particles (a, 0.01; b, 0.1; c, 0.5; d, 0.9; e, 1.0; f, 1.1; g, 1.5; h, 1.9; i, 1.99). Crosses denote single shocks along the Hugoniot curve and the asterisk a double-shock point
of heavy particles (a, 0.01; b, 0.1; c, 0.5; d, 0.9; e, 1.0; f, 1.1; g, 1.5; h, 1.9; i, 1.99). Crosses denote single shocks along the Hugoniot curve and the asterisk a double-shock point3 AB INITIO METHOD
3.1 DFT-MD simulations
DFT[40-42] introduces the ground-state electron density as central quantity to calculate observables of the quantum mechanical electronic system. The Born–Oppenheimer approximation[43] decouples the computation of the electronic and ionic systems. A given ionic distribution results in a corresponding ground-state electron density. The resulting Hellman–Feynman forces, derived from the Born–Oppenheimer energy surface, act on the ions and contribute to their temporal evolution within classical MD. Finite temperatures lead to a thermal excitation of the electronic bands according to the Fermi–Dirac statistics.[44] A Nosé–Hoover thermostat[45, 46] couples the ionic system with a heat bath, resulting in the description of a canonical ensemble and an ionic velocity distribution described by Boltzmann statistics. All unknown contributions of the electronic system are approximated by the exchange–correlation (xc) functional. Among the large number of approximations to the xc functional, we use the formulation of Perdew, Burke, and Ernzerhof.[47] We employ DFT-MD as implemented in the plane-wave code VASP,[48-51] a sampling of the Brillouin zone with the Baldereschi mean value point[52] or a more elaborate Monkhorst–Pack set,[53] and pseudopotentials utilizing the projector-augmented wave (PAW) method.[54]
3.2 Band gap calculations
In order to evaluate the behaviour of the band gap in the liquid, we calculate histograms of the electronic band energies in thermodynamic equilibrium, comparable to a study of the band gap closure of dense solid helium.[55] We employ a similar definition of the band gap as of Stixrude and Jeanloz[56]: The band gap is the energy range in the vicinity of the mean chemical potential where the occupancy is less than 1% of the maximal occupancy of the valence band. We find that the method using histograms as described earlier and in Preising and Redmer[36] and Monserrat et al.[55] gives the most reliable results compared to other approaches to the band gap also discussed in Preising and Redmer.[36] Usually, band gaps are calculated from snapshots of atomic configurations obtained from DFT-MD simulations. However, we find that we cannot obtain converged results from snapshot-based calculations and instead have to evaluate the statistical data from several thousand DFT-MD time steps. Figure 2 consists of our results[36] of the band gap closure with the histogram method in the liquid.
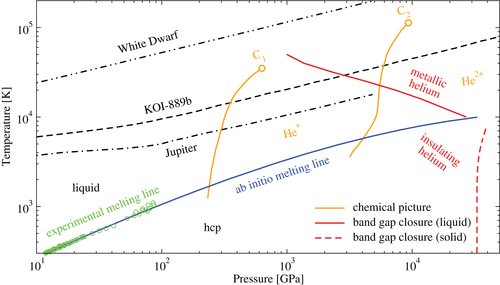
The ab initio melting line of dense helium[57] clarifies the location of the liquid regime. Due to the higher order in the solid, the corresponding band gap[55] closes at higher pressures compared to the more disordered liquid.
The slope of the band gap closure from DFT-MD in the liquid is perpendicular to the ionization stages calculated by Förster et al.[33] This highlights the significance of correlation and quantum effects in this extreme density regime that cannot be taken into account by chemical models.
According to the results of our approach to the band gap, the deep interior of Jupiter[58] does not exhibit conditions under which metallic helium could exist. However, metallic helium is predicted under the interior conditions of the brown dwarf KOI-889b.[59] At higher temperatures, our method to calculate the band gap might predict metallic helium under the interior conditions of white dwarfs.[60]
3.3 Direct current conductivity
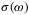 within the Kubo–Greenwood formalism,[61-65]
within the Kubo–Greenwood formalism,[61-65]
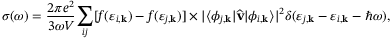 (3)
(3) on the wavefunction
on the wavefunction 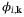 of the ith band at k-point
of the ith band at k-point 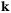 , weighted by the Fermi–Dirac occupation
, weighted by the Fermi–Dirac occupation 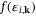 corresponding to the energy
corresponding to the energy 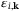 , summed over the bands
, summed over the bands 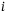 and
and 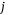 , and multiplied with a prefactor containing the elementary charge
, and multiplied with a prefactor containing the elementary charge 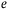 , the frequency
, the frequency 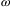 , and the supercell volume
, and the supercell volume 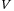 .
.To evaluate the DC conductivity, we calculate the low-frequency limit of 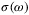 . We employ the number of atoms, atomic snapshots, number of bands per atom,
. We employ the number of atoms, atomic snapshots, number of bands per atom, 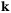 -point sampling, and PAW according to the convergence tests documented in Reference [66]. Figure 3 displays our results[36] compared to the results of a Drude model fitted to experimental data on reflectivity,[67] our ab initio results for the same data set,[70] ab initio predictions for higher densities,[56, 68, 69] and the minimum metallic conductivity according to the Mott criterion:
-point sampling, and PAW according to the convergence tests documented in Reference [66]. Figure 3 displays our results[36] compared to the results of a Drude model fitted to experimental data on reflectivity,[67] our ab initio results for the same data set,[70] ab initio predictions for higher densities,[56, 68, 69] and the minimum metallic conductivity according to the Mott criterion: 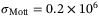 S/m.
S/m.
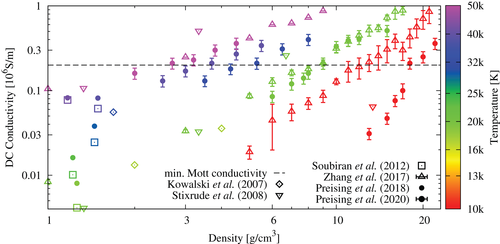
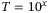 K, with
K, with 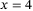 , 4.3, 4.5, 4.6, and 4.7, respectively; see Preising and Redmer.[36] The dashed black line represents the minimum metallic conductivity according to the Mott criterion at zero temperature
, 4.3, 4.5, 4.6, and 4.7, respectively; see Preising and Redmer.[36] The dashed black line represents the minimum metallic conductivity according to the Mott criterion at zero temperatureAt the lowest temperatures, the isotherms exhibit a strong increase in DC conductivity with density that we do not observe at higher temperatures. This feature is less pronounced in the results of Zhang et al.[69] The increase occurs around the minimum metallic conductivity according to the Mott criterion. It probably originates from thermal excitations, which significantly lower the electronic resistance, thereby increasing the conductivity. The observed behaviour coincides with that of expanded fluid metals[71, 72] and noble gases.[73, 74]
We do not observe a density jump indicating a first-order phase transition in the DC conductivity over the density. Instead, the DC conductivity continuously increases with density and temperature. In contrast, an abrupt nonmetal-to-metal transition has been observed in dense fluid hydrogen,[16, 17] which is perhaps of first order below a second critical point at about 2,000 K, and accompanied by jumps in the density and the DC conductivity.[75, 76]
3.4 Astrophysical implications
Like other conductive and convective constituents of planetary and stellar interiors, liquid metallic helium would contribute to the dynamo and the heat transport of the astrophysical object. The metallization pressure of helium has a direct impact on the cooling behaviour of helium-rich white dwarfs.[77-79] In addition to the convective heat transport, the liquid metallic phase also transfers heat via electron transport, thereby increasing the heat conductivity. A solid helium layer transports heat via phonons, while a metallic solid layer additionally conducts heat via electron transport. Therefore, higher metallization pressures would result in slower heat transfer, which decreases the cooling rate and luminosity of the respective astrophysical object,[80] while the opposite holds true for lower metallization pressures.
To infer the age of a cosmic region, one can count the number of white dwarfs with a certain luminosity. The higher the number of cold and dim white dwarfs, the older the respective region and vice versa.[81, 82] Therefore, as discussed earlier, higher metallization pressures would result in dimmer white dwarfs, leading to a higher estimated age of cosmic regions. The use of white dwarfs as cosmochronometers, and in particular their conductive opacity, has been recently discussed.[83]
4 CONCLUSION
Our ab initio simulations clearly show a continuous nonmetal-to-metal transition in dense fluid helium at very high pressures in the TPa range (see Figure 3). We do not find evidence for a first-order phase transition (PPT). Earlier predictions for a PPT derived from chemical models,[33] see Figure 1, may be traced back to the approximate treatment of correlations and quantum effects in the corresponding free energy expressions, which induce the thermodynamic instability known as PPT. However, future experiments should probe the relevant region 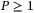 TPa and
TPa and 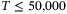 K in order to confirm our result (see Figure 2).
K in order to confirm our result (see Figure 2).
The striking difference to the metallization transition in dense fluid hydrogen, which is most likely of first order below a second critical point at about 2,000 K,[16, 17] is due to the much higher ionization energy (24.587 eV in He vs. 13.602 eV in H) and the continuously increasing melting line in helium (see Figure 2). For instance, at 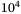 GPa, we predict the nonmetal-to-metal transition at about
GPa, we predict the nonmetal-to-metal transition at about 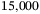 K, which is too high to be of first order.
K, which is too high to be of first order.
ACKNOWLEDGEMENTS
We thank Valdimir E. Fortov for numerous and always dedicated discussions on the properties of dense plasmas and his continuing interest in our theoretical work. R. R. thanks Victor Mintsev, Victor Gryaznov, Vladimir Ternovoi, Igor Iosilevskiy, Vladimir Filinov, William Nellis, Peter Edwards, Friedrich Hensel, Werner Ebeling, Wolf-Dietrich Kraeft, and Gerd Röpke for many inspiring discussions on this topic. We acknowledge support by the DFG via the Research Unit FOR 2440/2. The numerical calculations were performed at the High-Performance Computing Center (ITMZ) of the University of Rostock and the North-German Supercomputing Alliance (HLRN) via contract mvp00012. Open Access funding enabled and organized by Projekt DEAL.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




