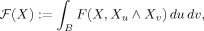Plateau's problem for parametric double integrals: I. Existence and regularity in the interior†
In memory of Jürgen Moser, teacher and friend
Abstract
We study Plateau's problem for two-dimensional parametric integrals
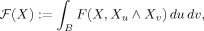
In memory of Jürgen Moser, teacher and friend
We study Plateau's problem for two-dimensional parametric integrals