Computational and Mathematical Methods
Volume 3, Issue 6 e1213
SPECIAL ISSUE PAPER
Full Access

A new family of 𝒜 − acceptable nonlinear methods with fixed and variable stepsize approach

Sania Qureshi, 

Corresponding Author

Sania Qureshi

Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro, Pakistan

Department of Mathematics, Near East University TRNC, Mersin 10, Turkey

Correspondence Sania Qureshi, Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro 76062, Pakistan.

Email: [email protected]

Search for more papers by this author
Amanullah Soomro, 

Amanullah Soomro

Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro, Pakistan

Search for more papers by this author
Evren Hınçal, 

Evren Hınçal

Department of Mathematics, Near East University TRNC, Mersin 10, Turkey

Search for more papers by this author
First published: 12 November 2021
https://doi.org/10.1002/cmm4.1213
Citations: 7

Abstract

Solving stiff, singular, and singularly perturbed initial value problems (IVPs) has always been challenging for researchers working in different fields of science and engineering. In this research work, an attempt is made to devise a family of nonlinear methods among which second- to fourth-order methods are not only 𝒜 − stable but 𝒜 − acceptable as well under order stars' conditions. These features make them more suitable for solving stiff and singular systems in ordinary differential equations. Methods with remaining orders are either zero- or conditionally stable. The theoretical analysis contains local truncation error, consistency, and order of accuracy of the proposed nonlinear methods. Furthermore, both fixed and variable stepsize approaches are introduced wherein the latter improves the performance of the devised methods. The applicability of the methods for solving the system of IVPs is also described. When used to solve problems from physical and real-life applications, including nonlinear logistic growth and stiff model for flame propagation, the proposed methods are found to have good results.

1 Introduction

Consider the initial value problem (IVP) given below:
y ′ = f ( t , y ( t ) ) , y ( t 0 ) = y 0 , f , y ∈ ℝ n & t ∈ [ t o , t n ] , t 0 , t n ∈ ℝ , ()
where t 0 and t n are the starting and final values of t over the integration interval [ t 0 , t n ] . Traditionally, the methods called classical single-step Runge–Kutta and linear multistep methods are specially developed for solving problems of the type (1). These traditional methods usually fail when it comes to solutions of the problems having singularities or oscillatory behavior, or the problems themselves are either stiff, oscillatory or singularly perturbed in nature.1-3 Such problems are ubiquitous in various fields of science and engineering, including Van der Pol oscillator in electrical engineering, spring and damping systems in mechanical engineering, negative resistance oscillatory circuit in electronics, Lorenz system in meteorology, flame propagation in heat transfer, Robertson chemical kinetics problem; and many more.4-6 There is no unified approach to handling such problems from the qualitative and numerical viewpoint.

The emergence of nonlinear methods in solving many kinds of problems under the scalar and vector versions has intrigued many researchers to study more on this topic. Some past and recently published research work on nonlinear methods are.7-15 The analysis of ordinary differential equations is an essential tool for investigating the relationship between various dynamical quantities on which more literature can be found in Reference 16. It is challenging to find the exact solution of differential equation-based models in various situations, mainly when the problem is either nonlinear, stiff, singular, or singularly perturbed. In these conditions, we move toward the nonlinear, trigonometrically-fitted, Runge–Kutta collocation, and BDF-type Chebyshev numerical methods.17-24 After being motivated with research works recently carried out for devising or modifying nonlinear numerical methods that are suitable for stiff and singular IVPs, we attempt to derive a new family of nonlinear methods with second to the fourth-order of accuracy, and 𝒜 − stability feature of the methods is also established. This article first derives the methods with constant step size and later formulates the proposed methods with a variable stepsize approach.

It may also be noted before starting formal analysis that whether the initial value problem (1) under consideration has a unique solution or not. The “existence” and “uniqueness” of solutions are essential things to study to solve problems and make predictions. Following the Lipschitz condition is the most frequently used criterion among various existing strategies to test the existence of a unique solution to (1).

Definition 1.The function f : [ t 0 , t n ] × ℝ N → ℝ N is said to fulfill the Lipschitz condition in its dependent variable if there exists a positive constant M, commonly called the Lipschitz constant, such that for any t ∈ [ t 0 , t n ] and Y , U ∈ ℝ N , | | f ( x , Y ) − f ( x , U ) | | ≤ M | | Y − U | | .

Now, the above definition can be employed in the theorem given below.

Theorem 1.Consider an IVP of the form (1) where f : [ t 0 , t n ] × ℝ N → ℝ N is continuous in its independent variable and fulfills the Lipschitz condition in its dependent variable. This approach implies the existence of a unique solution to the IVP (1).

Proof.The proof of the above Theorem 1 can be found in References 25 and 26.

The present article is divided into seven sections as follows: In the Section 1 above, we have discussed the need to devise nonlinear numerical methods for solving IVPs with stiffness, singularities, and singularly perturbed nature. In Section 2, general formulation for the family of nonlinear methods is proposed that leads to having three nonlinear methods with 𝒜 − stability characteristics, whereas methods with remaining orders are found to be either zero- or conditionally stable. Section 3 is concerned with the theoretical analysis of the newly devised family wherein we discuss conventional linear stability, stability with order stars, local truncation errors, and consistency of the proposed nonlinear methods. In Section 4, the applicability of the methods for system of first order ordinary differential equations is discussed. Section 5 is concerned with variable stepsize approach. In Section 6; some stiff, singular, and singularly perturbed IVPs in terms of first-order and system of first-order ordinary differential equations are taken from scientific areas to observe numerical dynamics of the proposed methods in comparison to other methods existing in the literature. In comparison to other methods, a discussion of the obtained results is carried out in the final Section 7.

2 Derivation of Proposed Methods

Most numerical methods for solving IVPs in numerical analysis are derived with a local representation of a polynomial using Taylor's expansion approach. Due to this reason, they do not become capable enough to perform near/at singular points present either in the ODE itself or in its theoretical solution. This gap was filled by many researchers who recently came up with nonlinear numerical methods that use a rational approximation for the unknown theoretical solution of the stiff and the singularly perturbed models. After being motivated with the recently published research27-34 in this dynamic area, we propose the following rational approximation y n + 1 for the theoretical solution y ( t n + 1 ) to the IVP given in (1):
y n + 1 = α + β h y n + ∑ j = 1 m γ j h j , ()
where α , β and γ j ( j = 1 , 2 , 3 , … , m ) are undetermined parameters.

2.1 First-order method

To obtain a new method of first-order, we substitute the value of m = 0 in (2) so the nonlinear type of approximation is obtained as follows:
y n + 1 = α + β h y n , ()
where α and β are undetermined parameters that depend on the known values at t n and must be determined. Applying the Taylor expansion for the equation in (3) about t n and collecting the terms in powers of h, we get
ℒ [ y ( t ) ; h ] LMZS 1 = ( − α + y ( t n ) ) + ( y ′ ( t n ) − β y ( t n ) ) h + ( y ″ ( t n ) 2 ) h 2 + 𝒪 ( h 3 ) . ()
In order to get a method of first-order, the coefficients until the term containing h in (4) must be equated to zero. By doing so, we obtain the following linear system of equations
− α + y ( t n ) = 0 , y ′ ( t n ) − β y ( t n ) = 0 . ()
Solving the above linear system in (5) for α and β , one gets
α = y ( t n ) , β = y ( t n ) y ′ ( t n ) . ()
Under the local assumption, we have y ( q ) ( t n ) = y n ( q ) , ( q = 0 , 1 ) . From Equations (3) and (6), we formulated the first order L M Z S 1 as given below
y n + 1 = y n + y n ′ h . ()

It is worth noting that the method devised in (7) turns out to be the well-known forward Euler's method whose zero-stability is easy to verify. Since the method (7) is a well-established method in the available literature, therefore we will not be discussing it in detail in our research analysis. Instead, our primary focus will remain on developing nonlinear methods and possessing strong stability characteristics, making them suitable for stiff and singularly perturbed problems. Moreover, we use the notation “ LMZS 1 ” that stands for the first-order linear method with zero-stability.

2.2 Second-order nonlinear method

To obtain a new nonlinear method of second-order, we substitute the value of m = 1 in (2) as follows:
y n + 1 = α + β h y n + γ 1 h , ()
where α , β , and γ 1 are undetermined parameters that depend on the known values at t n and must be formulated. Applying the Taylor expansion for the equation in (8) about t n and collecting the terms in powers of h, we get
ℒ [ y ( t ) ; h ] NMAS 2 = ( − α + y ( t n ) ) + ( y ′ ( t n ) − β y ( t n ) ) h + ( 1 2 y ″ ( t n ) + β γ 1 y ( t n ) 2 ) h 2 + ( 1 6 y ″ ′ ( t n ) − β γ 1 2 y ( t n ) 3 ) h 3 + O ( h 4 ) . ()
In order to get a method of second-order, the coefficients until h 2 in (9) must be equated to zero. By doing so, we obtain the following nonlinear system of equations:
− α + y ( t n ) = 0 , y ′ ( t n ) − β y ( t n ) = 0 , y ″ ( t n ) 2 + β γ 1 y ( t n ) 2 = 0 , ()
where the term y ″ ′ ( t n ) 6 − β γ 1 2 y ( t n ) 3 ≠ 0 . Solving the above nonlinear system for α , β and γ 1 , one gets
α = y ( t n ) , β = y ( t n ) y ′ ( t n ) , γ 1 = − y ″ ( t n ) y ( t n ) 2 y ′ ( t n ) y ( t n ) . ()
Under the local assumption, we have y ( q ) ( t n ) = y n ( q ) ( q = 0 , 1 , 2 ) . Based on Equations (8) and (11), we have formulated the following second-order method:
y n + 1 = y n y n ″ h − 2 y n ′ 2 h − 2 y n y n ′ y n ″ h − 2 y n ′ . ()

We use the notation “ N M A S 2 ” that stands for the above second-order nonlinear method with 𝒜 -stability.

2.3 Third-order nonlinear method

To obtain a new nonlinear method of second-order, we substitute the value of m = 2 in (2) as follows:
y n + 1 = α + β h y n + γ 1 h + γ 2 h 2 , ()
where α , β , γ 1 , and γ 2 are undetermined parameters that can depend on the known values at t n and must be formulated. Applying the Taylor expansion for the equation in (13) about t n and collecting the terms in powers of h, we get
ℒ [ y ( t ) ; h ] NMAS 3 = ( − α + y ( t n ) ) + ( y ′ ( t ) − β y ( t n ) ) h + ( 1 2 y ″ ( t n ) + β γ 1 y ( t n ) 2 ) h 2 + ( 1 6 y ″ ′ ( t n ) + β γ 2 y ( t n ) 2 − β γ 1 2 y ( t n ) 3 ) h 3 + ( 1 24 y ( i v ) ( t n ) − 2 β γ 1 γ 2 y ( t n ) 3 + β γ 1 3 y ( t n ) 4 ) h 4 + O ( h 5 ) . ()
In order to get a method of third-order, the coefficients until h 3 in (14) must be equated to zero. By doing so, we obtain the following nonlinear system:
− α + y ( t n ) = 0 , y ′ ( t n ) − β y ( t n ) = 0 , y ″ ( t n ) 2 + β γ 1 y ( t n ) 2 = 0 , 1 6 y ″ ′ ( t n ) + β γ 2 y ( t n ) 2 − β γ 1 2 y ( t n ) 3 = 0 , ()
where 1 24 y ( i v ) ( t n ) − 2 β γ 1 γ 2 y ( t n ) 3 + β γ 1 3 y ( t n ) 4 ≠ 0 . Solving the above nonlinear system of equations in (15) for α , β , γ 1 and γ 2 , one gets
α = y ( t n ) , β = y ( t n ) y ′ ( t n ) , γ 1 = − y ″ ( t n ) y ( t n ) 2 y ′ ( t n ) y ( t n ) , γ 2 = − y ( t n ) ( 2 y ′ ( t n ) y ″ ′ ( t n ) − 3 y ″ ( t n ) 2 ) 12 y ′ ( t n ) 2 . ()
Under the local assumption, we have y ( q ) ( t n ) = y n ( q ) ( q = 0 , 1 , 2 , 3 ) . Based on Equations (13) and (16), we have formulated the following third-order nonlinear method:
y n + 1 = y n + 12 h y n ′ 3 h 2 ( 3 y n ″ 2 − 2 y n ′ y n ″ ′ ) − 6 h y n ″ y n ′ + 12 y n ′ 2 . ()

We use the notation “ N M A S 3 ” that stands for the above third-order nonlinear method with 𝒜 -stability.

2.4 Fourth-order nonlinear method

To obtain a new nonlinear method of fourth-order, we substitute the value of m = 3 in (2) as follows:
y n + 1 = α + β h y n + γ 1 h + γ 2 h 2 + γ 3 h 3 , ()
where α , β , γ 1 , γ 2 , and γ 3 are undetermined parameters that can depend on the known values at t n and must be formulated. Applying the Taylor expansion for the equation in (18) about t n and collecting the terms in powers of h, we get
ℒ [ y ( t ) ; h ] NMAS 4 = ( − α + y ( t n ) ) + ( y ′ ( t n ) − β y ( t n ) ) h + ( 1 2 y ″ ( t n ) + β γ 1 y ( t n ) 2 ) h 2 + ( 1 6 y ″ ′ ( t n ) + β γ 2 y ( t n ) 2 − β γ 1 2 y ( t n ) 3 ) h 3 + ( 1 24 y ( i v ) ( t n ) + β γ 3 y ( t n ) 2 − 2 β γ 1 γ 2 y ( t n ) 3 + β γ 1 3 y ( t n ) 4 ) h 4 + ( y ( v ) ( t n ) 120 − 2 β γ 1 γ 2 y ( t n ) 3 + β γ 2 2 y ( t n ) 3 + 3 β γ 2 γ 1 2 y ( t n ) 4 − β γ 1 4 y ( t n ) 5 ) h 5 + O ( h 6 ) . ()
In order to get fourth-order nonlinear method, the coefficients until h 4 in (19) must be equated to zero. By doing so, we obtain the following nonlinear system of equations:
− α + y ( t n ) = 0 , y ′ ( t n ) − β y ( t n ) = 0 , y ″ ( t n ) 2 + β γ 1 y ( t n ) 2 = 0 , 1 6 y ″ ′ ( t n ) + β γ 2 y ( t n ) 2 − β γ 1 2 y ( t n ) 3 = 0 , 1 24 y ( i v ) ( t n ) + β γ 3 y ( t n ) 2 − 2 β γ 1 γ 2 y ( t n ) 3 + β γ 1 3 y ( t n ) 4 = 0 , ()
where y ( v ) ( t n ) 120 − 2 β γ 1 γ 3 y ( t n ) 3 − β γ 2 2 y ( t n ) 3 + 3 β γ 2 γ 1 2 y ( t n ) 4 − β γ 1 4 y ( t n ) 5 ≠ 0 . Solving the above nonlinear system of equations in (20) for α , β , γ 1 , γ 2 , and γ 3 , one gets
α = y ( t n ) , β = y ( t n ) y ′ ( t n ) , γ 1 = − y ″ ( t n ) y ( t n ) 2 y ′ ( t n ) y ( t n ) , γ 2 = y ( t n ) ( 2 y ′ ( t n ) y ″ ′ ( t n ) − 3 y ″ ( t n ) 2 ) 12 y ′ ( t n ) 2 , γ 3 = − y ( t n ) ( 3 y ″ ( t n ) 3 − 4 y ″ ( t n ) y ′ ( t n ) y ″ ′ ( t n ) + y ′ ( t n ) 2 y ( i v ) ( t n ) ) 24 y ′ ( t n ) 3 . ()
Under the local assumption, we have y ( q ) ( t n ) = y n ( q ) ( q = 0 , 1 , 2 , 3 , 4 ) . Based on Equations (18) and (21), we have formulated the following fourth-order nonlinear method:
y n + 1 = y n + 24 h y n ′ 4 24 y n ′ 3 − 12 h y n ′ 2 y n ″ + h 2 ( 6 y n ′ y n ″ 2 − 4 y n ′ 2 y n ″ ′ ) + h 3 ( 4 y n ′ y n ″ y n ″ ′ − 3 y n ′ ′ 3 − y n ′ 2 y n ( i v ) ) . ()

We use the notation “ N M A S 4 ” that stands for the above fourth-order nonlinear method with 𝒜 -stability.

The newly proposed formulation suggested in (2) can be expanded to obtain nonlinear methods with higher-order accuracy by putting m = 4 , 5 , ⋯ but it has been observed that the methods with m = 4 and its higher values do not yield 𝒜 − stable nonlinear methods. Therefore, we will be analyzing the nonlinear methods derived above with second-, third- and fourth-order of accuracy, that is, the methods given in (12), (17), and (22). Given below is the pseudo-code for the method given in (22). It will help readers to write the method in the programming language of their interest.

Algorithm . Pseudo code for the proposed nonlinear fourth-order method ( N M A S 4 ) given in (22) where the symbols f 1 ( t , y ) , f 2 ( t , y ) , f 3 ( t , y ) , and f 4 ( t , y ) stand for the first-, second-, third-, and fourth-order derivatives of y ( t )

cmm41213-gra-1000-b

3 Theoretical Analysis

This section is dedicated to theoretical analysis of proposed nonlinear methods wherein the analysis is carried out in terms of traditional and modern stability investigations, accuracy with consistency, and the principal local truncation error term.

3.1 Stability analysis

Linear absolute stability for the proposed nonlinear methods from orders 2 to 4 has been discussed in this subsection. Commonly, such investigation for stability requires taking a test problem called the Dahlquist's IVP35 as given below:
y ′ ( t ) = λ y ( t ) , R e ( λ ) < 0 . ()

Now, we carry out stability analysis of the proposed methods in the following theorem.

Theorem 2.The proposed nonlinear methods given in (12), (17), and (22) are 𝒜 -stable.

Proof.Following difference equations are obtained when the methods (12), (17), and (22) are employed on the Dahlquist's test problem (23):

NMAS 2 y n + 1 = y n [ 2 + h λ 2 − h λ ] , NMAS 3 , 4 y n + 1 = y n [ 12 + 6 h λ + h 2 λ 2 12 − 6 h λ + h 2 λ 2 ] . ()

Letting h λ = z , following stability functions are obtained:

NMAS 2 S ( z ) = 2 + z 2 − z , NMAS 3 , 4 S ( z ) = 12 + 6 z + z 2 12 − 6 z + z 2 , ()
for the methods (12), (17), and (22), respectively. A careful observation tells us that the stability functions NMAS 2 S ( z ) and NMAS 3 , 4 S ( z ) given above are the ( 1 , 1 ) and ( 2 , 2 ) Pade ' approximations to the exponential function exp ( z ) , respectively.36 Hence, this suggests 𝒜 -stability of the proposed methods given in (12), (17), and (22) whereas their absolute stability region is plotted in Figure 1 that contains the entire left half of the complex plane. The corresponding 3D graphics (3D stability surfaces) for the proposed third- and fourth-order methods are also shown in Figure 2A,B, respectively.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
The stability region (shaded) covers the whole left-half of the complex plane ℂ − for the proposed second-, third-, and fourth-order methods
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
(A) The graphic surface for the proposed second-order method (NMAS 2 ), and (B) the graphic surface for the proposed third-order (NMAS 3 ) and fourth-order (NMAS 4 ) methods

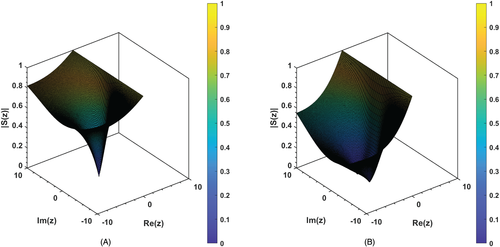
3.1.1 Stability via order stars

When it comes to relative measure for the stability of a nonlinear method, then order stars can be taken into account.37 Considerations concerning regions of absolute stability are an old concept for a method having a nonlinear structure. Nowadays, the concept has been taken over by the concept of order stars of a nonlinear function. One of the renowned works in Reference 38 introduced theoretical aspects of the order stars that are now considered to be the most powerful approach for the formulation and analysis of numerical schemes. An explanation of this relatively new concept can be found in Reference 39. As a start, let Z 1 and Z 2 be two complex-valued polynomials with index p and q, respectively, and the quotient be represented by S ( z ) = Z 1 Z 2 . It is easy to verify that the solution (zero) of the denominator Z 2 is said to be a pole for S ( z ) . Assume that the function G ( z ) be a complex function. An order star τ ( z ) defines a partition in the complex plane, namely the triplet { A + , A 0 , A − } , where each member of the triplet is defined as follows:
A + = { z : τ ( z ) > l } , A 0 = { z : τ ( z ) = l } , A − = { z : τ ( z ) < l } .
Principally, there exists two types (first and second) of order stars, τ ( z ) , usually taken as follows:
τ ( z ) = | S ( z ) G ( z ) | for l = 1 , or τ ( z ) = R e ( S ( z ) − G ( z ) ) for l = 0 .
Customarily, the first member of the triplet, namely A + requires to be shaded to distinguish it from the last member of the triplet ( A − ) . In this way, the region of growth of relative stability is associated with the set A + whereas, A − can be thought of as the region of contractivity. Finally, the second member A 0 of the triplet is considered as the boundary between two regions in the complex plane. At this stage, we are only concerned with the first type of order stars and the function G ( z ) = exp ( z ) . By redefining the order star of a nonlinear function S ( z ) , we obtain a set of the following three regions:
A + = { z ∈ ℂ : | S ( z ) | > | exp ( z ) | } = { z ∈ ℂ : | exp ( − z ) S ( z ) | > 1 } , A 0 = { z ∈ ℂ : | S ( z ) | = | exp ( z ) | } = { z ∈ ℂ : | exp ( − z ) S ( z ) | = 1 } , A − = { z ∈ ℂ : | S ( z ) | < | exp ( z ) | } = { z ∈ ℂ : | exp ( − z ) S ( z ) | < 1 } .

When plotted, the above sets produce star-like aspects which are somehow more anomalous than commonly known regions of absolute stability. Thus, at this stage, the concept of 𝒜 − acceptability can be defined.

Definition 2.( 𝒜 − acceptability) The stability function S ( z ) is said to be 𝒜 − acceptable if and only if A + has no intersection with the imaginary axis and it possesses no poles in the left half complex plane, namely where R e ( z ) < 0 .

In Figure 3, order stars are shown for the proposed method (12), whereas for the methods (17) and (22), the order stars are presented in Figure 4; where A + is represented by the shaded regions. From these figures, no intersection of A + is observed with the imaginary axis. In addition to this, there are no poles in the left-half of the complex plane R e ( z ) < 0 . This shows that the rational stability functions given in (25) are 𝒜 − acceptable with z = λ h , where R e ( z ) < 0 .

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Order stars of the N M A S 2 given in (12)
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Order stars of the N M A S 3 and N M A S 4 given in (17) and (22)

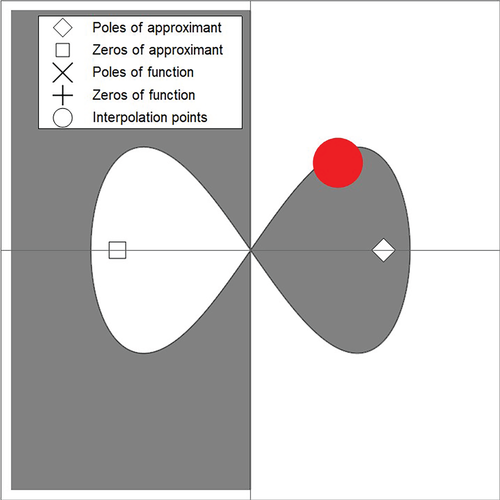
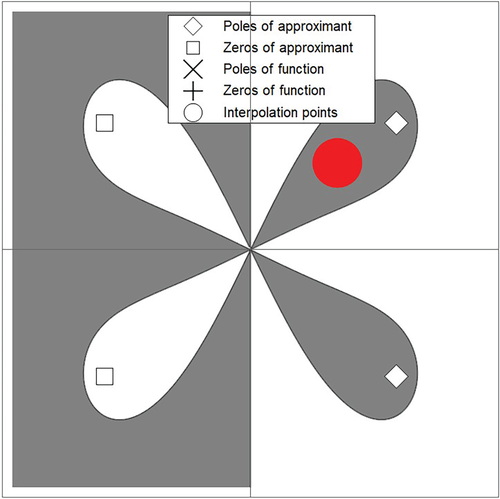
3.2 Order and consistency analysis

Consistency is one of the important characteristics of a numerical method. Being a condition on the numerical method itself, it requires approaching the underlying differential equation when the stepsize h → 0 . In this subsection, we aim to check consistency for the nonlinear methods devised in (12), (17), and (22). Subtracting y n from both sides of Equations (12), (17), and (22) and dividing the result by h, one leads to achieving the following identities:
y n + 1 − y n h = 2 y n ′ 2 2 y n ′ − h y n ″ , y n + 1 − y n h = 12 y n ′ 3 h 2 ( 3 y n ″ 2 − 2 y n ′ y n ″ ′ ) − 6 h y n ″ y n ′ + 12 y n ′ 2 , y n + 1 − y n h = 24 y n ′ 4 24 y n ′ 3 − 12 h y n ′ 2 y n ″ + h 2 ( 6 y n ′ y n ″ 2 − 4 y n ′ 2 y n ″ ′ ) + h 3 ( 4 y n ′ y n ″ y n ″ ′ − 3 y n ″ 3 − y n ′ 2 y n ( i v ) ) . ()
Applying limit as h tends to zero on both sides of each equation in (26), we have the following result:
lim h → 0 y n + 1 − y n h = y n ′ = f ( t n , y ( t n ) ) . ()

Thus, the newly proposed nonlinear methods (NMAS) given in (12), (17), and (22) are proved to be consistent with second-, third-, and fourth-order of accuracy.

3.3 Local truncation error analysis

To obtain the local truncation error for the family of proposed nonlinear methods NMAS, having an order of accuracy from two to four, a usual functional association with the methods has been considered as given below:
ℒ ( μ ( t ) , h ) = μ ( t n + h ) − y n + 1 , ()
where y n + 1 stands for any nonlinear method proposed in (12), (17), and (22).

Theorem 3.The nonlinear methods proposed in Equations (12), (17), and (22) have second-, third-, and fourth-order of accuracy, respectively.

Proof.The functional provided in (28) yields the following local truncation errors for the three nonlinear methods proposed:

L T E N M A S 2 = h 3 ( y ″ ′ ( t n ) 6 − y ″ ( t n ) 2 4 y ′ ( t n ) ) + 𝒪 ( h 4 ) , L T E N M A S 3 = h 4 ( y ( i v ) ( t n ) 24 + y ″ ( t n ) 3 8 y ′ ( t n ) 2 − y ″ ( t n ) y ″ ′ ( t n ) 6 y ′ ( t n ) ) + 𝒪 ( h 5 ) , L T E N M A S 4 = h 5 ( y ( v ) ( t n ) 120 − y ″ ( t n ) 4 16 y ′ ( t n ) 3 + y ″ ( t n ) 2 y ″ ′ ( t n ) 8 y ′ ( t n ) 2 − y ″ ( t n ) y ( i v ) ( t n ) 24 y ′ ( t n ) − y ″ ′ ( t n ) 2 36 y ′ ( t n ) ) + 𝒪 ( h 6 ) , ()
where y n ′ , y n ″ . y n ″ ′ , y n ( i v ) , and y n ( v ) show respectively the values to the first, second, third, fourth and fifth derivatives of y ( t ) at the point t n , provided that y n ′ ≠ 0 . It is clear from (29) that the proposed nonlinear methods in (12), (17), and (22) have second, third, and fourth-order of accuracy respectively, since the principal term in each equation of (29) consists of the term 𝒪 ( h q + 1 ) , where q denotes the order of the method.

It is also worth to be noted that the methods given in (7), (12), (17), and (22) will be exact when the solutions of the IVP given in (1) are considered in the following form:
y ( t ) = a + b t y ( t ) , y ( t ) = a + b t y ( t ) + c t , y ( t ) = a + b t y ( t ) + c t + d t 2 , y ( t ) = a + b t y ( t ) + c t + d t 2 + e t 3 , ()
respectively. The real constants a , b , c , d , and e have to be selected in such a way that neither the numerators nor the denominators in (30) vanish. With the elimination of some of the constants included in the following four systems that are obtained under each method (orders 1 to 4), one can obtain various ordinary differential equations for which the respective method produces the exact solution.
{ y ( t ) = a + b t y ( t ) , y ′ ( t ) = b y ( t ) b t + y 2 ( t ) } , { y ( t ) = a + b t y ( t ) + c t , y ′ ( t ) = b y ( t ) ( c t ) 2 + ( 2 c y ( t ) + b ) t + y 2 ( t ) } , { y ( t ) = a + b t y ( t ) + c t + d t 2 , y ′ ( t ) = − b ( d t 2 − y ) d 2 t 4 + 2 c d t 3 + ( c 2 + 2 d y ( t ) ) t 2 + ( 2 c y ( t ) + b ) t + y 2 ( t ) } , { y ( t ) = a + b t y ( t ) + c t + d t 2 + e t 3 , y ′ ( t ) = − b ( 2 e t 3 + d t 2 − y ( t ) ) e 2 t 6 + 2 d e t 5 + 2 c e t 4 + d 2 t 4 + 2 c d t 3 + 2 e t 3 y ( t ) + c 2 t 2 + 2 d t 2 y ( t ) + 2 c t y ( t ) + b t + y 2 ( t ) } . ()
For example, after eliminating conveniently different sets of parameters in the last system from (31), we get various differential equations for which the proposed fourth-order method is exact, as given below:
y ′ ( t ) = − ( 2 e t 3 + d t 2 − y ( t ) ) ( a − y ( t ) ) ( − e t 3 − d t 2 − c t + a − 2 y ( t ) ) t , y ′ ( t ) = − ( 2 e t 3 + d t 2 − y ( t ) ) ( a − y ( t ) ) 2 t ( b t + ( a − y ( t ) ) 2 ) , y ′ ( t ) = ( − e t 3 ( a − y ( t ) ) + ( a c − c y ( t ) + b ) t + 2 y ( t ) ( a − y ( t ) ) ) ( a − y ( t ) ) ( b t + ( a − y ( t ) ) 2 ) t , y ′ ( t ) = 2 ( a − y ( t ) ) ( d t 2 ( a − y ( t ) ) / 2 + ( a c − c y ( t ) + b ) t + 3 y ( t ) ( a − y ( t ) ) / 2 ) t ( b t + ( a − y ( t ) ) 2 ) .

4 Proposed Methods to Differential Systems

The nonlinear methods proposed in the present research work can also be applied to the first-order ordinary differential equations system under the component-wise approach. We consider a system of k ordinary differential equations in the vector form as follows:
y ′ = f ( t , y ) , y ( t 0 ) = y 0 , t 0 ≤ t ≤ t n ,
where
y ( t ) = ( y 1 ( t ) , y 2 ( t ) , … , y k ( t ) ) T , f ( t , y ( t ) ) = ( f 1 ( t , y 1 ( t ) , y 2 ( t ) , ⋯ , y k ( t ) ) , ⋯ , f k ( t , y 1 ( t ) , y 2 ( t ) , ⋯ , y k ( t ) ) T , y 0 = ( y 1 , 0 , . . . y k , 0 ) T . ()
For the case of a single ODE, the proposed nonlinear methods NMAS 2 , 3 , 4 of order two to four may be written as
y n + 1 = y n + h ϱ f ( t n , y n ; h ) ,
where ϱ f ( t n , y n ; h ) is commonly known as the incremental function, and the subscript f on the right-hand side shows that the dependence of ϱ f on its variables is through function f and possibly through derivatives of f. The incremental function ϱ f for each of the proposed methods can be respectively observed as follows:
ϱ f ( t n , y n ; h ) = 2 y n ′ 2 2 y n ′ − h y n ″ , ϱ f ( t n , y n ; h ) = 12 y n ′ 3 h 2 ( 3 y n ′ ′ 2 − 2 y n ′ y n ″ ′ ) − 6 h y n ″ y n ′ + 12 y n ′ 2 , ϱ f ( t n , y n ; h ) = 24 y n ′ 4 24 y n ′ 3 − 12 h y n ′ 2 y n ″ + h 2 ( 6 y n ′ y n ′ ′ 2 − 4 y n ′ 2 y n ″ ′ ) + h 3 ( 4 y n ′ y n ″ y n ″ ′ − 3 y n ′ ′ 3 − y n ′ 2 y n ( i v ) ) . ()
Implementing the proposed methods (12),(17), and (22) to each of the scalar equations in the differential system, we have obtained the result as:
y n + 1 = y n + h ϱ f ( t n , y n ; h ) ,
with
ϱ f ( t n , y n ; h ) = ( ϱ f 1 ( t n , y 1 , n , . . , y k , n ; h ) , ⋯ , ϱ f k ( t n , y 1 , n , … , y k , n ; h ) ) T ,
wherein each element function ϱ f k is easy to infer based on the expressions obtained in (33). Hence, the methods NMAS in equations (12),(17), and (22) are applicable to a system of ordinary differential equations.
When it comes to the stability of the proposed nonlinear methods for the system of differential equations, it is evident from available theory40 that the stability analysis of single-step methods (such as those proposed herein) used for systems can be discussed to the scalar model problem in (23). Hence, the proposed methods, from the classical viewpoint, are 𝒜 − stable for systems. This is true for linear multistep and Runge–Kutta (RK) methods but not true for nonlinear single-step methods. For instance, in the case of nonlinear single-step RK methods, a few authors41 have investigated the stability properties for a linear diagonal system with an arbitrary dimension k:
( y ′ = Λy , Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ k ) ) ,
which could be different for k = 1 (scalar case).
For all that, it is sufficient to consider the system to analyze stability behavior of the proposed nonlinear methods in (12),(17), and (22) for the system of first-order differential equations:42
y ′ = Λy , Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ k ) .
When we apply the proposed methods to the above equation, we obtain
y n + 1 = S y n , S = d i a g ( S 1 , S 2 , ⋯ , S k ) ,
where each component in S is a rational function as given in (25) respectively depends only on λ h i . Owing to this, the stability analysis can be kept under control for a scalar test equation. Consequently, the proposed methods in (12),(17), and (22), from the classical viewpoint, are 𝒜 − stable for systems. It is also worth mentioning at this stage that the multistep methods could be 𝒜 − stable for a scalar IVP but could be conditionally stable when it comes to solving systems of differential equations, unlike the nonlinear methods.

5 Variable Stepsize Approach

In the sections discussed above, constant stepsize approach was employed for the methods developed in (12),(17), and (22). However, it is known from the existing literature43 that a numerical method must behave accurately when stepsize h is varied. Keeping this observation in mind, we have attempted to test our developed methods under the variable stepsize approach. Now, the methods in (12),(17), and (22) can be joined with lower-order methods to perform as embedded pairs. It follows from such pairs that the numerical values utilized by lower-order methods are required to be used by higher-order methods, and this brings no additional computational cost for the method. The higher-order method is always employed to advance the integration steps once the lower-order method has been employed to estimate the local error at each step. The strategy proposed by Shampine et al.44 is adopted in the present study to design the nonlinear proposed methods under variable stepsize shape. At this stage, the procedure, as discussed in Reference 44, adopted for the variable stepsize approach is explained that depends on consideration of both the lower (p) and the higher ( p + 1 ) order methods. It may also be noted that we have considered Niekerk,45 Taylor,46 and Ramos47 methods with second-order accuracy as possible variable stepsize formulations for the Niekerk,48 Taylor,46 and the proposed methods with third-order accuracy respectively. Similarly, the Niekerk,48 Taylor,46 and Ramos49 methods with third-order accuracy are used as possible variable stepsize formulations for the Niekerk,48 Taylor,46 and the proposed methods with fourth-order accuracy respectively given in the present paper.

Let us consider that the local error l e n obtained at step n by the lower-order method is described below:
l e n = y ( t n + h ) − y n + 1 , ()
where y ( t ) stands for the theoretical solution. The following computable estimate comes out when the higher-order method is utilized to get y n + 1 :
e s t = y n + 1 ∗ − y n + 1 , = [ y ( t n + h ) − y n + 1 ] − [ y ( t n + h ) − y n + 1 ∗ ] , = l e n + 𝒪 ( h p + 2 ) . ()
It is easy to observe from the above results that l e n being the computable estimate for the local error of the lower order method is 𝒪 ( h p + 1 ) and thus dominates in (35) for suitably smaller values of h. Now, the error can be estimated by comparing less accurate solution y n + 1 with more accurate solution y n + 1 ∗ . However, one has to be wise enough to find a suitable pair of methods that share as many function evaluations as possible to make a local error estimation of some use. It is challenging to know how small the local error is at each integration step. Nonetheless, it has been shown in Reference 44 that such local error has to be smaller than the estimated local error. Generally, a local error tolerance t o l is prespecified to observe the size of the estimated error. If such an estimated error is larger than t o l , the current integration step is terminated, and a new attempt is made with a smaller stepsize. Given below is the discussion of the process for changing the stepsize. From (34), one obtains the following:
y ( t + h ) − y n + 1 = h p + 1 ϕ ( t n ) + 𝒪 ( h p + 2 ) . ()
If we take a step from t n with a new stepsize σ h , then the error would be
( σ h ) p + 1 ϕ ( t n ) + 𝒪 ( ( σ h ) p + 2 ) = σ p + 1 h p + 1 ϕ ( t n ) + 𝒪 ( h p + 2 ) , = σ p + 1 e s t + 𝒪 ( h p + 2 ) . ()
The largest stepsize that we predict will pass the error test corresponds to choosing σ so that
| σ p + 1 e s t | ≈ t o l .
Then the new stepsize is given by
h ( t o l | e s t | ) 1 / ( p + 1 ) . ()
A safety factor denoted by φ comes into play within Equation (38) on the recommendation of various researchers as given below:
h n e w = h φ ( t o l | e s t | ) 1 / ( p + 1 ) , ()
where φ is considered to be a suitable adjustment factor φ ≈ 0 . 9 .50 It is worth noting that the only purpose for taking φ is to avoid the failed integration steps, whereas φ ∈ ( 0 , 1 ) and p shows the order of the lower order method. The new stepsize h new has to be confined within the interval [ h min , h max ] in order to avoid the large possible fluctuations in it. Note that h min and h max denote the allowed minimum and maximum stepsize values, respectively. When ‖ e s t ‖ < t o l (successful step) is achieved, the above approach will be used at the successive rate to predict the stepsize for the upcoming integration step. Moreover, we do not need to worry about the selection of the initial stepsize (see References 51 and 52) because the method is structured in a way that it will correct this value (in case if a smaller value is selected53) automatically under the variable stepsize approach.

6 Numerical Dynamics with Results and Discussion

In this section, we have simulated several models, including nonlinear, stiff, and singular IVPs. Results obtained with the proposed second-, third-, and fourth-order convergent methods are shown in tabular form, whereas these results have been compared with the results obtained with second-order methods called the nonstandard explicit integration scheme (Ramos 2 ) taken from Reference 47 and the Taylor series method given as y n + 1 = y n + h y n ′ + h 2 2 y n ″ , third-order methods called the rational one-step method (Niekerk 3 ) taken from Reference 48 and the Taylor series method given as y n + 1 = y n + h y n ′ + h 2 2 y n ″ + h 3 6 y n ″ ′ ; and finally with the fourth-order methods known as the rational one-step method (Niekerk 4 ) taken from Reference 48 and the Taylor series method given as y n + 1 = y n + h y n ′ + h 2 2 y n ″ + h 3 6 y n ″ ′ + h 4 24 y n ( i v ) . The comparison of results is based on three types of absolute errors known as the maximum absolute error computed by max t ∈ [ 0 , T ] | y ( t n ) − y n | , the final absolute error computed by | y ( t T ) − y T | , the absolute root mean squared value computed by 1 n ∑ i | y ( t i ) − y i | 2 , and the CPU time is measured in seconds. All the numerical computations have been performed using MATLAB with version “9.8.0.1323502 (R2020a)” running on OS Windows with a processor Intel(R) Core(TM) i7-1065G7 CPU @ 1.30 GHz 1.50 GHz and installed RAM of 24.0 GB. During several simulations, the time value obtained through MATLAB on first run of the code is zero, which means that the code takes less time than the time unit used (1/100000 s.) to do the computations.

Problem 1.Consider the following nonlinear model for the kinetic behavior of biosorption:14

κ y ′ ( t ) = y ( t ) − y ( t ) 3 , y ( 0 ) = 1 / 10 , 0 ≤ t ≤ 1 . 0 , ()
with exact solution y ( t ) = 1 99 exp ( − 2 t / κ ) + 1 , where κ = 1 0 − 1 .

For the nonlinear model 1, we have shown the numerical results in Tables 1,2, and 3 with second-, third-, and fourth-order methods, respectively. It can be observed from these tables that the proposed nonlinear family of methods not only yields the smallest errors but also takes the fewest amount of CPU time (s) in most cases. It is also evident from the Tables that the second-order explicit nonstandard method (Ramos 2 ) produces results as promising as the results obtained with the second-order proposed nonlinear method. Moreover, it is also worth to be noted that the errors decrease under each method, with particularly third- and fourth-order convergence for smaller values of the stepsize h.

TABLE 1. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each second-order method with constant stepsize for Problem 1
Method/h 1 / 100 1 / 200 1 / 400 1 / 800 1 / 1600
Ramos 2 1.2126e-03 3.0469e-04 7.6400e-05 1.9129e-05 4.7862e-06
5.7341e-09 1.4600e-09 3.6676e-10 9.1813e-11 2.2963e-11
4.5575e-04 1.1472e-04 2.8790e-05 7.2119e-06 1.8048e-06
1.8360e-04 2.8900e-04 7.2650e-04 1.3643e-03 2.6860e-03
Taylor 2 3.2945e-04 8.3120e-05 2.0878e-05 5.2338e-06 1.3101e-06
1.0615e-08 2.3748e-09 5.6744e-10 1.3900e-10 3.4417e-11
1.2693e-04 3.1626e-05 7.8987e-06 1.9740e-06 4.9344e-07
1.8360e-04 3.0620e-04 7.2650e-04 1.3491e-03 2.6860e-03
N M A S 2 1.2126e-03 3.0469e-04 7.6400e-05 1.9129e-05 4.7862e-06
5.7341e-09 1.4600e-09 3.6676e-10 9.1813e-11 2.2963e-11
4.5575e-04 1.1472e-04 2.8790e-05 7.2119e-06 1.8048e-06
1.6490e-04 2.8900e-04 7.4230e-04 1.3643e-03 2.5188e-03
TABLE 2. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each second-order method with constant stepsize for Problem 1
Method/h 1 / 100 1 / 200 1 / 400 1 / 800 1 / 1600
Niekerk 3 1.3385e-04 2.1345e-05 2.8790e-06 3.8033e-07 4.9007e-08
2.7776e-10 1.9457e-11 2.4588e-12 3.1841e-13 4.2411e-14
4.2443e-05 3.1035e-06 3.6557e-07 4.1214e-08 4.3838e-09
4.8110e-04 5.9510e-04 1.1226e-03 3.3188e-03 2.7823e-03
Taylor 3 2.7499e-05 3.5297e-06 4.4640e-07 5.6146e-08 7.0403e-09
4.7270e-10 5.4869e-11 6.6053e-12 8.1046e-13 1.0025e-13
7.4220e-06 9.4883e-07 1.2011e-07 1.5115e-08 1.8958e-09
4.5670e-04 5.5960e-04 8.4510e-04 1.8447e-03 2.7529e-03
N M A S 3 1.5565e-05 1.9864e-06 2.5104e-07 3.1545e-08 3.9538e-09
8.8755e-12 1.3355e-12 1.8119e-13 2.3537e-14 2.8866e-15
5.2602e-06 6.7436e-07 8.5385e-08 1.0742e-08 1.3472e-09
3.2130e-04 5.1470e-04 8.0700e-04 1.2403e-03 2.1836e-03
TABLE 3. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each second-order method with constant stepsize for Problem 1
Method/h 1 / 100 1 / 200 1 / 400 1 / 800 1 / 1600
Niekerk 4 5.8544e-07 3.6957e-08 2.3184e-09 1.4521e-10 9.0847e-12
3.8390e-12 2.3959e-13 1.4877e-14 9.9920e-16 2.2204e-16
1.9751e-07 1.2474e-08 7.8398e-10 4.9139e-11 3.0758e-12
2.7240e-04 4.8340e-04 1.2256e-03 2.4422e-03 3.1887e-03
Taylor 4 1.0231e-06 6.5428e-08 4.1438e-09 2.6065e-10 1.6343e-11
1.7014e-11 9.7944e-13 5.8731e-14 3.9968e-15 0.0000e+00
2.9736e-07 1.8831e-08 1.1865e-09 7.4477e-11 4.6653e-12
2.4270e-04 4.0790e-04 9.9530e-04 1.6764e-03 4.1680e-03
N M A S 4 4.0982e-07 2.5858e-08 1.6248e-09 1.0183e-10 6.3731e-12
3.6751e-12 2.2926e-13 1.4322e-14 9.9920e-16 2.2204e-16
1.3402e-07 8.4866e-09 5.3409e-10 3.3499e-11 2.0973e-12
2.7310e-04 4.7410e-04 8.6720e-04 1.8285e-03 3.6483e-03

Problem 2.Consider the following singular IVP:47

y ′ ( t ) = 1 + y 2 ( t ) , y ( 0 ) = 1 , 0 ≤ t ≤ 1 . 0 , ()
with the exact solution y ( t ) = t a n ( t + π / 4 ) having singularity at t = π / 4 .

For the singular IVP 2, we have shown the numerical results in the Tables 4,5, and 6 with second-, third-, and fourth-order methods, respectively. It can be observed from these tables that the proposed nonlinear family of methods not only yields the smallest errors but also takes the fewest amount of CPU time (s). It is also evident from Tables 4,5, and 6 that Taylor's second-, third-, and fourth-order methods failed at various iterations, and the second-order explicit nonstandard method (Ramos 2 ) produces results as promising as the results obtained with the second-order proposed nonlinear method. Moreover, it is also worthy of being noted in Table 6 that the numerical results obtained under fourth-order Niekerk and the proposed method with fourth-order convergence are identical as long as h = 1 . 25 e − 2 . However, it is seen that the errors decrease with the proposed method ( N M A S 4 ) for h = 6 . 25 e − 3 and smaller values of the stepsize h.

TABLE 4. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each second-order method with constant stepsize for Problem 2
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Ramos 2 1.5191e+01 3.2714e+00 1.4700e+00 9.4682e+00 2.3324e+00
7.4191e-02 1.8418e-02 4.5964e-03 1.1486e-03 2.8712e-04
4.5818e+00 7.2320e-01 2.6218e-01 1.0531e+00 1.9019e-01
2.5172e-03 4.5310e-04 2.4541e-03 1.0980e-04 1.4560e-04
Taylor 2 4.4564e+04 Failed at t = 0 . 7 Failed at t = 9 . 5 e − 1 Failed at t = 8 . 75 e − 1 Failed at t = 8 . 25 e − 1
4.4564e+04
1.3437e+04
4.4522e-03
N M A S 2 1.5191e+01 3.2714e+00 1.4700e+00 9.4682e+00 2.3324e+00
7.4191e-02 1.8418e-02 4.5964e-03 1.1486e-03 2.8712e-04
4.5818e+00 7.2320e-01 2.6218e-01 1.0531e+00 1.9019e-01
2.5172e-03 4.5310e-04 2.4541e-03 1.0980e-04 1.4560e-04
TABLE 5. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each third-order method with constant stepsize for Problem 2
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Niekerk 3 2.0259e-01 2.3951e-02 5.7313e-03 1.7280e-02 2.1441e-03
9.1369e-04 1.0652e-04 1.2843e-05 1.5763e-06 1.9523e-07
6.1119e-02 5.3116e-03 1.0094e-03 1.9222e-03 1.7500e-04
2.0280e-04 3.5780e-04 3.7050e-04 3.8430e-04 4.2710e-04
Taylor 3 2.6337e+11 Failed at t = 0 . 75 Failed at t = 0 . 9 Failed at t = 0 . 85 Failed at t = 8 . 1875 e − 01
2.6337e+11
7.9409e+10
3.8745e-03
N M A S 3 8.3198e-03 5.2086e-04 6.2214e-05 9.6708e-05 6.0445e-06
4.8884e-05 3.0607e-06 1.9138e-07 1.1962e-08 7.4768e-10
2.5098e-03 1.1533e-04 1.1030e-05 1.0757e-05 4.9312e-07
7.5300e-05 1.3740e-04 1.5950e-04 1.5630e-04 7.6900e-05
TABLE 6. Maximum absolute errors on [ 0 , 1 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 1 . 0 ] (third row), and CPU time in seconds (fourth row) of each fourth-order method with constant stepsize for Problem 2
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Niekerk 4 8.3198e-03 5.2086e-04 6.2214e-05 9.6706e-05 6.1823e-06
4.8884e-05 3.0606e-06 1.9138e-07 1.2175e-08 1.1309e-09
2.5098e-03 1.1533e-04 1.1030e-05 1.0757e-05 5.0543e-07
6.1972e-03 2.5592e-03 1.9988e-03 6.1820e-03 5.8807e-03
Taylor 4 1.0604e+22 Failed at t = 0 . 75 Failed at t = 0 . 9 Failed at t = 8 . 375 e − 1 Failed at t = 8 . 1250 e − 1
1.0604e+22
3.1973e+21
4.3795e-03
N M A S 4 8.3198e-03 5.2086e-04 6.2214e-05 9.6708e-05 6.0445e-06
4.8884e-05 3.0607e-06 1.9138e-07 1.1962e-08 7.4768e-10
2.5098e-03 1.1533e-04 1.1030e-05 1.0757e-05 4.9312e-07
2.2930e-04 2.4120e-04 2.0140e-04 4.2750e-04 4.7880e-04

Problem 3.Consider the following nonlinear IVP for the Logistic growth:54

y ′ ( t ) = y ( t ) 4 ( 1 − y ( t ) 20 ) , y ( 0 ) = 1 , 0 ≤ t ≤ 2 . 0 , ()
with exact solution y ( t ) = 20 1 + 19 exp ( − t 4 ) .

During the numerical solution of the nonlinear logistic growth model 3, it is observed once again that the proposed family surpasses the other methods (with the exception of Ramos 2 ) as shown in Tables 7–9 with computation of different errors and CPU time (s). For the nonlinear IVP above, third-order Taylor and Niekerk methods compete well with the proposed methods. However, the latter still maintains the smallest errors and simultaneously uses the smallest amount of CPU time. Moreover, it is also worthy of being noted in Table 9 wherein numerical results obtained under fourth-order Niekerk and proposed are identical, and this happens because the IVP under consideration is not singular, for which the proposed method ( N M A S 4 ) is always seen to be outperforming Niekerk 4 .

TABLE 7. Maximum absolute errors on [ 0 , 2 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 2 . 0 ] (third row), and CPU time in seconds (fourth row) of each second-order method with constant stepsize for Problem 3
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Ramos 2 3.8270e-05 9.5668e-06 2.3916e-06 5.9791e-07 1.4948e-07
3.8270e-05 9.5668e-06 2.3916e-06 5.9791e-07 1.4948e-07
2.0403e-05 5.0490e-06 1.2558e-06 3.1313e-07 7.8180e-08
1.0160e-04 1.1590e-04 1.3532e-03 1.2258e-03 1.0752e-03
Taylor 2 4.8470e-05 1.2199e-05 3.0599e-06 7.6625e-07 1.9172e-07
4.8470e-05 1.2199e-05 3.0599e-06 7.6625e-07 1.9172e-07
2.6477e-05 6.6051e-06 1.6494e-06 4.1212e-07 1.0300e-07
2.3980e-04 2.7460e-04 1.4837e-03 1.7237e-03 1.0954e-03
N M A S 2 3.8270e-05 9.5668e-06 2.3916e-06 5.9791e-07 1.4948e-07
3.8270e-05 9.5668e-06 2.3916e-06 5.9791e-07 1.4948e-07
2.0403e-05 5.0490e-06 1.2558e-06 3.1313e-07 7.8180e-08
1.0160e-04 1.1590e-04 1.3532e-03 1.2258e-03 1.0752e-03
TABLE 8. Maximum absolute errors on [ 0 , 2 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 2 . 0 ] (third row), and CPU time in seconds (fourth row) of each third-order method with constant stepsize for Problem 3
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Niekerk 3 1.8128e-07 2.2758e-08 2.8509e-09 3.5674e-10 4.4617e-11
1.8128e-07 2.2758e-08 2.8509e-09 3.5674e-10 4.4617e-11
9.5980e-08 1.1923e-08 1.4857e-09 1.8541e-10 2.3157e-11
2.0420e-04 2.4790e-04 2.2840e-04 3.4440e-04 4.9790e-04
Taylor 3 1.1906e-07 1.4886e-08 1.8610e-09 2.3263e-10 2.9076e-11
1.1906e-07 1.4886e-08 1.8610e-09 2.3263e-10 2.9076e-11
7.1051e-08 8.8475e-09 1.1038e-09 1.3784e-10 1.7219e-11
7.3300e-05 1.2200e-04 2.9160e-04 4.2530e-04 4.3360e-04
N M A S 3 3.9862e-10 2.4913e-11 1.5565e-12 9.7922e-14 3.1086e-15
3.9862e-10 2.4913e-11 1.5565e-12 9.7922e-14 3.1086e-15
2.1252e-10 1.3148e-11 8.1731e-13 5.1111e-14 1.5452e-15
7.1200e-05 1.1620e-04 1.5460e-04 1.3540e-04 3.4460e-04
TABLE 9. Maximum absolute errors on [ 0 , 2 . 0 ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 2 . 0 ] (third row), and CPU time in seconds (fourth row) of each fourth-order method with constant stepsize for Problem 3
Method/h 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2 6 . 25 e − 3
Niekerk 4 3.9862e-10 2.4913e-11 1.5568e-12 9.7922e-14 3.1086e-15
3.9862e-10 2.4913e-11 1.5568e-12 9.7922e-14 3.1086e-15
2.1252e-10 1.3148e-11 8.1734e-13 5.1111e-14 1.5452e-15
2.4610e-04 2.2560e-04 2.9140e-04 4.9450e-04 1.2952e-03
Taylor 4 8.2151e-10 5.2305e-11 3.3002e-12 2.0894e-13 1.7764e-14
8.2151e-10 5.2305e-11 3.3002e-12 2.0894e-13 1.7542e-14
3.8996e-10 2.4454e-11 1.5308e-12 9.6259e-14 8.7814e-15
1.0750e-04 5.8740e-04 6.6960e-04 6.4600e-04 1.7980e-03
N M A S 4 3.9862e-10 2.4912e-11 1.5565e-12 9.7922e-14 3.1086e-15
3.9862e-10 2.4912e-11 1.5565e-12 9.7922e-14 3.1086e-15
2.1252e-10 1.3148e-11 8.1731e-13 5.1111e-14 1.5452e-15
1.0370e-04 1.4810e-04 2.5360e-04 3.0590e-04 1.1259e-03

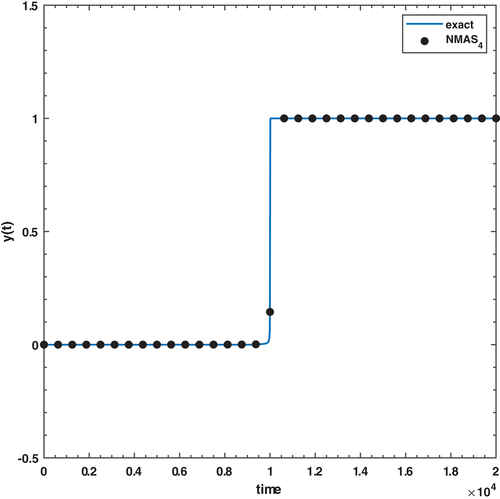
Problem 4.Consider the following stiff IVP for the flame propagation:55

y ′ ( t ) = y 2 ( t ) − y 3 ( t ) , y ( 0 ) = ϵ , 0 ≤ t ≤ 2 / ϵ , ()
with exact solution y ( t ) = 1 L a m b e r t W ( ( 9999 exp ( − t + 9999 ) ) ) + 1 , where L a m b e r t W − is a special function named after Johann Heinrich Lambert—a Swiss polymath.

For the numerical experiment 4, we have considered an interesting model (43) of flame propagation which is a stiff ordinary differential equation as described in Reference 55. The situation illustrates that when a match is lighted, then the ball of the flame overgrows until it reaches a critical size. After that, the ball remains critical because the amount of oxygen consumed by the combustion inside the ball balances the amount of oxygen available through the surface. In model 4, the variable y ( t ) shows the radius of the ball, whereas the terms y 2 ( t ) and y 3 ( t ) stand for the surface area and the volume, respectively, at any time t. Since the initial radius, ϵ of the ball could be very small. It later varies with time. Upon comparison in Tables 10–11, the proposed third-order method ( N M A S 3 ) performs almost equally well as the two other third-order methods, whereas Niekerk 3 fails when h = 2 e − 1 . The numerical simulations obtained with the fourth-order version of the proposed nonlinear method ( N M A S 4 ) are identical to the fourth-order Niekerk and Taylor results. However, the method N M A S 4 still consumes fewer CPU seconds in most of the cases. The initial radius ϵ of the ball is taken to be 1 0 − 4 during simulations. Figure 5 represents a compelling visualization of the stiff behavior of the flame propagation model that is well captured by the proposed method ( N M A S 4 ). It shows that the proposed methods are adequate while dealing with the stiff models used in real-life applications.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Stiff behavior under the proposed method ( N M A S 4 ) with ϵ = 1 0 − 4 and stepsize h = 1 . 25 e − 02 for the model of flame propagation given by Equation (43)
TABLE 10. Maximum absolute errors on [ 0 , 2 / ϵ ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 2 / ϵ ] (third row), and CPU time in seconds (fourth row) of each third-order method with constant stepsize for Problem 4
Method/h 2 e − 1 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2
Niekerk 3 Failed at t = 10044 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
5.5511e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
1.1144e-01 2.3943e-01 5.4002e-01 9.0758e-01
Taylor 3 1.4199e-03 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
2.2204e-16 4.4409e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5702e-04 2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
7.7905e-02 1.3910e-01 2.7971e-01 5.7552e-01 1.1061e+00
N M A S 3 1.4199e-03 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
2.2204e-16 5.5511e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5702e-04 2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
8.4652e-02 1.3794e-01 2.7824e-01 5.7156e-01 1.1114e+00
TABLE 11. Maximum absolute errors on [ 0 , 2 / ϵ ] (first row), final absolute errors (second row), root mean squared errors on [ 0 , 2 / ϵ ] (third row), and CPU time in seconds (fourth row) of each third-order method with constant stepsize for Problem 4
Method/h 2 e − 1 1 e − 1 5 e − 2 2 . 5 e − 2 1 . 25 e − 2
Niekerk 4 1.4199e-03 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
2.2204e-16 5.5511e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5702e-04 2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
3.9560e-04 3.2040e-04 3.3960e-03 4.3142e-03 3.8104e-03
Taylor 4 1.4199e-03 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
2.2204e-16 5.5511e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5702e-04 2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
9.2730e-04 9.6140e-04 3.1824e-03 2.3384e-03 6.4178e-03
N M A S 4 1.4199e-03 1.4199e-03 1.4199e-03 1.4200e-03 1.4200e-03
2.2204e-16 5.5511e-16 1.1102e-15 2.2204e-15 4.4409e-15
2.5702e-04 2.5701e-04 2.5700e-04 2.5700e-04 2.5700e-04
2.0037e-03 3.5420e-04 1.6781e-03 4.0011e-03 2.6005e-03

Problem 5.Consider the following second-order IVP:49

( 2 t + 3 ) y ″ ( t ) + 4 y ′ ( t ) = 0 , y ( 0 ) = 1 , y ′ ( 0 ) = 1 , 0 ≤ t ≤ 1 . 0 . ()

Given below is the system of two first-order IVPs equivalent to the above second-order equation:
y 1 ′ ( t ) = y 2 ( t ) , y 1 ( 0 ) = 1 , y 2 ′ ( t ) = − 4 y 2 ( t ) 2 t + 3 , y 2 ( 0 ) = 1 . ()
Exact solution is as follows:
y 1 ( t ) = 5 2 − 9 4 ( t + 3 / 2 ) , y 2 ( t ) = 9 4 ( t + 3 / 2 ) 2 . ()

For numerical Problem 5, we have taken a second-order IVP, or equivalently a system of two first-order differential equations wherein the singularity occurs at t = − 3 / 2 . This singular system has been integrated over the integration interval [ 0 , 1 ] while using the variable stepsize approach to compute the number of steps, maximum absolute error in both state variables, and the amount of time consumed by third- and fourth-order Niekerk and proposed nonlinear family of methods with variation in the tolerance values tol ∈ { 1 0 − 3 , 1 0 − 6 , 1 0 − 9 , 1 0 − 12 } . It is to be noted that second-order methods are not used herein as we could not find an authentic first-order nonlinear method to be used as an embedded type pair to utilize the variable stepsize approach. It is evident from Table 12 that each third-order method yields an almost equivalent amount of maximum absolute errors. However, the Niekerk and proposed methods consume fewer steps with comparably similar consumption of CPU time (s). As far as Table 13 is concerned, the Niekerk third-order could not be successful in producing a reasonable number of steps and hence was not considered. On the other hand, the proposed nonlinear method with fourth-order convergence performs far better than its Taylor counterpart with minimum CPU time.

TABLE 12. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) of each third-order method with variable stepsize for Problem 5
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Niekerk 3 7 41 385 3821
5.8246e-05 9.0574e-08 9.6490e-11 9.7922e-14
1.0362e-04 1.4591e-07 1.5460e-10 1.5582e-13
0 0 1.5625e-02 1.5625e-01
Taylor 3 11 80 767 7640
3.0947e-05 3.4275e-08 3.4679e-11 4.0856e-14
2.1424e-04 2.8090e-07 2.9043e-10 2.9021e-13
0 0 3.1250e-02 2.9688e-01
N M A S 3 7 41 385 3821
4.3114e-05 6.7921e-08 7.2367e-11 7.0388e-14
7.7261e-05 1.0947e-07 1.1596e-10 1.1702e-13
0 0 3.1250e-02 1.8750e-01
TABLE 13. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) under fourth-order Taylor and proposed methods with variable stepsize for Problem 5
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Taylor 4 9 29 139  754
1.7932e-5 9.9999e-06 9.9999e-6 9.9999e-06
1.3766e-04 1.3333e-05 1.3333e-05 1.3333e-05
0 0 0 3.125e-02
N M A S 4 10 20 76 389
1.7685e-05 3.7172e-08 4.6542e-11 5.0626e-14
3.3606e-05 6.2251e-08 7.5484e-11 7.7827e-14
0 0 0 1.5625e-02

Problem 6.Consider the following nonlinear stiff system:56

y 1 ′ ( t ) = − 200 y 2 2 ( t ) , y 1 ( 0 ) = 1 , y 2 ′ ( t ) = − 100 y 2 ( t ) y 2 ( 0 ) = 1 , ()
with exact solution y 1 ( t ) = exp ( − 200 t ) , y 2 ( t ) = exp ( − 100 t ) and   0 ≤ t ≤ 1 . 0 .

For the numerical experiment 6, a nonlinear stiff system is chosen to test the methods. The numerical results are shown in the Tables 14 and 15 reveal the tolerance values of 1 0 − 3 and 1 0 − 6 are enough to obtain acceptable absolute maximum errors with the smallest number of steps in most of the cases under the third and fourth-order proposed methods.

TABLE 14. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) for each third-order method with variable stepsize for Problem 6
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Niekerk 3 41 250 2328 23122
8.0787e-03 8.8823e-05 8.9994e-07 9.0108e-09
6.3586e-04 8.0051e-07 7.9479e-10 6.8512e-13
0 0 7.8125e-02 1.4843
T a y l o r 3 58 224 1875 18384
2.2416e-02 2.3796e-04 2.4026e-06 2.4069e-08
4.8170e-04 4.6086e-07 4.8694e-10 4.8312e-13
0 0 4.6875e-02 9.6875e-01
N M A S 3 30 239 2319 23113
6.7037e-03 8.7092e-05 8.9816e-07 9.0090e-09
7.5574e-06 7.5648e-09 7.5981e-12 7.4852e-15
0 1.5625e-02 7.8125e-02 1.5938
TABLE 15. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) for each fourth-order method with variable stepsize for Problem 6
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Niekerk 4 18 73 383 2123
9.3665e-02 2.8873e-03 9.0145e-05 2.8438e-06
6.2814e-4 4.76e-06 2.8052e-08 1.5904e-10
1.5625e-02 0 1.5625e-02 9.3750-02
T a y l o r 4 47 83 289 1448
9.5727e-02 3.4292e-03 1.1480e-04 3.6740e-06
3.5884e-03 1.8307e-05 1.1419e-07 6.5519e-10
0 0 1.5625e-02 4.6875e-02
N M A S 4 23 74 385 2125
4.1046e-02 2.8806e-03 9.0511e-05 2.8532e-06
3.8977e-04 4.8655e-06 2.8183e-08 1.5929e-10
0 0 1.5625e-02 9.3750e-02

Problem 7.Consider the following second-order mildly stiff nonhomogeneous IVP:57

y ″ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 2 exp ( − 3 t ) , y ( 0 ) = 1 , y ′ ( 0 ) = − 2 , 0 ≤ t ≤ 5 . ()

Given below is the system of two first-order IVPs equivalent to the above second-order equation:
y 1 ′ ( t ) = y 2 ( t ) , y 1 ( 0 ) = 1 , y 2 ′ ( t ) = − 2 y 1 ( t ) − 3 y 2 ( t ) + 2 exp ( − 3 t ) , y 2 ( 0 ) = − 2 . ()
Exact solution is as follows:
y 1 ( t ) = exp ( − t ) − exp ( − 2 t ) + exp ( − 3 t ) , y 2 ( t ) = 2 exp ( − 2 t ) − exp ( − t ) − 3 exp ( − 3 t ) . ()

For the numerical Problem 7, it is evident from Tables 16 and 17 that the third- and fourth-order proposed nonlinear methods perform better than the rest of the methods while consuming the same number of steps as in the Niekerk's methods but with smallest errors and comparable CPU time (s). It is worth to be noted that the fourth-order Taylor method could not compete with either method, leaving the proposed family to be the best among others taken for comparison as can be observed in Table 17.

TABLE 16. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) for each third-order method with variable stepsize for Problem 7
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Niekerk 3 23 188 1833 18284
2.6046e-04 3.8680e-07 4.0732e-10 4.1023e-13
2.3191e-04 4.6983e-07 5.0416e-10 5.0726e-13
0 1.5625e-02 7.8125e-02 1.4531
T a y l o r 3 31 254 2478 24712
1.1288e-04 1.4821e-07 1.5480e-10 1.5553e-13
1.8117e-04 2.2914e-07 2.4365e-10 2.4522e-13
0 1.5625e-02 9.375e-02 2.1875
N M A S 3 23 188 1833 18284
2.2813e-04 3.5144e-07 3.7229e-10 3.7420e-13
2.3372e-04 4.4405e-07 4.7339e-10 4.7640e-13
0 0 9.375e-02 1.5781
TABLE 17. No. of steps (first row), maximum absolute error in y 1 ( t ) (second row), maximum absolute error in y 2 ( t ) (third row), and CPU time in seconds (fourth row) for each four order method with variable stepsize for Problem 7
Method/tol 1 0 − 3 1 0 − 6 1 0 − 9 1 0 − 12
Niekerk 4 18 68 346 1910
2.6112e-04 3.6537e-07 1.2425e-09 1.0432e-12
4.8810e-04 5.8438e-07 1.3439e-09 1.0264e-12
0 0 3.125e-02 1.2500e-1
T a y l o r 4 22 85 439 2425
6.0898e-05 3.9998e-05 3.9998e-05 3.9998e-05
1.1999e-04 1.1999e-04 1.1999e-04 1.1999e-04
0 0 1.5625e-02 1.0938e-01
N M A S 4 18 68 346 1910
5.9563e-05 1.2362e-07 1.5878e-10 1.6766e-13
1.2534e-04 2.1919e-07 2.6953e-10 2.8128e-13
0 0 3.125e-02 1.2500e-01

7 Concluding Remarks

A new family of nonlinear numerical methods proposed in the present research study is proved to be suitable for dealing with nonlinear, stiff, and singular differential equations' based models. Three members of the proposed family having an order of convergence 2 , 3 , and 4 are shown to be both 𝒜 − stable and 𝒜 − acceptable. Consistency and order of convergence with analysis of local truncation errors are well established, wherein the methods are equally applicable for systems of ordinary differential equations. The variable stepsize approach is used for nonlinear, stiff, and singular systems to obtain the smallest absolute errors with the proposed family. Real-life applications, including nonlinear logistic growth and stiff models describing the dynamical behavior of flame propagation, are successfully dealt with by the methods proposed. It would be interesting to devise, in future studies, a new class of numerical methods with multiple steps and an ℒ − stability feature.

Notations

  • h
  • Stepsize
  • tol
  • Tolerance
  • A− stability
  • Absolute stability
  • hini
  • Initial stepsize
  • RMS
  • Root mean squared error
  • LMZS1
  • First-order linear method with zero-stability
  • NMAS2
  • Numerical method with A − acceptability having second-order accuracy
  • NMAS3
  • Numerical method with A − acceptability having third-order accuracy
  • NMAS4
  • Numerical method with A − acceptability having fourth-order accuracy
  • Ramos2
  • Explicit nonstandard second order method
  • LTE
  • Local truncation error
  • est
  • Estimate error
  • len
  • Local error

    • ACKNOWLEDGMENTS

    The first and second authors are grateful to Mehran University of Engineering and Technology, Jamshoro, Pakistan, for the kind support and facilities to carry out this research work. The first author is also grateful to the Department of Mathematics, Near East University, Cyprus, including the third author.

      Author Contributions

      Sania Qureshi: Conceived of the idea, derived the proposed nonlinear methods, and performed numerical simulations. Amanullah Soomro: Carried out theoretical analysis of each proposed method. Evren Hınçal: Carried out supervision of the entire work. All author equally contributed toward writing and finalizing the article.

      Biographies

      • Dr. Sania Qureshi was born in Hyderabad in 1982. S. Qureshi completed her PhD in 2019 from University of Sindh. During PhD, she was awarded two scholarships under which she visited Division of Mathematics, University of Dundee, Scotland, UK in 2016 and Institute of Computational Mathematics, Technische Universitaet Braunschweig, Germany in 2018. She has several publications on mathematical epidemiology, fractional calculus, and numerical techniques for ODEs. Since 2008, she is the full-time faculty member at Mehran University of Engineering and Technology, Pakistan.

      • Mr. Amanullah Soomro was born in Umerkot in 1995. In 2019, A. Soomro graduated from Institute of Mathematics and Computer Sciences, University of Sindh, Jamshoro with BS degree. Nowadays, he is pursuing M.Phil research studies from the department of Basic Sciences and Related Studies at Mehran University of Engineering and Technology, Jamshoro, Sindh, Pakistan. He is the co-author of two research papers recently published in Scopus international journals. At the same time, A. Soomro is serving as a Teaching Assistant in the same department.

      • Prof. Dr. Evren Hınçal was born in Lefkoşa in 1973. In 1991, E. Hınçal completed his PhD at the Eastern Mediterranean University with the cooperation of Imperial College. Between the years 2000 and 2001 E. Hınçal visited Imperial College and he worked with Neurobiology Group on the cancer epidemiology. E. Hınçal has several publications about cancer statistics, cancer epidemiology and mathematical modeling about cancer in refereed international journals. Since 2007, he is the full-time member of Near East University Department of Mathematics.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.