RESEARCH ARTICLE

Full Access

Effect of Richardson number on stagnation point flow of double diffusive mixed convective slip flow of magnetohydrodynamic Casson fluid: A numerical study

Corresponding Author

Mahantesh M. Nandeppanavar

[email protected]

Department of Studies and Research in Mathematics, Government College (Autonomous), Kalaburagi, Gulbarga, Karnataka, India

Correspondence

Mahantesh M. Nandeppanavar, Department of Studies and Research in Mathematics, Government College (Autonomous), Kalaburagi, Gulbarga, Karnataka, India.

Email: [email protected]

Search for more papers by this author

Kemparaju M. Chandrashekhar,

Kemparaju M. Chandrashekhar

Department of Mathematics, Centre for Incubation, Innovation Research and Consultancy, Jyothy Institute of Technology, Bengaluru, Karnataka, India

Search for more papers by this author

Raveendra Nagaraj,

Raveendra Nagaraj

Department of Mathematics, Rajarajeswari College of Engineering, Bengaluru, Karnataka, India

Search for more papers by this author

Mahantesh M. Nandeppanavar,

Corresponding Author

Mahantesh M. Nandeppanavar

[email protected]

Department of Studies and Research in Mathematics, Government College (Autonomous), Kalaburagi, Gulbarga, Karnataka, India

Correspondence

Mahantesh M. Nandeppanavar, Department of Studies and Research in Mathematics, Government College (Autonomous), Kalaburagi, Gulbarga, Karnataka, India.

Email: [email protected]

Search for more papers by this author

Kemparaju M. Chandrashekhar,

Kemparaju M. Chandrashekhar

Department of Mathematics, Centre for Incubation, Innovation Research and Consultancy, Jyothy Institute of Technology, Bengaluru, Karnataka, India

Search for more papers by this author

Raveendra Nagaraj,

Raveendra Nagaraj

Department of Mathematics, Rajarajeswari College of Engineering, Bengaluru, Karnataka, India

Search for more papers by this author

First published: 06 November 2021

https://doi.org/10.1002/cmm4.1209

Citations: 1

Share a link

Email
Wechat
Bluesky

Abstract

An analysis of stagnation point flow of heat and mass transfer of double diffusive mixed-convective stream with radiating vertical plate and convective boundary conditions. The Runge–Kutta method with shooting procedure is used to solve the transformed equations mathematically. An accuracy of the numerical procedure has been validated through a restriction of the current work compared with prior available results. The shear surface stress, Nusselt and Sherwood number are increased with increase in Prandtl number. The Biot number $Bi > 0.1$ is investigated and observed that to increase the Prandtl number, the friction coefficient, Nusselt number and Sherwood number are increased. The impact of pertinent constraints on distinct flow parameters are determined and analyzed through tables and graphs.

1 INTRODUCTION

Every one of the past scientists limited their examinations to stream and heat move for the Newtonian fluids. Various mechanical fluids, such as liquid plastics, polymeric fluids, blood and slurries, have recently been observed to exhibit non-Newtonian fluid behavior. Viscoelastic liquid, couple pressure liquid, micro polar liquid, power-law liquid, Casson liquid, and a variety of other non-Newtonian fluids are just a few examples. Non-Newtonian liquids have a lot of uses in design and industry, particularly in the extraction of unrefined petroleum from oil-based commodities. The Casson liquid is a non-Newtonian liquid with yield pressure, because of the chain structure of platelets and other variables, human blood may also be viewed as a Casson liquid. As a consequence, the Casson liquid has its own significance in both logical and designing territory such as extraction of plastic sheets, polythene and paper production, elastic sheets cooling, drawing of glass fiber, casting and rolling of hot plate, cosmetic process and wide uses in drug industries. The 2D magnetohydrodynamic (MHD) stagnation-point flow of non-Newtonian Casson fluid and heat transfer toward elongating sheet was proposed by Bhattacharyya.¹ Using warmth convective boundary constraints and fluid slip, combined heat and mass transfer through a moving radiating vertical flat plate was investigated by Beg et al.²In presence of velocity slip of MHD mixed convective flow with stagnation point over stretching sheet is analyzed by Shen et al.³

The current research explores the influence of nonlinear thermal radiation on the flow of a viscoelastic nanofluid in a double diffusive free convective boundary layer over a stretching wall. The existence of an applied magnetic field on electrically conducting fluid was analyzed by Kumar et al.⁴A study of a Casson fluid flow containing magnetic nanoparticles was conducted and the flow is believed to be over a paraboloid of the revolution's upper surface then considered results of viscous dissipation and nonlinear thermal radiation by Ramana Reddy et al.⁵ Mishra et al.⁶ studied the MHD stagnation point stream over a stretching sheet in presence of porous media. Mahantesh et al.⁷ considered the two-dimensional MHD stagnation point flow, heat and mass transfer in the presence of convective boundary conditions with the effect of thermal radiation. Thermal radiative MHD stagnation point slip stream and heat transmission induced by an elongating layer were investigated by Mahantesh et al.⁸ and Ramesh et al.,⁹ as well as enhancing radiation on hydro magnetic fields. A stretched cylinder of liquid-particle suspension receives Casson fluid flow. Kumar et al.¹⁰ explored the influence of nonlinear thermal radiation and a magnetic field on a double-diffusive convection flow. In the existence of a Darcian porous medium, Prasad et al.¹¹ investigated double diffusive impacts on mixed convection Casson fluid flow past a wavy inclined plate. Due to their numerous mechanical uses, such as the assembly of plastic sheets, the execution of greases and the formation of organic liquids, researchers are considering studying the properties of non-Newtonian liquids. The effect of radiative slip on MHD non-Newtonian stream of stretching sheet in presence of porous medium is analyzed by Kumar et al.¹² Mahantesh et al.¹³ demonstrated convective Casson fluid flow heat and mass transfer over a moving vertical plate using nonlinear thermal radiation and convective boundary constraints. Liaquat et al.¹⁴ and Liaquat et al.¹⁵ investigated the triple solution and stability analysis of Casson fluid stream of MHD stagnation point with thermal radiation and convective effects. Nagaraju et al.¹⁶ analyzed the slip and convective effects of MHD Casson fluid stream over a porous stretching sheet. Bouslimi et al.¹⁷ observed that the effects of soret and nonlinear mixed convective on MHD nanofluid stream of extending surface. Narendra et al.¹⁸ analyzed the radiation effects of Stagnation point flow of Casson fluid in presence of heat generation or absorption of nanofluid. The effects of nonlinear thermal radiation of heat and mass transfer of a double-diffusive moving vertical plate was investigated by Mahantesh et al.¹⁹ Vedavathi et al.²⁰ demonstrated the radiative effects of non-Darcy nanofluid with convective boundary conditions in presence of stretching surface. The effects of nonlinear thermal radiation on double diffusive stagnation point flow of convective moving plate was analyzed by Mahantesh et al.²¹

Inspired by the recently referenced examinations on progression of non-Newtonian liquids because of an extending sheet and its immense applications in numerous enterprises, in this article, the consistent two-dimensional MHD stagnation-point stream of electrically leading non-Newtonian Casson liquid and warmth move past an extending sheet in presence of warm radiation impact are researched. In this article, double diffusive MHD Casson fluid flow with Richardson number effect over a mixed convective slip flow investigates the mixed-convective flow of heat and mass transfer of double diffusive convective boundary conditions and velocity slip along a transmitting vertical level plate.

The examination has settled numerous application issues to discover the limit locale by utilizing shooting method. Because of what has been applied, the examination has arrived at that the shooting technique is the awesome most effortless approach to determine minor qualities issues, however there are a few detriments when utilizing the Newton Raphson's strategy for tallying starting worth, and afterward shooting's limit esteems, we track down that the mistake is bigger contrasting and Ode-RK4 strategy for checking the underlying qualities and afterward shooting limit esteems. At long last the examination has given a few suggestions and recommendations which one can resolve the limit esteems issues in extremely exact manner.

2 MATHEMATICAL MODEL

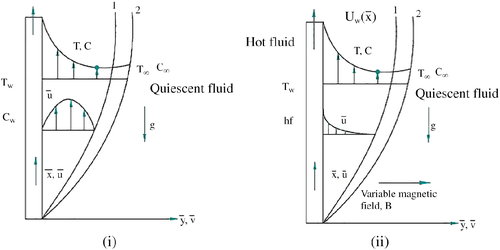
Considered geometry of the present study, in this $\overline{u}$ and $\overline{v}$ are velocity components along the rectangular coordinate system $\overline{x}$ and $\overline{y}$ as shown in Figure 1. The moving wall and fixed wall cases are shown in Figure 1A,B. The temperature of the unknown plate wall and the ambient fluid temperature are believed to be $T_{w} & T_{\infty}$ .

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Physical model of the problem

This result in a variable heat transport coefficient

h_{f} (x)

, uniform concentration of ambient fluid

C_{\infty}

, an unknown plate wall concentration

C_{w}

and applied transfer magnetic field

B (\overline{x})

along

\overline{y}

-axis are assumed. Except for density, fluid properties are considered to be invariant, changing only in response to changes in the flow. The external velocity (accelerating plate velocity)

u_{e} (x)

is of the forms

u_{e} (x) = {ax}^{\frac{1}{2}}

is assumed. The boundary layer equations that govern it are dimensional in nature.

\frac{\partial \overline{u}}{\partial \overline{x}} + \frac{\partial \overline{u}}{\partial \overline{y}} = 0,

()

ρ (\overline{u} \frac{\partial \overline{u}}{\partial \overline{x}} + \overline{v} \frac{\partial \overline{u}}{\partial \overline{y}}) = μ (1 + \frac{1}{β}) \frac{\partial^{2} \overline{u}}{\partial {\overline{y}}^{2}} + {\overline{u}}_{e} \frac{d {\overline{u}}_{e}}{d \overline{x}} + [ρ g β_{T} (T - T_{\infty}) + ρ g β_{C} (C - C_{\infty})] - σ_{0} B^{2} (\overline{x)} {\overline{u}}^{2},

()

\overline{u} \frac{\partial T}{\partial \overline{x}} + \overline{v} \frac{\partial T}{\partial \overline{y}} = (α + \frac{16 σ_{1} T^{3} \infty}{3 ρ c_{p} k_{1}}) \frac{\partial^{2} T}{\partial {\overline{y}}^{2}},

()

\overline{u} \frac{\partial C}{\partial \overline{x}} + \overline{v} \frac{\partial C}{\partial \overline{y}} = D \frac{\partial^{2} C}{\partial {\overline{y}}^{2}} .

()

The appropriate boundary conditions are

\begin{array}{l} \overline{v} = 0, \overline{u} = U_{w} + U_{slip} = U_{r} {(\frac{x}{L})}^{\frac{1}{2}} + N_{1} \frac{μ}{π} \frac{\partial \overline{u}}{\partial \overline{y}}, - k \frac{\partial T}{\partial \overline{y}} = h_{f} (\overline{x}) [T_{f} - T_{w}], C = C_{w} at \overline{y} = 0, \\ \overline{u} \to U_{e}, T \to T_{\infty}, C \to C_{\infty} as \overline{y} \to \infty \end{array}

()

where

k

the thermal conductivity,

\frac{μ}{ρ}

the kinematic viscosity,

β_{T}

the volumetric thermal coefficient,

N_{1}

the velocity slip factor,

B (\overline{x}) = \frac{B_{0}}{{\overline{x}}^{\frac{1}{2}}}

the variable magnetic field,

β_{C}

the volumetric concentration,

σ_{1}

is known as Stefan-Boltzmann constant,

k_{1}

mean absorption coefficient of Rosseland,

α = \frac{k}{ρ C_{p}}

the fluid's thermal diffusivity,

h_{f} (\overline{x})

the heat transfer coefficient,

σ = σ_{0} \overline{u}

the variable electric conductivity.

3 STANDARDIZATION OF THE GOVERNING EQUATIONS

The Equations (1-5) are expressed in dimensionless form by introducing the following

x = \frac{\overline{x}}{L}, y = \frac{\overline{y} {R_{e}}^{1 / 2}}{L}, u = \frac{\overline{u}}{U_{r}}, v = \frac{\overline{v} L}{υ {R_{e}}^{1 / 2}}, u_{e} = \frac{{\overline{u}}_{e}}{U_{r}}, θ = \frac{T - T_{\infty}}{T_{f} - T_{\infty}}, ϕ = \frac{C - C_{\infty}}{C_{w} - C_{\infty}} .

()

In order to acquire similarity answers for Equations (1-5), the stream function can be described as

u = \frac{\partial ψ}{\partial y}, v = - \frac{\partial ψ}{\partial x}

and to obtain the dimensionless equations are

\begin{array}{l} \frac{∂ψ}{\partial y} \frac{\partial^{2} ψ}{\partial x \partial y} - \frac{∂ψ}{\partial x} \frac{\partial^{2} ψ}{\partial y^{2}} - (1 + \frac{1}{β}) \frac{\partial^{3} ψ}{\partial y^{3}} - u_{e} \frac{{du}_{e}}{dx} - Ri [θ + Nϕ] + \frac{M}{x} {(\frac{∂ψ}{\partial y})}^{2} = 0, \end{array}

()

P_{r} (\frac{∂ψ}{\partial y} \frac{\partial θ}{\partial x} - \frac{∂ψ}{\partial x} \frac{\partial θ}{\partial y}) - (1 + R) \frac{\partial^{2} θ}{\partial y^{2}} = 0,

()

S_{c} (\frac{∂ψ}{\partial y} \frac{\partial φ}{\partial x} - \frac{∂ψ}{\partial x} \frac{\partial φ}{\partial y}) - \frac{\partial^{2} φ}{\partial y^{2}} = 0 .

()

The constraints on the boundary are

\frac{∂ψ}{\partial y} = x^{\frac{1}{2}} + \frac{{Re}^{\frac{1}{2}} N_{1} (x) μ}{L_{ρ}} \frac{\partial^{2} ψ}{\partial y^{2}}, \frac{∂ψ}{\partial x} = 0, \frac{\partial θ}{\partial y} = - \frac{{Lh}_{f} (x)}{k {Re}^{\frac{1}{2}}} (1 - θ), ϕ = 1, at y = 0,

\frac{∂ψ}{\partial y} \to U_{e}, θ \to 0, φ \to 0 as y \to \infty,

()

where

N = \frac{β_{C} (C_{w} - C_{\infty})}{β_{T} (T_{f} - T_{\infty})}

is called as buoyancy ratio parameter,

\Pr = \frac{υ}{α}

the Prandtl number,

M = \frac{σ_{0} B_{0}^{2}}{ρ}

the magnetic field parameter,

Sc = \frac{υ}{D}

the Schmidt number,

R = \frac{16 σ_{1} T_{\infty}^{3}}{3 k_{1} k}

the thermal radiation parameter,

Gr = \frac{ρ^{2} g β_{T} (T_{f} - T_{\infty}) L^{3}}{μ^{2}}

the Grashof number and

Ri = \frac{Gr}{{Re}^{2}}

the Richardson number. The Richardson number

Ri

is conveniently blended convective boundary. For

Ri < 0

have contradicting buoyance stream,

Ri > 0

have helping lightness stream and for

Ri = 0

the instance of absolutely constrained convective stream is recovered for which lightness impacts are absent.

4 UTILIZATION OF SIMILARITY EQUATIONS AND LINEAR GROUP ANALYSIS

The standardized Equations (7-9) and corresponding boundary constraints of Equation (10) are nonlinear coupled equations and these are highly complicated to solve. Likeness changes encourage arrangements. We expand on how a straight bunch of changes utilizing Lie group analysis. By using similarity variables to reduce the Equations (7-10) into ODE's. In order to do so, we use the terms independent and dependent variables as

x^{*} = {xC}^{β_{1}}, y^{*} = {yC}^{β_{2}}, ψ^{*} = ψ C^{β_{3}}, θ^{*} = θ C^{β_{4}}, φ^{*} = φ C^{β_{5}}, h_{f}^{*} = h_{f} C^{β_{6}}, N_{1}^{*} = N_{1} C^{β_{7}},

()

where

C

and

β_{i} (i = 1 \dots, 7)

are constants, we find the values of

β_{i}

by using the transformation. Equations

(7) – (10)

will be invariant if

β_{i}

are related by

β_{1} = 4 β_{2}, β_{3} = 3 β_{2}, β_{4} = β_{5} = 0, β_{6} = - β_{2}, β_{7} = β_{2} .

()

Total invariants are capacities that have a similar structure when changes occur, as seen through Equations (11) and (12) respectively.

\frac{y}{x^{\frac{1}{4}}} = \frac{y^{*}}{x^{* \frac{1}{4}}} .

()

As a consequence, under this set of transformations, this set of variables is invariant, meaning that it is a complete invariant. This useful structure is denoted by

η = \frac{y}{x^{\frac{1}{4}}} .

()

By these arguments, absolute invariants are

ψ = x^{\frac{3}{4}} F (η), θ = θ (η), φ = φ (η), h_{f} = x^{- \frac{1}{4}} {(h_{f})}_{0}, N_{1} = x^{\frac{1}{4}} {(N_{1})}_{0} .

()

Using similarity variables Equations (7-10) are converted to the following ODE

(1 + \frac{1}{β}) F^{'''} + \frac{3}{4} {FF}^{''} - \frac{1}{2} F^{'^{2}} - {MF}^{'^{2}} + λ + Ri θ + RiNϕ = 0,

()

(1 + R) θ^{''} + \frac{3}{4} \Pr {F θ}^{'} = 0,

()

ϕ^{''} + {Fϕ}^{'} + \frac{3}{4} Sc = 0 .

()

Subject to the limitations imposed by the boundaries

F (0) = 0, F^{'} (0) = 1 + {aF}^{''} (0), θ^{'} (0) = - Bi [1 - θ (0)], ϕ (0) = 1,

F^{'} (\infty) = λ, θ (\infty) = 0, ϕ (\infty) = 0,

()

where

a = {(N_{1})}_{0} υ {Re}^{\frac{1}{2}} / L

the slip factor and

Bi = {(h_{f})}_{0} L / {kRa}^{\frac{1}{2}}

the Biot number.

The neighborhood Nusselt number and the nearby Sherwood number are characterized as amounts of viable interest in this subject as

C_{f \overline{x}} = \frac{μ}{ρ U_{w}^{2} (\overline{x})} {(\frac{\partial \overline{u}}{\partial \overline{y}})}_{\overline{y} = 0}, {Nu}_{\overline{x}} = \frac{\overline{x}}{Δ T} {(- \frac{\partial T}{\partial \overline{y}})}_{\overline{y} = 0}, {Sh}_{\overline{x}} = \frac{\overline{x}}{Δ C} {(- \frac{\partial C}{\partial \overline{y}})}_{\overline{y} = 0} .

()

Using Equation (20) we obtain dimensionless versions of physical quantities are

{Re}_{\overline{x}}^{\frac{1}{2}} c_{f \overline{x}} = F^{''} (0), {Re}_{\overline{x}}^{- \frac{1}{2}} {Nu}_{\overline{x}} = - θ^{'} (0), {Re}_{\overline{x}}^{- \frac{1}{2}} {Sh}_{\overline{x}} = - ϕ^{'} (0) .

5 NUMERICAL METHOD OF SOLUTION

Equations (16)–(18) have been tackled mathematically with boundary conditions from Equation (19) along with shooting technique. By utilizing seventh order Runge–Kutta integration method, first we convert the original ODE's into first order ODE's by using

\begin{array}{l} p_{1} = F, p_{2} = F^{'}, p_{3} = F^{''}, p_{4} = θ, p_{5} = θ^{'}, p_{6} = ϕ, p_{7} = ϕ^{'} \\ p_{1}^{'} = p_{2}, \\ p_{2}^{'} = p_{3}, \\ p_{3}^{'} = (\frac{1}{(1 + \frac{1}{β})}) (- \frac{3}{4} p_{1} p_{3} + p_{2}^{2} (\frac{1}{2} + M) - λ - Ri (p_{4} + {Np}_{6})), \\ p_{4}^{'} = p_{5}, \\ p_{5}^{'} = - (\frac{3}{4 (1 + R)} \Pr p_{1} p_{5}), \\ p_{6}^{'} = p_{7}, \\ p_{7}^{'} = - \frac{3}{4} Sc p_{1} p_{7} \end{array}\} .

()

The initial conditions that apply are as follows:

\begin{array}{l} p_{1} (0) = 0, p_{2} (0) = 1 + a p_{3} (0), p_{5} (0) = - Bi (1 - p_{4} (0)), p_{6} (0) = 1 \\ p_{2} (\infty) = λ, p_{4} (\infty) = 0, p_{6} (\infty) = 0 \end{array}\} .

()

After choosing proper guess values for

u_{1} = F^{''} (0)

u_{2} = θ^{'} (0)

, and

u_{3} = ϕ^{'} (0)

, the integration is completed. By Newton's iterative method to compute the values of

u_{1}, u_{2}

, and

u_{3}

such that the solutions satisfy the boundary conditions at infinity with minimum error.

6 RESULTS AND DISCUSSION

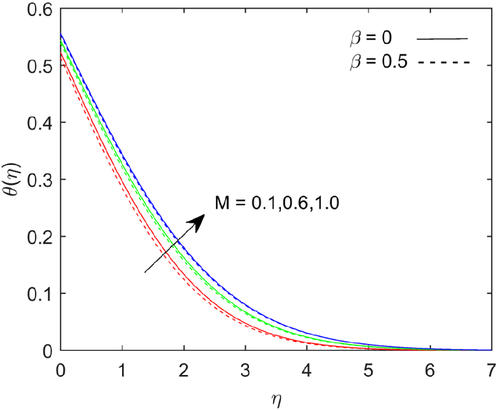
Equations (16-18) figured out with the boundary limitation Equation (19) are tackled for various assessments of the limit that depicts the stream appearances and the outcomes are explained through tables and graphs. The ${Re}_{x}^{1 / 2} C_{fx}$ (skin friction) decreases, ${Re}_{x}^{- 1 / 2} {Nu}_{x}$ (Nusselt number), and ${Re}_{x}^{- 1 / 2} {Sh}_{x}$ (Sherwood number) are slight increases, when increasing in the value of Prandtl number $\Pr$ . The flow is decelerated, due to thermal boundary layer thickness enhances with escalation in the Prandtl number, also it shows that there is a good agreement with existing results of Beg² and it showed in Table 1. Table 2 displays a good comparison with existing results of Beg.² When the value of magnetic field parameter $M$ , steadily decreases ${Re}_{x}^{1 / 2} C_{fx}$ (skin friction), the heat transfer rate ${Re}_{x}^{- 1 / 2} {Nu}_{x}$ (Nusselt number) and ${Re}_{x}^{- 1 / 2} {Sh}_{x}$ (Sherwood number) are decreases. The skin friction, heat transfer rate and mass transfer rate are maximized for electrically non conducting case $M = 0$ . The skin friction negative for $M > 0.8$ , because of influence strong magnetic field back flow is take place. We have discussed the flow, temperature and mass distribution through graphs. During the cooling of the plate, the numerical values of flow, heat, and mass distribution $(Gr > 0)$ , the value of thermal radiation parameter is equal to 1, the value of Richardson number is equal to 1 for both Newtonian $(β = 0)$ and non-Newtonian fluid $(β = 0.5)$ in all the graphs. Figure 1 shows flow configuration of the system.

TABLE 1. Friction coefficient, neighborhood Nusselt number and nearby Sherwood number for different estimations of Prandtl number when

M = 0.2, a = 1, Sc = 0.2, β = λ = 0, Ri = 1, Bi = 0.5, R = 1, and N = 1

$\Pr$	Present study	Beg²	Present study	Beg²	Present study	Beg²
	${Re}_{x}^{1 / 2} C_{fx}$		${Re}_{x}^{- 1 / 2} {Nu}_{x}$		${Re}_{x}^{- 1 / 2} {Sh}_{x}$
0.720	0.11881123	0.118720505	0.22137695	0.22133370545	0.2754326	0.27548183992
1.000	0.10086126	0.10074775	0.24353536	0.24349797543	0.2710455	0.27108671769
1.500	0.08047759	0.080943698	0.27033914	0.27030985823	0.2669517	0.26698704146
3.000	0.05097597	0.050822473	0.3135923	0.31357267765	0.262364	0.26239588936
6.000	0.02856726	0.028404019	0.35235239	0.35233841996	0.2597299	0.25976116717
10.000	0.01632061	0.016153229	0.37748658	0.37747541813	0.2585593	0.25859051021

TABLE 2. Friction coefficient, nearby Nusselt number and neighborhood Sherwood number for distinct estimations of

M

when

\Pr = 0.72, a = 1, Bi = 0.5, Sc = 0.2, β = λ = 0, Ri = 1, R = 1, and N = 1

$M$	Present study	Beg²	Present study	Beg²	Present study	Beg²
	${Re}_{x}^{1 / 2} C_{fx}$		${Re}_{x}^{- 1 / 2} {Nu}_{x}$		${Re}_{x}^{- 1 / 2} {Sh}_{x}$
0	0.18794831	0.187824583	0.22555281	0.22551012087	0.2842334	0.28426085002
0.2	0.11881123	0.118720505	0.22137695	0.22133370545	0.2754327	0.27548183992
0.4	0.06269274	0.052625256	0.21768361	0.21763995461	0.2678041	0.26787612507
0.5	0.03835591	0.038297286	0.21598766	0.21594382949	0.2643485	0.26443233378
0.6	0.01605037	0.015999146	0.21437941	0.21433541547	0.2610987	0.26119449011
0.8	−0.0234796	−0.023519489	0.21139501	0.21135067897	0.2551369	0.25525709211
1	−0.05753125	−0.057563295	0.20867753	0.20863285807	0.2497849	0.24993018990

Figure 2 shows enhance in the stagnation point parameter $λ$ , the flow rate is increases. The heat transfer rate and mass transfer rate are depicts slightly with an increase in stagnation point parameter $λ$ and it is shown in Figure 3 and Figure 4. The flow rate decelerates first and then steady when we escalates in Prandtl number, this it is been demonstrated in Figure 5.

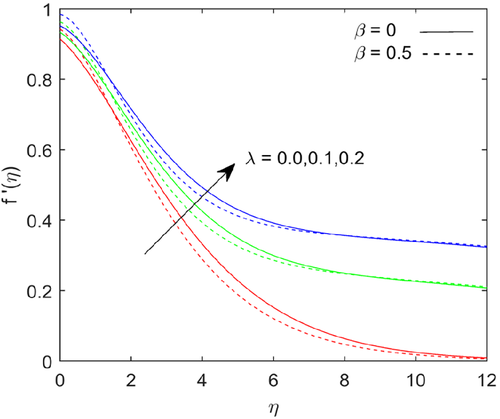
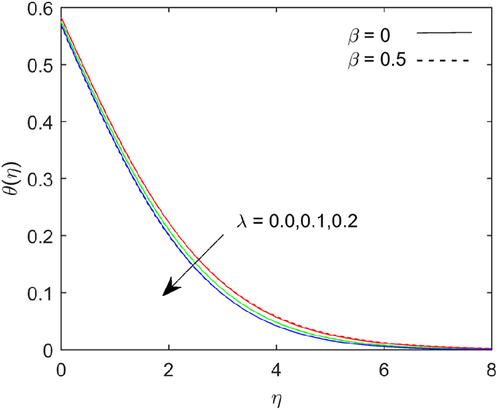
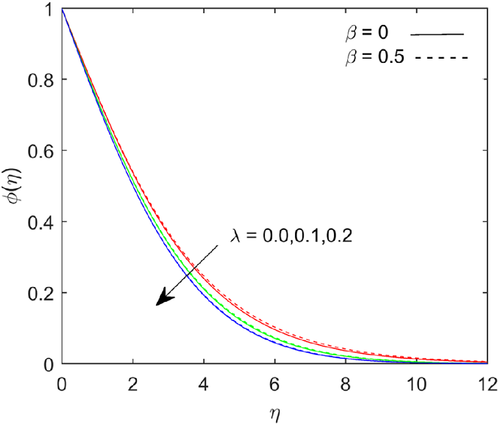
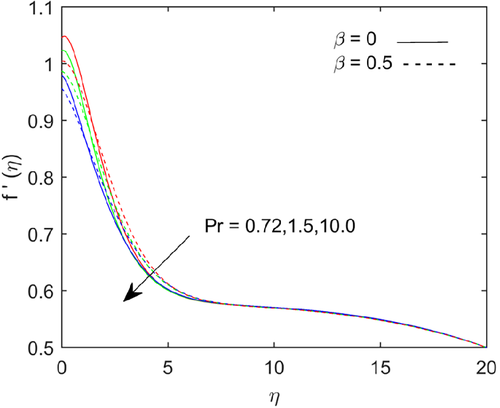
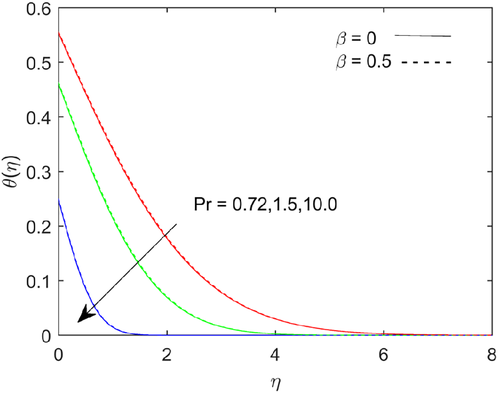
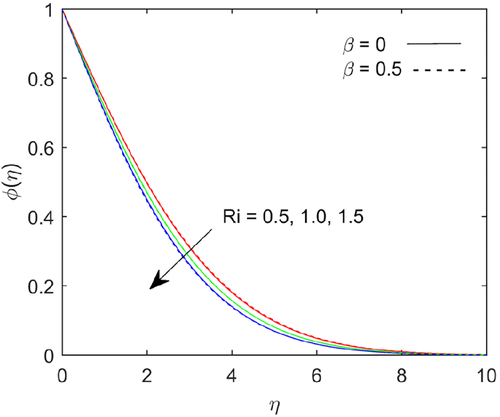
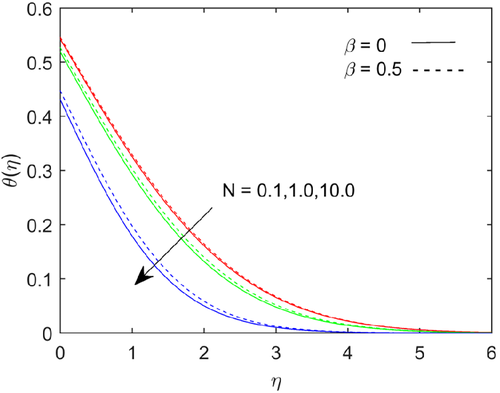
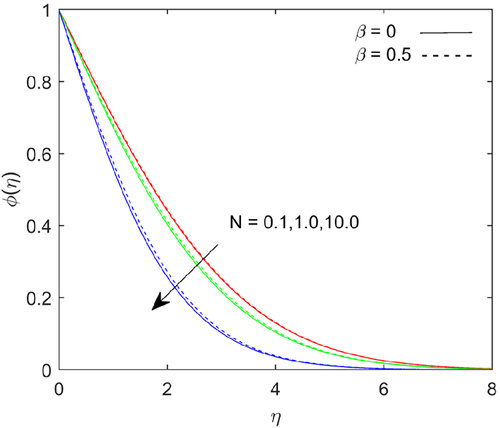
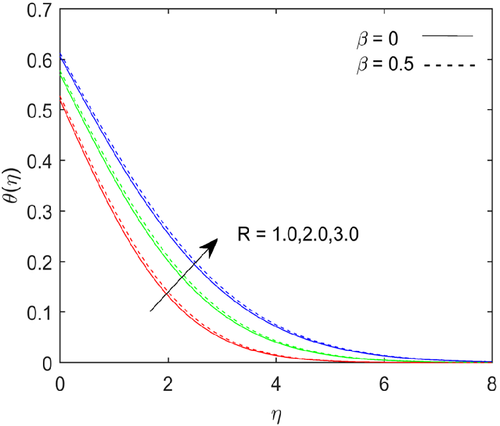
Figure 6 shows that temperature depicts with increases in Prandtl number $(\Pr)$ . Fluids exhibit higher viscosities with higher Prandtl number and it causes lower thermal conductivity. The Prandtl number signifies the ratio of momentum diffusivity to thermal diffusivity. The temperature magnitude falls with higher Prandtl number due to thermal diffusion rate decreases. Figures 7-9 shows the variations in flow, temperature and mass transfer rate for numerous values of Richardson number $(Ri)$ . The flow rate escalates; the heat and mass transfer rate reduces at the boundary with higher values of Richardson number. The energy and mass boundary layer thickness upraises with escalating the values of Richardson number.

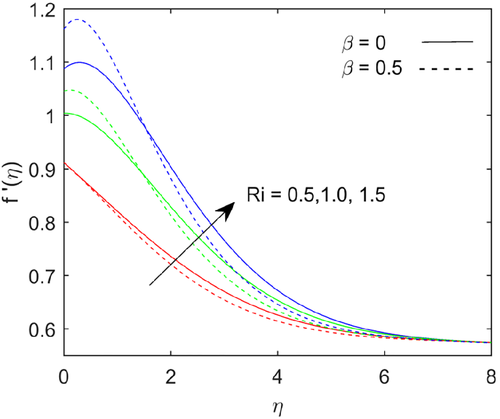
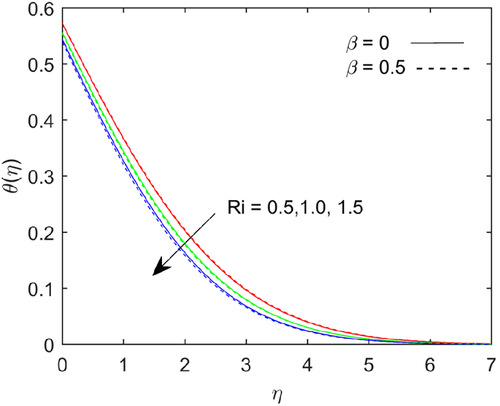
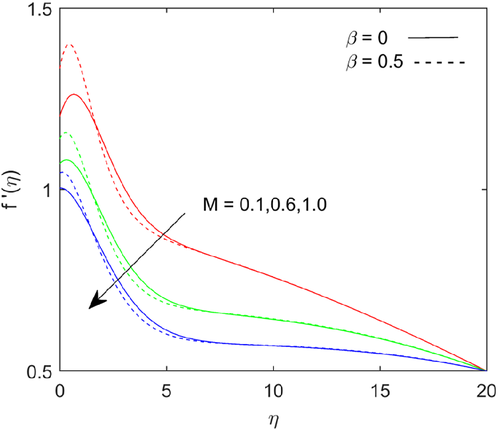
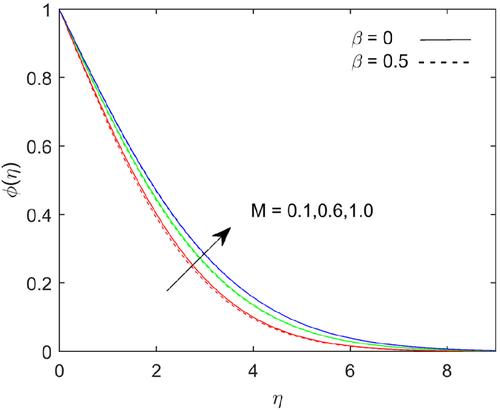
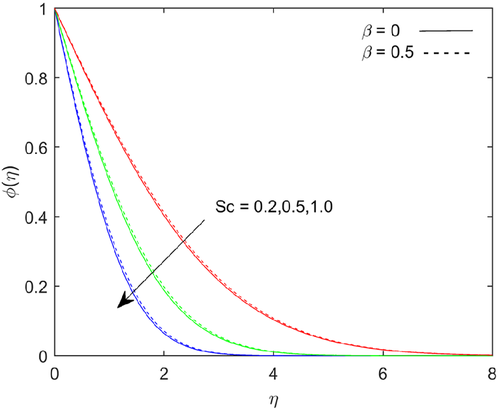
The escalation in magnetic field parameter $(M)$ , there is a strong resistance in the flow of fluid. The strong magnetic field retarding the body force due to an electrically conducting fluid. The Lorentz force drags the flow rate and it is shown in Figure 10. As the magnetic parameter increases, the thermal boundary layer thickness increases, due to that thermal energy enhances and it shown in Figure 11. The increasing in magnetic parameter the thermal diffusion field increases, which results in a small increase in concentration prolife, as seen in Figure 12. Figure 13 shows the effect of the buoyancy ratio parameter $(N)$ on temperature profile, the buoyancy ratio parameter suppress with rise in buoyancy ratio parameter. The concentration function depicts with rising in the value of buoyancy ratio parameter and it shows in the Figure 14. Figure 15 examines the pivotal performance of thermal radiation $(R)$ on temperature regime. The sketch indicates that as the value of thermal radiation increases, the thickness of the boundary layer increases, owing to the heat transfer rate scaling up at the boundary. The impact of Schmidt number $(Sc)$ on concentration distribution is plotted in Figure 16. It is observed that concentration distribution decelerates with scaling up Schmidt number. By definition Schmidt number represents the ratio of momentum diffusivity to the mass diffusivity. Increasing in Schmidt number means lower mass diffusivity, hence thinner in concentration boundary layers.

Note: While plotting the graphs the value of the governing parameter kept constant as: $N = 1, a = 1, M = 0.2, Ri = 1, \Pr = 0.72, R = 1, Bi = 0.1, Sc = 0.2, λ = 0.5, N = 1 .$

7 CONCLUSION

In this article explores stagnation point double diffusive MHD Casson fluid flow with Richardson number effect over a mixed convective slip flow. In previous literature the effects of Richardson number on stagnation point flow of Casson fluid with thermal radiation is not appeared by author's knowledge so for. So that the current work explored that an expansion of stagnation point flow and thermal radiation of Casson fluid is studied. The primary finishing up emphases are given below:

The flow rate enhances and energy transfer rate decreases with rising in the value of stagnation point parameter $λ$ .
The energy transfer rate and flow rate depicts with scaling up in Prandtl number.
The Richardson number has a greater effect on flow rate. The energy and mass transfer increases as the Richardson number grows.
By enriching the estimations of Casson parameter, the heat and mass transport rate slows and accelerates respectively.
The flow rate slowdowns and energy transfer rate increases with enhancing in magnetic parameter.

ACKNOWLEDGMENTS

Authors are thankful to the reviewers for their useful comments and suggestions, which helps to improve the quality of our paper.

CONFLICT OF INTEREST

The authors have no any type of conflict of interest.

Biographies

Dr. Mahantesh M. Nandeppanavar is presently working as Selection Grade Assistant Professor of Mathematics in Government College (Autonomous), Kalaburagi of Karnataka State, INDIA. He has published around 70 research articles in reputed international journals and 05 text books of Mathematics for undergraduate students. He has completed two major research projects and produced two Ph.Ds, Some more students are perusing Ph. D under his guidance.
Dr. Kemparaju M C is an Associate professor in the Department of Mathematics, Jyothy Institute of Technology, Bangalore (India). He obtained his Master's degree in Mathematics from Bangalore University in 2003 and received his Ph.D. degree from the Gulbarga University in 2018. His research interest is in Mathematical and Computational Modeling.
Dr Raveendra N born and brought up in the Chikkaballapur district of Karnataka, India. He obtained his Master's degree in Mathematics from the University of Alagappa in 2005 and received his Ph.D. degree from the Gulbarga University in 2018. He is now working in the Department of Mathematics, RajaRajeswari College of Engineering. His research interest covers the area of Boundary layer flows of Newtonian and non-Newtonian fluid, heat and mass transfer, flow through porous or non-porous media.

REFERENCES

1Bhattacharyya K. MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation. J Thermodyn. 2013; 169674: 1-9.
10.1155/2013/169674
Google Scholar
2Beg OA, Uddin MJ, Rashidi MM, Kavyani N. Double-diffusive radiative magnetic mixed convective slip flow with biot and Richardson number effects. J Eng Thermophys. 2014; 23(2): 79-97.
10.1134/S1810232814020015
CAS Web of Science® Google Scholar
3Shen M, Wang F, Chen H. MHD mixed convection slip flow near a stagnation- point on a nonlinearly vertical stretching sheet. Boundary Value Probl. 2015; 2015: 78.
10.1186/s13661-015-0340-6
Web of Science® Google Scholar
4 Ganesh Kumar K, Gireesha BJ, Manjunatha S, Rudraswamy NG. Effect of nonlinear thermal radiation on double-diffusive mixed convection boundary layer flow of viscoelastic nano fluid over a stretching sheet. Int J Mech Mater Eng. 2017; 12(18). doi:10.1186/s40712-017-0083-5
Google Scholar
5Ramana Reddy JV, Sugunamma V, Sandeep N. Enhanced heat transfer in the flow of dissipative non-Newtonian Casson fluid flow over a convectively heated upper surface of a paraboloid of revolution. J Mol Liq. 2017; 229: 380-388.
10.1016/j.molliq.2016.12.100
CAS Web of Science® Google Scholar
6Mishra SR, Nayak B, Sharma RP. MHD stagnation-point flow past over a stretching sheet in the presence of non-Darcy porous medium and heat source/sink. Defect Diffus Forum. 2017; 374: 92-105.
10.4028/www.scientific.net/DDF.374.92
Google Scholar
7Nandeppanavar MM, Subhas Abel M, Kemparaju MC. Effect of thermal radiation and velocity slip on stagnation point flow, heat and mass transfer of hydro magnetic nanofluid due to stretching surface with convective boundary condition. J Nano Fluids. 2017; 6: 1-10.
Google Scholar
8Nandeppanavar MM, Kemparaju MC, Subhas Abel M. Thermal radiative MHD stagnation point slip flow and heat transfer due to a stretching sheet. J Nano Fluids. 2018; 7: 1-8.
Google Scholar
9Ramesh GK, Ganesh Kumar K, Shehzad SA, Gireesha BJ. Enhancement of radiation on hydro magnetic Casson fluid flow towards a stretched cylinder with suspension of liquid-particles. Can J Phys. 2018; 96(1): 18-24.
10.1139/cjp-2017-0307
CAS Web of Science® Google Scholar
10Ganesh Kumar K, Ramesh GK, Gireesha BJ, Rashad AM. Double-diffusive convection flow of Casson fluid with nonlinear thermal radiation and convective condition. Commun Numer Anal. 2018; 1: 81-99.
10.5899/2018/cna-00350
Google Scholar
11Krishna Prasad DV, Krishna Chaitanya GS, Srinivasa Raju R. Double diffusive effects on mixed convection Casson fluid flow past a wavy inclined plate in presence of Darcian porous medium. Results Eng. 2019; 3: 3-100019.
Google Scholar
12Anantha Kumar K, Sugunamma V, Sandeep N, Ramana Reddy JV. Numerical examination of MHD nonlinear radiative slip motion of non-Newtonian fluid across a stretching sheet in the presence of a porous medium. Heat Transf Res. 2019; 50(12): 1163-1181.
10.1615/HeatTransRes.2018026700
Web of Science® Google Scholar
13Nandeppanavar MM, Kemparaju MC, Raveendra N. Double-diffusive free convective flow of Casson fluid due to a moving vertical plate with non-linear thermal radiation. World J Eng. 2020; 18(1): 85-93.
10.1108/WJE-06-2020-0215
Web of Science® Google Scholar
14Lund LA, Omar Z, Khan I, Baleanu D, Nisar KS. Convective effect on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a vertical exponentially stretching/shrinking surface: triple solutions. Symmetry. 2020; 12: 1238.
10.3390/sym12081238
CAS Web of Science® Google Scholar
15Lund LA, Omar Z, Khan I, Baleanu D, Nisar KS. Dual similarity solutions of MHD stagnation point flow of Casson fluid with effect of thermal radiation and viscous dissipation: stability analysis. Sci Rep. 2020; 10:15405.
10.1038/s41598-020-72266-2
CAS PubMed Web of Science® Google Scholar
16Raju TN, Krishna YH, Krishna GV, Vijaya N. Slip effect of mixed convective MHD casson fluid flow over vertical permeable stretching sheet in a porous medium. J Crit Rev. 2020; 17(7): 1316-1325.
Google Scholar
17Bouslimi J, Abdelhafez MA, Abd-Alla AM, Abo-Dahab SM, Mahmoud KH. MHD mixed convection nanofluid flow over convectively heated nonlinear due to an extending surface with soret effect. Complexity. 2021; 2021(20):5592024.
10.1155/2021/5592024
Google Scholar
18Narendra G, Govardhan K, Sarma GS. Magnetohydrodynamic stagnation point on a Casson nanofluid flow over a radially stretching sheet. Beilstein J Nanotechnol. 2020; 11: 1303-1315.
10.3762/bjnano.11.114
PubMed Web of Science® Google Scholar
19Nandeppanavar MM, Kemparaju MC, Raveendra N. Double-diffusive natural convective stream due to moving vertical plate with nonlinear thermal radiation and Newton's boundary constraint. Heat Transf. 2021; 50: 4694-4707.
10.1002/htj.22096
Web of Science® Google Scholar
20Vedavathi N, Dharmaiah G, Venkatadri K, Gaffar SA. Numerical study of radiative non-Darcy nanofluid flow over a stretching sheet with a convective Nield conditions and energy activation. Nonlinear Eng. 2021; 10: 159-176.
10.1515/nleng-2021-0012
Google Scholar
21 Nandeppanavar MM, Kemparaju MC, Raveendra N. Effect of non-linear thermal radiation on the stagnation point flow of double diffusive free convection due to moving vertical plate. J Eng Des Technol. 2021. doi:10.1108/JEDT-10-2020-0430
Web of Science® Google Scholar

Citing Literature

All articles

Effect of Richardson number on stagnation point flow of double diffusive mixed convective slip flow of magnetohydrodynamic Casson fluid: A numerical study

Abstract

1 INTRODUCTION

2 MATHEMATICAL MODEL

3 STANDARDIZATION OF THE GOVERNING EQUATIONS

4 UTILIZATION OF SIMILARITY EQUATIONS AND LINEAR GROUP ANALYSIS

5 NUMERICAL METHOD OF SOLUTION

6 RESULTS AND DISCUSSION

7 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Effect of Richardson number on stagnation point flow of double diffusive mixed convective slip flow of magnetohydrodynamic Casson fluid: A numerical study

Abstract

1 INTRODUCTION

2 MATHEMATICAL MODEL

3 STANDARDIZATION OF THE GOVERNING EQUATIONS

4 UTILIZATION OF SIMILARITY EQUATIONS AND LINEAR GROUP ANALYSIS

5 NUMERICAL METHOD OF SOLUTION

6 RESULTS AND DISCUSSION

7 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information