Volume 3, Issue 6 e1204

SPECIAL ISSUE PAPER

Full Access

Pricing passport option using higher order compact scheme

Ankur Kanaujiya,

Ankur Kanaujiya

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, India

Search for more papers by this author

Siddhartha P. Chakrabarty,

Corresponding Author

Siddhartha P. Chakrabarty

[email protected]

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, India

Correspondence Siddhartha P. Chakrabarty, Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam 781039, India.

Email: [email protected]

Search for more papers by this author

Ankur Kanaujiya,

Ankur Kanaujiya

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, India

Search for more papers by this author

Siddhartha P. Chakrabarty,

Corresponding Author

Siddhartha P. Chakrabarty

[email protected]

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, India

Correspondence Siddhartha P. Chakrabarty, Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam 781039, India.

Email: [email protected]

Search for more papers by this author

First published: 10 October 2021

https://doi.org/10.1002/cmm4.1204

Funding information: There are no funders to report for this submission.

Share a link

Email
Wechat
Bluesky

Abstract

Higher order compact scheme (HOC) is used for pricing both European and American type passport option. We consider the problem for two different cases, namely, the symmetric case (which has a closed form solution) and the non-symmetric case. For the symmetric case HOC schemes result in slightly improved results as compared to the classical Crank–Nicolson implicit method, while still giving approximately second order convergence rate. In order to improve the convergence rate, grid stretching near zero accumulated wealth is introduced in the HOC schemes. The consequent higher order compact scheme with grid stretching gives better results with the rate of convergence being close to third order. For non-symmetric case we also observe similar results for both European and American type passport option. In absence of any analytic formula for the non-symmetric case, convergence rate was calculated using double-mesh differences.

1 INTRODUCTION

Passport options having a trading account as the underlying was designed at the Bankers Trust in 1997¹ with the purpose of hedging against losses incurred by the trading account. The passport option is effectively a call option on the balance of a trading account,² wherein the holder retains the gains from the trading account during the life of the option. In particular, Hyer et al.¹ consider trading on an asset, with the price and number of units held at time t, being denoted by

S (t)

and

u (t)

, respectively, with

u (t) \in [- 1, 1]

. Consequently, at expiration T, the holder will receive an amount of

\max (w (T), 0)

from the writer, with

w (t)

denoting accumulated wealth at time t. Accordingly, in a complete market, the price of the passport option is given by

𝒱 (S, w, t) = \sup_{| u (t) | < 1} 𝔼_{*} \{e^{- r (T - t)} \max (w (T), 0) | S (t) = S, w (t) = w\},

where r is the riskfree rate and

𝔼_{*}

is the expectation under the risk-neutral measure

ℙ^{*}

. Using the pricing partial differential equation (PDE) approach, the valuation PDE for passport option (after using the transformation

x = w / S

) is given by References 2, 3,

\frac{\partial v}{\partial t} + (u^{*} - x) (r - γ) \frac{\partial v}{\partial x} + \frac{1}{2} {(u^{*} - x)}^{2} σ^{2} \frac{\partial^{2} v}{\partial x^{2}} = γ v, x \in ℝ, t \in [0, T] .

()

where

v (x, t)

is the transformed option price and

u^{*} = sign ((r - γ) \frac{\partial v}{\partial x} - x σ^{2} \frac{\partial^{2} v}{\partial x^{2}}) .

()

Here

σ

is the volatility of the geometric Brownian motion (GBM) driven asset pricing model for

S (t)

and

γ

is the cost of carry, with

u^{*}

representing the optimal trading strategy chosen by the holder of the option. Taking into account the non-existence of a closed form pricing formula in the nonsymmetric case, where the riskfree rate is not identical to the cost of carry (a closed form solution exists for the symmetric case when both are identical), several numerical approaches to this pricing problem have been adopted. The numerical approaches were designed essentially for obtaining the numerical solution to the PDE. Various theoretical and numerical aspects of passport options, as well as options on trading account can be found in References 2-18. Obtaining precise and accurate solutions to PDEs on a compact stencil can be accomplished through higher order compact (HOC) schemes. Several HOC schemes for problems with both Dirichlet and Neumann boundary conditions have appeared in References 19-23 and have found applications in pricing of options as well.^{24, 25} Given the specific nature of the pricing PDE for passport options, we are interested in those HOC schemes which do not require the coefficients to be smooth.^{22, 23, 26, 27} In this article, we construct a set of fourth-order HOC schemes for the pricing of European passport option (on a trading account whose value is contingent on the price of a traded risky security), for which the boundary conditions are both Dirichlet and Neumann in nature. The set of schemes presented are fourth order accurate in space at all the grid points including both the interior and boundary points. The boundary conditions at the boundaries,

x_{\min} = - \exp (4 σ \sqrt{T})

and

x_{\max} = \exp (4 σ \sqrt{T})

along with the final condition are as follows:

\begin{align} v (x_{\min}, t) & = 0, \end{align}

()

\begin{align} v_{x} (x_{\max}, t) & = e^{- r (T - t)}, \end{align}

()

\begin{align} v (x, T) & = \max (x, 0) . \end{align}

()

Equation (1) can be written as

\frac{\partial v}{\partial t} + 𝒜 (x, u^{*}) \frac{\partial v}{\partial x} + ℬ (x, u^{*}) \frac{\partial^{2} v}{\partial x^{2}} = γ v,

()

where

𝒜 (x, u^{*}) = (u^{*} - x) (r - γ)

and

ℬ (x, u^{*}) = \frac{1}{2} {(u^{*} - x)}^{2} σ^{2}

2 THE HIGHER ORDER COMPACT SCHEMES

We present the compact difference schemes both for the interior as well as the boundary points, following the approach in Reference 22. Accordingly, let

Δ t

denote the uniform temporal mesh size with the m-th time point being

t^{m} = m Δ t, 0 \leq m \leq N

, where N is the number of temporal intervals and

Δ t = \frac{T}{N}

. For the spatial uniform mesh, we consider M spatial points

x_{j} = x_{\min} + (j - 1) Δ x

1 \leq j \leq M

, with the mesh size being

Δ x = \frac{x_{\max} - x_{\min}}{(M - 1)}

. The approximation of

v (x, t)

v_{x} (x, t)

v_{x x} (x, t)

, and

u^{*} (x, t)

at the point

(x_{j}, t^{m})

are denoted by

v_{j}^{m}

{(v_{x})}_{j}^{m}

{(v_{x x})}_{j}^{m}

, and

{(u^{*})}_{j}^{m}

, respectively. We note that the time discretization of Equation (6) using the Crank–Nicolson implicit method (CNIM) is given by,

\frac{v_{j}^{m + 1} - v_{j}^{m}}{Δ t} + 𝒜 (x_{j}, {(u^{*})}_{j}^{m + 1}) [\frac{{(v_{x})}_{j}^{m + 1} + {(v_{x})}_{j}^{m}}{2}] + ℬ (x_{j}, {(u^{*})}_{j}^{m + 1}) [\frac{{(v_{x x})}_{j}^{m + 1} + {(v_{x x})}_{j}^{m}}{2}] = γ [\frac{v_{j}^{m + 1} + v_{j}^{m}}{2}] .

()

We now construct the fourth-order approximation for the term ${(v_{x})}_{j}^{m}$ and ${(v_{x x})}_{j}^{m}$ .

2.1 The interior points

We first consider all the interior points

(x_{j}, t^{m})

, where

3 \leq j \leq M - 2

and

0 \leq m \leq N - 1

. The following compact schemes^{26, 27} are used to derive a fourth-order approximation to

{(v_{x})}_{j}^{m}

and

{(v_{x x})}_{j}^{m}

\begin{align} a_{1} {(v_{x})}_{j + 1}^{m} + b_{1} {(v_{x})}_{j}^{m} + c_{1} {(v_{x})}_{j - 1}^{m} = \frac{v_{j + 1}^{m} - v_{j - 1}^{m}}{2 Δ x}, \end{align}

()

\begin{align} a_{2} {(v_{x x})}_{j + 1}^{m} + b_{2} {(v_{x x})}_{j}^{m} + c_{2} {(v_{x x})}_{j - 1}^{m} = \frac{v_{j + 1}^{m} - 2 v_{j}^{m} + v_{j - 1}^{m}}{{(Δ x)}^{2}} . \end{align}

()

where the coefficients are determined by matching the Taylor series expansion up to fourth order terms in

Δ x

and are,

a_{1} = c_{1} = \frac{1}{6}, b_{1} = \frac{2}{3} and a_{2} = c_{2} = \frac{1}{12}, b_{2} = \frac{5}{6} .

Substituting these values in (8) and (9) we obtain,

\begin{align} \frac{1}{4} {(v_{x})}_{j + 1}^{m} + {(v_{x})}_{j}^{m} + \frac{1}{4} {(v_{x})}_{j - 1}^{m} & = \frac{3}{2} [\frac{v_{j + 1}^{m} - v_{j - 1}^{m}}{2 Δ x}], 3 \leq j \leq M - 2, 0 \leq m \leq N - 1 . \end{align}

()

\begin{align} \frac{1}{10} {(v_{x x})}_{j + 1}^{m} + {(v_{x x})}_{j}^{m} + \frac{1}{10} {(v_{x x})}_{j - 1}^{m} & = \frac{6}{5} [\frac{v_{j + 1}^{m} - 2 v_{j}^{m} + v_{j - 1}^{m}}{{(Δ x)}^{2}}], 3 \leq j \leq M - 2, 0 \leq m \leq N - 1 . \end{align}

()

2.2 The boundary points

We next consider the fourth order approximation to

{(v_{x})}_{2}^{m}

{(v_{x x})}_{2}^{m}

{(v_{x})}_{M - 1}^{m}

, and

{(v_{x x})}_{M - 1}^{m}

near the actual boundary points

x_{1}

and

x_{M}

. At the left boundary

(x_{1}, t^{m})

we have the Dirichlet boundary condition,

v (x_{1}, t^{m}) = 0

. The following compact schemes are used to derive a fourth-order approximation to

{(v_{x})}_{2}^{m}

and

{(v_{x x})}_{2}^{m}

for

0 \leq m \leq N - 1

\begin{align} d_{1} {(v_{x})}_{2}^{m} + e_{1} {(v_{x})}_{3}^{m} & = \frac{1}{Δ x} (f_{1} v_{1}^{m} + g_{1} v_{2}^{m} + h_{1} v_{3}^{m}), \end{align}

()

\begin{align} {(v_{x x})}_{2}^{m} + k {(v_{x x})}_{3}^{m} & = \frac{1}{{(Δ x)}^{2}} (k_{1} v_{1}^{m} + k_{2} v_{2}^{m} + k_{3} v_{3}^{m} + k_{4} v_{4}^{m} + k_{5} v_{5}^{m} + k_{6} v_{6}^{m}), \end{align}

()

where the coefficients are determined by matching the Taylor series expansion up to fourth order terms in

Δ x

and are,

d_{1} = 4, e_{1} = 2, f_{1} = - 1, g_{1} = - 4, h_{1} = 5 and k = \frac{1}{2}, k_{1} = \frac{19}{24}, k_{2} = - \frac{7}{12}, k_{3} = - \frac{19}{12}, k_{4} = \frac{11}{6}, k_{5} = - \frac{13}{24}, k_{6} = \frac{1}{12} .

Substituting these values in (12) and (13) we obtain,

4 {(v_{x})}_{2}^{m} + 2 {(v_{x})}_{3}^{m} = \frac{1}{Δ x} (- v_{1}^{m} - 4 v_{2}^{m} + 5 v_{3}^{m}) .

()

{(v_{x x})}_{2}^{m} + \frac{1}{2} {(v_{x x})}_{3}^{m} = \frac{1}{{(Δ x)}^{2}} (\frac{19}{24} v_{1}^{m} - \frac{7}{12} v_{2}^{m} - \frac{19}{12} v_{3}^{m} + \frac{11}{6} v_{4}^{m} - \frac{13}{24} v_{5}^{m} + \frac{1}{12} v_{6}^{m}) .

()

At the right boundary

(x_{M}, t^{m})

we have the Neumann boundary condition,

v_{x} (x_{M}, t^{m}) = e^{- r (T - t^{m})}

. The following compact schemes are used to derive a fourth-order approximation to

{(v_{x})}_{M - 1}^{m}

and

{(v_{x x})}_{M - 1}^{m}

\begin{align} d_{2} {(v_{x})}_{M - 2}^{m} + e_{2} {(v_{x})}_{M - 1}^{m} + f_{2} {(v_{x})}_{M}^{m} & = \frac{1}{(Δ x)} (g_{2} v_{M - 1}^{m} + h_{2} v_{M - 2}^{m}), \end{align}

()

\begin{align} d_{3} {(v_{x x})}_{M - 2}^{m} + e_{3} {(v_{x x})}_{M - 1}^{m} + \frac{1}{Δ x} f_{3} {(v_{x})}_{M}^{m} & = \frac{1}{{(Δ x)}^{2}} (g_{3} v_{M - 1}^{m} + h_{3} v_{M - 2}^{m}), \end{align}

()

where the coefficients are determined by matching the Taylor series expansion up to fourth order terms in

Δ x

and are,

d_{2} = 5, e_{2} = 8, f_{2} = - 1, g_{2} = 12, h_{2} = - 12 and d_{3} = - 1 / 3, e_{3} = 11 / 6, f_{3} = - 1, g_{3} = - 1, h_{3} = 1 .

Substituting these values in (16) and (17) we obtain,

\begin{align} 5 {(v_{x})}_{M - 2}^{m} + 8 {(v_{x})}_{M - 1}^{m} & = {(v_{x})}_{M}^{m} + \frac{1}{Δ x} (12 v_{M - 1}^{m} - 12 v_{M - 2}^{m}) . \end{align}

()

\begin{align} (- 4) {(v_{x x})}_{M - 2}^{m} + 22 {(v_{x x})}_{M - 1}^{m} & = \frac{12}{Δ x} {(v_{x})}_{M}^{m} + \frac{1}{{(Δ x)}^{2}} (- 12 v_{M - 1}^{m} + 12 v_{M - 2}^{m}) . \end{align}

()

Thus the set of schemes, consisting of (7), (10), (11), (14), (15), (18), and (19) has the overall order of $O ({(Δ t)}^{2} + {(Δ x)}^{4})$ .

We now introduce a few notations prior to representing the numerical scheme (7) in the matrix form. At the time level

t^{m}, 0 \leq m \leq N - 1

, we have

({\vec{v}}^{m}) = {(v_{2}^{m}, \dots, v_{M - 1}^{m})}^{⊤}, {({\vec{v}}_{x})}^{m} = {({(v_{x})}_{2}^{m}, \dots, {(v_{x})}_{M - 1}^{m})}^{⊤}, {({\vec{v}}_{x x})}^{m} = {({(v_{x x})}_{2}^{m}, \dots, {(v_{x x})}_{M - 1}^{m})}^{⊤}

\begin{align} A & = [\begin{matrix} 1 & \frac{1}{2} \\ 1 & 10 & 1 \\ ⋱ & ⋱ & ⋱ \\ 1 & 10 & 1 \\ - 4 & 22 \end{matrix}], B = [\begin{matrix} - 7 / 24 & - 19 / 24 & 11 / 12 & - 13 / 48 & 1 / 24 & \dots \\ 6 & - 12 & 6 \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ 6 & - 12 & 6 \\ 6 & - 6 \end{matrix}], \end{align}

()

\begin{align} D & = [\begin{matrix} 4 & 2 \\ 1 & 4 & 1 \\ ⋱ & ⋱ & ⋱ \\ 1 & 4 & 1 \\ 5 & 8 \end{matrix}], E = [\begin{matrix} - 4 & 5 \\ - 3 & 0 & 3 \\ ⋱ & ⋱ & ⋱ \\ - 3 & 0 & 3 \\ - 12 & 12 \end{matrix}] . \end{align}

()

\begin{align} {(\vec{C})}^{m} & = {(\frac{19}{24 {(Δ x)}^{2}} v_{1}^{m}, 0, \dots, 0, \frac{12}{Δ x} {(v_{x})}_{M}^{m})}^{⊤}, {(\vec{F})}^{m} = {(- \frac{1}{Δ x} v_{1}^{m}, 0, \dots, 0, {(v_{x})}_{M}^{m})}^{⊤} . \end{align}

()

Using these notations, the schemes in (11), (15), and (19) can be written as

A {({\vec{v}}_{x x})}^{m} = \frac{2}{{(Δ x)}^{2}} B {(\vec{v})}^{m} + {(\vec{C})}^{m}

()

Similarly, the schemes in (10), (14), and (18) can be written as

D {({\vec{v}}_{x})}^{m} = \frac{1}{Δ x} E {(\vec{v})}^{m} + {(\vec{F})}^{m} .

()

The invertibility of matrices A and D shows the solvability of (23) and (24) which can be proved using the Gerschgorin theorem.²⁸ Simplifying (23) and (24) we obtain

\begin{align} {({\vec{v}}_{x x})}^{m} & = \frac{2}{{(Δ x)}^{2}} A^{- 1} B {(\vec{v})}^{m} + A^{- 1} {(\vec{C})}^{m} . \end{align}

()

\begin{align} {({\vec{v}}_{x})}^{m} & = \frac{1}{Δ x} D^{- 1} E {(\vec{v})}^{m} + D^{- 1} {(\vec{F})}^{m} . \end{align}

()

Using (25) and (26) in the CNIM (7) we obtain,

\begin{align} \frac{{(\vec{v})}^{m + 1} - {(\vec{v})}^{m}}{Δ t} + \frac{1}{2 Δ x} S^{m + 1} D^{- 1} E [{(\vec{v})}^{m + 1} + {(\vec{v})}^{m}] + \frac{1}{2} S^{m + 1} D^{- 1} [{(\vec{F})}^{m + 1} + {(\vec{F})}^{m}] \\ + \frac{1}{{(Δ x)}^{2}} R^{m + 1} A^{- 1} B [{(\vec{v})}^{m + 1} + {(\vec{v})}^{m}] + \frac{1}{2} R^{m + 1} A^{- 1} [{(\vec{C})}^{m + 1} + {(\vec{C})}^{m})] = \frac{γ}{2} [{(\vec{v})}^{m + 1} + {(\vec{v})}^{m})], \end{align}

()

where R and S are diagonal matrices given by

\begin{align} S^{m + 1} & = diag (α_{2}^{m + 1}, α_{3}^{m + 1}, \dots α_{M - 1}^{m + 1}), α_{j}^{m + 1} = 𝒜 (x_{j}, {(u^{*})}_{j}^{m + 1}), \\ R^{m + 1} & = diag (β_{2}^{m + 1}, β_{3}^{m + 1}, \dots β_{M - 1}^{m + 1}), β_{j}^{m + 1} = ℬ (x_{j}, {(u^{*})}_{j}^{m + 1}) . \end{align}

()

Upon further simplification, (27) becomes

\begin{align} [(1 + \frac{γ Δ t}{2}) I - \frac{1}{2} q S^{m + 1} D^{- 1} E - p R^{m + 1} A^{- 1} B] {(\vec{v})}^{m} \\ = [(1 - \frac{γ Δ t}{2}) I + \frac{1}{2} q S^{m + 1} D^{- 1} E + p R^{m + 1} A^{- 1} B] {(\vec{v})}^{m + 1} \\ + \frac{Δ t}{2} S^{m + 1} D^{- 1} [{(\vec{F})}^{m + 1} + {(\vec{F})}^{m}] + \frac{Δ t}{2} R^{m + 1} A^{- 1} [{(\vec{C})}^{m + 1} + {(\vec{C})}^{m})], \end{align}

()

where I is the identity matrix of size

(M - 2) \times (M - 2)

p = \frac{Δ t}{{(Δ x)}^{2}}

and

q = \frac{Δ t}{Δ x}

The discretization of

u^{*}

in (2) using the HOC schemes is

{(u^{*})}_{j}^{m} = sign (\frac{(r - γ)}{2} [{(v_{x})}_{j}^{m + 1} + {(v_{x})}_{j}^{m}] - \frac{1}{2} x_{j} σ^{2} [{(v_{x x})}_{j}^{m + 1} + {(v_{x x})}_{j}^{m}]),

()

which upon further simplification using (25) and (26) results in

\begin{align} {\vec{(u^{*})}}^{m} & = sign (\frac{(r - γ)}{2 Δ x} D^{- 1} E [{(\vec{v})}^{m + 1} + {(\vec{v})}^{m}] + \frac{(r - γ)}{2} D^{- 1} [{(\vec{F})}^{m + 1} + {(\vec{F})}^{m}] \\ - σ^{2} \frac{1}{{(Δ x)}^{2}} T A^{- 1} B [{(\vec{v})}^{m + 1} + {(\vec{v})}^{m}] - \frac{σ^{2}}{2} T A^{- 1} [{(\vec{C})}^{m + 1} + {(\vec{C})}^{m}]) . \end{align}

()

where

{\vec{(u^{*})}}^{m} = {({(u^{*})}_{2}^{m}, \dots, {(u^{*})}_{M - 1}^{m})}^{⊤}

and T is the diagonal matrix given by

T = diag (x_{2}, x_{3}, \dots, x_{M - 1}) .

()

We developed a HOC scheme in space and used Crank–Nicolson scheme for the time discretization only. For the purpose of subsequent discussion, HOC scheme would mean HOC scheme in space and Crank–Nicolson scheme in time, as detailed in this section.

3 GRID STRETCHING

While HOC schemes result in better convergence as compared to the CNIM, we observed that such improvement using HOC schemes is somewhat limited near the zero accumulated gain. The payoff (final condition) for the passport option is non-smooth at the zero accumulated wealth. Since the accuracy of a finite difference approximation depends on the existence of several derivatives in the Taylor's series approximation, but at zero accumulated wealth, the payoff is not differentiable, therefore in order to improve the accuracy, we need the local mesh refinement near the zero accumulated wealth. Therefore, in order to improve the convergence rate as well as reduce the maximum error due to non-smooth nature of the final condition, we use a stretching transformation^{24, 25} to obtain HOC schemes with grid stretching (HOCGS). The transform using the transformed coordinate

y \in [0, 1]

is given by

x = ϕ (y) = \frac{1}{ξ} \sinh (c_{2} y + c_{1} (1 - y)) + k,

()

where

ξ

is the stretching parameter,

c_{1} = \sinh^{- 1} (ξ (x_{\min} - k))

c_{2} = \sinh^{- 1} (ξ (x_{\max} - k))

and k is the stretched coordinate (which for our problem is

k = 0

that is, near the zero accumulated wealth). Using the transformed variable

V (y, t) = v (x, t)

, the Equations (1)–(5) can be rewritten as,

\begin{align} \frac{\partial V}{\partial t} + 𝔸 (y, u^{*}) \frac{\partial V}{\partial y} + 𝔹 (y, u^{*}) \frac{\partial^{2} V}{\partial y^{2}} = γ V, \end{align}

()

\begin{align} u^{*} (y, t) = sign (ℙ (y) \frac{\partial V}{\partial y} - ℚ (y) \frac{\partial^{2} V}{\partial y^{2}}), \end{align}

()

\begin{align} V (0, t) & = 0, \end{align}

()

\begin{align} V_{y} (1, t) & = J (1) e^{- r (T - t)}, \end{align}

()

\begin{align} V (y, T) & = \max (ϕ (y), 0) . \end{align}

()

with

\begin{align} J (y) & = \frac{\partial ϕ}{\partial y} = \frac{c_{2} - c_{1}}{ξ} \cosh (c_{2} y + c_{1} (1 - y)), \end{align}

()

\begin{align} H (y) & = \frac{\partial^{2} ϕ}{\partial y^{2}} = \frac{{(c_{2} - c_{1})}^{2}}{ξ} \sinh (c_{2} y + c_{1} (1 - y)), \end{align}

()

\begin{align} 𝔸 (y, u^{*}) & = \frac{(u^{*} - ϕ (y)) (r - γ)}{J (y)} - \frac{1}{2} {(u^{*} - ϕ (y))}^{2} σ^{2} \frac{H (y)}{{(J (y))}^{3}}, \end{align}

()

\begin{align} 𝔹 (y, u^{*}) & = \frac{1}{2} \frac{{(u^{*} - ϕ (y))}^{2} σ^{2}}{{(J (y))}^{2}}, \end{align}

()

\begin{align} ℙ (y) & = \frac{(r - γ)}{J (y)} + \frac{σ^{2} ϕ (y) H (y)}{{(J (y))}^{3}}, \end{align}

()

\begin{align} ℚ (y) & = \frac{σ^{2} ϕ (y)}{{(J (y))}^{2}} . \end{align}

()

In order to discretize (34) and (35) over the transformed domain

[0, 1]

, we use

Δ y = \frac{1}{M - 1}, y_{j} = (j - 1) Δ y, 1 \leq j \leq M

with

Δ t

being the same as previously defined. The time discretization of (34) using the CNIM is as follows,

\begin{align} \frac{V_{j}^{m + 1} - V_{j}^{m}}{Δ t} + 𝔸 (y_{j}, {(u^{*})}_{j}^{m + 1}) [\frac{{(V_{y})}_{j}^{m + 1} + {(V_{y})}_{j}^{m}}{2}] \\ + 𝔹 (y_{j}, {(u^{*})}_{j}^{m + 1}) [\frac{{(V_{y y})}_{j}^{m + 1} + {(V_{y y})}_{j}^{m}}{2}] = γ [\frac{V_{j}^{m + 1} + V_{j}^{m}}{2}] . \end{align}

()

The fourth order approximation to

V_{y}

and

V_{y y}

(similar to that of

v_{x}

and

v_{x x}

) are as follows,

\begin{align} {({\vec{V}}_{y y})}^{m} & = \frac{2}{{(Δ y)}^{2}} A^{- 1} B {(\vec{V})}^{m} + A^{- 1} {(\vec{C_{g s}})}^{m} . \end{align}

()

\begin{align} {({\vec{V}}_{y})}^{m} & = \frac{1}{Δ y} D^{- 1} E {(\vec{V})}^{m} + D^{- 1} {(\vec{F_{g s}})}^{m}, \end{align}

()

where the matrices A,

B, D

, E are same as given in (20), (21) and

{(\vec{C_{g s}})}^{m} = {(\frac{19}{24 {(Δ y)}^{2}} V_{1}^{m}, 0, \dots, 0, \frac{12}{Δ y} {(V_{y})}_{M}^{m})}^{T}, {(\vec{F_{g s}})}^{m} = {(- \frac{1}{Δ y} V_{1}^{m}, 0, \dots, 0, {(V_{y})}_{M}^{m})}^{T} .

Using (46) and (47), Equation (45) can be written as,

\begin{align} \frac{{(\vec{V})}^{m + 1} - {(\vec{V})}^{m}}{Δ t} + \frac{1}{2 Δ y} 𝕊^{m + 1} D^{- 1} E [{(\vec{V})}^{m + 1} + {(\vec{V})}^{m}] + \frac{1}{2} 𝕊^{m + 1} D^{- 1} [{(\vec{F_{g s}})}^{m + 1} + {(\vec{F_{g s}})}^{m}] \\ + \frac{1}{{(Δ y)}^{2}} ℝ^{m + 1} A^{- 1} B [{(\vec{V})}^{m + 1} + {(\vec{V})}^{m}] + \frac{1}{2} ℝ^{m + 1} A^{- 1} [{(\vec{C_{g s}})}^{m + 1} + {(\vec{C_{g s}})}^{m})] = \frac{γ}{2} [{(\vec{V})}^{m + 1} + {(\vec{V})}^{m})], \end{align}

()

where

ℝ

and

𝕊

are diagonal matrices given by

\begin{align} 𝕊^{m + 1} & = diag (α_{2}^{m + 1}, α_{3}^{m + 1}, \dots, α_{M - 1}^{m + 1}), α_{j}^{m + 1} = 𝔸 (y_{j}, {(u^{*})}_{j}^{m + 1}), \\ ℝ^{m + 1} & = diag (β_{2}^{m + 1}, β_{3}^{m + 1}, \dots, β_{M - 1}^{m + 1}), β_{j}^{m + 1} = 𝔹 (y_{j}, {(u^{*})}_{j}^{m + 1}) . \end{align}

()

Upon further simplification, (48) becomes

\begin{align} [(1 + \frac{γ Δ t}{2}) I - \frac{1}{2} q_{1} 𝕊^{m + 1} D^{- 1} E - p_{1} ℝ^{m + 1} A^{- 1} B] {(\vec{V})}^{m} \\ = [(1 - \frac{γ Δ t}{2}) I + \frac{1}{2} q_{1} 𝕊^{m + 1} D^{- 1} E + p_{1} ℝ^{m + 1} A^{- 1} B] {(\vec{V})}^{m + 1} \\ + \frac{Δ t}{2} 𝕊^{m + 1} D^{- 1} [{(\vec{F_{g s}})}^{m + 1} + {(\vec{F_{g s}})}^{m}] + \frac{Δ t}{2} ℝ^{m + 1} A^{- 1} [{(\vec{C_{g s}})}^{m + 1} + {(\vec{C_{g s}})}^{m})], \end{align}

()

where I is the identity matrix of size

(M - 2) \times (M - 2)

p_{1} = \frac{Δ t}{{(Δ y)}^{2}}

and

q_{1} = \frac{Δ t}{Δ y}

The discretization of

u^{*} (y, t)

using HOC is as follows

{(u^{*})}_{j}^{m} = sign (\frac{1}{2} ℙ (y_{j}) [{(V_{y})}_{j}^{m + 1} + {(V_{y})}_{j}^{m}] - \frac{1}{2} ℚ (y_{j}) [{(V_{y y})}_{j}^{m + 1} + {(V_{y y})}_{j}^{m}]),

()

which upon further simplification, by using (47) and (46) results in

\begin{align} {\vec{(u^{*})}}^{m} & = sign ([\frac{𝒫 D^{- 1} E}{2 Δ y} - \frac{𝒬 A^{- 1} B}{{(Δ y)}^{2}}] [{(\vec{V})}^{m + 1} + {(\vec{V})}^{m}] \\ + \frac{1}{2} 𝒫 D^{- 1} [{(\vec{F_{g s}})}^{m + 1} + {(\vec{F_{g s}})}^{m}] - \frac{1}{2} 𝒬 A^{- 1} [{(\vec{C_{g s}})}^{m + 1} + {(\vec{C_{g s}})}^{m})]) . \end{align}

()

where

{\vec{(u^{*})}}^{m} = {({(u^{*})}_{2}^{m}, \dots, {(u^{*})}_{M - 1}^{m})}^{⊤},

and

𝒫

and

𝒬

are diagonal matrices given by

\begin{align} 𝒫 & = diag (ℙ (y_{2}), ℙ (y_{3}), \dots, ℙ (y_{M - 1})) . \\ 𝒬 & = diag (ℚ (y_{2}), ℚ (y_{3}), \dots, ℚ (y_{M - 1})) . \end{align}

The price of an American passport option,

\hat{v} (x, t)

satisfies (1) and (2) on the continuation region denoted by

ℛ^{c}

, where

ℛ^{c} = \{(x, t) \in ℝ \times [0, T) : \hat{v} (x, t) > \max (x, 0)\}

, subject to the free boundary condition and terminal condition,

\hat{v} (x, t) \geq \max (x, 0), \forall (x, t)

()

and

\hat{v} (x, T) = \max (x, 0) .

()

In order to determine the value of the American passport option numerically, the following early exercise condition³

{\hat{v}}_{i, j} = \max (v_{i, j}, \max (x, 0)),

()

where

v_{i, j}

is the solution of (29) and (50) in case of and HOC and HOCGS schemes, respectively, is used.

4 NUMERICAL RESULTS

We now present the numerical results of the HOC and the HOCGS schemes obtained in Sections 2 and 3, respectively. A comparison of results using both the schemes along with the CNIM is presented, to illustrate the advantage of the application of HOC over CNIM with even more improved results that follow from the application of the HOCGS schemes.

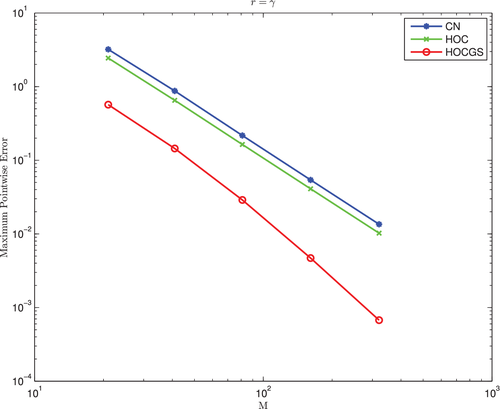
We begin with the symmetric case of $r = γ$ where we have the advantage of comparing the results with the analytic solution. The parameters used for the simulations (carried out in MatLab^TM) were the same that were used in the CNIM implementation carried out in Reference 3, that is, $S (t) = 100$ , $r = 0$ , $γ = 0$ , $σ = 30 %$ , and $T - t = 1$ . The simulations were carried out for several values of M and N. However, the tabulated results presented here are only for $M = 800$ and $N = 800$ . The prices for the symmetric case are tabulated in Table 1. We observe that the HOC scheme gives slightly better results as compared to the CNIM scheme. The inclusion of grid stretching through the HOCGS scheme further improves the results by giving values that closely match the analytic values. To further observe these improvements, the loglog plot of the maximum error against the number of spatial steps (M) for all the schemes are given in Figure 1. Note that this comparison was not restricted to only $M = 800$ , but for several values of M, namely M = 21, 41, 81, 161, and 321. It is clear that there is a marginal reduction in maximum error for the HOC scheme, but significant reduction if HOCGS scheme is used. The maximum error, the rate of convergence, and the CPU time for all the three schemes are tabulated in Table 2. We observe that both CNIM and HOC achieve only second order convergence while the HOCGS achieves close to third order convergence. While the convergence achieved through numerical implementation using HOCGS is unable to achieve fourth order accuracy, one does achieve better accuracy as compared to the CNIM scheme.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Loglog plot of maximum error against M for the European passport option with $S (t) = 100$ , $r = 0$ , $γ = 0$ , $σ = 30 %$ , $T - t = 1$ , and $N = 800$ with $ξ = 13$

TABLE 1. Price of the European passport option with

S (t) = 100

r = 0

γ = 0

σ = 30 %

T - t = 1

M = 800

, and

N = 800

with

ξ = 13

w	Analytic	CNIM	HOC	HOCGS
$-$ 20	5.887568	5.886553	5.886658	5.887572
$-$ 10	8.880836	8.879288	8.879603	8.880844
$-$ 5	10.830686	10.828835	10.829259	10.830680
$-$ 2	12.169565	12.168752	12.169237	12.169553
$-$ 1	12.646019	12.644768	12.645272	12.646016
0	13.138099	13.135937	13.136459	13.138079
1	13.646019	13.644768	13.645272	13.646016
2	14.169565	14.168752	14.169237	14.169553
5	15.830686	15.828835	15.829259	15.830680
10	18.880836	18.879288	18.879603	18.880844
20	25.887568	25.886553	25.886658	25.887572

TABLE 2. Maximum error, rate of convergence and CPU time for the European passport option with

S (t) = 100

r = 0

γ = 0

σ = 30 %

T - t = 1

, and

N = 800

with

ξ = 13

Spatial nodes	21	41	81	161	321
CNIM error	3.203367	0.873704	0.216691	0.054095	0.013519
CNIM order	-	1.874372	2.011507	2.002059	2.000502
CPU time (s)	0.050000	0.050000	0.150000	0.360000	1.370000
HOC error	2.442399	0.651655	0.163756	0.040994	0.010252
HOC order	-	1.906119	1.992564	1.998047	1.999559
CPU time (s)	0.080000	0.360000	0.860000	4.020000	171.6900
HOCGS error	0.568289	0.144473	0.028900	0.004692	0.000673
HOCGS order	-	1.975826	2.321656	2.622644	2.800841
CPU time (s)	0.100000	0.510000	1.200000	6.770000	51.68000

Prior to implementation of the nonsymmetric case of

r \neq γ

(for which there is no analytic solution) it is necessary to specify the method of calculation of maximum error and the rate of convergence in this case. Accordingly, the maximum error and rate of convergence is computed using the double-mesh principle.²⁹ Let

U^{M} (x_{i})

and

U^{2 M} (x_{i})

be the approximate numerical solutions (in the computational domain

[x_{\min}, x_{\max}]

) obtained with M and

2 M

mesh intervals, respectively. Also let

{\overline{Ω}}^{M} = \{x_{i} : x_{i} = x_{\min} + (i - 1) h, 1 \leq i \leq M\} .

where

h = \frac{x_{\max} - x_{\min}}{M - 1}

. The maximum error and the rate of convergence are determined by the double-mesh differences

E^{M} = \max_{x_{i} \in {\overline{Ω}}^{M}} | U^{M} (x_{i}) - U^{2 M} (x_{i}) |,

()

and

q = \log_{2} (\frac{E^{M}}{E^{2 M}}) .

()

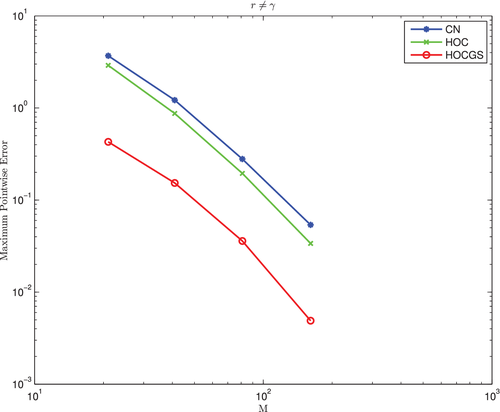
The numerical values of the European and American passport option for the nonsymmetric case, using all the three schemes are tabulated (for various accumulated gains) in Tables 3 and 4, respectively, with the parameters being taken to be $S (t) = 100$ , $r = 5 %$ , $γ = 4.5 %$ , $σ = 30 %$ , and $T - t = 2$ .³ The loglog plot of the maximum error against various spatial steps, as given by (56) are presented in Figure 2. Finally, the maximum error, the rate of convergence and the CPU time for the nonsymmetric case using the CNIM, HOC and HOCGS are given in Tables 5 and 6, respectively.

TABLE 3. Price of the European passport option with

S (t) = 100

r = 5 %

γ = 4.5 %

σ = 30 %

T - t = 2

M = 800

, and

N = 800

with

ξ = 13

w	CNIM	HOC	HOCGS
$-$ 20	10.428911	10.430595	10.430803
$-$ 10	13.509960	13.512246	13.512163
$-$ 5	15.357743	15.360405	15.360103
$-$ 2	16.577444	16.580551	16.579883
$-$ 1	17.003622	17.006314	17.006092
0	17.439919	17.440792	17.442332
1	17.886523	17.889334	17.889046
2	18.343627	18.347030	18.346170
5	19.778782	19.781776	19.781271
10	22.372380	22.374982	22.374694
20	28.226310	28.228299	28.228294

TABLE 4. Price of the American passport option with

S (t) = 100

r = 5 %

γ = 4.5 %

σ = 30 %

T - t = 2

M = 800

, and

N = 800

with

ξ = 13

w	CNIM	HOC	HOCGS
$-$ 20	10.612413	10.614219	10.613976
$-$ 10	13.787373	13.789847	13.789170
$-$ 5	15.700414	15.703318	15.702323
$-$ 2	16.967035	16.970438	16.968990
$-$ 1	17.410351	17.413314	17.412324
0	17.864595	17.865597	17.866500
1	18.330000	18.333108	18.332004
2	18.806809	18.810562	18.808815
5	20.306628	20.309958	20.308561
10	23.027069	23.030020	23.028786
20	28.551988	29.213696	29.212595

TABLE 5. Maximum error, rate of convergence and CPU time for the European passport option with

S (t) = 100

r = 5 %

γ = 4.5 %

σ = 30 %

T - t = 2

, and

N = 800

with

ξ = 13

Spatial nodes	21	41	81	161
CNIM error	3.692374	1.218312	0.279163	0.053758
CNIM order	-	1.599666	2.125705	2.376550
CPU time (s)	0.090000	0.090000	0.310000	0.450000
HOC error	2.904958	0.871569	0.194817	0.033796
HOC order	-	1.736830	2.161497	2.527194
CPU time (s)	0.290000	1.830000	4.480000	28.59000
HOCGS error	0.429031	0.153247	0.035894	0.004895
HOCGS order	-	1.485222	2.094036	2.874414
CPU time (s)	0.320000	2.210000	5.850000	38.76000

TABLE 6. Maximum error, rate of convergence and CPU time for the American passport option with

S (t) = 100

r = 5 %

γ = 4.5 %

σ = 30 %

T - t = 2

, and

N = 800

with

ξ = 13

Spatial nodes	21	41	81	161
CNIM error	3.692747	1.238479	0.284755	0.054978
CNIM order	-	1.576126	2.120778	2.372786
CPU time (s)	0.090000	0.090000	0.460000	0.540000
HOC error	2.864784	0.859610	0.186518	0.029594
HOC order	-	1.736673	2.204366	2.655934
CPU time (s)	0.270000	1.760000	4.500000	27.99000
HOCGS error	0.003617	0.004003	0.000790	0.000110
HOCGS ORDER	-	−0.146441	2.341362	2.841505
CPU time (s)	0.330000	2.050000	5.820000	36.82000

In order to observe the maximum error and rate of convergence with respect to grid stretching parameter $ξ$ , we present the numerical results for both the symmetric and nonsymmetric case, for several grid stretching parameters $ξ$ , in Tables 7 and 8, respectively, for various number of spatial steps.

TABLE 7. Maximum error and rate of convergence of the European passport option for various values of

ξ

and M, with

S (t) = 100

r = 0 %

γ = 0 %

σ = 30 %

T - t = 1

, and

N = 800

$ξ$	M=21	M=41	M=81	M=161	M=321
1	0.858980	0.217465	0.054529	0.013642	0.003411
	1.981842	1.995687	1.998968	1.999916
2	0.393637	0.099603	0.024972	0.006247	0.001562
	1.982607	1.995885	1.999085	2.000152
3	0.262586	0.059071	0.014811	0.003705	0.000926
	2.152258	1.995776	1.999125	2.000421
4	0.316357	0.072677	0.013157	0.002502	0.000625
	2.121981	2.465625	2.394758	2.000752
5	0.360326	0.084606	0.015630	0.002408	0.000456
	2.090476	2.436402	2.698680	2.400214
6	0.397625	0.094951	0.017826	0.002774	0.000391
	2.066148	2.413170	2.684078	2.827118
7	0.430080	0.104107	0.019807	0.003108	0.000439
	2.046534	2.394007	2.671740	2.822355
8	0.458848	0.112334	0.021614	0.003417	0.000485
	2.030222	2.377773	2.661075	2.817996
9	0.484714	0.119814	0.023278	0.003704	0.000527
	2.016338	2.363740	2.651695	2.814002
10	0.508230	0.126679	0.024823	0.003973	0.000566
	2.004303	2.351414	2.643332	2.810328
11	0.529804	0.133029	0.026266	0.004226	0.000604
	1.993717	2.340450	2.635792	2.806933
12	0.549744	0.138940	0.027622	0.004465	0.000639
	1.984296	2.330594	2.628933	2.803781
13	0.568289	0.144473	0.028900	0.004692	0.000673
	1.975826	2.321656	2.622644	2.800841
14	0.585628	0.149675	0.030111	0.004909	0.000706
	1.968147	2.313491	2.616842	2.798089
15	0.601915	0.154587	0.031261	0.005115	0.000737
	1.961136	2.305983	2.611457	2.795503

TABLE 8. Maximum error and rate of convergence of the European passport option for various values of

ξ

and M, with

S (t) = 100

r = 5 %

γ = 4.5 %

σ = 30 %

T - t = 2

, and

N = 800

$ξ$	M=21	M=41	M=81	M=161
1	0.658137	0.143690	0.026107	0.006971
	2.195429	2.460436	1.905090
2	0.252002	0.059186	0.014014	0.003056
	2.090101	2.078355	2.197110
3	0.269837	0.077166	0.013052	0.002396
	1.806046	2.563666	2.445724
4	0.303693	0.090864	0.016459	0.002862
	1.740837	2.464800	2.523634
5	0.329496	0.101962	0.019449	0.003191
	1.692228	2.390271	2.607718
6	0.349808	0.111354	0.022124	0.003498
	1.651409	2.331468	2.661031
7	0.366531	0.119434	0.024553	0.003767
	1.617722	2.282261	2.704571
8	0.380658	0.126579	0.026782	0.003973
	1.588455	2.240695	2.753014
9	0.393092	0.132907	0.028847	0.004180
	1.564453	2.203930	2.786737
10	0.403794	0.138755	0.030772	0.004379
	1.541075	2.172835	2.812973
11	0.413034	0.143960	0.032579	0.004546
	1.520596	2.143658	2.841175
12	0.421538	0.148877	0.034282	0.004724
	1.501543	2.118600	2.859329
13	0.429031	0.153247	0.035894	0.004895
	1.485222	2.094036	2.874414
14	0.436074	0.157517	0.037426	0.004989
	1.469064	2.073388	2.907113
15	0.442243	0.161376	0.038886	0.005182
	1.454413	2.053086	2.907717

5 CONCLUSION

We consider the problem of pricing the passport option for both the symmetric case as well as the nonsymmetric case through HOC schemes in order to obtain better results on a compact stencil. The HOC scheme applied on the nonlinear pricing PDE with non-smooth coefficients resulted in improved results as compared to the CNIM, for the symmetric case with known pricing formula. However, the advantage of the HOC schemes turned out to be much more significant with close to third order accuracy being achieved with the introduction of grid stretching near the zero accumulated wealth level. In fact, the results obtained through grid stretching show a very close match for the analytic solution for the symmetric case. Further, it was observed that the maximum error was also significantly reduced with the introduction of grid stretching. Similar results with regards to accuracy and maximum error was observed for the nonsymmetric case also, using the double-mesh differences for the error.

ACKNOWLEDGMENTS

The first author is grateful to Indian Institute of Technology Guwahati for the Assistantship provided to pursue his Ph.D. The authors express their gratitude to both the Referees for their comments and suggestions.

CONFLICT OF INTEREST

This work does not have any conflicts of interest.

Biographies

Ankur Kanaujiya has been a faculty at the National Institute of Technology Rourkela, since 2020. He earned a doctorate degree in Mathematics from the Indian Institute of Technology Guwahati. His area of interest is Computational Finance. He has worked as assistant professor under Technical Education Quality Improvement Programme (TEQIP-III), a World Bank assisted project implemented by the National Project Implementation Unit (NPIU), at Birla Institute of Technology Mesra, Ranchi.
Siddhartha P. Chakrabarty is a professor in Mathematics and Data Science & Artificial Intelligence at the Indian Institute of Technology Guwahati. His research areas include Mathematical Finance and Mathematical Biology. He has supervised more than 40 students, including 4 Ph.D. students and is a recipient of several grants and awards, he is actively involved in service and outreach activities, including organizing professional events. His diverse teaching experience includes MOOC courses.

REFERENCES

1Hyer T, Lipton-Lifschitz A, Pugachevsky D. Passport to success. Risk. 1997; 10(9): 127-131.
Google Scholar
2Topper J. A Finite Element Implementation of Passport Options. M.Sc. thesis. University of Oxford; 2003.
Google Scholar
3Andersen L, Andreasen J, Brotherton-Ratcliffe R. The passport option. J Comput Finance. 1998; 1(3): 15-36.
10.21314/JCF.1998.013
Google Scholar
4Nagayama I. Pricing of passport option. J Math Sci Univ Tokyo. 1998; 5(4): 747-785.
Google Scholar
5Ahn H, Penaud A, Wilmott P. Various passport options and their valuation. Appl Math Finance. 1999; 6(4): 275-292.
10.1080/13504869950079293
Google Scholar
6Chan SS. The valuation of American passport options. Working paper. University of Wisconsin-Madison; 1999.
Google Scholar
7Penaud A, Wilmott P, Ahn H. Exotic passport options. Asia-Pac Financ Markets. 1999; 6(2): 171-182.
10.1023/A:1010093029306
Google Scholar
8Henderson V, Hobson D. Local time, coupling and the passport option. Finance Stoch. 2000; 4(1): 69-80.
10.1007/s007800050003
Google Scholar
9Shreve SE, Vecer J. Options on a traded account: vacation calls, vacation puts and passport options. Finance Stoch. 2000; 4(3): 255-274.
10.1007/s007800050073
Google Scholar
10Henderson V, Hobson D. Passport options with stochastic volatility. Appl Math Finance. 2001; 8(2): 97-118.
10.1080/13504860110068863
Google Scholar
11Baojun B, Yang W. A viscosity solution approach to valuation of passport options in a jump-diffusion model. Proceedings of the 27th Chinese Control Conference; 2008:606-608; Kunming, Yunnan, China.
Google Scholar
12Kampen J. Optimal strategies of passport options. Math Ind. 2008; 12: 666-670.
10.1007/978-3-540-71992-2_110
Google Scholar
13Baojun B, Yang W, Jizhou Z. Viscosity solutions of HJB equations arising from the valuation of European passport options. Acta Math Sci. 2010; 30(1): 187-202.
10.1016/S0252-9602(10)60036-7
Web of Science® Google Scholar
14Malloch H, Buchen PW. Passport option: continuous and binomial models. Proceedings of the Finance and Corporate Governance Conference; 2011.
Google Scholar
15Delbaen F, Yor M. Passport options. Math Financ. 2002; 12(4): 299-328.
10.1111/j.1467-9965.2002.tb00126.x
Web of Science® Google Scholar
16Kanaujiya A, Chakrabarty SP. Pricing European passport option with radial basis function. Int J Appl Comput Math. 2017; 3(3): 1589-1604.
10.1007/s40819-016-0240-1
Google Scholar
17Kanaujiya A, Chakrabarty SP. Pricing and estimates of Greeks for passport option: a three time level approach. J Comput Appl Math. 2017; 315: 49-64.
10.1016/j.cam.2016.10.027
Web of Science® Google Scholar
18Kanaujiya A, Chakrabarty SP. Valuation of American passport option using a three time level scheme. Comput Appl Math. 2019; 38:30.
10.1007/s40314-019-0785-9
Web of Science® Google Scholar
19Spotz WF, Carey GF. High-order compact finite difference methods. Proceedings International Conference on Spectral and High Order Methods; 1995:397-408; Houston, TX.
Google Scholar
20Kalita JC, Dalal DC, Dass AK. A class of higher order compact schemes for the unsteady two-dimensional convection-diffusion equation with variable convection coefficients. Int J Numer Methods Fluids. 2002; 38(12): 1111-1131.
10.1002/fld.263
CAS Web of Science® Google Scholar
21Karaa S, Zhang J. High order ADI method for solving unsteady convection-diffusion problems. J Comput Phys. 2004; 198(1): 1-9.
10.1016/j.jcp.2004.01.002
Web of Science® Google Scholar
22Zhao J, Dai W, Niu T. Fourth-order compact schemes of a heat conduction problem with Neumann boundary conditions. Numer Methods Part Differ Equ. 2007; 23(5): 949-959.
10.1002/num.20200
Web of Science® Google Scholar
23Yambangwai D, Moshkin N. Deferred correction technique to construct high-order schemes for the heat equation with Dirichlet and Neumann boundary conditions. Eng Lett. 2013; 21(2): 61-67.
Google Scholar
24Tangman DY, Gopaul A, Bhuruth M. Numerical pricing of options using high-order compact finite difference schemes. J Comput Appl Math. 2008; 218(2): 270-280.
10.1016/j.cam.2007.01.035
Web of Science® Google Scholar
25Oosterlee CW, Leentvaar CCW, Huang X. Accurate American option pricing by grid stretching and high order finite differences. Technical report Delft University of Technology, The Netherlands; 2005.
Google Scholar
26Lele SK. Compact finite difference schemes with spectral-like resolution. J Comput Phys. 1992; 103(1): 16-42.
10.1016/0021-9991(92)90324-R
Web of Science® Google Scholar
27Collatz L. The Numerical Treatment of Differential Equations. Springer; 1966.
Google Scholar
28Atkinson KE. An Introduction to Numerical Analysis. John Wiley & Sons; 1988.
Google Scholar
29Bawa RK, Natesan S. An efficient hybrid numerical scheme for convection-dominated boundary-value problems. Int J Comput Math. 2009; 86(2): 261-273.
10.1080/00207160801955678
Web of Science® Google Scholar

All articles

Pricing passport option using higher order compact scheme

Abstract

1 INTRODUCTION

2 THE HIGHER ORDER COMPACT SCHEMES

2.1 The interior points

2.2 The boundary points

3 GRID STRETCHING

4 NUMERICAL RESULTS

5 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST

Biographies

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Pricing passport option using higher order compact scheme

Abstract

1 INTRODUCTION

2 THE HIGHER ORDER COMPACT SCHEMES

2.1 The interior points

2.2 The boundary points

3 GRID STRETCHING

4 NUMERICAL RESULTS

5 CONCLUSION

ACKNOWLEDGMENTS

CONFLICT OF INTEREST

Biographies

REFERENCES

Figures

References

Related

Information