SPECIAL ISSUE PAPER

Full Access

An asymptotic streamline diffusion finite element method for singularly perturbed convection-diffusion delay differential equations with point source

Senthilkumar Sethurathinam

Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur, India

Search for more papers by this author

Subburayan Veerasamy,

Corresponding Author

Subburayan Veerasamy

[email protected]

Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur, India

Correspondence Veerasamy Subburayan, Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur 603 203, Tamilnadu, India.

Email: [email protected]

Search for more papers by this author

Rameshbabu Arasamudi,

Rameshbabu Arasamudi

Department of Mathematics, School of Engineering, Amrita Vishwa Vidyapeetham, Coimbatore, India

Search for more papers by this author

Ravi P. Agarwal,

Ravi P. Agarwal

Department of Mathematics, Texas A&M University-Kingsville, Kingsville, Texas, USA

Search for more papers by this author

Senthilkumar Sethurathinam,

Senthilkumar Sethurathinam

Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur, India

Search for more papers by this author

Subburayan Veerasamy,

Corresponding Author

Subburayan Veerasamy

[email protected]

Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur, India

Correspondence Veerasamy Subburayan, Department of Mathematics, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur 603 203, Tamilnadu, India.

Email: [email protected]

Search for more papers by this author

Rameshbabu Arasamudi,

Rameshbabu Arasamudi

Department of Mathematics, School of Engineering, Amrita Vishwa Vidyapeetham, Coimbatore, India

Search for more papers by this author

Ravi P. Agarwal,

Ravi P. Agarwal

Department of Mathematics, Texas A&M University-Kingsville, Kingsville, Texas, USA

Search for more papers by this author

First published: 08 October 2021

https://doi.org/10.1002/cmm4.1201

Citations: 3

SDFEM for delay equations.

Share a link

Email
Wechat
Bluesky

Abstract

In this article, we presented an asymptotic SDFEM for singularly perturbed convection diffusion type differential difference equations with point source term. First, the solution is decomposed into two functions, among them one is the solution of delay differential equation and other one is the solution of differential equation with point source. Furthermore, using the asymptotic expansion approximation, the delay differential equation is modified as a nondelay differential equations. Streamline diffusion finite element methods are applied to approximate the solutions of the two problems. We prove that the present method gives an almost second-order convergence in maximum norm and square integrable norm, whereas first-order convergence in $H^{1}$ norm. Numerical results are presented to validate the theoretical results.

1 INTRODUCTION

Singularly perturbed differential equations play a vital role in several branches of applied science. A subclass is a singularly perturbed delay differential equation (SPDDE) in which, the equation involves at least one delay argument. Plenty of research articles have appeared in the literature which cover second- and higher-order equations. Not much work has been done in finite element method (FEM) and streamline diffusion finite element method (SDFEM) for those problems. Authors in Reference 1 discussed finite element discretization on general adopted meshes. Zarin² developed discontinuous Galerkin FEM for SPDDE on Shishkin mesh. A robust exponential convergence rate for hp version of the finite element method on an appropriately designed mesh is obtained in Reference 3. A numerical method based on finite element is developed in Reference 4 to solve singularly perturbed system of convection-diffusion delay differential equations. In general, the Galerkin FEM on the layer adapted mesh will not give satisfactory results for second-order equations because of stability issues. In Reference 5 Roos and Zarin proposed an SDFEM to tackle the problem arised due to the stability for nondelayed equations, whereas the stability and accuracy of SDFEM for SPDDE is discussed in Reference 6. An SDFEM for second-order singularly perturbed differential equations with discontinuous source term is suggested in Reference 7. Becher⁸ obtained uniform error estimates of the SDFEM for a turning point problem in the SD-norm. Chen and Xu⁹ proved the stability and accuracy of FEM and SDFEM for singularly perturbed problems. On the other side, the research on the higher-order finite difference methods is considerably increased compared to FEM and SDFEM.^10-12 Many authors suggested various types of finite difference schemes for solving the same type of equations. An asymptotic numerical method for singularly perturbed convection-diffusion problems with a negative shift is suggested by Subburayan and Ramanujam.¹³ Authors in Reference 14 proposed a second-order hybrid finite difference scheme for singularly perturbed convection-diffusion problems with a negative shift. In Reference 15, authors coined a second-order uniformly convergent central difference scheme for the numerical solution of a system of coupled reaction-diffusion equations. In recent years, many authors proposed several types of adaptive mesh analysis and its convergent analysis for delay and nondelay differential equations, to cite a very few: References 16-27.

As mentioned in the abstract, the solution is decomposed into two functions, among them one is the solution of delay differential equation and other one is the solution of differential equation with point source. Furthermore, the delayed term is replaced by an asymptotic expansion approximation. Streamline diffusion finite element methods are applied to approximate the solutions of the two problems. It is proved that the present method gives an almost second-order convergence in maximum norm and square integrable norm, whereas first-order convergence in $H^{1}$ norm.

2 PROBLEM STATEMENT

Consider the following boundary value problems (BVPs) for singularly perturbed delay differential equations (SPDDEs):^{28, 29}

Find

y \in Y : = C^{0} (\overline{Ω}) \cap C^{1} (Ω) \cap C^{2} (Ω^{*})

such that

P y (x) : = \{\begin{cases} - ε y^{''} (x) + a (x) y^{'} (x) + b (x) y (x) + c (x) y (x - 1) = δ (x - 1) + f (x), x \in Ω^{*}, \\ y (x) = 0, x \in [- 1, 0], y (2) = 0, \end{cases}

()

where

δ (x - 1) = \{\begin{cases} 1, if x = 1, \\ 0, if x \neq 1, \end{cases}

a (x) \geq α > 0,

b (x) \geq β > 0,

0 \geq γ_{1} \geq c (x) \geq γ_{0},

where

a, b,

and f are sufficiently differentiable functions on

\overline{Ω} .

Furthermore,

Ω = (0, 2)

be a set and its closure

\overline{Ω} = [0, 2]

and

Ω^{*} = Ω^{-} \cup Ω^{+},

Ω^{-} = (0, 1),

Ω^{+} = (1, 2)

and

ρ = b (x) - \frac{a^{'} (x)}{2} \geq 0 .

Let

y_{1} \in Y

and

y_{2} \in C^{0} (\overline{Ω}) \cap C^{2} (Ω)

be two functions such that

y (x) = y_{1} (x) + y_{2} (x)

. The functions

y_{1}

and

y_{2}

satisfy the following:

P_{1} y_{1} : = \{\begin{cases} - ε y_{1}^{''} (x) + a (x) y_{1}^{'} (x) + b (x) y_{1} (x) = δ (x - 1), x \in Ω^{*}, \\ y_{1} (0) = 0, y_{1} (2) = 0 \end{cases}

()

and

P_{2} y_{2} : = \{\begin{cases} - ε y_{2}^{''} (x) + a (x) y_{2}^{'} (x) + b (x) y_{2} (x) + c (x) y_{2} (x - 1) = f (x) - c (x) y_{1} (x - 1), x \in Ω, \\ y_{2} (x) = 0, x \in [- 1, 0], y_{2} (2) = 0 . \end{cases}

()

3 STABILITY AND ANALYTICAL RESULTS

This section presents the stability result of the solution of (3) and the derivative estimates of the solution components $y_{1}$ and $y_{2} .$

Lemma 1. ([14])Suppose that $ψ \in C^{0} (\overline{Ω}) \cap C^{2} (Ω^{*}),$ satisfies $ψ (0) \geq 0$ , $ψ (2) \geq 0$ , $P_{2} ψ (x) \geq 0, x \in Ω^{*}$ and $ψ^{'} (1 +) - ψ^{'} (1 -) \leq 0,$ then $ψ (x) \geq 0, x \in \overline{Ω}$ .

Lemma 2. ([14])If the function $ψ \in Y$ , then $| ψ (x) | \leq C \sup {| ψ (0) |, | ψ (2) |, \sup_{η \in Ω^{*}} | P_{2} ψ (η) |},$ $x \in \overline{Ω} .$

Lemma 3. ([29])Let $y_{1}$ be the solution of (2). The solution $y_{1}$ decomposed as $v_{1} + w_{1},$

$w_{1} = \{\begin{cases} w_{1, 1}, x \in Ω^{-}, \\ w_{1, 2}, x \in Ω^{+}, \end{cases}$ wherethe regular component function $v_{1}$ satisfies $P_{1} v_{1} = δ (x - 1), x \in Ω^{*}$ , the interior layer component function $w_{1, 1}$ satisfies $P_{1} w_{1, 1} = 0, x \in Ω^{-}$ and the boundary layer component function $w_{1, 2}$ satisfies $P_{1} w_{1, 2} = 0, x \in Ω^{+}$ . Then for $k = 0, 1, 2, 3$

\begin{align} | v_{1}^{(k)} (x) | & \leq C, x \in Ω^{*}, \\ | w_{1, 1}^{(k)} (x) | & \leq C ε^{- k} e^{- \frac{α}{ε} (1 - x)}, x \in Ω^{-}, | w_{1, 2}^{(k)} (x) | \leq C ε^{- k} e^{- \frac{α}{ε} (2 - x)}, x \in Ω^{+} . \end{align}

Lemma 4. ([30])Let $y_{2}$ be the solution of (3). The solution $y_{2}$ is decomposed as $v_{2} + w_{2},$ $w_{2} = \{\begin{cases} w_{2, 1}, x \in Ω^{-}, \\ w_{2, 2}, x \in Ω^{+}, \end{cases}$ where the regular component function $v_{2}$ satisfies $P_{2} v_{2} = f (x) - c (x) y_{1} (x - 1), x \in Ω^{*}$ , the interior layer component function $w_{2, 1}$ satisfies $P_{2} w_{2, 1} = 0, x \in Ω^{*}$ and the boundary layer component function $w_{2, 2}$ satisfies $P_{2} w_{2, 2} = 0, x \in Ω^{*}$ . Then for $k = 0, 1, 2, 3$

\begin{align} | v_{2}^{(k)} (x) | & \leq C, x \in Ω^{*}, \\ | w_{2, 1}^{(k)} (x) | & \leq C ε^{(1 - k)} e^{- \frac{α}{ε} (1 - x)}, x \in Ω^{-}, | w_{2, 2}^{(k)} (x) | \leq C ε^{- k} e^{- \frac{α}{ε} (2 - x)}, x \in Ω^{+} . \end{align}

4 ASYMPTOTIC EXPANSION APPROXIMATION

Let

y_{2, 0} \in C (\overline{Ω}) \cap C^{1} (0, 2]

and

y_{2, 1} \in C (\overline{Ω}) \cap C^{1} (Ω^{*} \cup {2})

be the solutions of the following:

\{\begin{cases} a (x) y_{2, 0}^{'} (x) + b (x) y_{2, 0} (x) + c (x) y_{2, 0} (x - 1) = f (x) - c (x) y_{1} (x - 1), x \in Ω, \\ y_{2, 0} (x) = 0, x \in [- 1, 0], \end{cases}

()

and

\{\begin{cases} a (x) y_{2, 1}^{'} (x) + b (x) y_{2, 1} (x) + c (x) y_{2, 1} (x - 1) = y_{2, 0}^{''} (x), x \in Ω^{*}, \\ y_{2, 1} (x) = 0, x \in [- 1, 0] . \end{cases}

()

An asymptotic expansion approximation (AEA) of the solution of Equation (3) is

y_{2, a s} (x) = \{\begin{cases} 0, & x \in [- 1, 0], \\ y_{2, 0} (x) + ε y_{2, 1} (x) + k_{1} (p_{1} (x) - p_{1} (0)), & x \in [0, 1], \\ y_{2, 0} (x) + ε y_{2, 1} (x) + k_{2} (p_{2} (x) - 1) - y_{2, 0} (2) - ε y_{2, 1} (2), & x \in [1, 2], \end{cases}

()

where

p_{1}

and

p_{2}

satisfy the following

ε p_{1}^{'} (x) - a (x) p_{1} (x) = 0, x \in [0, 1), p_{1} (1) = 1, ε p_{2}^{'} (x) - a (x) p_{2} (x) = 0, x \in [1, 2), p_{2} (2) = 1,

and the constants³¹

k_{1} = O (ε), k_{2} = O (1) .

Lemma 5. ([31])Let $y_{2}$ be the solution of (3) and $y_{2, a s}$ be its asymptotic approximation given by (6). Then, $| y_{2} (x) - y_{2, a s} (x) | \leq C ε^{2}, x \in \overline{Ω}$ .

Since

| y_{2} (x) - y_{2, a s} (x) | \leq C ε^{2}

, then the delayed term

y_{2} (x - 1)

can be replaced by

y_{2, a s} (x - 1)

in Equation (3). Therefore, we have the following modified problem

\begin{align} - & ε y_{2}^{*''} (x) + a (x) y_{2}^{*'} (x) + b (x) y_{2}^{*} (x) = g^{*} (x), x \in Ω, \\ y_{2}^{*} (0) = 0, y_{2}^{*} (2) = 0, \end{align}

()

where

g^{*} (x) = \{\begin{cases} f (x) - c (x) y_{1} (x - 1), x \in Ω^{-}, \\ f (x) - c (x) y_{1} (x - 1) - c (x) y_{2, a s} (x - 1), x \in Ω^{+} . \end{cases}

Lemma 6. ([31])Let $y_{2}$ and $y_{2}^{*}$ be the solutions of (3) and (7), respectively. Then, $| y_{2} (x) - y_{2}^{*} (x) | \leq C ε^{2}, x \in \overline{Ω}$ .

Proof.Using the results given in [32, section 2] and Reference 31, we prove the Lemma. Let $z (x) = y_{2} (x) - y_{2}^{*} (x)$ , then

L_{ε} z (x) = L_{ε} y_{2} (x) - L_{ε} y_{2}^{*} (x) = - c (x) y_{2} (x - 1) + f (x) - c (x) y_{1} (x - 1) - g^{*} (x) = \{\begin{cases} 0, & x \in Ω^{-}, \\ c (x) [y_{2, a s} (x - 1) - y_{2} (x - 1)], & x \in Ω^{+}, \end{cases}

where

L_{ε} = - ε \frac{d^{2}}{d x^{2}} + a (x) \frac{d}{d x} + b (x)

. Then by the above Lemma 5 and [ 32, lemma 2], we have the desired result.

5 WEAK FORMULATIONS

5.1 Weak formulation of the problem (2)

A weak formulation²⁹ of the above problem (2) is as follows: Find

y_{1} \in V = H_{0}^{1} (\overline{Ω})

such that

A (y_{1}, v) = v (1), \forall v \in V,

()

where

A (r, s) : = (ε r', s') + (a r^{'}, s) + (b r, s),

(r, s) = \int_{0}^{2} r s d x .

5.2 Weak formulation of the problem (7)

The weak formulation of (7) is as follows: Find

y_{2}^{*} \in V = H_{0}^{1} (\overline{Ω})

such that

A (y_{2}^{*}, v) = g (v), \forall v \in V,

()

where

g (v) = (g^{*}, v) .

Let us define finite dimensional space

V_{h}

V_{h} = {v \in H_{0}^{1} : v |_{I_{i}} \in P^{1} (I_{i}), \forall I_{i} \subset Ω, I_{i} = [x_{i - 1}, x_{i}]} .

Lemma 7. (coercive property[⁷])The functionals defined in (8) and (9) satisfy $A (y_{1}, y_{1}) \geq | | | y_{1} | | |_{V}^{2}$ and $A (y_{2}^{*}, y_{2}^{*}) \geq | | | y_{2}^{*} | | |_{V}^{2}$ , where $| | | χ | | |_{V}^{2} = ε | χ |_{1}^{2} + ρ ‖ χ ‖_{0}^{2}$ , $‖ χ ‖_{0}^{2} = (χ, χ)$ and $| χ |_{1} = ‖ χ^{'} ‖_{0}$ .

6 FINITE ELEMENT FORMULATIONS

6.1 Mesh points and properties

Let N be a positive integer and

λ = \min {\frac{1}{2}, \frac{ε τ_{0} \log N}{α}}

τ_{0} \geq 2

. Furthermore,

Ω_{ε}^{N} = {x_{i}}_{i = 0}^{N} .

The mesh will be equidistant on

Ω_{s},

where

Ω_{s} = (0, 1 - λ) \cup (1, 2 - λ)

and graded on

Ω_{0},

where

Ω_{0} = (1 - λ, 1) \cup (2 - λ, 2)

. We choose the transition points to be

x_{N / 4} = 1 - λ

x_{3 N / 4} = 2 - λ

. The mesh points are

x_{i} = \{\begin{cases} \frac{4 i (1 - λ)}{N}, & i = 0, \dots, N / 4, \\ 1 - \frac{τ_{0} ε}{α} ϕ (t_{i}), & i = N / 4 + 1, \dots, N / 2, \\ 1 + \frac{4 (1 - λ) (i - N / 2)}{N}, & i = N / 2 + 1, \dots, 3 N / 4, \\ 2 - \frac{τ_{0} ε}{α} ϕ (t_{i}), & i = 3 N / 4 + 1, \dots, N, \end{cases}

where

t_{i} = i N^{- 1},

ϕ = - \log (ψ)

and

ψ = e^{- 2 (1 - 2 t) \log N}

. On coarse part

Ω_{s},

we have

h_{i} \leq C N^{- 1},

where

h_{i} = x_{i} - x_{i - 1}

. It is obvious that on the layer part

Ω_{0}

of the Shishkin mesh,

h_{i} \leq C ε N^{- 1} \log N

.⁵

6.2 The streamline diffusion finite element method for (8)

A_{h} (y_{1 h}, v_{h}) = v_{h} (1), \forall v_{h} \in V_{h},

()

where

A_{h} (y_{1 h}, v_{h}) : = (ε y_{1 h}^{'}, v_{h}^{'}) + (a y_{1 h}^{'}, v_{h}) + (b y_{1 h}, v_{h}) + \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} δ_{k} (- ε y_{1 h}^{″} + a y_{1 h}^{'} + b y_{1 h}) a v_{h}^{'} .

Lemma 8. ([29])Let $y_{1}$ be the solution of the problem (2) and its interpolation be $y_{1}^{I}$ , then $| y_{1} (x) - y_{1}^{I} (x) | \leq C \{\begin{cases} {(N^{- 1} \max | ψ^{'} |)}^{2}, & x \in Ω_{0}, \\ N^{- 2}, & x \in Ω_{s} . \end{cases}$

Lemma 9. ([29])Let $y_{1}$ be the solution of the problem (2) and its numerical solution defined by (10), then $| y_{1} (x_{i}) - y_{1 h} (x_{i}) | \leq C N^{- 2}, x_{i} \in Ω_{ε}^{N} .$

Lemma 10. ([29])Let $y_{1}$ be the solution of the problem (2) and its numerical solution defined by (10), then $| | y_{1} - y_{1 h} | |_{0} \leq C N^{- 2}, x \in Ω_{ε}^{N} .$

6.3 The streamline diffusion finite element method for (9)

A_{h} (y_{2 h}^{*}, v_{h}) = (G^{*}, v_{h}) + \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} δ_{k} G^{*} a v_{h}^{'}, \forall v_{h} \in V_{h},

()

where

\begin{align} G^{*} & = f (x) - c (x) y_{1 h} (x - 1) - c (x) Y_{2, a s} (x - 1) = g^{*} (x) + c (x) [y_{1} (x - 1) - y_{1 h} (x - 1)] + c (x) [y_{2, a s} (x - 1) - Y_{2, a s} (x - 1)], \\ Y_{2, a s} & = \sum_{i = 0}^{N} ϕ_{i} (x) Y_{2, a s} (x_{i}), A_{h} (y_{2 h}^{*}, v_{h}) = (ε y_{2 h}^{*^{'}}, v_{h}^{'}) + (a y_{2 h}^{*^{'}}, v_{h}) + (b y_{2 h}^{*}, v_{h}) + \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} δ_{k} (- ε y_{2 h}^{*^{''}} + a y_{2 h}^{*^{'}} + b y_{2 h}^{*}) a v_{h}^{'} . \end{align}

Here we define a discrete energy norm on

V_{h}

associated with the bilinear form

A_{h} (*, *)

| | | y_{h}^{*} | | |_{V_{h}} : = {[ε | y_{h}^{*} |_{1}^{2} + ρ | | y_{h}^{*} | |_{0}^{2} + \sum_{i = 1}^{N} \int_{x_{i - 1}}^{x_{i}} δ_{i} a^{2} (x) {(y_{h}^{*})}^{^{'}})^{2} d x]}^{1 / 2}

. By Lax-Milgram theorem, we conclude that the problem has a unique solution. The corresponding difference scheme of (10) is

L^{N} y_{1, i} : = - ε (D^{+} y_{1, i} - D^{-} y_{1, i}) + α_{i} D^{+} y_{1, i} + β_{i} D^{-} y_{1, i} + γ_{i} y_{1, i} = ϕ_{i} (1), i = 1, \dots, N - 1,

where

\begin{align} D^{+} y_{1, i} = \frac{y_{1, i + 1} - y_{1, i}}{h_{i + 1}}, D^{-} y_{1, i} = \frac{y_{1, i} - y_{1, i - 1}}{h_{i}}, α_{i} = \frac{h_{i + 1} a (x_{i - 1 / 2})}{2} - δ_{i + 1} a^{2} (x_{i + 1 / 2}) \\ + \frac{h_{i + 1}^{2} b (x_{i + 1 / 2})}{4} - δ_{i + 1} h_{i + 1} a (x_{i + 1 / 2}) b (x_{i + 1 / 2}), \\ β_{i} = \frac{h_{i} a (x_{i - 1 / 2})}{2} - \frac{h_{i}^{2} b (x_{i - 1 / 2})}{4} + δ_{i} a^{2} (x_{i - 1 / 2}) - δ_{i} h_{i} a (x_{i - 1 / 2}) b (x_{i - 1 / 2}), \\ γ_{i} = \frac{h_{i} b (x_{i - / 2})}{2} + δ_{i} a (x_{i - 1 / 2}) b (x_{i - 1 / 2}) + \frac{h_{i + 1} b (x_{i + 1 / 2})}{2} - δ_{i + 1} a (x_{i + 1 / 2}) b (x_{i + 1 / 2}), x_{i - 1 / 2} = \frac{x_{i} + x_{i - 1}}{2}, x_{i + 1 / 2} = \frac{x_{i} + x_{i + 1}}{2} . \end{align}

Now we choose the parameter $δ_{i}$ as $δ_{i}$ = $\{\begin{cases} 0 & if h_{i} \leq \frac{2 ε}{| | a | |}, \\ \frac{\frac{h_{i}^{2} b (x_{i - 1 / 2})}{4} + \frac{h_{i} a (x_{i - 1 / 2})}{2}}{a^{2} (x_{i - 1 / 2}) + h_{i} a (x_{i - 1 / 2}) b (x_{i - 1 / 2})} & if h_{i} \geq \frac{2 ε}{| | a | |} . \end{cases}$

The corresponding difference scheme of (11) is

L^{N} y_{2, i}^{*} : = - ε (D^{+} y_{2, i}^{*} - D^{-} y_{2, i}^{*}) + α_{i} D^{+} y_{2, i}^{*} + β_{i} D^{-} y_{2, i}^{*} + γ_{i} y_{2, i}^{*} = G_{h}^{*} (ϕ_{i}), i = 1, \dots, N - 1,

where

D^{+} y_{2, i}^{*} = \frac{y_{2, i + 1}^{*} - y_{2, i}^{*}}{h_{i + 1}}, D^{-} y_{2, i}^{*} = \frac{y_{2, i}^{*} - y_{2, i - 1}^{*}}{h_{i}}, G_{h}^{*} (ϕ_{i}) = \sum_{k = 1}^{n} \int_{x_{k - 1}}^{x_{k}} δ_{k} G^{*} a ϕ_{i}^{'} .

7 ERROR ESTIMATES IN GENERAL SETUP

In this section, we estimate the interpolation error, projection error and consistency error based on the idea given in References 7, 29. Hence we prove that the method is consistent FEM, as the consistency error vanishes.

A general problem of the form $A (y_{2}^{*}, v) = g (v), \forall v \in V$ is discretized by:

find $y_{2 h}^{*} \in V_{h} \subset V$ such that $A_{h} (y_{2 h}^{*}, v_{h}) = G_{h}^{*} (v_{h}), \forall v_{h} \in V_{h} .$

The continuous problem has a unique solution $y_{2}^{*}$ and the nodal interpolation is well defined.

We define a biorthogonal basis of $V_{h}$ with respect to $A_{h}$ to be the set of functions ${λ^{j}}_{j = 0}^{N}$ which satisfy $A_{h} (ϕ_{i}, λ^{j}) = δ_{i j}, i = 0, \dots, N .$

The function $v_{h} \in V_{h}$ can be uniquely expressed as $v_{h} = \sum_{i = 0}^{N} A_{h} (v_{h}, λ^{i}) ϕ_{i}$ .

Define a projection operator²⁹ $P : V \to V_{h}$ such that $P v : = \sum_{i = 0}^{N} A_{h} (v, λ^{i}) ϕ_{i} .$

Furthermore, for a consistent method we have $P y_{2}^{*} = y_{2 h}^{*}$ . The error $y_{2}^{*} - y_{2 h}^{*}$ can be determined from the following $y_{2}^{*} - y_{2 h}^{*} = y_{2}^{*} - {(y_{2}^{*})}^{I} + P ({(y_{2}^{*})}^{I} - y_{2}^{*}) + P y^{*} - y_{2 h}^{*} .$

In a similar fashion, we can have $y_{1} - y_{1 h} = y_{1} - {(y_{1})}^{I} + P ({(y_{1})}^{I} - y_{1}) + P y_{1} - y_{1 h} .$

7.1 Interpolation error

Following the arguments of Reference 7 one can prove the error convergence.

Lemma 11. ([7])On Shishkin mesh, for $τ_{0} \geq 2$ the interpolation errors are bounded above and

| y_{1} (x) - {(y_{1})}^{I} (x) | \leq C \{\begin{cases} N^{- 2} {(\log N)}^{2}, & x \in Ω_{0}, \\ N^{- 2}, & x \in Ω_{s}, \end{cases} | y_{2}^{*} (x) - {(y_{2}^{*})}^{I} (x) | \leq C \{\begin{cases} N^{- 2} {(\log N)}^{2}, & x \in Ω_{0}, \\ N^{- 2}, & x \in Ω_{s} . \end{cases}

7.2 Projection error

From the error representation, the projection error⁷ at each mesh point is $P ({(y_{2}^{*})}^{I} - y_{2}^{*}) (x_{i}) = A_{h} ({(y_{2}^{*})}^{I} - y_{2}^{*}, λ^{i}) (x_{i}), x_{i} \in Ω_{ε}^{N} .$

By the definition of the bilinear form $A_{h}$ and the procedure adapted in Reference 7, one can easily prove that $| A_{h} ({(y_{2}^{*})}^{I} - y_{2}^{*}, λ^{i}) | \leq C N^{- 2} \max | ψ^{'} |^{2} .$

Similarly for the solution of the equation, the projection error is

\begin{align} P ({(y_{1})}^{I} - y_{1}) (x_{i}) & = A_{h} ({(y_{1})}^{I} - y_{1}, λ^{i}) (x_{i}), x_{i} \in Ω_{ε}^{N} \\ \leq C N^{- 2} \max | ψ^{'} |^{2} . \end{align}

7.3 Consistency error

We now estimate consistency error⁷ for Equation (10) As $K_{1} = P y_{1} - y_{1 h}$ , $K_{1} = \sum (A_{1 h} - A) (y_{1}, λ^{i}) ϕ_{i} + \sum (v (1) - v_{h} (1), λ^{i}) ϕ_{i}$ and $K_{1} (x_{i}) = 0 .$

We now estimate consistency error⁷ for Equation (11). As

K_{2} = P y_{2}^{*} - y_{2 h}^{*}

\begin{align} K_{2} & = \sum_{i = 0}^{N} (A_{h} - A) (y_{2}^{*}, λ^{i}) ϕ_{i} + \sum_{i = 0}^{N} (g^{*} - G_{h}^{*}, λ^{i}) ϕ_{i}, x_{i} \in Ω_{ε}^{N}, \\ = \sum_{i = 0}^{N} (A_{h} - A) (y_{2}^{*}, λ^{i}) ϕ_{i} + \sum_{i = 0}^{N} (g^{*} - G^{*}, λ^{i}) ϕ_{i} + \sum_{i = 0}^{N} (G^{*} - G_{h}^{*}, λ^{i}) ϕ_{i} . \end{align}

From References 7, 29, we observe that

| (g^{*} - G^{*}, λ^{i}) | \leq C N^{- 2} \ln^{2} N .

\begin{align} K_{2} (x_{i}) & = (A_{h} - A) (y_{2}^{*}, λ^{i}) + (g^{*} - G_{h}^{*}) (λ^{i}) = \int_{Ω} g^{*} λ^{i} d x - \sum_{k = 0}^{N} G_{h, k}^{*} λ^{i} \\ = \int_{Ω} g^{*} λ^{i} d x - \int_{Ω} {(g^{*})}^{I} λ^{i} d x + \int_{Ω} {(g^{*})}^{I} λ^{i} d x - \int_{Ω} {(G^{*})}^{I} λ^{i} d x + \int_{Ω} {(G^{*})}^{I} λ^{i} d x - \sum_{k = 0}^{N} G_{h, k}^{*} λ^{i} . \end{align}

Let

K_{2}^{*} (x_{i}) = \int_{Ω} {(G^{*})}^{I} λ^{i} d x - \sum_{k = 0}^{N} G_{h, k}^{*} λ^{i},

then

K_{2} (x_{i}) = \int_{Ω} g^{*} λ^{i} d x - \int_{Ω} {(g^{*})}^{I} λ^{i} d x + \int_{Ω} {(g^{*})}^{I} λ^{i} d x - \int_{Ω} {(G^{*})}^{I} λ^{i} d x + K^{*} (x_{i}) .

Now, by Simpson rule

| K_{2}^{*} (x_{i}) | = |\sum_{i = 1}^{N - 1} G_{h, k}^{*} λ^{i} d x - \int_{0}^{2} {(G^{*})}^{I} λ^{i} d x| \leq C N^{- 2} | | {(G^{*})}^{^{''}} | |_{L^{\infty} (Ω)} | | λ^{i} | |_{L^{\infty} (Ω)} \leq C N^{- 2} .

Here,

| {(G^{*})}^{^{'}} | \leq C, x \in Ω^{-}

\begin{align} |\int_{0}^{2} (g^{*} - {(g^{*})}^{I}) λ^{i} d x| \leq C (| | g^{*} - {(g^{*})}^{I} | |_{L^{\infty} (\overline{Ω})} + N^{- 2} | | g^{*} | |_{L^{1} (\overline{Ω})}) | | λ^{i} | |_{L^{1} (Ω)} \leq C N^{- 2}, \\ |\int_{0}^{2} {(g^{*})}^{I} λ^{i} d x - \int_{0}^{2} {(G^{*})}^{I} λ^{i} d x| \leq \int_{0}^{2} | {(g^{*} - G^{*})}^{I} | λ^{i} d x \leq C \int_{0}^{2} | y_{a s} - Y_{a s} | d x \leq C N^{- 2} \\ | K_{2} (x_{i}) | \leq C N^{- 2}, \\ | y_{2}^{*} (x_{i}) - y_{2 h}^{*} (x_{i}) | \leq | y_{2}^{*} - {(y_{2}^{*})}^{I} | + | P ({(y_{2}^{*})}^{I} - y_{2}^{*}) | + | P y_{2}^{*} - y_{2 h}^{*} | \leq C N^{- 2} \max | ψ^{'} |^{2} . \\ | y_{1} (x_{i}) - y_{1 h} (x_{i}) | \leq | y_{1} - y_{1}^{I} | + | P (y_{1}^{I} - y_{1}) | \leq C N^{- 2} \max | ψ^{'} |^{2} . \end{align}

Lemma 12.Let $y_{2}$ and $y_{2}^{*}$ be the solutions of (3) and (7). If $ε \leq C N^{- 1}$ , then, $| {(y_{2} - y_{2}^{*})}^{^{'}} (x) | \leq C N^{- 1}, x \in Ω$ .

Proof.Using the method of proof of [ 33, theorem 4.1] and [ 34, lemma 6.1], we have

\begin{align} - ε {(y_{2} - y_{2}^{*})}^{'} (x) + ε {(y_{2} - y_{2}^{*})}^{^{'}} (0) + \int_{0}^{x} a (t) {(y_{2} - y_{2}^{*})}^{'} d t = & - \int_{0}^{x} [b (t) (y_{2} - y_{2}^{*}) + c (t) (y_{2} - y_{2, a s})] d t, \\ \max_{Ω} ε |{(y_{2} - y_{2}^{*})}^{^{'}}| \leq C ε^{2}, \end{align}

which concludes the proof.

Theorem 1.Let $y_{1}$ be the solution of (2) and $y_{1 h}$ be its numerical solution defined by (11), then $| | | y_{1} - y_{1 h} | | | \leq C N^{- 1} \log N$ .

Proof.

\begin{align} | | | y_{1} - y_{1 h} | | |^{2} & = [ε | y_{1} - y_{1 h} |_{1}^{2} + ρ | | y_{1} - y_{1 h} | |_{0}^{2}], \\ | y_{1} - y_{1 h} |_{1}^{2} & = \int_{Ω} {|{(y_{1} - y_{1 h})}^{^{'}}|}^{2} d x \leq C N^{- 2} \log^{2} N \int_{0}^{2} |y_{1}^{^{''}}| d x \\ \leq C N^{- 2} \log^{2} N [\sum_{i = 1}^{N} \int_{x_{i - 1}}^{x_{i}} |v_{1}^{^{''}}| d x + \sum_{i = 1}^{N / 2} \int_{x_{i - 1}}^{x_{i}} |w_{1, 1}^{^{''}}| d x + \sum_{i = N / 2 + 1}^{N} \int_{x_{i - 1}}^{x_{i}} |w_{1, 2}^{^{''}}| d x] \\ \leq C N^{- 2} \log^{2} N [C + \sum_{i = 1}^{N / 4} \int_{x_{i - 1}}^{x_{i}} |w_{1, 1}^{^{''}}| d x + \sum_{i = N / 4 + 1}^{N / 2} \int_{x_{i - 1}}^{x_{i}} |w_{1, 1}^{^{''}}| d x + \sum_{i = N / 2 + 1}^{3 N / 4} \int_{x_{i - 1}}^{x_{i}} |w_{1, 2}^{^{''}}| d x + \sum_{i = 3 N / 4 + 1}^{N} \int_{x_{i - 1}}^{x_{i}} |w_{1, 2}^{^{''}}| d x] \\ \leq C N^{- 2} \log^{2} N [C + \sum_{i = 1}^{N / 4} \int_{x_{i - 1}}^{x_{i}} ε^{- 2} e^{\frac{- α (1 - x)}{ε}} d x + \sum_{N / 4 + 1}^{N / 2} \int_{x_{i - 1}}^{x_{i}} ε^{- 2} e^{\frac{- α (1 - x)}{ε}} d x \\ + \sum_{N / 2 + 1}^{3 N / 4} \int_{x_{i - 1}}^{x_{i}} ε^{- 2} e^{\frac{- α (2 - x)}{ε}} d x + \sum_{3 N / 4 + 1}^{N} \int_{x_{i - 1}}^{x_{i}} ε^{- 2} e^{\frac{- α (2 - x)}{ε}} d x] \\ \leq C ε^{- 1} N^{- 2} \log^{2} N, \\ ε | y_{1} - y_{1 h} |_{1}^{2} & \leq C N^{- 2} \log^{2} N, \\ | | | y_{1} - y_{1 h} | | | & \leq C N^{- 1} \log N . \end{align}

Theorem 2.Let $y_{2}$ and $y_{2}^{*}$ be the solutions of (3) and (7). Then, $| | | (y_{2} - y_{2}^{*}) | | | \leq C N^{- 2}$ .

Proof.Let $I_{i} = [x_{i - 1}, x_{i}]$ . Then by Lemma 12, we have

\begin{align} | | (y_{2} - y_{2}^{*}) | |_{L^{2} (I_{i})}^{2} = \int_{I_{i}} {|y_{2} - y_{2}^{*}|}^{2} d x \leq C ε^{4} h_{i} \leq C N^{- 5}, \\ | | | (y_{2} - y_{2}^{*}) | | |_{I_{i}}^{2} = [ε {|y_{2} - y_{2}^{*}|}_{1}^{2} + ρ | | (y_{2} - y_{2}^{*}) | |_{L^{2} (I_{i})}^{2}] \leq C N^{- 5}, \\ | | | (y_{2} - y_{2}^{*}) | | |^{2} = \sum_{i} | | | (y_{2} - y_{2}^{*}) | | |_{I_{i}}^{2} \leq C N^{- 4} . \end{align}

Theorem 3.Let $y_{2}^{*^{I}}$ be the interpolation of $y_{2}^{*}$ and $y_{2 h}^{*}$ be the numerical solution of $y_{2}^{*}$ . Then $| | | y_{2}^{*^{I}} - y_{2 h}^{*} | | | \leq C N^{- 2} {(\log N)}^{2}$

Proof.Let us begin with the coercivity property of the bilinear form:

\frac{1}{2} | | | (y_{2}^{*^{I}} - y_{2 h}^{*} | | |^{2} \leq A ((y_{2}^{*^{I}} - y_{2 h}^{*}), (y_{2}^{*^{I}} - y_{2 h}^{*})) .

Now using Galerkin orthogonality,³⁵ we have

\begin{align} \frac{1}{2} | | | (y_{2}^{*^{I}} - y_{2 h}^{*} | | |^{2} & \leq A ((y_{2}^{*^{I}} - y_{2 h}^{*}), (y_{2}^{*^{I}} - y_{2 h}^{*})) \\ = A_{Gal} ((y_{2}^{*^{I}} - y_{2 h}^{*}), (y_{2}^{*^{I}} - y_{2 h}^{*})) + A_{Stab} ((y_{2}^{*^{I}} - y_{2 h}^{*}), (y_{2}^{*^{I}} - y_{2 h}^{*})) \\ = A_{Gal} (η, θ) + A_{Stab} (η, θ), \end{align}

where

η = y_{2}^{*^{I}} - y_{2 h}^{*} = θ .

From the definition of the bilinear form, we have

A_{Gal} (η, θ) = ε \int_{Ω} η^{'} θ^{'} d x + \int_{Ω} a η^{'} θ d x + \int_{Ω} b η θ d x, ε \int_{Ω} η^{'} θ^{'} d x = 0 .

We apply Holder inequality to estimate the second term

| \int_{Ω} a η^{'} θ d x | = | \sum_{i = 1}^{N} \int_{x_{i - 1}}^{x_{i}} a η^{'} θ d x | = | - \sum_{i = 1}^{N} \int_{x_{i - 1}}^{x_{i}} η {(a θ)}^{'} d x | \leq C | | η | |_{L^{2} (Ω)} | | {(θ)}^{'} | |_{L^{2} (Ω)} \leq C {(N^{- 1} \log N)}^{2} | | | θ | | | .

Now for the third term

\begin{align} | \int_{Ω} b η θ d x | \leq C | | b (x) | |_{L^{2} (Ω)} | | η | |_{L^{2} (Ω)} | | θ | |_{L^{2} (Ω)} \leq C {(N^{- 1} \log N)}^{2} | | | θ | | |, \\ A_{Gal} (η, θ) \leq C {(N^{- 1} \log N)}^{2} | | | θ | | | . \end{align}

Now, A_{Stab} (η, θ) = \sum δ_{i} (- ε \int_{x_{i - 1}}^{x_{i}} η^{″} + \int_{x_{i - 1}}^{x_{i}} a η^{'} + \int_{x_{i - 1}}^{x_{i}} b η) a θ^{^{'}} d x, \leq C δ_{i} (ε \int_{Ω} η^{″} a θ^{^{'}} d x + \int_{Ω} a^{2} η^{'} θ^{^{'}} + \int_{Ω} a b η θ^{^{'}}) .

Now, using the decomposition for the solution

y^{*}

, we can evaluate the first term of the above expression. Let

I_{i} \subset Ω_{0}

, then

\begin{align} δ_{i} ε \int_{I_{i}} v^{''} a θ^{'} d x & \leq C δ_{i} ε | | a | |_{L^{2} (Ω)} (\int_{I_{i}} {(v^{''})}^{2} d x)^{1 / 2} (\int_{I_{i}} (θ^{'})^{2})^{1 / 2} \leq C δ_{i} ε (\int_{I_{i}} d x)^{1 / 2} | | | θ | | | \\ \leq C δ_{i} ε (\sum_{i = 1}^{N} \int_{x_{i - 1}}^{x_{i} d x} d x)^{1 / 2} | | | θ | | | \leq C δ_{i} ε (\sum_{i = 1}^{N} h_{i})^{1 / 2} | | | θ | | | \leq C N^{- 2} | | | θ | | | . \end{align}

The second term can be evaluated in the following manner

\begin{align} δ_{i} ε \int_{I_{i}} w_{1}^{''} a θ^{'} d x & \leq C δ_{i} ε | | a | |_{L^{2} (Ω)} (\int_{I_{i}} {(w_{1}^{''})}^{2} d x)^{1 / 2} (\int_{I_{i}} {(θ^{'})}^{2} d x)^{1 / 2} \\ \leq δ_{i} ε (\sum_{i} \int_{x_{i - 1}}^{x_{i}} ε^{- 2} e^{\frac{- 2 α (2 - x)}{ε}}) d x)^{1 / 2} | | | θ | | | \\ \leq δ_{i} ε (\sum_{i} ε^{- 1} e^{\frac{- 2 α (2 - x_{i})}{ε}})^{1 / 2} | | | θ | | | \leq C δ_{i} ε^{1 / 2} (\sum N^{- 2})^{1 / 2} | | | θ | | | \leq C N^{- 2} | | | θ | | | . \end{align}

In a similar manner, we can prove the following $δ_{i} ε \int_{I_{i}} w_{2}^{''} a θ^{'} d x \leq C N^{- 2} | | | θ | | |,$ $I_{i} \subset Ω_{0},$

\begin{align} δ_{i} \int_{I_{i}} a^{2} η^{^{'}} θ^{^{'}} d x & \leq C δ_{i} \int_{I_{i}} a^{2} v^{^{'}} θ^{^{'}} d x \leq C δ_{i} | | a^{2} (x) | |_{L^{2} (Ω)} (\int_{I_{i}} {(v^{^{'}})}^{2} d x)^{1 / 2} (\int_{I_{i}} {(θ^{^{'}})}^{2} d x)^{1 / 2} \\ \leq C δ_{i} | | a^{2} (x) | |_{L^{2} (Ω)} (\int_{I_{i}} ε^{2} d x)^{1 / 2} | | | θ | | | \\ \leq C δ_{i} ε (\sum_{i} h_{i})^{1 / 2} | | | θ | | | \leq C δ_{i} ε (\sum_{i} ε N^{- 1} \log N)^{1 / 2} | | | θ | | | \\ \leq C N^{- 2} {(\log N)}^{1 / 2} | | | θ | | | \leq C N^{- 2} {(\log N)}^{2} | | | θ | | | . \end{align}

Also, we can prove the following result $δ_{i} \int_{Ω_{0}} a b η^{'} θ^{'} d x \leq C N^{- 2} {(\log N)}^{2} | | | θ | |$ . Therefore,

\begin{align} | | | y_{2}^{*^{I}} - y_{2 h}^{*} | | |^{2} \leq C N^{- 2} {(\log N)}^{2} | | | (y_{2}^{*^{I}} - y_{2 h}^{*} | | |, \\ | | | y_{2}^{*^{I}} - y_{2 h}^{*} | | | \leq C N^{- 2} {(\log N)}^{2}, \end{align}

which concludes the proof.

Theorem 4.Let $y_{2}^{*}$ be the solution of (3) and ${(y_{2}^{*})}^{I}$ be its interpolant. Then we have $| | | y_{2}^{*} - {(y_{2}^{*})}^{I} | | | \leq C N^{- 1} \log^{3 / 2} N .$

Proof.Let $I_{i} = [x_{i - 1}, x_{i}]$ , then

\begin{align} | | y_{2}^{*} - y_{2}^{*^{I}} | |_{0}^{2} & = \sum_{I_{i}} \int_{I_{i}} {|y_{2}^{*} - y_{2}^{*^{I}}|}^{2} d x \leq C N^{- 4} \log^{4} N \sum \int_{I_{i}} d x \leq C N^{- 4} \log^{4} N . \\ | | {(y_{2}^{*} - y_{2}^{*^{I}})}^{^{'}} | |_{0}^{2} & = \int_{0}^{2} {|{(y_{2}^{*} - y_{2}^{*^{I}})}^{^{'}} (x)|}^{2} d x, \end{align}

and integration by parts, Lemma 12, we have

\begin{align} {||{(y_{2}^{*} - y_{2}^{*^{I}})}^{^{'}}||}^{2} & \leq C N^{- 2} \log^{2} N [\sum_{I_{i} \subset Ω^{-} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} (|v^{″}| + |w_{2, 1}^{''}| + |w_{2, 2}^{''}|) d x + \sum_{I_{i} \subset Ω^{-} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} (|v^{″}| + |w_{2, 1}^{''}| + |w_{2, 2}^{''}|) d x \\ + \sum_{I_{i} \subset Ω^{+} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} (|v^{″}| + |w_{2, 1}^{''}| + |w_{2, 2}^{''}|) d x + \sum_{I_{i} \subset Ω^{+} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} (|v^{″}| + |w_{2, 1}^{''}| + |w_{2, 2}^{''}|) d x] . \end{align}

For the regular part, $\sum_{I_{i}} \int_{I_{i}} | v^{''} | d x \leq C .$ For the singular part,

\begin{align} \sum_{I_{i}} \int_{I_{i}} | w_{2, 1}^{''} | d x & = \sum_{I_{i} \subset Ω^{-} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 1}^{''} | d x + \sum_{I_{i} \subset Ω^{-} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 1}^{''} | d x + \sum_{I_{i} \subset Ω^{+} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 1}^{''} | d x + \sum_{I_{i} \subset Ω^{+} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 1}^{''} | d x \\ \leq C [ε^{- 2} \sum_{i = 1}^{N / 4} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (2 - x)}{ε}} d x + ε^{- 2} \sum_{i = N / 4 + 1}^{N / 2} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (2 - x)}{ε}} d x \\ + ε^{- 2} \sum_{i = N / 2 + 1}^{3 N / 4} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (2 - x)}{ε}} d x + ε^{- 2} \sum_{i = 3 N / 4 + 1}^{N} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (2 - x)}{ε}} d x] \\ \leq C ε^{- 1} . \end{align}

\begin{align} \sum_{I_{i}} \int_{I_{i}} | w_{2, 2}^{''} | d x & = \sum_{I_{i} \subset Ω^{-} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 2}^{''} | d x + \sum_{I_{i} \subset Ω^{-} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 2}^{''} | d x + \sum_{I_{i} \subset Ω^{+} \cap Ω_{s}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 2}^{''} | d x + \sum_{I_{i} \subset Ω^{+} \cap Ω_{0}} \int_{x_{i - 1}}^{x_{i}} | w_{2, 2}^{''} | d x \\ \leq C [ε^{- 1} \sum_{i = 1}^{i = N / 4} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (1 - x)}{ε}} d x + ε^{- 1} \sum_{i = N / 4 + 1}^{N / 2} \int_{x_{i - 1}}^{x_{i}} e^{\frac{- α (1 - x)}{ε}} d x + ε^{- 1} \sum_{i = N / 2 + 1}^{3 N / 4} \int_{x_{i - 1}}^{x_{i}} d x + ε^{- 1} \sum_{i = 3 N / 4 + 1}^{N} \int_{x_{i - 1}}^{x_{i}} d x] \leq C ε^{- 1} . \end{align}

Combining all the above estimates, we have

\begin{align} {||{(y_{2}^{*} - y_{2}^{*^{I}})}^{^{'}}||}_{0}^{2} & \leq C ε^{- 1} N^{- 2} \log^{2} N and ε {||{(y_{2}^{*} - y_{2}^{*^{I}})}^{^{'}}||}_{0}^{2} \leq C N^{- 2} \log^{2} N, \\ {|||y_{2}^{*} - y_{2}^{*^{I}}|||}^{2} & = [ε {|y_{2}^{*} - y_{2}^{*^{I}}|}_{1}^{2} + ρ {||y_{2}^{*} - y_{2}^{*^{I}}||}_{0}^{2}] \leq [C N^{- 2} \log^{2} N + ρ C N^{- 4} \log^{4} N] \leq C N^{- 2} \log^{2} N, \end{align}

which concludes the proof.

Theorem 5.Let y and $y_{h} = y_{1 h} + y_{2 h}^{*}$ be the exact and numerical solutions of (1), respectively. Then $| | | y - y_{h} | | | \leq C N^{- 1} \log N .$

Proof.By triangle inequality and by Theorems 1,2,3 and 4, we have

\begin{align} | | | y - y_{h} | | | & = | | | y_{1} + y_{2} - y_{1 h} - y_{2 h}^{*} | | | \leq | | | y_{1} - y_{1 h} | | | + | | | y_{2} - y_{2 h}^{*} | | | \\ \leq | | | y_{1} - y_{1 h} | | | + | | | y_{2} - y_{2}^{*} | | | + | | | y_{2}^{*} - y_{2}^{*^{I}} | | | + | | | y_{2}^{*^{I}} - y_{2 h}^{*} | | | \leq C N^{- 1} \log N, \end{align}

which concludes the proof.

8 NUMERICAL EXAMPLE PROBLEMS

We measure the accuracy of the result in

C^{0}

-norm,

L^{2}

-norm, and

H^{1}

-norm. The computational rate of convergence is computed using the following formula

p^{M} = \log_{2} [\frac{D^{M} + M^{- 2}}{D^{2 M} + M^{- 2}}], D^{M} = \{\begin{cases} | | y_{i}^{*^{M}} - y_{2 i}^{*^{2 M}} | |_{\infty}, & for C^{0} -norm, \\ | | y_{i}^{*^{M}} - y_{2 i}^{*^{2 M}} | |_{L^{2} (Ω)}, & for L^{2} -norm, \\ | | | y_{i}^{*^{M}} - y_{2 i}^{*^{2 M}} | | |_{H^{1} (Ω)}, & for H^{1} -norm, \end{cases}

where

y_{i}^{*^{M}}

and

y_{2 i}^{*^{2 M}}

are the ith components of the numerical solutions on meshes of M and

2 M

points, respectively.

Note: Usually the experimental rate of convergence is $p^{M} = \log_{2} [\frac{D^{M}}{D^{2 M}}] .$ The asymptotic expansion approximation is used to convert delay differential equation into a differential equation. An upper bound of absolute difference of y and $y^{*}$ is $O (ε^{2}) .$ In order to incorporate the absolute difference of y and $y^{*}$ in the computation of $p^{M},$ the maximum value of $ε^{2},$ that is $M^{- 2}$ is added with $D^{M}$ and $D^{2 M} .$

Example 1.Consider the problem (1) with the following data functions

a (x) = 5 + x; b (x) = 1; c (x) = - 1 / 2; f (x) = 1 + x^{2} .

Figure 1 represents the numerical solutions of

y, y_{1}

, and

y_{2}^{*} .

Tables 1, 2, and 3, respectively present the maximum pointwise error in

C^{0}

-norm,

L^{2}

-norm, and

H^{1}

-norm.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Numerical solution of the Example 1

TABLE 1. Numerical results of the Example 1 using maximum norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	1.2252e $-$ 2	2.3555e $-$ 3	4.4274e $-$ 4	1.9316e $-$ 4	1.5981e $-$ 5	3.2432e $-$ 6	7.6756e $-$ 7
$2^{- 7}$	1.2279e $-$ 2	2.3647e $-$ 3	4.4626e $-$ 4	9.8586e $-$ 5	4.8643e $-$ 5	4.2965e $-$ 6	8.7350e $-$ 7
$2^{- 8}$	1.2290e $-$ 2	2.3694e $-$ 3	4.4806e $-$ 4	9.9047e $-$ 5	2.2702e $-$ 5	1.2261e $-$ 5	1.1170e $-$ 6
$2^{- 9}$	1.2290e $-$ 2	2.3718e $-$ 3	4.4898e $-$ 4	9.9280e $-$ 5	2.2775e $-$ 5	5.4222e $-$ 6	3.0856e $-$ 6
$2^{- 10}$	1.2281e $-$ 2	2.3732e $-$ 3	4.4950e $-$ 4	9.9401e $-$ 5	2.2812e $-$ 5	6.1711e $-$ 6	1.3317e $-$ 6
$2^{- 11}$	1.2258e $-$ 2	2.3742e $-$ 3	4.4987e $-$ 4	9.9468e $-$ 5	2.2831e $-$ 5	5.4383e $-$ 6	1.3332e $-$ 6
$2^{- 12}$	1.2208e $-$ 2	2.3754e $-$ 3	4.5027e $-$ 4	9.9516e $-$ 5	2.2842e $-$ 5	5.4411e $-$ 6	1.3339e $-$ 6
$2^{- 13}$	1.2109e $-$ 2	2.3773e $-$ 3	4.5091e $-$ 4	9.9568e $-$ 5	2.2849e $-$ 5	5.4426e $-$ 6	1.3343e $-$ 6
$2^{- 14}$	1.1912e $-$ 2	2.3808e $-$ 3	4.5209e $-$ 4	9.9651e $-$ 5	2.2856e $-$ 5	5.4435e $-$ 6	1.3345e $-$ 6
$2^{- 15}$	1.3240e $-$ 2	2.3877e $-$ 3	4.5442e $-$ 4	9.9805e $-$ 5	2.2867e $-$ 5	5.4444e $-$ 6	1.3346e $-$ 6
$D^{N}$	1.3240e $-$ 2	2.3877e $-$ 3	4.5442e $-$ 4	9.9805e $-$ 5	2.2867e $-$ 5	5.4444e $-$ 6	1.3346e $-$ 6
$p^{N}$	2.4611	2.3823	2.1804	2.1210	2.0676	2.0272	-

TABLE 2. Numerical results of the Example 1 using

L^{2}

norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	1.8693e $-$ 3	3.7172e $-$ 4	7.8911e $-$ 5	4.8203e $-$ 5	3.6366e $-$ 6	8.9134e $-$ 7	2.2471e $-$ 7
$2^{- 7}$	1.7521e $-$ 3	3.3645e $-$ 4	6.8015e $-$ 5	1.4722e $-$ 5	9.5756e $-$ 6	7.7801e $-$ 7	1.9206e $-$ 7
$2^{- 8}$	1.6909e $-$ 3	3.1669e $-$ 4	6.1585e $-$ 5	1.2688e $-$ 5	2.8036e $-$ 6	1.9274e $-$ 6	1.6855e $-$ 7
$2^{- 9}$	1.6649e $-$ 3	3.0607e $-$ 4	5.8007e $-$ 5	1.1506e $-$ 5	2.4314e $-$ 6	5.4899e $-$ 7	3.9994e $-$ 7
$2^{- 10}$	1.6730e $-$ 3	3.0051e $-$ 4	5.6073e $-$ 5	1.0854e $-$ 5	2.2183e $-$ 6	4.8354e $-$ 7	1.1182e $-$ 7
$2^{- 11}$	1.7569e $-$ 3	2.9816e $-$ 4	5.5004e $-$ 5	1.0503e $-$ 5	2.1021e $-$ 6	4.4683e $-$ 7	1.0089e $-$ 7
$2^{- 12}$	2.0759e $-$ 3	3.0030e $-$ 4	5.4347e $-$ 5	1.0310e $-$ 5	2.0403e $-$ 6	4.2711e $-$ 7	9.4906e $-$ 8
$2^{- 13}$	3.0325e $-$ 3	3.1695e $-$ 4	5.3900e $-$ 5	1.0187e $-$ 5	2.0069e $-$ 6	4.1675e $-$ 7	9.1749e $-$ 8
$2^{- 14}$	5.3547e $-$ 3	3.8412e $-$ 4	5.3901e $-$ 5	1.0081e $-$ 5	1.9865e $-$ 6	4.1126e $-$ 7	9.0113e $-$ 8
$2^{- 15}$	1.0319e $-$ 2	5.8798e $-$ 4	5.6131e $-$ 5	9.9562e $-$ 6	1.9695e $-$ 6	4.0808e $-$ 7	8.9261e $-$ 8
$D^{N}$	1.0319e $-$ 2	5.8798e $-$ 4	6.1585e $-$ 5	1.1506e $-$ 5	2.2183e $-$ 6	4.4683e $-$ 7	9.4906e $-$ 8
$p^{N}$	4.0246	3.0782	2.3265	2.2720	2.2107	2.1489	-

TABLE 3. Numerical results of the Example 1 using

H^{1}

norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	8.5205e $-$ 2	3.7253e $-$ 2	1.6575e $-$ 2	1.4329e $-$ 2	4.0263e $-$ 3	2.0287e $-$ 3	9.6511e $-$ 4
$2^{- 7}$	8.5287e $-$ 2	3.7270e $-$ 2	1.6511e $-$ 2	8.0595e $-$ 3	7.2341e $-$ 3	2.1597e $-$ 3	1.0100e $-$ 3
$2^{- 8}$	8.5309e $-$ 2	3.7285e $-$ 2	1.6498e $-$ 2	8.0109e $-$ 3	3.7632e $-$ 3	3.7186e $-$ 3	1.0615e $-$ 3
$2^{- 9}$	8.5278e $-$ 2	3.7293e $-$ 2	1.6495e $-$ 2	7.9959e $-$ 3	3.7322e $-$ 3	1.9562e $-$ 3	1.8572e $-$ 3
$2^{- 10}$	8.5184e $-$ 2	3.7295e $-$ 2	1.6495e $-$ 2	7.9905e $-$ 3	3.7216e $-$ 3	1.9398e $-$ 3	9.3555e $-$ 4
$2^{- 11}$	8.5006e $-$ 2	3.7291e $-$ 2	1.6496e $-$ 2	7.9884e $-$ 3	3.7174e $-$ 3	1.9340e $-$ 3	9.2659e $-$ 4
$2^{- 12}$	8.4761e $-$ 2	3.7282e $-$ 2	1.6500e $-$ 2	7.9880e $-$ 3	3.7156e $-$ 3	1.9316e $-$ 3	9.2334e $-$ 4
$2^{- 13}$	8.4757e $-$ 2	3.7273e $-$ 2	1.6506e $-$ 2	7.9887e $-$ 3	3.7149e $-$ 3	1.9306e $-$ 3	9.2198e $-$ 4
$2^{- 14}$	8.6678e $-$ 2	3.7291e $-$ 2	1.6520e $-$ 2	7.9911e $-$ 3	3.7148e $-$ 3	1.9301e $-$ 3	9.2135e $-$ 4
$2^{- 15}$	9.7436e $-$ 2	3.7481e $-$ 2	1.6550e $-$ 2	7.9963e $-$ 3	3.7153e $-$ 3	1.9299e $-$ 3	9.2106e $-$ 4
$D^{N}$	9.7436e $-$ 2	3.7481e $-$ 2	1.6550e $-$ 2	7.9963e $-$ 3	3.7216e $-$ 3	1.9340e $-$ 3	9.2334e $-$ 4
$p^{N}$	1.3796	1.1803	1.0501	1.1037	9.4451e $-$ 1	1.0668	–

Example 2.Consider the problem (1) with the following data functions

a (x) = 5 + x^{2} / 4; b (x) = 2; c (x) = - 1 / 2; f (x) = \exp (- 1 / x) .

Figure 2 represents the numerical solutions of

y, y_{1}

, and

y_{2}^{*} .

Tables 4, 5, and 6, respectively present the maximum pointwise error in

C^{0}

-norm,

L^{2}

-norm, and

H^{1}

-norm.

TABLE 4. Numerical results of the Example 2 using maximum norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	2.7317e $-$ 3	5.3720e $-$ 4	1.0338e $-$ 4	3.3405e $-$ 5	4.4124e $-$ 6	1.0882e $-$ 6	2.7551e $-$ 7
$2^{- 7}$	2.7446e $-$ 3	5.3906e $-$ 4	1.0374e $-$ 4	2.3629e $-$ 5	8.2131e $-$ 6	1.1170e $-$ 6	2.8341e $-$ 7
$2^{- 8}$	2.7641e $-$ 3	5.4089e $-$ 4	1.0397e $-$ 4	2.3690e $-$ 5	5.5286e $-$ 6	2.0605e $-$ 6	2.8741e $-$ 7
$2^{- 9}$	2.7998e $-$ 3	5.4359e $-$ 4	1.0418e $-$ 4	2.3727e $-$ 5	5.5369e $-$ 6	1.3566e $-$ 6	5.2222e $-$ 7
$2^{- 10}$	2.8696e $-$ 3	5.4851e $-$ 4	1.0448e $-$ 4	2.3760e $-$ 5	5.5418e $-$ 6	1.3577e $-$ 6	3.4386e $-$ 7
$2^{- 11}$	3.0078e $-$ 3	5.5812e $-$ 4	1.0501e $-$ 4	2.3805e $-$ 5	5.5458e $-$ 6	1.3584e $-$ 6	3.4402e $-$ 7
$2^{- 12}$	3.4555e $-$ 3	5.7720e $-$ 4	1.0604e $-$ 4	2.3883e $-$ 5	5.5509e $-$ 6	1.3589e $-$ 6	3.4411e $-$ 7
$2^{- 13}$	6.4710e $-$ 3	6.1523e $-$ 4	1.0809e $-$ 4	2.4036e $-$ 5	5.5595e $-$ 6	1.3595e $-$ 6	3.4417e $-$ 7
$2^{- 14}$	1.2512e $-$ 2	8.0016e $-$ 4	1.1392e $-$ 4	2.4337e $-$ 5	5.5761e $-$ 6	1.3605e $-$ 6	3.4424e $-$ 7
$2^{- 15}$	2.4634e $-$ 2	1.4859e $-$ 3	1.2618e $-$ 4	2.4939e $-$ 5	5.6089e $-$ 6	1.3623e $-$ 6	3.4436e $-$ 7
$D^{N}$	2.4634e $-$ 2	1.4859e $-$ 3	1.2618e $-$ 4	2.4939e $-$ 5	5.6089e $-$ 6	1.3623e $-$ 6	3.4436e $-$ 7
$p^{N}$	4.0074	3.4512	2.2983	2.1314	2.0355	1.9865	–

TABLE 5. Numerical results of the Example 2 using

L^{2}

norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	4.8034e $-$ 4	1.0703e $-$ 4	2.5571e $-$ 5	1.6743e $-$ 5	1.1929e $-$ 6	2.9352e $-$ 7	7.2566e $-$ 8
$2^{- 7}$	4.9829e $-$ 4	1.0544e $-$ 4	2.4897e $-$ 5	6.1054e $-$ 6	4.1892e $-$ 6	3.0709e $-$ 7	7.6296e $-$ 8
$2^{- 8}$	5.6623e $-$ 4	1.0791e $-$ 4	2.4719e $-$ 5	6.0210e $-$ 6	1.4934e $-$ 6	1.0474e $-$ 6	7.8207e $-$ 8
$2^{- 9}$	7.2015e $-$ 4	1.1588e $-$ 4	2.4983e $-$ 5	5.9958e $-$ 6	1.4820e $-$ 6	3.6926e $-$ 7	2.6183e $-$ 7
$2^{- 10}$	1.0392e $-$ 3	1.3342e $-$ 4	2.5831e $-$ 5	6.0200e $-$ 6	1.4781e $-$ 6	3.6768e $-$ 7	9.1787e $-$ 8
$2^{- 11}$	1.6850e $-$ 3	1.6952e $-$ 4	2.7694e $-$ 5	6.1064e $-$ 6	1.4799e $-$ 6	3.6707e $-$ 7	9.1565e $-$ 8
$2^{- 12}$	2.9823e $-$ 3	2.4254e $-$ 4	3.1513e $-$ 5	6.2984e $-$ 6	1.4884e $-$ 6	3.6715e $-$ 7	9.1473e $-$ 8
$2^{- 13}$	5.5816e $-$ 3	3.8936e $-$ 4	3.9224e $-$ 5	6.6927e $-$ 6	1.5079e $-$ 6	3.6797e $-$ 7	9.1467e $-$ 8
$2^{- 14}$	1.0787e $-$ 2	6.8367e $-$ 4	5.4728e $-$ 5	7.4877e $-$ 6	1.5482e $-$ 6	3.6994e $-$ 7	9.1543e $-$ 8
$2^{- 15}$	2.1218e $-$ 2	1.2728e $-$ 3	8.5838e $-$ 5	9.0846e $-$ 6	1.6295e $-$ 6	3.7403e $-$ 7	9.1739e $-$ 8
$D^{N}$	2.1218e $-$ 2	1.2728e $-$ 3	8.5838e $-$ 5	9.0846e $-$ 6	1.6295e $-$ 6	3.7403e $-$ 7	9.1739e $-$ 8
$p^{N}$	4.0081	3.7218	2.9704	2.3201	2.0765	2.0168	–

TABLE 6. Numerical results of the Example 2 using

H^{1}

norm

$ε ↓$	64	128	256	512	1024	2048	4096
	N (Number of mesh points)
$2^{- 6}$	2.4495e $-$ 2	1.0832e $-$ 2	4.7925e $-$ 3	2.7468e $-$ 3	9.8499e $-$ 4	5.1484e $-$ 4	2.4819e $-$ 4
$2^{- 7}$	2.4558e $-$ 2	1.0847e $-$ 2	4.7961e $-$ 3	2.3243e $-$ 3	1.3343e $-$ 3	5.1723e $-$ 4	2.4874e $-$ 4
$2^{- 8}$	2.4657e $-$ 2	1.0862e $-$ 2	4.7996e $-$ 3	2.3241e $-$ 3	1.0905e $-$ 3	6.9467e $-$ 4	2.4979e $-$ 4
$2^{- 9}$	2.4859e $-$ 2	1.0887e $-$ 2	4.8036e $-$ 3	2.3246e $-$ 3	1.0898e $-$ 3	5.7000e $-$ 4	3.4530e $-$ 4
$2^{- 10}$	2.5337e $-$ 2	1.0935e $-$ 2	4.8101e $-$ 3	2.3255e $-$ 3	1.0897e $-$ 3	5.6955e $-$ 4	2.7884e $-$ 4
$2^{- 11}$	2.6583e $-$ 2	1.1040e $-$ 2	4.8223e $-$ 3	2.3269e $-$ 3	1.0899e $-$ 3	5.6941e $-$ 4	2.7857e $-$ 4
$2^{- 12}$	3.0071e $-$ 2	1.1285e $-$ 2	4.8474e $-$ 3	2.3298e $-$ 3	1.0902e $-$ 3	5.6939e $-$ 4	2.7847e $-$ 4
$2^{- 13}$	3.9655e $-$ 2	1.1914e $-$ 2	4.9013e $-$ 3	2.3354e $-$ 3	1.0908e $-$ 3	5.6943e $-$ 4	2.7844e $-$ 4
$2^{- 14}$	6.3288e $-$ 2	1.3625e $-$ 2	5.0243e $-$ 3	2.3472e $-$ 3	1.0922e $-$ 3	5.6956e $-$ 4	2.7844e $-$ 4
$2^{- 15}$	1.1529e $-$ 1	1.8199e $-$ 2	5.3264e $-$ 3	2.3720e $-$ 3	1.0949e $-$ 3	5.6984e $-$ 4	2.7846e $-$ 4
$D^{N}$	1.1529e $-$ 1	1.8199e $-$ 2	5.3264e $-$ 3	2.3720e $-$ 3	1.0949e $-$ 3	5.6984e $-$ 4	2.7847e $-$ 4
$p^{N}$	2.6616	1.7733	1.1689	1.1163	9.4285e $-$ 1	1.0333	–

9 DISCUSSION

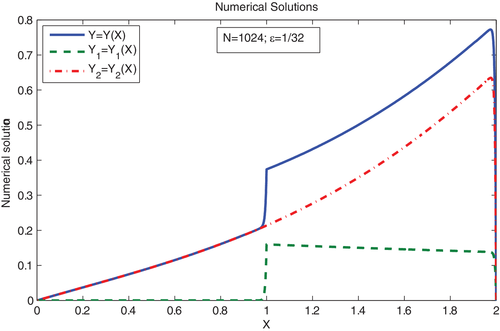
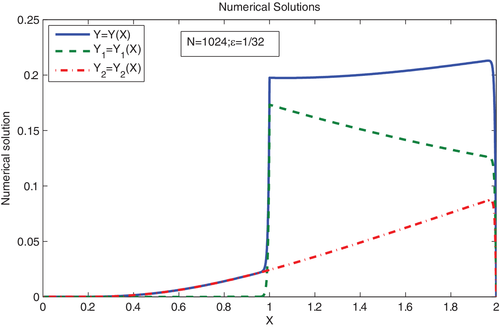
Singularly perturbed boundary value problems for delay differential equations with point source term are considered in this article. The solution of the problems is divided into two functions. One is the solution of singularly perturbed nondelay differential equation with point source and the other one is the solution of the delay differential equation with continuous source term. The error estimates in $L^{2}$ -norm for nondelay problem are available in the literature. The convergence of the error in $H^{1}$ -norm is established in this article. For the delay problem with continuous source term, first, an asymptotic expansion approximation is applied to convert the delay differential equation into nondelay differential equations. Then after converting the equation, an SDFEM is applied to singularly perturbed convection-diffusion type differential equations on Shishkin mesh. Also, the SDFEM is applied for a nondelay differential equation with point source term. It is proved that both numerical solutions converge, hence the numerical solution of the original solution converges. Furthermore, it is proved that the order of accuracy of the present method is almost two in $C^{0}$ -norm and $L^{2}$ -norm, whereas first-order convergence in $H^{1}$ -norm. Tables 1 to 6 present the maximum error using the $C^{0}$ , $L^{2}$ and $H^{1}$ norms. In Tables 1 to 6, the $p^{M'}$ s are calculated using $\log_{2} [\frac{D^{M} + M^{- 2}}{D^{2 M} + M^{- 2}}]$ . Since the absolute difference of y and $y^{*}$ is not incorporated in $D^{M},$ then $M^{- 2}$ is added in appropriate places and calculated the computational rate of convergence $p^{M}$ . Further $D^{N'}$ s are calculated subject to the condition that $ε \leq C N^{- 1}$ . Figures 1 and 2 present the numerical solutions of the test problems stated in Examples 1 and 2. From the figures, we can observe that the solution of the problem (1) exhibits the interior layer at $x = 1$ and the boundary layer at $x = 2$ . Further the solution $y_{2}^{*}$ exhibits the boundary layer at $x = 2$ and less severe layer at $x = 1 .$

CONFLICT OF INTEREST

The authors declare no potential conflict of interests.

AUTHOR CONTRIBUTIONS

All authors have equally contributed to this work. All authors read and approved the final manuscript.

Biographies

Senthilkumar Sethurathinam received his M.Sc. (Mathematics) from Department of Mathematics, Jammal Mohamed College, Tiruchirappalli and M.Phil (Mathematics) from Department of Mathematics, National college, Tiruchirappalli. He has published two research articles in international journals and three in conference proceedings. He has more than 20 years of teaching and almost 4 years of research experience. Currently, he is working as an assistant professor in the Department of Mathematics, SRM Institute of Science and Technology, Kattankulathur, Chengalpattu District 603203, Tamilnadu. His current areas of interest are numerical analysis of singular perturbation problems.
Subburayan Veerasamy received his M.Sc. (Mathematics) and Ph.D. (Mathematics) from Department of Mathematics, Bharathidasan University. He has published more than 18 research articles in international journals and four in conference proceedings. He has almost 8 years of teaching and 12 years of research experience. Currently, he is working as an assistant professor (Sr. G) in the Department of Mathematics, SRM Institute of Science and Technology, Kattankulathur, Chengalpattu District 603203, Tamilnadu. His current area of interest is numerical analysis of singular perturbation problems for ordinary and partial differential equations.
Rameshbabu Arasamudi received his M.Sc. (Mathematics) and Ph.D. (Mathematics) from Department of Mathematics, Bharathidasan University. He secured 65th rank at GATE-2003 with 95.16% and also hold University Research Studentship award during 2005–2008. He has published more than 14 research articles in international journals and two in conference proceedings. He has more than 13 years of teaching and 15 years of research experience. Currently, he is working as an assistant professor (Sr. G) in the Department of Mathematics, School of Engineering, AMRITA Vishwa Vidyapeetham, Coimbatore 641112, Tamilnadu. His areas of interest are theory and numerics of singular perturbation problems, gross Pitoskii equations (dynamical system), and device modeling (VLSI).
Ravi P. Agarwal has been actively involved in research as well as pedagogical activities for the last 49 years. His major research interests include numerical analysis, differential and difference equations, inequalities, and fixed point theorems. He has published 46 research monographs and more than 1700 publications (with almost 500 mathematicians all over the world) in prestigious national and international mathematics journals. Dr. Agarwal worked previously either as a regular faculty or as a visiting professor and scientist in universities in several countries, including India, Germany, Italy, Canada, Australia, USA, Singapore, and Japan. He has held several positions including Visiting Professor, Visiting Scientist, and Professor at various universities in different parts of the world. Specially, during 1980–1981, he was awarded most respected Alexander Von Humboldt Foundation Fellowship to work with Prof. Dr. G. Hammerlin at der Ludwig - Maximilians Universitat, Munchen, Germany, and during (1981–1982) he worked as a Visiting Professor with Prof. Roberto Conti, Instituto Matematico, Firenze, Italy. He has been ranked as a Highly Cited Researcher for 14 consecutive years, and has also been recognized as one of the “World's Most Influential Scientific Minds” in 2014 and 2015 by Thomas Reuters (World's most prestigious scientific organization). In 2020 he has been listed among World's Top 2% Scientists by Stanford University. According to Google Scholar, Dr. Agarwal is cited more than 40,000 times, and on MathSciNet, his work is cited more than 16,000 times by 6200 scientists. Dr. Agarwal is the recipient of several notable honors and awards, including Doctor Honoris Causa (2015 by University of Constanta, Romania), Professor Honoris Causa (2015 by University of Cluj, Romania), Honorary Doctorate (2017 by University of Nis, Serbia), Doctor Honoris Causa (2017 by Plovdiv University, Bulgaria), Doctor Honoris Causa (2017 by Constantin Brancusi, University of Targu-Jiu, Romania), Doctor Honoris Causa (2017 by University of Oradea, Romania, 2017), Doctor Honoris Causa (by 1 December 1918, University of Alba Lulia, Romania), Honorary Doctorate (2019 by Istanbul Gelisim University, Turkey), and Doctor Honoris Causa (2019 by Transilvania University of Brasov, Romania). He was also nominated as a possible candidate for a Banco Bilbao Vizcaya Argentaria (BBVA) Foundation Frontiers of Knowledge Award, an international award scheme recognizing significant contributions in the areas of scientific research and cultural creation. Many BBVA award winners are Nobel laureates, including Stephen Hawkins. Florida Institute of Technology (USA) and King Abdulaziz University have recently offered him Distinguished University Professorship of Mathematics. Dr. Agarwal regularly disseminates his research at invited talks/colloquiums (over 100 Institutions all over the world). He has been invited to give plenary/keynote lectures at international conferences in the USA, Russia, Italy, India, Portugal, Poland, Spain, Vietnam, China, Taiwan, Korea, Malaysia, Thailand, Romania, Saudi Arabia, Germany, Canada, Singapore, Turkey, Ukraine, Greece, and Japan. He has served over 40 journals in the capacity of an editor/honorary Editor, or associate editor.

REFERENCES

1Linß T, Madden N. A finite element analysis of a coupled system of singularly perturbed reaction-diffusion equations. Appl Math Comput. 2004; 148: 869-880.
Web of Science® Google Scholar
2Zarin H. On discontinuous Galerkin finite element method for singularly perturbed delay differential equations. Appl Math Lett. 2014; 38: 27-32.
10.1016/j.aml.2014.06.013
Web of Science® Google Scholar
3Nicaise S, Xenophontons C. Robust approximation of singularly perturbed delay differential equations by hp finite element method. Comput Methods Appl Math. 2013; 13(1): 21-37.
10.1515/cmam-2012-0001
Web of Science® Google Scholar
4Senthilkumar L, Subburayan V. A SDFEM for singularly perturbed system of convection-diffusion delay differential equations. Proceedings of the IOP Conference Series: Materials Science and Engineering; Vol. 1130, 2021:1-17; IOP Publishing.
Google Scholar
5Roos H, Zarin H. A second-order scheme for singularly perturbed differential equations with discontinuous source term. J Numer Math. 2002; 10(4): 275-289.
10.1515/JNMA.2002.275
Google Scholar
6Liu LB, Leng H, Long G. Analysis of the SDFEM for singularly perturbed differential-difference equations. Calcolo. 2018; 55(3): 1-17.
10.1007/s10092-018-0265-4
Web of Science® Google Scholar
7Ramesh Babu A, Ramanujam N. The SDFEM for singularly perturbed convection diffusion problems with discontinuous source term arising in the chemical reactor theory. Int J Comput Math. 2011; 88(8): 1664-1680.
10.1080/00207160.2010.521815
Web of Science® Google Scholar
8Becher S. Analysis of Galerkin and streamline-diffusion FEMs on piecewise equidistant meshes for turning point problems exhibiting an interior layer. Appl Numer Math. 2018; 123: 121-136.
10.1016/j.apnum.2017.09.005
Web of Science® Google Scholar
9Chen L, Xu J. Stability and accuracy of adapted finite element methods for singularly perturbed problems. Numer Math. 2008; 109(2): 167-191.
10.1007/s00211-007-0118-6
Web of Science® Google Scholar
10Mahendran R, Subburayan V. Fitted finite difference method for third order singularly perturbed delay differential equations of convection diffusion type. Int J Comput Methods 2018; 15(1): 1840007, ( 1–17).
Google Scholar
11Subburayan V, Mahendran R. An $ϵ -$ uniform numerical method for third order singularly perturbed delay differential equations with discontinuous convection coefficient and source term. Appl Math Comput. 2018; 331: 404-415.
Web of Science® Google Scholar
12Subburayan V, Mahendran R. Asymptotic numerical method for third-order singularly perturbed convection diffusion delay differential equations. Comput Appl Math. 2020; 39(3): 1-21.
10.1007/s40314-020-01223-6
Web of Science® Google Scholar
13Subburayan V, Ramanujam N. An asymptotic numerical method for singularly perturbed convection-diffusion problems with a negative shift. Neural Parallel Sci Comput. 2013; 21: 431-446.
Google Scholar
14Subburayan V, Ramanujam N. An initial value technique for singularly perturbed convection-diffusion problems with a delay. J Optim Theory Appl. 2013; 158(1): 234-250.
10.1007/s10957-012-0200-9
Web of Science® Google Scholar
15Linß T, , Madden N. An improved error estimate for a numerical method for a system of coupled singularly perturbed reaction diffusion equations. Comput Methods Appl Math 2003; 3(3): 417–423.
10.2478/cmam-2003-0027
Google Scholar
16 Shivhare M, Pramod Chakravarthy P, Ramos H, Vigo-Aguiar J. Quadratic B-spline collocation method for time dependent singularly perturbed differential-difference equation arising in the modeling of neuronal activity. Numer Methods Part Differ Equ. 2021. doi:10.1002/num.22738
10.1002/num.22738
Web of Science® Google Scholar
17Chandru M, Das P, Ramos H. Numerical treatment of two-parameter singularly perturbed parabolic convection diffusion problems with non-smooth data. Math Meth Appl Sci. 2018; 41: 5359-5387.
10.1002/mma.5067
Web of Science® Google Scholar
18Das P. An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numer Algorithms. 2019; 81: 465-487.
10.1007/s11075-018-0557-4
Web of Science® Google Scholar
19 Kumar K, Pramod Chakravarthy P, Das P, Ramos H. A graded mesh refinement approach for boundary layer originated singularly perturbed time-delayed parabolic convection diffusion problems. Math Methods Appl Sci. 2021. doi:10.1002/mma.7358
10.1002/mma.7358
Web of Science® Google Scholar
20Yapman O, Amiraliyev G, Amirali G. Convergence analysis of fitted numerical method for a singularly perturbed nonlinear Volterra integro-differential equation with delay. J Comput Appl Math. 2019; 355: 301-309.
10.1016/j.cam.2019.01.026
Web of Science® Google Scholar
21Kudu M, Amirali G, Amiraliyev G. A finite-difference method for a singularly perturbed delay integro-differential equation. J Comput Appl Math. 2016; 308: 379-390.
10.1016/j.cam.2016.06.018
Web of Science® Google Scholar
22Erdogan F, Zhongdi C. A uniformly almost second order convergent numerical method for singularly perturbed delay differential equations. J Comput Appl Math. 2018; 333: 382-394.
10.1016/j.cam.2017.11.017
Web of Science® Google Scholar
23Erdogan F, Sakar M, Saldir O. A finite difference method on layer-adapted mesh for singularly perturbed delay differential equations. Appl Math Nonlinear Sci. 2020; 5(1): 425-436.
10.2478/amns.2020.1.00040
Web of Science® Google Scholar
24Kumar K, Pramod Chakravarthy P, Vigo-Aguiar J. Numerical solution of time-fractional singularly perturbed convection-diffusion problems with a delay in time. Math Methods Appl Sci. 2021; 44(4): 3080-3097.
10.1002/mma.6477
Web of Science® Google Scholar
25Das P, Rana S, Vigo-Aguiar J. Higher order accurate approximations on equidistributed meshes for boundary layer originated mixed type reaction diffusion systems with multiple scale nature. Appl Numer Math. 2020; 148: 79-97.
10.1016/j.apnum.2019.08.028
Web of Science® Google Scholar
26Das P, Rana S, Vigo-Aguiar J. A perturbation-based approach for solving fractional-order Volterra-Fredholm integro differential equations and its convergence analysis. Int J Comput Math. 2020; 97(10): 1994-2014.
10.1080/00207160.2019.1673892
Web of Science® Google Scholar
27Das P, Rana S, Vigo-Aguiar J. Homotopy perturbation method for solving Caputo-type fractional-order Volterra-Fredholm integro-differential equations. Comp Math Methods 12019; e1047: 1–9.
10.1002/cmm4.1047
CAS Google Scholar
28Lange C, Miura R. Singular perturbation analysis of boundary-value problems for differential-difference equations. SIAM J Appl Math. 1982; 42(3): 502-530.
10.1137/0142036
Web of Science® Google Scholar
29Roos H, Zarin H. The streameline-diffusion method for a convection-diffusion problem with a point source. J Comput Appl Math. 2003; 150: 109-128.
10.1016/S0377-0427(02)00568-X
Web of Science® Google Scholar
30Subburayan V, Ramanujam N. Uniformly convergent finite difference schemes for singularly perturbed convection diffusion type delay differential equations. Differ Equ Dyn Syst. 2021; 29(1): 139-155.
10.1007/s12591-018-00451-x
Web of Science® Google Scholar
31Senthilkumar L, Subburayan V. An improved initial value method for singularly perturbed convection diffusion delay differential equations. Adv Math Sci J. 2021; 10(2): 991-1001.
10.37418/amsj.10.2.28
Google Scholar
32Farrell P, Hegarty A, Miller J, O'Riordan E, Shishkin G. Singularly perturbed convection diffusion problems with boundary and weak interior layers. J Comput Appl Math. 2004; 166: 133-151.
10.1016/j.cam.2003.09.033
Web of Science® Google Scholar
33Subburayan V. A robust computational method for system of singularly perturbed differential difference equations with discontinuous convection coefficients. Int J Comput Methods 2016; 13(4): 1641008( 1–17).
10.1142/S0219876216410085
Web of Science® Google Scholar
34Miller J, O'Riordan E, Shishkin G. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions. World Scientific Publishing; 2012.
10.1142/8410
Google Scholar
35Avijit D, Natesan S. SDFEM for singularly perturbed boundary-value problems with two parameters. J Appl Math Comput. 2020; 64: 591-614.
10.1007/s12190-020-01370-3
Web of Science® Google Scholar

Citing Literature

All articles

An asymptotic streamline diffusion finite element method for singularly perturbed convection-diffusion delay differential equations with point source

Abstract

1 INTRODUCTION

2 PROBLEM STATEMENT

3 STABILITY AND ANALYTICAL RESULTS

4 ASYMPTOTIC EXPANSION APPROXIMATION

5 WEAK FORMULATIONS

5.1 Weak formulation of the problem (2)

5.2 Weak formulation of the problem (7)

6 FINITE ELEMENT FORMULATIONS

6.1 Mesh points and properties

6.2 The streamline diffusion finite element method for (8)

6.3 The streamline diffusion finite element method for (9)

7 ERROR ESTIMATES IN GENERAL SETUP

7.1 Interpolation error

7.2 Projection error

7.3 Consistency error

8 NUMERICAL EXAMPLE PROBLEMS

9 DISCUSSION

CONFLICT OF INTEREST

AUTHOR CONTRIBUTIONS

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An asymptotic streamline diffusion finite element method for singularly perturbed convection-diffusion delay differential equations with point source

Abstract

1 INTRODUCTION

2 PROBLEM STATEMENT

3 STABILITY AND ANALYTICAL RESULTS

4 ASYMPTOTIC EXPANSION APPROXIMATION

5 WEAK FORMULATIONS

5.1 Weak formulation of the problem (2)

5.2 Weak formulation of the problem (7)

6 FINITE ELEMENT FORMULATIONS

6.1 Mesh points and properties

6.2 The streamline diffusion finite element method for (8)

6.3 The streamline diffusion finite element method for (9)

7 ERROR ESTIMATES IN GENERAL SETUP

7.1 Interpolation error

7.2 Projection error

7.3 Consistency error

8 NUMERICAL EXAMPLE PROBLEMS

9 DISCUSSION

CONFLICT OF INTEREST

AUTHOR CONTRIBUTIONS

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information