SPECIAL ISSUE PAPER

Full Access

Invariant measure for continuous open chain of contours with discrete time

Corresponding Author

Marina V. Yashina

[email protected]

Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), Moscow, Russia

Department of Cybernetics and Information Technologies, Moscow Technical University of Communications and Informatics, Moscow, Russia

Correspondence Marina V. Yashina, Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), 64, Leningradsky Prospect, Moscow, Russia.

Email: [email protected]

Search for more papers by this author

Alexander G. Tatashev,

Alexander G. Tatashev

Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), Moscow, Russia

Department of Cybernetics and Information Technologies, Moscow Technical University of Communications and Informatics, Moscow, Russia

Search for more papers by this author

Marina V. Yashina,

Corresponding Author

Marina V. Yashina

[email protected]

Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), Moscow, Russia

Department of Cybernetics and Information Technologies, Moscow Technical University of Communications and Informatics, Moscow, Russia

Correspondence Marina V. Yashina, Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), 64, Leningradsky Prospect, Moscow, Russia.

Email: [email protected]

Search for more papers by this author

Alexander G. Tatashev,

Alexander G. Tatashev

Department of Higher Mathematics, Moscow Automobile and Road Construction State Technical University (MADI), Moscow, Russia

Department of Cybernetics and Information Technologies, Moscow Technical University of Communications and Informatics, Moscow, Russia

Search for more papers by this author

First published: 28 September 2021

https://doi.org/10.1002/cmm4.1197

Citations: 2

Share a link

Email
Wechat
Bluesky

Abstract

A dynamical system is studied. This system belongs to the class of contour networks introduced by A.P. Buslaev. The system is a version of the system called an open chain of contours. Continuous and discrete versions of the system were considered earlier. The system contains N contours. There is one adjacent contour for the utmost left and the utmost right contour, and there are two adjacent contours for any other contour. There is a common point of any two adjacent contours. This point is called a node. There is a cluster in each contour. For the continuous version, the cluster is a segment, moving with constant velocity if there is no delay. For the discrete version, the cluster is a group of adjacent particles. Delays are due to that two clusters may not move through the same node simultaneously. The main system characteristic, studied earlier, is the average velocity of clusters. In this paper, the continious and discrete version of the open chain of contours are considered. The following version of the system is also considered. Each cluster is a segment, and the cluster is shifted onto the distance α at any discrete moment if no delay occurs. We have obtained the limit distribution of the system states. We have also obtained the limit state distribution (invariant measure) for the open chain of contours with continuous state space and continuos time and for the open chain of contours with discrete state space and discrete time.

1 INTRODUCTION

In a class of transport models, the traffic is modeled by the movement of particles on a cellular field. These models may be interpreted in terms of cellular automata¹ or exclusive processes.² For simple cases, analytical results are obtained in References 3-9. The behavior of a model of this type is an asymmetrical simple exclusive process. In the models, considered in these articles, the particles move on a closed or infinite one-dimensional lattice. The article¹⁰ studies a one-dimensional model, which is a dynamical system with a continuous state space and discrete time. In particular cases, the system behavior is identical with the behavior of the models considered in References 3-6. In Reference 10 an exclusive process with discrete time is called synchronous, and an exclusive process with continuous time is called asynchronous.

The article¹¹ studies a one-dimensional traffic model with particles of different types. In this model, particles can move forward and backward. In Reference 11, a version with discrete time and a version with continuous time are considered. The behavior of the version with discrete time is a synchronous exclusive process (in terms of Reference 10). The behavior of the version with continuous time is an asynchronous exclusive process. In Reference 11, the discrete time model is interpreted as a discrete time queuing network as in Reference 7, and the continuous time model is interpreted as a continuous time queuing network, Figure 1. Formulas for the average velocity of particles are obtained. The traffic models, considered in Reference 11, can be used with the deterministic-stochastic approach to traffic modeling. The deterministic-stochastic approach was introduced in References 12, 13.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

A discrete queuing network related to the traffic model

A model with movement of particles on a two-dimensional toroidal lattice was studied in References 14, 15.

In Reference 16 stability conditions for a controlled dynamical system were obtained. In Reference 17 a continuous dynamical system obtained by considering the discrete original model in continuous time. While the dynamics of the continuous model is trivial, it is possible to recover the complexity of the discrete model by the introduction of time delays. In particular, high period limit cycles and chaotic attractors are observed.

The concepts of cluster movement and contour network were introduced by Buslaev.^{18, 19} This concept was introduced to obtain analytical results for traffic models with network structure. There may be also other applications of contour networks. For example, the concept of contour networks can be used to analyse communications systems. In a discrete traffic model with cluster movement, particles, located in adjacent cells, form clusters, and the particles of the same cluster move simultaneously. In a continuous version, a cluster is a segment moving with constant velocity, Figure 2.

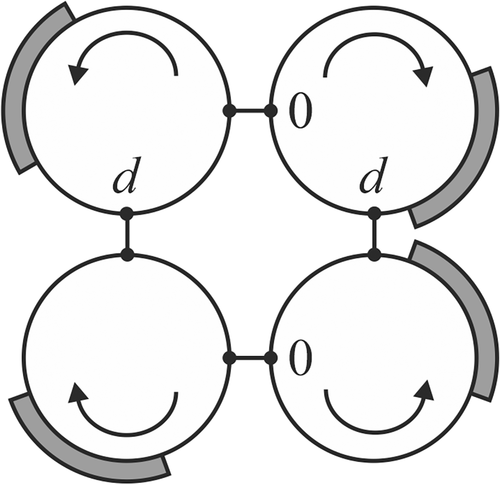
A contour network contains a system of contours. There are common points of adjacent contours called nodes. In contours, particles or clusters move. Delays occur at the nodes. These delays are due to that no more than one particle (cluster) can pass through the same node simultaneously. The movement of particles on a contour is deterministic but the rule under which particles pass through the node can be stochastic. The stochastic movement can become deterministic from a moment if from this moment no delays occur. The main characteristic of contour system is the average velocity taking into account the delays. In References 19-34 , the limit cycles and values of average velocities, depending of the initial state of the system, are obtained for some deterministic systems with two contours and contour networks with regular structures. For the contour networks that were considered in References 19-34, both the state space and time scale are discrete, both the state space and time scale are continuous. States of a deterministic discrete contour network are repeated from a moment. Thus a limit cycle of the dynamical system is realized. If the length of each contour of a deterministic continuous contour network is the same, then the invariant state sets of the system are also limit cycles. An important problem is to find the set of limit cycles.

In Reference 21, a dynamical system called a closed chain of contours (or necklace) is introduced. The closed chain of contours is a dynamical system with a one-dimensional structure, Figures 3 and 4. There are two adjacent contours for any contour of the closed chain of contours. One of the adjacent contours is located on the left, and the other adjacent contour is located on the right. There is a common node for any two adjacent contours. If two particles try to move through a node simultaneously, then a competition occurs and only one of the competing particles moves at present moment. Closed chains with different resolution rules are studied in References 19, 21, 25, 26, 29, 30. In Reference 19, the continuous and discrete versions were introduced. In the discrete version the nodes are located between cells. In References 19, 21, 26, 29, analytical results for the discrete version are obtained. In particular, in References 19, 21, 29, analytical results are obtained under the assumption that there are two cells and a particle in any contour (a binary chain). In Reference 25, analytical results for the continuous version of closed chain of contours are obtained.

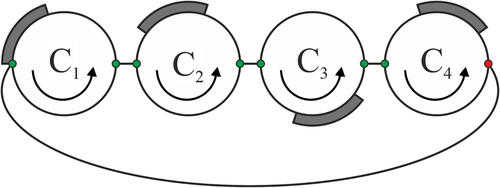
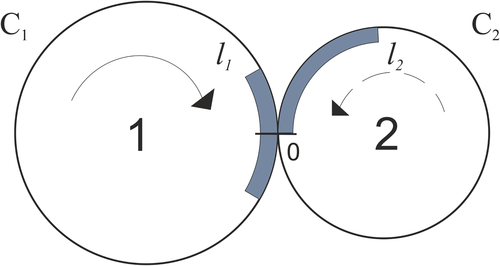
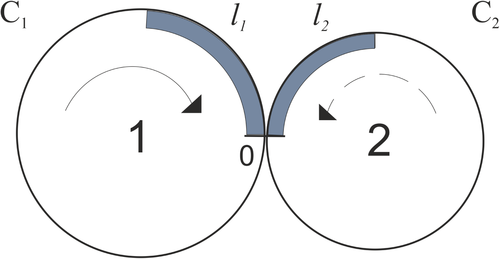
In References 27, 28, a dynamical system called an open chain of contours is considered. In this system, the utmost left or the utmost right contour has a node such that this node is common for this contour and the adjacent contour. There are two adjacent contours and two nodes for any other contour. In Reference 27, the continuous version of open chain of contours is studied, and, in Reference 28, the discrete version is studied. In References 27, 28, the limits cycles and values of the average velocity are obtained.

In Reference 19, a dynamical system with two-dimensional toroidal structure is also introduced. This system is called a chainmail. There are four adjacent contours for each contour of chainmail. In Reference 20, the chainmail is studied under the assumption that there are four cells and a particle in any contour of chainmail. There are four adjacent contours for any contour of chainmail. Any cell is combined with the node which is common for two contours. Analytical results for this system were obtained in Reference 22. A version of the chainmail with rectangular structure (open chainmail) was also considered.

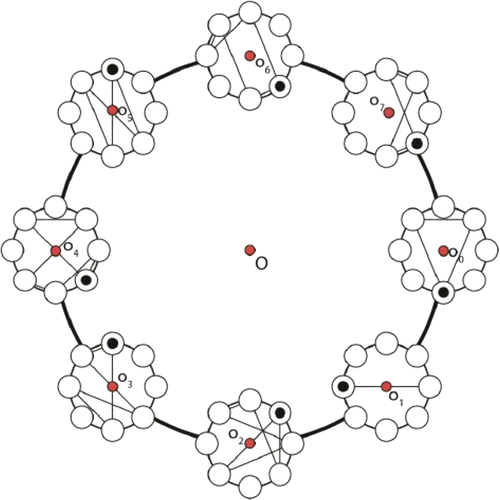
Some contours networks with two-dimensional honeycomb structure were studied in Reference 22, Figure 5.

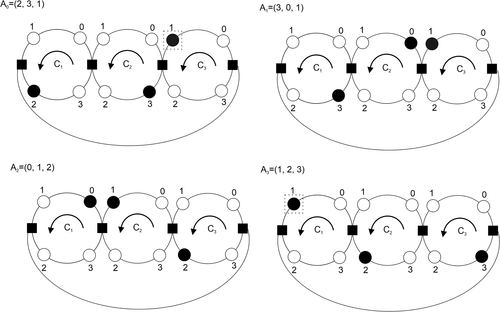
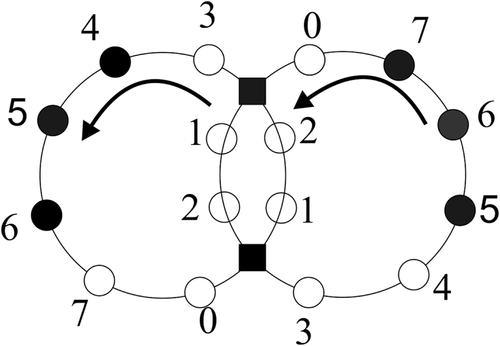
The article²⁴ studies different discrete versions of the contour network with two contours and a common node (two-contours system). In the system, the particles move under rules similar to the rules of the elementary cellular automaton 184 or 240. The rule 240 corresponds to the cluster movement in a discrete contour network. The article³² considers a continuous two-contours with contours of different lengths, Figures 6 and 7. Some concepts and theorems of the number theory are used to analyse this system. If the ratio of the contours is a rational number, then limit cycles are realized. If the ratio of the contours is an irrational number, then the invariant state space of the system is a spectral cycle only if the system does not result in a state of free movement. The article³¹ studies a contour network with two contours and two common nodes is studied, Figure 8. The article³³ studies a contour network with two contours of different lengths and one common node. It is assumed in Reference 33 that the particles move under the rule similar to the rule similar to the rule of the elementary cellular automaton 184.

In References 35-37 dynamical systems similar to the contour networks are considered. In Reference 35, some dynamical systems are considered which can be interpreted as follows. There is a set of vertices. At discrete moment, each vertex can send messages to other vertices through channels connecting the vertices. The vertices send the messages under a prescribed plan. Delays in the transmission of messages are due to that no more than one message can be transmitted simultaneously through the same channel. In particular cases, the behavior of the system can be represented by the same process as a related contour network. In Reference 35, a stochastic version is introduced for a system of this type. If the system is in the state such that, in the deterministic version, a message is transmitted (or a particle moves), then the probability that, in the stochastic version, the message is transmitted (the particle moves) is $1 - ε,$ where $ε$ is a small value. The asymptotic behavior of the system as $ε \to 0$ is studied.

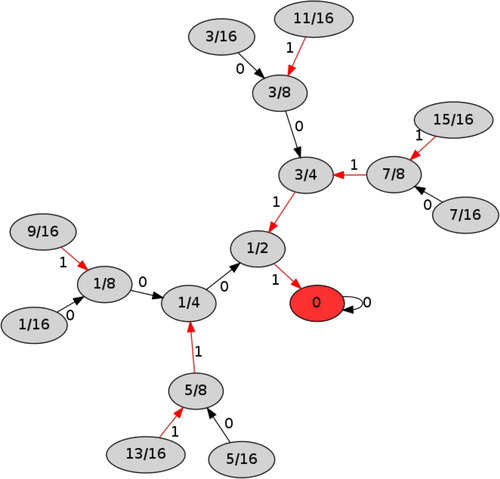
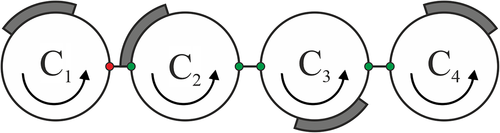
The articles^36-38 study dynamical systems such that particles move in channels of these system under prescribed plans. In particular, a dynamical system called a bipendulum is studied, Figure 9. The bipendulum contains two vertices. The vertices send messages to each other through channel under a prescribed plan. The plan of a particle is prescribed by the sequence of digits in the binary representation of a real number. Delays in the plan realization are due to that particles cannot move through the channel in the opposite directions simultaneously. If the particles try to move in the opposite directions simultaneously, then a competition occurs, and only the particle winning the competition moves at the present moment. Each of two competing particles wins the competition equiprobably. A Markov chain is related to the system. If the plans of the particles are prescribed by rational numbers, then there exist the stationary probabilities of this Markov chain. Some algebraic concepts and classical theorems of the number theory are used to analyse the behavior of bipendulum. In Reference 36, a class of unary algebras is introduced for analysing the bipendulum. These algebras are defined on the set of the rational numbers belonging to the segment $[0, 1] .$ There is a unique unary operation in a algebra of this type. This operation is called the Bernoulli shift. Therefore these algebras are called the Bernoulli algebras. The article³⁷ studies a generalization of the bipendulum called a real valued pendulum, Figure 10. The system is developed for modeling of particles relocations on abstract graph with formalized rules of behavior (competition for space) and movement plans logistics. Logistics is given in a formal statement by the real numbers of the unit closed interval, presented in calculus with base equals to the graph power $N .$

The main problem is to study the behavior of the pendulum depending on its architecture.

A generalization of the class of Bernoulli algebras can be used for analysing the real-valued pendulum. This generalization is studied in Reference 39. The article³⁸ also studies some other dynamical systems similar to the real-valued pendulum, in particular, the system called a chaotic pendulum.

An open chain of the contours with continuous state space and discrete time is introduced in this article. The limit state distribution of this system is obtained. This system is a generalization of a dynamical system called circumference shifts, which was considered in Reference 40.

2 THE SYSTEM WITH CONTINUOUS STATE SPACE AND CONTINUOUS TIME

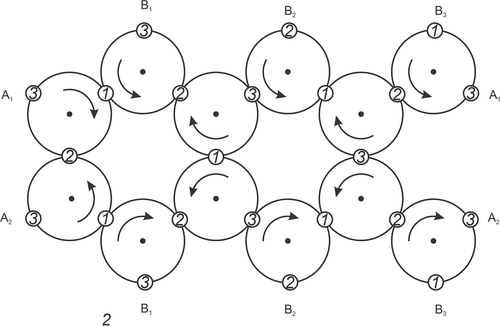
Let a dynamical system contain N circumferences (contours) $1, 2, \dots, N,$ Figure 11. The coordinate system $[0, 1)$ is defined on each circumference. There is a common point of the circumferences i and $i + 1 .$ This point is called the node $(i, i + 1) .$ The coordinate of the node $(i, i + 1)$ equals 0 for the circumference $i,$ and the coordinate of the node $(i, i + 1)$ equals $1 / 2$ for the circumference $i + 1,$ $i = 1, 2, \dots, N - 1 .$ There is a segment, called a cluster on each circumference. The length of the cluster equals $l < 1 .$ A state of the system is the vector $x = (x_{1}, \dots, x_{N}),$ where $x_{i}$ is the coordinate of the leading point of the cluster, located on the circumference $i,$ (cluster $i),$ $i = 1, \dots, N .$ We say that the cluster i occupies the node $(i, i + 1)$ if $0 < x_{i} < l,$ $i = 1, 2,, \dots, N - 1 .$ We say that the cluster i occupies the node $(i - 1, i)$ if $\frac{1}{2} < x_{i} < \frac{1}{2} + l,$ and, for $l > \frac{1}{2},$ also if $0 < x_{i} < l - \frac{1}{2},$ $i = 2, 3, \dots, N .$ The state of the system is admissible if no node is occupied by more than one cluster. The initial state, that is, the state of the system at time $t = 0,$ is prescribed. Let $S^{N}$ be the set of admissible states. At any time, each cluster moves with the velocity 1 if there is no delay. The delay of a cluster occurs if this cluster is at the node occupied by the cluster of the adjacent contour. If the clusters i and $i + 1$ come to the node $(i, i + 1)$ simultaneously, then the cluster i passes through the node first. This system is called the system $A_{0}^{N} .$

The system state at time t is the N-tuple $(x_{1} (t), \dots, x_{N} (t)),$ where $x_{i} (t)$ is the coordinate of the leading point of the cluster i at this time, $i = 1, \dots, N .$

Let an arc be defined on any circle. Denote by $Δ_{i}$ the arc located on the circumference $i,$ $i = 1, 2, \dots, N .$ Let $Δ = Δ_{1} \times Δ_{2} \times \dots \times Δ_{N}$ be the Cartesian product of the arcs. Denote by $H_{Δ} (t, x_{0})$ the total time in the interval $(0, t)$ such that during this time the system is in states of the set $Δ \cap S^{N}$ for the initial state $x_{0} .$

Suppose

F_{Δ} (x_{0}) = \lim_{t \to \infty} \frac{H_{Δ} (t, x_{0})}{t} .

Suppose that the initial state

x_{0}

is prescribed. A generalized function

f (x_{1}, \dots, x_{N})

is called the limit state distribution density if, for any

Δ \in S^{N},

F_{Δ} (x_{0}) = \int_{Δ} f (x_{1}, \dots, x_{N}) d x_{1} \dots d x_{N} .

()

Let

δ_{i}

be the Dirac delta function and

[a]

be the integral part of the number

a .

Theorem 1.For any initial state, the limit density $f (x_{1}, \dots, x_{N})$ is not equal to 0 if and only if, there exist $t,$ $i_{0},$ $i_{1}$ such that $0 \leq t < (N - 1) l - \frac{N}{2} + 1,$

i_{0} = [\frac{t}{l - \frac{1}{2}}], i_{1} = \max ([\frac{t - \frac{1}{2}}{l - \frac{1}{2}}], 0),

0 \leq x_{N - i_{0}} = t - i_{0} (l - \frac{1}{2}) < l - \frac{1}{2},

and

f (x_{1}, \dots, x_{N}) = \frac{1}{2 (N - 1) l - N + 2} \cdot \prod_{i = 1}^{N - i_{0} - 1} δ (x_{i}) \times

\times \prod_{i = N - i_{0} + 1}^{N - i_{1}} δ (x_{i} - x_{N - i_{0}} - (i - N + i_{0}) (l - \frac{1}{2})) \cdot \prod_{i = N - i_{1} + 1}^{N} δ (x_{i} - \frac{1}{2}),

or there exist

t,

i_{0},

i_{1}

such that

0 \leq t < (N - 1) l - \frac{N}{2} + 1,

i_{0} = [\frac{t}{l - \frac{1}{2}}], i_{1} = \max ([\frac{t - \frac{1}{2}}{l - \frac{1}{2}}], 0),

\frac{1}{2} \leq x_{i_{0} + 1} = \frac{1}{2} + t - i_{0} (l - \frac{1}{2}) < l,

and

f (x_{1}, \dots, x_{N}) = \frac{1}{2 (N - 1) l - N + 2} \cdot \prod_{i = 1}^{i_{1}} δ (x_{i}) \times

\times \prod_{i = i_{1} + 1}^{i_{0} - 1} δ (x_{i} - x_{i_{0} + 1} - (i_{0} + 1 - i) (l - \frac{1}{2})) \cdot \prod_{i = i_{0} + 2}^{N} δ (x_{i} - \frac{1}{2})

b < a,

then it is assumed that

\prod_{a}^{b} = 1 .

Proof.In accordance with results obtained in Reference 27 , from any initial state, the system results in the state $(0, 0, \dots, 0),$ and, further, the system states are repeated with period $T = 2 (N - 1) l - N + 2$

Suppose, at $t = 0,$ the system is in the state $(0, 0, \dots, 0) .$ Let us consider the behavior of the system in time interval $(0, (N - 1) l - \frac{N}{2} + 1) .$ In the time interval $(0, l - \frac{1}{2}),$ only the cluster N moves. The cluster $N - i$ begins to move at time $t = i (l - \frac{1}{2})$ and ends to move at time $t = i (l - \frac{1}{2}) + \frac{1}{2} .$ At time $t = (N - 1) l - \frac{N}{2} + 1,$ the system results in the state $(\frac{1}{2}, \frac{1}{2}, \dots, \frac{1}{2}) .$ Hence, the following is true.

Suppose

t \in (0, (N - 1) l - \frac{N}{2} + 1),

i_{0} (t) = [\frac{t}{l - \frac{1}{2}}], i_{1} (t) = \max ([\frac{t - \frac{1}{2}}{l - \frac{1}{2}}], 0) .

Then, at time

t,

the clusters

1, \dots, N - i_{0} - 1

do not move, and

x_{1} (t) = \dots = x_{N - i_{0}} (t) = 0,

()

the clusters

N - i_{0}, \dots, N - i_{1}

move, and

x_{i} = x_{N - i_{0}} - (i - N + i_{0}) (l - \frac{1}{2}), i = N - i_{0}, i_{0} + 1, \dots, N - i_{1},

()

and the clusters

N - i + 2, \dots, N

do not move,

x_{N - i_{1} + 2} = \dots = x_{N} = \frac{1}{2} .

()

Suppose, at time $t = 0,$ the system is in the state $(\frac{1}{2}, \dots, \frac{1}{2}) .$ Suppose

t \in (0, (N - 1) l - \frac{N}{2} + 1), i_{0} (t) = [\frac{t}{l - \frac{1}{2}}],

i_{1} (t) = \max ([\frac{t - \frac{1}{2}}{l - \frac{1}{2}}], 0) .

Then, at time

t,

the clusters

1, \dots, i_{1}

do not move,

x_{1} = \dots = x_{i_{1}} = 0,

()

the clusters

i_{1} + 1, \dots, i_{0}

move, and

x_{i} = x_{i_{0} + 1} + (i_{0} + 1 - i) (l - \frac{1}{2}),

()

the clusters

i_{0} + 2, \dots, N

do not move, and

x_{i_{0} + 1} = \dots = x_{N} = \frac{1}{2} .

()

Using (2)–(7), we get Theorem 1.

3 SYSTEM WITH CONTINUOUS STATE SPACE AND DISCRETE TIME

We shall consider the system, considered in Section 2, as a system with discrete time. We fix the system states at moments

t_{i} = i α,

where

α

is a prescribed number,

i = 0, 1, 2, \dots

The state

y = (y_{1}, \dots, y_{N})

at time

t_{i}

is the map

G_{α} (x)

such that this map takes the state

x = (x_{1}, \dots, x_{N})

at time

t_{i - 1}

to the state

y = (y_{1}, \dots, y_{N})

at time

t_{i},

i = 1, 2, \dots :

y = (y_{1}, \dots, y_{N}) = G_{α} (x_{1}, \dots, x_{N}) .

The new system is called the system

A_{α}^{N} .

Let the map

G_{α}^{k} (x)

be the k-fold composition of the map

G_{α}

x = (x_{1}, \dots, x_{N}) .

Denote by

Δ = Δ_{1} \times \dots \times Δ_{N}

the Cartesian product of N arcs, and the ith arc is defined on the circumference

i,

i = 1, \dots, N .

Suppose,

Δ \cap S_{0}^{N},

F_{Δ} (x, n) = card \{k : 0 \leq k < n, G_{α}^{k} (x) \in Δ \cap S_{0}^{N}\} .

The state distribution density

f (x_{1}, \dots, x_{N})

is defined for the system considered in Section 2. Namely, the state distribution density satisfies 1.

Theorem 2.

(1)
Let the ratio $α$ and l be an irrational number. Then the state distribution densities for the system $A_{α}^{N}$ and the corresponding system with continuous time (we call it the system $A_{0}^{N}$ )are the same, that is, these densities correspond to Theorem 1.
(2)
If the ratio $α$ and l is a rational number, then the limit state distribution is discrete.

Proof.In Reference 40, a dynamical system, which we call the system $A_{α}^{1},$ is considered. The set of the system states is $[0, 1) .$ The initial state $x (0)$ is prescribed. The system state at time $t + 1$ is

x (t + 1) = x (t) + α

()

(addition modulo 1).

In Reference 1 it has been proved that, if the number $α$ is irrational, then the limit state distribution of the system $A_{α}^{1}$ is uniform.

Suppose that, at the initial moment $t = 0,$ the systems $A_{0}^{N}$ and $A_{α}^{N}$ are in the same state. It follows from the results of Reference 20, for the system $A_{0}^{N},$ there exist $i_{0}$ such that, at time $t_{i_{0}} = i_{0} α,$ the system is in a state belonging to a periodic orbit (limit cycle) with period

T = 2 (N - 1) l - N + 2 .

Let this system be in the state x belonging to a limit cycle. At time

t_{i_{0}},

the system

A_{α}^{N}

will be also in the state

x .

Let x be the new initial state of the systems

A_{0}^{N}

and

A_{α}^{N} .

Let $Δ (t, t + δ)$ be the set of system $A_{0}^{N}$ states such that the system $A_{0}$ is in the state in time interval $(t, t + δ),$ $0 \leq t < t + δ,$ $o \leq t < t + δ,$ $0 \leq t < t + δ \leq T$ greater than t and less than $t + δ$ time units. Suppose

F_{0}^{N} (t, t + δ) = \lim_{B \to \infty} \frac{H (t, t + δ, B)}{B},

where

H (t, t + δ, B)

is the total time such that the system is in the set

Δ (t, t + δ)

during the time interval

(0, B) .

Analogously, we define the value $F_{α}^{N} (t, t + δ)$ as the part of time such that during this time the system $A_{α}^{N}$ is in the states of the set $(t, t + δ)$ , and we define the value $F_{α}^{1} (t, t + δ)$ as the part of time such that, during this time, the system $A_{α}^{1}$ is in the states, belonging to the set $(\frac{t}{T}, \frac{t + δ}{T}) .$ It is evident that

F_{α}^{N} (t, t + δ) = F_{α}^{1} (t, t + δ) = F_{0}^{N} (t, t + δ) = \frac{δ}{T} .

This proves the first statement of the theorem.

The second statement of the theorem follows from that, as it has been proved in Reference 1,

F_{α}^{N} (t, t + δ) = F_{α}^{1} (t, t + δ),

and, if

α

is rational number, the limit state distribution for the system

A_{α}^{1}

is discrete and Theorem 2 has been proved.

4 CONCLUSION

The article considers two versions of a dynamical system called an open chain of contours which belongs to a class of Buslaev contour networks. The contour networks were developed to obtain analytical results for traffic models with network structures. The contour networks can also have other applications. Analytical results were obtained for the two-contour systems and contour networks with regular structure.

Earlier, results were obtained for contour networks with both a discrete state space and discrete time, and results were also obtained for contour networks with both a continuous state space and continuous time. Contour networks with continuous state space and discrete time were not considered. A contour system of such type is considered in this article. The article considers two versions of open chain of contours. The utmost left and the utmost right contour of an open chain has only one adjacent contour. Each of the others contours of the system has two adjacent contours.

The first considered version of the open chain is a system with a continuous state space and continuous time. The new result is that the stationary state distribution (invariant measure) has been obtained.

The second version is an open chain with a continuous state space and discrete time, which is a generalization of a dynamical system called circumference shifts, which was considered by A. Katok and B. Hasselblatt. For this version of open chain, the stationary state distribution is also obtained. This invariant measure does not depend on the initial state of the system, though, for other contour networks, for example, closed chains of contours, the invariant measure can depend on the initial state.

ACKNOWLEDGMENT

The work is supported by the Russian Foundation for Basic Research (project No. RFBR 20-01-00222)

Biographies

Marina V. Yashina is professor and a head of Higher Mathematics Department of the Moscow Automobile and Road Construction Technical University (Russia), and a professor of Mathematical Cybernetics and IT Department of the Moscow Technical University of Communications and Informatics (Russia). From 1974 till 1979 she is an undergraduate student of the Lomonosov Moscow State University, Mechanical-Mathematical Faculty (Russia). She received her PhD (Math) degree from the Lomonosov Moscow State University (Russia) in 1989, and Dr. Sc. (Tech.) from the Moscow Automobile and Road Construction Technical University (Russia) in 2000. Her research has mainly focused on dynamical systems, mathematical modeling of complex socio-technical systems, intelligent transport systems, and cybernetics.
Alexander G. Tatashev was born on February 15, 1955 in Moscow, Russia. From 1973 till 1978 he is an undergraduate student of Moscow Physical Technical Institute, Russia. From 1978 till 1995 he worked at Scientific Research Institute of Communications and Control Systems. From 1995 till present he works at Moscow Automobile and Road Technical University. From 2003, he is professor of this university. He is the author more than 100 research publications related to queuing theory, mathematical modeling, discrete dynamical systems et al.

REFERENCES

1Wolfram S. Statistical mechanics of cellular automata. Rev Mod Phys. 1983; 55(3): 601-644. doi:10.1103/RevModPhys.55601
10.1103/RevModPhys.55.601
Web of Science® Google Scholar
2 Spitzer F. Interaction of Markov processes. In Random Walks, Brownian Motion, and Interacting Particle Systems. Birkhäuser, Boston, MA; 1991; 66-110.
Google Scholar
3Schreckenberg M, Schadschneider A, Nagel K, Ito N. Discrete stochastic models for traffic flow. Phys Rev E. 1995; 51(4): 2939-2949. doi:10.1103/PhysRevE.51.2939
10.1103/PhysRevE.51.2939
CAS Web of Science® Google Scholar
4Blank ML. Exact analysis of dynamical systems arising in models of traffic flow. Russ Math Surv. 2000; 55(3): 562. doi:10.1070/RM2000v055n03ABEH000295
10.1070/RM2000v055n03ABEH000295
Web of Science® Google Scholar
5Belitsky V, Ferrari PA. Invariant measures and convergence properties for cellular automaton 184 and related processes. J Stat Phys. 2005; 118(3): 589-623. doi:10.1007/s10955-044-8822-4
10.1007/s10955-004-8822-4
Web of Science® Google Scholar
6Blank M. Dynamics of traffic jams: order and chaos. Mosc Math J. 2001; 1(1): 1-26. doi:10.17323/1609-4514-2001-1-1-1-26
10.17323/1609-4514-2001-1-1-1-26
Web of Science® Google Scholar
7Kanai M, Nishinari K, Tokihiro T. Exact solution and asymptotic behaviour of the asymmetric simple exclusion process on a ring. J Phys A Math Gen. 2006; 39(29): 9071-9079. 10.1088/0305-4470/39/29/004
10.1088/0305-4470/39/29/004
Google Scholar
8Gray L, Griffeath D. The ergodic theory of traffic jams. J Stat Phys. 2001; 105(3): 413-452. doi:10.1023/A:1012202706850.
10.1023/A:1012202706850
Web of Science® Google Scholar
9Kanai M. Two-lane traffic-flow model with an exact steady-state solution. Phys Rev E. 2010; 82:066107. doi:10.1103/PhysRevE.82.066107
10.1103/PhysRevE.82.066107
PubMed Web of Science® Google Scholar
10Blank M. Metric properties of discrete time exclusion type processes in continuum. J Stat Phys. 2010; 140(1): 170-197. doi:10.1007/s10955-010-9983-y
10.1007/s10955-010-9983-y
CAS Web of Science® Google Scholar
11Yashina M, Tatashev A. Traffic model based on synchronous and asynchronous exclusion processes. Math Methods Appl Sci. 2020; 43(14): 8136-8146. doi:10.1002/mma.6237
10.1002/mma.6237
Web of Science® Google Scholar
12Lukanin V, Buslaev A, Novikov A, Yashina M. Traffic flows modelling and the evaluation of energy-ecological parameters. Part I. Int J Veh Des. 2003; 33(4): 381-399. doi:10.1504/LJVD.2003.003578
10.1504/IJVD.2003.003578
Web of Science® Google Scholar
13Lukanin V, Buslaev A, Novikov A, Yashina M. Traffic flows modelling and evaluation of energy-ecological parameters. Part II. IntJ of Vehicle Design. 2003; 33(4): 400-421. doi:10.1504/LJVD.2003.003577
10.1504/IJVD.2003.003577
Web of Science® Google Scholar
14Biham O, Middleton AA, Levine D. Self-organization and a dynamical transition in traffic-flow models. Phys Rev A. 1992; 46(10): R6124. doi:10.1003/PhysRevA.46.R6124
10.1103/PhysRevA.46.R6124
CAS PubMed Web of Science® Google Scholar
15Angel O, Holroyd A, Martin J. The jammed phase of the Biham-Middleton-Levine traffic model. Electron Commun Probab. 2005; 10: 167-178. doi:10.1214/ECP.v10-1148
10.1214/ECP.v10-1148
Web of Science® Google Scholar
16Čermák J, Jánskỳ J, Matsunaga H. On stability and stabilization of some discrete dynamical systems. Math Methods Appl Sci. 2018; 41(10): 3684-3695. doi:10.1002/mma.4855
10.1002/mma.4855
Web of Science® Google Scholar
17Caraballo T, Colucci R, Guerrini L. Dynamics of a continuous Henon model. Math Methods Appl Sci. 2018; 41(10): 3934-3954. doi:10.1002/mma.4878
10.1002/mma.4878
Web of Science® Google Scholar
18Bugaev AS, Buslaev AP, Kozlov VV, Yashina MV. Distributed problems of monitoring and modern approaches to traffic modeling. Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC); 2011:477-481. 10.1109/ITSC.2011.6082805
Google Scholar
19Kozlov V, Buslaev A, Tatashev A. On synergy of totally connected flows on chainmails. Proc. of the 13 International Conference on Computational and Mathematical Methods in Science and Engineering CMMSE-2013; Vol. 3, 2013:861-874.
Google Scholar
20Buslaev A, Tatashev A, Yashina M. Qualitative properties of dynamical system on toroidal chainmail. AIP Conf Proc. 2013; 1558(1): 1144-1147. 10.1063/1.4825710
10.1063/1.4825710
Google Scholar
21Kozlov VV, Buslaev AP, Tatashev AG. Monotonic walks on a necklace and a coloured dynamic vector. Int J Comput Math. 2015; 92(9): 1910-1920.
10.1080/00207160.2014.915964
Web of Science® Google Scholar
22Kozlov VV, Buslaev AP, Tatashev AG, Yashina MV. Dynamical systems on honeycombs. Traffic and Granular Flow. Springer; 2015: 441-452 10.1007/978-3-319-10629-8_49
Google Scholar
23Buslaev AP, Tatashev AG, Yashina MV. About synergy of flows on flower. Proceedings of the International Conference on Dependability and Complex Systems; 2016:7-84; Springer, Cham.
Google Scholar
24Buslaev AP, Tatashev AG. Exact results for discrete dynamical systems on a pair of contours. Math Methods Appl Sci. 2018; 41(17): 7283-7294. doi:10.1002/mma.4822
10.1002/mma.4822
Web of Science® Google Scholar
25Buslaev AP, Tatashev AG, Yashina MV. On flows spectrum on closed trio of contours with uniform load. Eur J Pure Appl Math. 2018; 11(1): 260-283. doi:10.29020/nybg.ejpam.v11i1.3201
10.29020/nybg.ejpam.v11i1.3201
Web of Science® Google Scholar
26Buslaev AP, Fomina MJ, Tatashev AG, Yashina MV. On discrete flow networks model spectra: statements, simulation, hypotheses. J Phys Conf Seri. 2018; 1053(1): 012034. doi:10.1088/1742/6596/1053/1/012034
10.1088/1742-6596/1053/1/012034
Google Scholar
27Buslaev AP, Tatashev AG. Spectra of local cluster flows on open chain of contours. Eur J Pure Appl Math. 2018; 11(3): 628-644. doi:10.29020/nybg.ejpam.v.11i3.3292.
10.29020/nybg.ejpam.v11i3.3292
Web of Science® Google Scholar
28Yashina M, Tatashev A. Discrete Open Buslaev chain with Heterogenous loading. 2019 7th International Conference on Control, Mechatronics and Automation; 2019:283-288; IEEE. 10.1109/ICCMA46720.2019.8988654
Google Scholar
29Tatashev A, Yashina M. Spectrum of elementary cellular automata and closed chains of contours. Mach Des. 2019; 7(2): 28. doi:10.3390/machines7020028
10.3390/machines7020028
Web of Science® Google Scholar
30 Buslaev A, Tatashev A, Yashina M. Flow spectrum of closed/open contours chains. Comput Math Methods. 2021;e1087. doi:10.1002/cmm4.1087
Google Scholar
31Yashina MV, Tatashev AG. Spectral cycles and average velocity of clusters in discrete two-contours system with two nodes. Math Methods Appl Sci. 2020; 43(7): 4303-4316. doi:10.1102/mma6194
10.1002/mma.6194
Web of Science® Google Scholar
32Myshkis P, Tatashev A, Yashina M. Cluster motion in a two-contour system with priority rule for conflict resolution. J Comput Syst Sci Int. 2020; 59(3): 311-321. doi:10.1134/s1064230720030119
10.1134/S1064230720030119
Web of Science® Google Scholar
33Tatashev A, Yashina M. Self-organization of two-contours dynamical system with common node and cross movement. WSEAS Trans Math. 2020; 18: 373-378.
Google Scholar
34Kozlov VV, Buslaev AP, Tatashev AG. A dynamical communication system on a network. J Comput Appl Math. 2015; 275: 247-261. doi:10.1016/j.cam.2014.07.026
10.1016/j.cam.2014.07.026
Web of Science® Google Scholar
35Buslaev AP, Yashina MV. On holonomic mathematical F-bipendulum. Math Methods Appl Sci. 2016; 39(7): 4820-4828. doi:10.1002/mma.3810
10.1002/mma.3810
Web of Science® Google Scholar
36Buslaev AP, Tatashev AG. Bernoulli algebra on common fractions and generalized oscillations. J Math Res. 2016; 8(3): 82-93.
10.5539/jmr.v8n3p82
Google Scholar
37Buslaev AP, Tatashev AG. On dynamical systems for transport logistic and communications. J Math Res. 2016; 8(4): 195-210. doi:10.5539/jmr.v8n4p195
10.5539/jmr.v8n4p195
Google Scholar
38 Kozlov VV, Buslaev AP, Tatashev AG. On real-valued oscillations of a bipendulum. Appl Math Lett. 2015; 46: 44-49. doi:10.1016/j/1016/j.aml.2015.02.00
10.1016/j.aml.2015.02.003
Web of Science® Google Scholar
39Buslaev AP, Tatashev AG, Yashina MV. On irrational oscillations of a bipendulum. Proceedings of the 10th International Conference on Dependability and Complex Systems, DepCos-RELCOMEX; Vol. 365, 2015:57-63. 10.1007/978-3-319-19216-1_6
Google Scholar
40Hasselblatt B, Katok A. A First Course in Dynamics: with a Panorama of Recent Developments. Cambridge University Press; 2003 10.1017/CBO9780511998188
10.1017/CBO9780511998188
Google Scholar

Citing Literature

All articles

Invariant measure for continuous open chain of contours with discrete time

Abstract

1 INTRODUCTION

2 THE SYSTEM WITH CONTINUOUS STATE SPACE AND CONTINUOUS TIME

3 SYSTEM WITH CONTINUOUS STATE SPACE AND DISCRETE TIME

4 CONCLUSION

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Invariant measure for continuous open chain of contours with discrete time

Abstract

1 INTRODUCTION

2 THE SYSTEM WITH CONTINUOUS STATE SPACE AND CONTINUOUS TIME

3 SYSTEM WITH CONTINUOUS STATE SPACE AND DISCRETE TIME

4 CONCLUSION

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information