Volume 3, Issue 6 e1195

RESEARCH ARTICLE

Full Access

Numerical approximations for a class of nonlinear higher order singular boundary value problem by using homotopy perturbation and variational iteration method

Biswajit Pandit,

Biswajit Pandit

Department of Mathematics, Indian Institute of Technology Patna, Patna, India

Search for more papers by this author

Amit Kumar Verma,

Amit Kumar Verma

Department of Mathematics, Indian Institute of Technology Patna, Patna, India

Search for more papers by this author

Ravi P. Agarwal,

Corresponding Author

Ravi P. Agarwal

[email protected]

Department of Mathematics, Texas A & M, University-Kingsville, Kingsville, Texas, USA

Correspondence Ravi P. Agarwal, Department of Mathematics, Texas A & M, University-Kingsville, 700 University Blvd., MSC 172, Kingsville, TX 78363-8202, USA.

Email: [email protected]

Search for more papers by this author

Biswajit Pandit,

Biswajit Pandit

Department of Mathematics, Indian Institute of Technology Patna, Patna, India

Search for more papers by this author

Amit Kumar Verma,

Amit Kumar Verma

Department of Mathematics, Indian Institute of Technology Patna, Patna, India

Search for more papers by this author

Ravi P. Agarwal,

Corresponding Author

Ravi P. Agarwal

[email protected]

Department of Mathematics, Texas A & M, University-Kingsville, Kingsville, Texas, USA

Correspondence Ravi P. Agarwal, Department of Mathematics, Texas A & M, University-Kingsville, 700 University Blvd., MSC 172, Kingsville, TX 78363-8202, USA.

Email: [email protected]

Search for more papers by this author

First published: 28 September 2021

https://doi.org/10.1002/cmm4.1195

Citations: 2

Share a link

Email
Wechat
Bluesky

Abstract

In this work, we focus on the non-linear fourth order class of singular boundary value problem which contains the parameter $λ$ . We convert this non-linear differential equation into third order non-linear differential equation. The third order problem is singular, non self adjoint, and nonlinear. Moreover, depending upon $λ$ , it admits multiple solutions. Hence, it is too difficult to capture these solutions by any discrete method such as finite difference and so forth. Here we develop an iterative technique with the help of homotopy perturbation method and variational iteration method in a suitable way. Convergence of this series solution is studied in a novel way. We compute these solutions numerically. For small positive values of $λ$ , singular BVP has two solutions while solutions can not be found for large positive values of $λ$ . Furthermore, we also find dual solutions for $λ < 0$ .

1 INTRODUCTION

Molecular beam epitaxy is a technique of depositing epitaxial thin films^{1, 2} from molecular or atomic beams on a heated crystaline substrate under ultra-high vacuum (UHV) conditions. It has a lot of advantages over other epitaxial techniques such as LPE, HVPE, and so forth. A particular advantage is that it permits the growth of crystalline layers at desire temperatures where solid-state diffusion is negligible. In Reference 3, Escudero et al. consider the function

φ : Ω \subset ℝ^{2} \times ℝ^{+} \to ℝ,

()

which describes the height of growing interface at a spatial point

x \in Ω \subset ℝ^{2}

at time

t \in ℝ^{+}

. They considered conservative counterpart of the Kardar–Parisi–Zhang equation⁴

φ_{t} = - μ Δ^{2} φ + ζ Δ {|\nabla φ|}^{2} + η (x, t),

()

where

x = (x_{1}, x_{2})

be the spatial variable and

η (x, t)

be the noise term or viscosity term such that Gaussian distributed random variable⁵ takes the account of the thermal fluctuations. After simplification as given in Reference 3, from (2) we get

φ_{t} = 2 K_{1} \det (D^{2} φ) - K_{2} \nabla^{4} φ + η (x, t) .

()

The Equation (3) is known as a higher order conservative counterpart of the Kardar–Parisi–Zhang equation,⁴ which is an analogue of Equation (2). It is conservative in the sense that, if we choose appropriate boundary condition, then we get the first moment

\int_{Ω} σ d x

as a constant. Each terms in Equation (3) have a clear geometrical meaning which was described in Reference 3. To know more about

η (x, t)

, reader may read Reference 5. Now, we set Equation (3) in a possible continuum description.⁶ Therefore the stationary version of (3) is given by

\begin{align} Δ^{2} φ = \det (D^{2} φ) + λ f (x), x \in ℝ^{2}, \\ boundary conditions, \end{align}

()

where

λ

is a parameter and

f (x)

is a know function. In the following, we consider homogeneous Dirichlet and Navier boundary conditions, which are

φ = 0, \frac{\partial φ}{\partial n} = 0 on \partial Ω .

()

and

φ = 0, Δ φ = 0 on \partial Ω,

()

where n is unit normal to

\partial Ω

, respectively. In Reference 7, Escudero et al. theoretically proved that, for any

f (x) \in L^{1} (Ω)

\exists λ_{0} \in ℝ

such that

0 < λ < λ_{0}

the problem (4) has at least two solutions. Now we set the problem on a unit disk and consider

f (x) = 1 .

Define

r = | x |, φ (x) = ϕ (| x |) .

()

Using (7) and (4), we get a fourth order singular non-self adjoint⁸^{(p. 58)} boundary value problem

\frac{1}{r} {[r {\{\frac{1}{r} {(r ϕ^{'})}^{'}\}}^{'}]}^{'} = \frac{ϕ^{'} ϕ^{''}}{r} + λ .

()

Subject to homogeneous Dirichlet boundary condition is

ϕ^{'} (0) = 0, ϕ (1) = 0, ϕ^{'} (1) = 0, \lim_{r \to 0} r ϕ^{'''} (r) = 0,

()

and homogeneous Navier boundary condition of type one is

ϕ^{'} (0) = 0, ϕ (1) = 0, ϕ^{'} (1) + ϕ^{''} (1) = 0, \lim_{r \to 0} r ϕ^{'''} (r) = 0,

()

and homogeneous Navier boundary condition of type two is

ϕ^{'} (0) = 0, ϕ (1) = 0, ϕ^{''} (1) = 0, \lim_{r \to 0} r ϕ^{'''} (r) = 0 .

()

In Reference 3 Escudero et al. proved that, there exists

λ_{0} \in ℝ

such that

0 < λ < λ_{0}

the Equation (8) has at least two solutions. They did not find the value of

λ_{0}

. By using the variational approach, they proved that for

0 \leq λ < λ_{0}

the Equation (8) has two solutions. Corresponding to Dirichlet boundary condition, the estimated value of

λ_{0}

is between 144 and 307 and corresponding to Equation (11), the estimated value of

λ_{0}

is lie in the interval

9 \leq λ_{0} \leq 11.63

.⁹ They did not give any conclusion regarding Equation (10) and

λ < 0

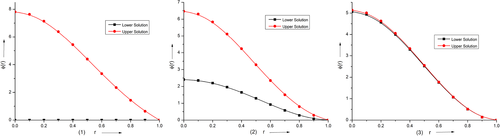
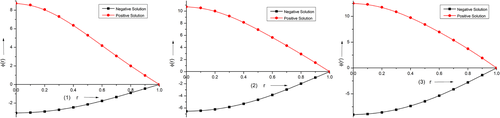
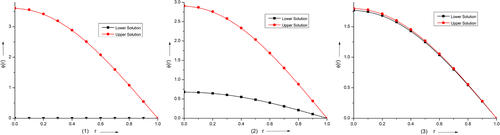
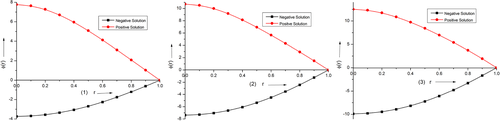
In 2019, Verma et al. extend their results analytically as well as numerically. By using monotone upper and lower solution technique, they¹⁰ established the existence of the solution and derived the rigorous bounds of the parameter corresponding to the boundary conditions (9) to (11). They also applied^{11, 12} HPM, VIM, and Adomian decomposition method on the second order SBVP which arise in the MBE. In Reference 13, they have applied Adomian decomposition method on fourth order singular boundary value problem. Recently, they¹⁴ have proposed system of fourth order singular boundary value problem based on Equation (8). To the best of our knowledge, there is no other work related to the governing problem in the literature.

Furthermore, we have noticed few gaps related to the problem (8). The problem (8) is non self adjoint, singularity present at the origin, non linear and included a parameter $λ$ . Again, it always occurred two solution for prescribed value of $λ$ . Therefore, it is difficult to predict the both solutions by using discrete method based on collocation points.

Motivated by the above literature, we propose an iterative technique by using HPM and VIM¹⁵ and apply to the third order SBVP directly. We establish the convergence analysis of our propose method. Many authors have applied HPM method to find numerical or analytical solution on fourth order singular differential equation^{16, 17} as well as sixth order differential equation.¹⁸ Recently, Bota and Cruntu¹⁹ applied this technique to find the analytical solution of nonlinear differential equation. The convergence of the method was established by Ayati and Biazar in Reference 20. He et al.²¹ applied HPM to third order Duffing equation and time-fractional frequency-amplitude formulation for nonlinear oscillators. The basic introduction about variational principle can be found in References 22-24. To know more about this method and its convergence reader can read the reference and the references therein.²⁵ The advantage of our proposed technique is to capture dual solutions with high accuracy.

This article is structured in seven sections. Sections 2 is dedicated to the description of the numerical methods. In Section 3, we sketch the details of the computations for the proposed technique. Convergence analysis is given in Section 4. Computed results are presented in Section 5. Finally, our conclusion is discussed in Section 6.

2 DESCRIPTION OF THE ITERATIVE METHODS

Here we describe about the methods. To know more about these two methods reader may read the corresponding references.

2.1 HPM

HPM proposed by He.¹⁷ He applied this technique to nonlinear singular boundary value problem.^{26, 27} Here, to demonstrate the methodology, we consider the following nonlinear problem

L (y) + N (y) = λ g (r), r \in [0, 1],

()

where L is the linear differential operator, N is the nonlinear operator, and

g (r)

is the source term with

λ

as a parameter. We construct the homotopy¹⁵

v (r, q) : [0, 1] \times [0, 1] \to ℝ

, which satisfies

H (y, r, q) = (1 - q) [L (y) - L (u_{0})] + q [L (y) + N (y) - λ g (r)] = 0, q \in [0, 1], r \in [0, 1],

()

where

q \in [0, 1]

is the perturbation parameter and

u_{0}

is an initial guess. We choose

u_{0}

in such a way so that it satisfies both linear operator and initial condition. Therefore from (13), we have

\begin{align} q = 0 : H (y, r, 0) = L (y) - L (u_{0}) = 0, \end{align}

()

\begin{align} q = 1 : H (y, r, 1) = L (y) + N (y) - λ g (r) = 0 . \end{align}

()

Now, we decompose the solution in a power series expression, which is

y (r, q) = y_{0} + q y_{1} + q^{2} y_{2} + \dots

()

Here

y_{i}

i = 0, 1, 2, \dots

are unknown functions which are to be determined. We approximate the nonlinear term in terms of He's polynomial which is given by

N (y (r)) = N (\sum_{j = 0}^{\infty} y_{j} (r)) = \sum_{i = 0}^{\infty} H_{i} (y_{0}, y_{1}, \dots, y_{i}),

()

where,

H_{i} = \frac{1}{i!} \frac{d^{i}}{d β^{i}} N {(\sum_{j = 0}^{i} β^{j} y_{j})}_{β = 0}, i = 0, 1, 2, \dots

()

Substituting all the values of (17) and (16) in (13), we have

\begin{align} q^{0} : L (y_{0}) - L (u_{0}) = 0, \end{align}

()

\begin{align} q^{1} : L (y_{1}) + L (u_{0}) + H_{0} - λ g (r) = 0, \end{align}

()

\begin{align} ⋮ \end{align}

\begin{align} q^{n + 1} : L (y_{n + 1}) + H_{n} = 0, \end{align}

()

\begin{align} ⋮, \end{align}

and so on. The approximate solution of Equation (12) is

y (r) = \sum_{i = 0}^{\infty} y_{i}

2.2 VIM

He²⁸ proposed the VIM method to approximate the solution of some well known nonlinear problems. In view of Reference 28, we can write the correctional functional of VIM corresponding to Equation (12) in the following form

\begin{align} y_{n + 1} (r) = y_{n} (r) + \int_{0}^{r} η (t) (L y_{n} (t) + N {\tilde{y}}_{n} (t) - λ g (t)) d t, \end{align}

()

where

η (t)

is the Lagrange multiplier and

{\tilde{y}}_{n}

is of restricted variation that is,

δ {\tilde{y}}_{n} = 0

.¹⁵ We can determine the optimal value of

η (t)

by using variational principle. The exact solution

y (r)

of Equation (12) is given by

y (r) = \lim_{n \to \infty} y_{n} (r) .

3 DERIVATION OF THE PROPOSED METHOD

Here, we apply our proposed method which is based on HPM and VIM on third order SBVP. We may call this propose method as HPM coupled with VIM method. We can write the Equation (8) in the following form

r^{3} ϕ^{(i v)} + 2 r^{2} ϕ^{'''} - r ϕ^{''} + ϕ^{'} = r^{2} ϕ^{'} ϕ^{''} + λ r^{3} .

()

Equivalently, we have

\begin{align} ϕ^{'} = y, \end{align}

()

\begin{align} and r^{3} y^{'''} + 2 r^{2} y^{''} - r y^{'} + y = r^{2} y y^{'} + λ r^{3} . \end{align}

()

Subject to the Dirichlet boundary condition is

ϕ (1) = 0, y (0) = 0, y (1) = 0, \lim_{r \to 0} r y^{''} (r) = 0,

()

Navier boundary condition of type one is

ϕ (1) = 0, y (0) = 0, y (1) + y^{'} (1) = 0, \lim_{r \to 0} r y^{''} (r) = 0,

()

and Navier boundary condition of type two is

ϕ (1) = 0, y (0) = 0, y^{'} (1) = 0, \lim_{r \to 0} r y^{''} (r) = 0 .

()

We can easily show that Equation (25) is non-self adjoint.⁸^{(p. 58)} From (25), we have

L (y) = r^{3} y^{'''} + 2 r^{2} y^{''} - r y^{'} + y, N (y) = - r^{2} y y^{'} and g (r) = λ r^{3} .

()

Now from (19)–(21), we get

\begin{align} q^{0} : L (y_{0}) - L (u_{0}) = 0, \end{align}

()

\begin{align} q^{1} : L (y_{1}) + L (u_{0}) - r^{2} y_{0} y_{0}^{'} - λ r^{3} = 0, \end{align}

()

\begin{align} q^{2} : L (y_{2}) + H_{1} = 0, \end{align}

()

\begin{align} ⋮ \end{align}

\begin{align} q^{n + 1} : L (y_{n + 1}) + H_{n} = 0, \end{align}

()

\begin{align} ⋮, \end{align}

and so on. By using (29), we have

N (\sum_{j = 0}^{\infty} y_{j} (r)) = - r^{2} (\sum_{j = 0}^{\infty} y_{j} (r)) (\sum_{j = 0}^{\infty} y_{j}^{'} (r)) = \sum_{i = 0}^{\infty} H_{i} (y_{0}, y_{1}, \dots, y_{i}),

()

where

H_{i}

can be written as

H_{i} (y_{0}, y_{1}, \dots, y_{i}) = - r^{2} \sum_{j = 0}^{i} y_{i - j} (r) y_{j}^{'} (r) .

()

We consider

y_{0} (r) = a r

and

u_{0} (r) = a r

. To solve Equations (31)–(33), we use VIM. Set

y_{1} (r) = v (r)

. Now, the variational correctional formula of (31) can be written as

v_{n + 1} (r) = v_{n} (r) + \int_{0}^{r} η (t) (t^{3} v_{n}^{'''} (t) + 2 t^{2} v_{n}^{''} (t) - t v_{n}^{'} (t) + v_{n} (t) + H_{0} (y_{0} (t)) - λ t^{3}) d t,

()

where

η (t)

be the Lagrange multiplier. Now, we operate variation

δ

on (36) from both sides. Hence, we have,

δ v_{n + 1} (r) = δ v_{n} (r) + δ \int_{0}^{r} η (t) (t^{3} v_{n}^{'''} (t) + 2 t^{2} v_{n}^{''} (t) - t v_{n}^{'} (t) + v_{n} (t) + H_{0} (y_{0} (t)) - λ t^{3}) d t .

()

After simplification as in Reference 15, we have the optimal value of

η (t)

, which is given by

η (t) = (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) .

()

Therefore from (36), we have

v_{n + 1} = v_{n} + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (t^{3} v_{n}^{'''} + 2 t^{2} v_{n}^{''} - t v_{n}^{'} + v_{n} + H_{0} (y_{0}) - λ t^{3}) d t .

()

We choose

v_{0} (r) = 0

and consider

y_{1} (r) = v (r) = v_{1} (r)

. Therefore, the Equation (31) becomes

y_{1} (r) = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{0} (y_{0} (t)) - λ t^{3}) d t .

()

By similar analysis, we have

\begin{align} y_{2} (r) = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{1} (y_{0} (t), y_{1} (t))) d t, \end{align}

()

\begin{align} y_{3} (r) = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{2} (y_{0} (t), y_{1} (t), y_{2} (t))) d t, \end{align}

()

\begin{align} ⋮ \end{align}

\begin{align} y_{n + 1} (r) = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{n} (y_{0} (t), \dots, y_{n} (t))) d t, \end{align}

()

\begin{align} ⋮, \end{align}

and so on. The approximate solution

y (r)

y (r) = \sum_{i = 0}^{\infty} y_{i} (r)

. Now we will show that the series

\sum_{i = 0}^{\infty} y_{i} (r)

is convergent and converge to the exact solution

y (r)

4 CONVERGENCE ANALYSIS

Let ${S_{n}}$ be the sequence of nth partial sum of the series solution $\sum_{i = 0}^{\infty} y_{i}$ . Then the solution $y (r)$ is given by $y (r) = \lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \sum_{i = 0}^{n} y_{i}$ . Now, we prove the series solution $\sum_{i = 0}^{\infty} y_{i} (r)$ is convergent.

We construct the series of the form

S_{0} + (S_{1} - S_{0}) + (S_{2} - S_{1}) + \dots + (S_{n} - S_{n - 1}) + \dots = S_{0} + \sum_{i = 0}^{\infty} (S_{i + 1} - S_{i}) .

()

For every sequence

S_{n} = \sum_{i = 0}^{n} y_{i} (r)

, we approximate

N (\sum_{i = 0}^{n} y_{i} (r))

^{29, 30} by

N (\sum_{i = 0}^{n} y_{i} (r)) = - r^{2} (\sum_{i = 0}^{n} y_{i} (r)) {(\sum_{i = 0}^{n} y_{i} (r))}^{'} = \sum_{i = 0}^{n} H_{i} (y_{0}, y_{1}, \dots, y_{i}) .

()

Equivalently, we have

N (S_{n}) = - r^{2} (S_{n}) {(S_{n})}^{'} = \sum_{i = 0}^{n} H_{i} (y_{0}, y_{1}, \dots, y_{i}) .

()

Lemma 1.Let $y_{0} (r) = a r, a \in ℝ$ be the initial approximation and $y_{n} \in C^{3} (0, 1], \forall n \in ℕ$ . Then $y_{n} (0) = 0$ , $y_{n}^{'} (r), y_{n}^{''} (r), y_{n}^{'''} (r), y_{n}^{(i v)} (r), \frac{H_{n}}{r^{3}}$ are bounded on $[0, 1]$ and $y_{n} \in C^{3} [0, 1]$ for all $n \in ℕ$ .

Proof.From (35), we have

\lim_{r \to 0} \frac{H_{0}}{r^{3}} = \lim_{r \to 0} \frac{- r^{2} y_{0} y_{0}^{'}}{r^{3}} = \lim_{r \to 0} \frac{- y_{0} y_{0}^{''} - y_{0}^{'} y_{0}^{'}}{1} = - a^{2} .

()

So,

\frac{H_{0}}{r^{3}}

is bounded on

[0, 1]

. From Equation (40), we get

\begin{align} y_{1}^{'} (r) = \int_{0}^{r} (\frac{t \log (t)}{2} - \frac{t (2 \log (r) + 1)}{4} + \frac{t^{3}}{4 r^{2}}) (\frac{H_{0} (y_{0} (t))}{t^{3}} - λ) d t, \end{align}

()

\begin{align} y_{1}^{''} (r) = \int_{0}^{r} (- \frac{t}{2 r} - \frac{t^{3}}{2 r^{3}}) (\frac{H_{0} (y_{0} (t))}{t^{3}} - λ) d t, \end{align}

()

\begin{align} y_{1}^{'''} (r) = \int_{0}^{r} (\frac{t}{2 r^{2}} + \frac{3 t^{3}}{2 r^{4}}) (\frac{H_{0} (y_{0} (t))}{t^{3}} - λ) d t, \end{align}

()

\begin{align} y_{1}^{(i v)} (r) = \int_{0}^{r} (\frac{- t}{r^{3}} - \frac{6 t^{3}}{r^{5}}) (\frac{H_{0} (y_{0} (t))}{t^{3}} - λ) d t . \end{align}

()

Since

0 \leq t \leq r \leq 1

, and

y_{n} \in C^{3} (0, 1]

, then by second fundamental theorem of calculus,³¹^{(theorem.34.3, p. 294)} we conclude that

y_{1} (0) = 0

y_{1}^{'} (r)

y_{1}^{''} (r)

y_{1}^{'''} (r)

y_{1}^{(i v)} (r)

are bounded on

[0, 1]

and

y_{1} \in C^{3} [0, 1]

. Again,

\lim_{r \to 0} \frac{H_{1}}{r^{3}} = \lim_{r \to 0} \frac{- r^{2} y_{0} y_{1}^{'} - r^{2} y_{1} y_{0}^{'}}{r^{3}} = \lim_{r \to 0} \frac{- y_{0} y_{1}^{''} - 2 y_{0}^{'} y_{1}^{'} - y_{0}^{''} y_{1}}{1} .

()

Therefore,

\frac{H_{1}}{r^{3}}

is bounded on

[0, 1]

. Hence, our assumptions are true for the induction parameter

n = 1

. Let our assumptions be true upto

n = m

. Hence,

y_{n} (0) = 0, y_{n}^{'} (r), y_{n}^{''} (r), y_{n}^{'''} (r), y_{n}^{(i v)} (r) and \frac{H_{n}}{r^{3}} are bounded on [0, 1] for all n = 1, 2, \dots, m .

()

Let

y_{m} \in C^{3} [0, 1] for all n = 1, 2, \dots, m .

Now, for

n = m + 1

, we have

\begin{align} y_{m + 1}^{'} (r) = \int_{0}^{r} (\frac{t \log (t)}{2} - \frac{t (2 \log (r) + 1)}{4} + \frac{t^{3}}{4 r^{2}}) (\frac{H_{m} (y_{0} (t), \dots, y_{m})}{t^{3}}) d t, \end{align}

()

\begin{align} y_{m + 1}^{''} (r) = \int_{0}^{r} (- \frac{t}{2 r} - \frac{t^{3}}{2 r^{3}}) (\frac{H_{m} (y_{0} (t), \dots, y_{m} (t))}{t^{3}}) d t, \end{align}

()

\begin{align} y_{m + 1}^{'''} (r) = \int_{0}^{r} (\frac{t}{2 r^{2}} + \frac{3 t^{3}}{2 r^{4}}) (\frac{H_{m} (y_{0} (t), \dots, y_{m} (t))}{t^{3}}) d t, \end{align}

()

\begin{align} y_{m + 1}^{(i v)} (r) = \int_{0}^{r} (\frac{- t}{r^{3}} - \frac{6 t^{3}}{r^{5}}) (\frac{H_{m} (y_{0} (t), \dots, y_{m} (t))}{t^{3}}) d t . \end{align}

()

Similarly, since

0 \leq t \leq r \leq 1

and

y_{m} \in C^{3} [0, 1] for all n = 1, 2, \dots, m .

, then we conclude that

y_{m + 1} (0) = 0

y_{m + 1}^{'} (r)

y_{m + 1}^{''} (r)

y_{m + 1}^{'''} (r)

y_{m + 1}^{(i v)} (r)

are bounded on

[0, 1]

and

y_{m + 1} \in C^{3} [0, 1]

. Again from (35), we have

\lim_{r \to 0} \frac{H_{m + 1}}{r^{3}} = \lim_{r \to 0} \frac{- r^{2} \sum_{i = 0}^{m + 1} y_{\overline{(m + 1) - i}} y_{i}^{'}}{r^{3}} = \lim_{r \to 0} \frac{- \sum_{i = 0}^{m + 1} (y_{\overline{(m + 1) - i}} y_{i}^{''} + y_{\overline{(m + 1) - i}}^{'} y_{i}^{'})}{1} .

()

So,

\frac{H_{m + 1}}{r^{3}}

is also bounded on

[0, 1]

. Hence by mathematical induction, we have

y_{n} (0) = 0, y_{n}^{'} (r), y_{n}^{''} (r), y_{n}^{'''} (r), y_{n}^{(i v)} (r), \frac{H_{n}}{r^{3}} are bounded on [0, 1] and y_{n} \in C^{3} [0, 1] for all n = 1, 2, \dots

()

This completes the proof.

Corollary 1.Let $y_{n} (r) \in C^{3} [0, 1]$ for all $n \in ℕ \cup {0}$ . Then

a) $S_{n}^{'} (r)$ is bounded on $[0, 1]$ for $n \geq 0$ .

b) $S_{n} (0) - S_{n - 1} (0) = 0$ for each $n \in ℕ$ .

Proof.a) From definition of $S_{n}$ , we have

\begin{align} S_{0} (r) = y_{0} (r), \end{align}

()

\begin{align} S_{1} (r) = y_{0} (r) + y_{1} (r), \end{align}

()

\begin{align} ⋮ \\ S_{n} (r) = y_{0} (r) + y_{1} (r) + \dots + y_{n} (r), \end{align}

()

\begin{align} ⋮, \end{align}

and so on. By using Lemma 1, we can easily conclude that

S_{n}^{'} (r)

is bounded for all

n \in ℕ \cup {0}

b) Again by using Lemma 1, we have $S_{n} (0) - S_{n - 1} (0) = y_{0} (0) + y_{1} (0) + \dots + y_{n} (0) - y_{0} (0) - y_{1} (0) - \dots - y_{n - 1} (0) = y_{n} (0) = 0$ for each $n \in ℕ$ .

Definition 1.Let $g (r), h (r) : [0, 1] \to ℝ$ be the functions. $g (r)$ is said to be big ohh of $h (r)$ if there exists a constant $M > 0$ such that,

|g (r)| \leq M |h (r)|, \forall r \in [0, 1],

()

and denoted by

g (r) = O (h (r))

.³²

Lemma 2.Let $y_{n} (r) \in C^{3} [0, 1]$ and $p_{n} = \sup_{r \in [0, 1]} | H_{n} |$ for all $n \in ℕ \cup {0}$ . If there exist $k_{0} \in ℕ$ such that $p_{i + 1} \leq p_{i}, \forall i \geq k_{0}$ , then there exists a real number $K_{1} > 0$ such that $|\frac{S_{n} (r) + S_{n - 1} (r)}{r}| \leq K_{1}, \forall r \in [0, 1]$ , $\forall n \in ℕ$ .

Proof.From definition of $S_{n}$ and for $n = 1$ , we have there exist a real number $k_{1} > 0$ that is,

|\frac{S_{1} + S_{0}}{r}| = |\frac{y_{1} + 2 y_{0}}{r}| \leq k_{1}, \forall r \in [0, 1] .

()

For

n = 2

, we have

|\frac{S_{2} + S_{1}}{r}| = |\frac{2 y_{1} + 2 y_{0} + y_{2}}{r}| \leq |\frac{y_{1} + 2 y_{0}}{r}| + |\frac{y_{1} + y_{2}}{r}| \leq k_{1} + |\frac{y_{1} + y_{2}}{r}|, \forall r \in [0, 1] .

()

By using Lemma 1, we can show that

|\frac{y_{1} + y_{2}}{r}|

is bounded on

[0, 1]

. Take

k_{2} = k_{1} + \sup_{r \in [0, 1]} |\frac{y_{1} + y_{2}}{r}| .

For

n = 3

, we have

\begin{align} |\frac{S_{3} + S_{2}}{r}| & = |\frac{2 y_{1} + 2 y_{0} + 2 y_{2} + y_{3}}{r}|, \\ \leq |\frac{2 y_{1} + 2 y_{0} + y_{2}}{r}| + |\frac{y_{2} + y_{3}}{r}|, \\ \leq k_{2} + |\frac{y_{2} + y_{3}}{r}|, \forall r \in [0, 1] . \end{align}

()

Again, we take

k_{3} = k_{2} + \sup_{r \in [0, 1]} |\frac{y_{2} + y_{3}}{r}| .

In general, we have

|\frac{S_{m} + S_{m - 1}}{r}| \leq |\frac{2 y_{1} + 2 y_{0} + \dots + y_{m - 1}}{r}| + |\frac{y_{m - 1} + y_{m}}{r}| \leq k_{m - 1} + |\frac{y_{m - 1} + y_{m}}{r}|, \forall r \in [0, 1] .

()

Similarly, we have

k_{m} = k_{m - 1} + \sup_{r \in [0, 1]} |\frac{y_{m - 1} + y_{m}}{r}| .

For

n = m + 1

, we have

|\frac{S_{m + 1} + S_{m}}{r}| \leq |\frac{2 y_{1} + 2 y_{0} + \dots + y_{m}}{r}| + |\frac{y_{m} + y_{m + 1}}{r}| \leq k_{m} + |\frac{y_{m} + y_{m + 1}}{r}|, \forall r \in [0, 1] .

()

and take

k_{m + 1} = k_{m} + \sup_{r \in [0, 1]} |\frac{y_{m} + y_{m + 1}}{r}| .

Finally, we get

|\frac{S_{n} + S_{n - 1}}{r}| \leq k_{n}, \forall r \in [0, 1], where k_{n} = k_{n - 1} + \sup_{r \in [0, 1]} |\frac{y_{n - 1} + y_{n}}{r}|, \forall n \in ℕ .

()

Hence, we have there exists a natural number m that is,

|k_{n} - k_{n - 1}| = \sup_{r \in [0, 1]} |\frac{y_{n - 1} + y_{n}}{r}|, \forall n \geq m .

()

Now, we want to show that the sequence

{k_{n}}

defined by (70) is eventually constant sequence. Now,

y_{0} = a r, y_{0}^{'} = a .

()

Therefore, from the definition of big ohh, we can write

y_{0} = O (r)

and

y_{0}^{'} = O (1)

. Now, we have

H_{n} (y_{0}, \dots, y_{n}) = - r^{2} \sum_{i = 0}^{n} y_{n - i} y_{i}^{'} .

()

Therefore for

n = 0

, from (72), we get

H_{0} (y_{0}) = - r^{2} y_{0} y_{0}^{'} \Rightarrow H_{0} (y_{0}) = O (r^{3})

. Now from (40) and (48), we have

\begin{align} |y_{1}| \leq \int_{0}^{r} r^{2} |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) - 1)}{4 r} - \frac{t^{3}}{4 r^{3}}| |\frac{H_{0} (y_{0} (t))}{t^{3}} - λ| d t, \end{align}

()

\begin{align} |y_{1}^{'}| \leq \int_{0}^{r} r |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) + 1)}{4 r} + \frac{t^{3}}{4 r^{3}}| |\frac{H_{0} (y_{0} (t)}{t^{3}}) - λ| d t . \end{align}

()

Since

0 \leq t \leq r

, by using Lemma 1, we can take

l_{0} = \sup_{r \in [0, 1]} \{|\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) - 1)}{4 r} - \frac{t^{3}}{4 r^{3}}| |\frac{H_{0} (y_{0} (t))}{t^{3}} - λ|\}

and

l_{1} = \sup_{r \in [0, 1]} \{|\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) + 1)}{4 r} + \frac{t^{3}}{4 r^{3}}| |\frac{H_{0} (y_{0} (t)}{t^{3}}) - λ|\}

. So, we have

y_{1} = O (r^{3})

and

y_{1}^{'} = O (r^{2})

. Again from Equation (72), we get

H_{1} (y_{0}, y_{1}) = - r^{2} \sum_{i = 0}^{1} y_{1 - i} y_{i}

. Therefore,

H_{1} (y_{0}, y_{1}) = - r^{2} y_{1} (r) y_{0}^{'} (r) - r^{2} y_{0} (r) y_{1}^{'} (r)

. Therefore by using the properties of big ohh, we have

H_{1} (y_{0}, y_{1}) = O (r^{5})

. Let our assumptions be true upto

n = m

. Hence, we have

\begin{align} y_{0} = O (r), y_{1} = O (r^{3}), \dots, y_{m} = O (r^{2 m + 1}), \end{align}

()

\begin{align} y_{0}^{'} = O (1), y_{1}^{'} = O (r^{2}), \dots, y_{m}^{'} = O (r^{2 m}), \end{align}

()

\begin{align} H_{0} (y_{0}) = O (r^{3}), H_{1} (y_{0}, y_{1}) = O (r^{5}), \dots, H_{m} (y_{0}, \dots, y_{m}) = O (r^{2 m + 3}) . \end{align}

()

Now, for

n = m + 1

, we have

\begin{align} |y_{m + 1}| & \leq \int_{0}^{r} r^{2} |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) - 1)}{4 r} - \frac{t^{3}}{4 r^{3}}| |\frac{H_{m} (y_{0} (t), \dots, y_{m} (t))}{t^{3}}| d t, \end{align}

()

\begin{align} \leq \int_{0}^{r} r^{2} |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) - 1)}{4 r} - \frac{t^{3}}{4 r^{3}}| p_{m} t^{2 m} d t, p_{m} is a fixed constant. \end{align}

()

Hence, we conclude that

y_{m + 1} = O (r^{2 m + 3})

. Now,

|y_{m + 1}^{'}| \leq \int_{0}^{r} r |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) + 1)}{4 r} + \frac{t^{3}}{4 r^{3}}| |\frac{H_{m} (y_{0} (t), \dots, y_{m} (t))}{t^{3}}| d t .

()

By similar analysis, we have

y_{m + 1}^{'} = O (r^{2 m + 2})

. Again, we have

H_{m + 1} (y_{0}, \dots, y_{m + 1}) = - r^{2} \sum_{i = 0}^{m + 1} y_{\overline{(m + 1) - i}} y_{i}^{'}

. Therefore, we get

H_{m + 1} (y_{0}, \dots, y_{m + 1}) = y_{m + 1} y_{0}^{'} + \dots + y_{0} y_{m + 1}^{'} \Rightarrow H_{m + 1} (y_{0}, \dots, y_{m + 1}) = O (r^{2 m + 5})

. Hence, by mathematical induction, we conclude that

y_{n + 1} = O (r^{2 n + 3}), y_{n + 1}^{'} = O (r^{2 n + 2}) and H_{n + 1} (y_{0}, \dots, y_{n + 1}) = O (r^{2 n + 5}) for all n \in ℕ \cup {0} .

()

Now,

\begin{align} |\frac{y_{n + 1} + y_{n}}{r}| & \leq \int_{0}^{r} r |\frac{t \log (t)}{2 r} - \frac{t (2 \log (r) - 1)}{4 r} - \frac{t^{3}}{4 r^{3}}| |\frac{H_{n}}{t^{3}} + \frac{H_{n - 1}}{t^{3}}| d t, \end{align}

()

\begin{align} \leq \int_{0}^{r} r l_{0} (p_{n} t^{2 n + 3} + p_{n - 1} t^{2 n + 1}) d t, p_{n}, p_{n - 1} > 0 are fixed constants, \end{align}

()

\begin{align} \leq \frac{l_{0} p_{n} r^{2 n + 5}}{(2 n + 4)} + \frac{l_{0} p_{n - 1} r^{2 n + 3}}{(2 n + 2)} . \end{align}

()

Therefore, we have

\begin{align} \sup_{r \in [0, 1]} |\frac{y_{n + 1} + y_{n}}{r}| \leq \frac{l_{0} p_{n}}{(2 n + 4)} + \frac{l_{0} p_{n - 1}}{(2 n + 2)} . \end{align}

()

\begin{align} Taking limit from both sides, \lim_{n \to \infty} \sup_{r \in [0, 1]} |\frac{y_{n + 1} + y_{n}}{r}| \leq \lim_{n \to \infty} (\frac{l_{0} p_{n}}{(2 n + 4)} + \frac{l_{0} p_{n - 1}}{(2 n + 2)}) . \end{align}

()

Since

p_{n + 1} \leq p_{n}

, hence by sandwich theorem, we have

\lim_{n \to \infty} \sup_{r \in [0, 1]} |\frac{y_{n + 1} + y_{n}}{r}| = 0 .

()

Therefore, from (70) and (87), we get there exist a natural number m such that

k_{n} = k_{n - 1}, \forall n \geq m,

()

where each

k_{i}, i = 0, 1, 2, \dots

are fixed real constants. Hence, the sequence

{k_{n}}

is an eventually constant sequence. Therefore, it is bounded. This completes the proof.

Lemma 3.Let ${S_{n}}$ be the sequence of nth partial sum of the series defined by (44). Then the sequence ${S_{n}}$ can be written as follows:

S_{n} = C + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) {N (S_{n - 1})} d t, n \geq 1,

()

where

C = a r + \frac{λ r^{3}}{16}

and N is the nonlinear operator defined by (45).

Proof.By using Equations (41)–(43), we get

\begin{align} S_{n} (r) \end{align}

\begin{align} = y_{0} + y_{1} + \dots + y_{n}, \end{align}

()

\begin{align} = a r + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{1} (y_{0} (t), y_{1} (t))) d t + \dots \end{align}

\begin{align} \dots + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (H_{n - 1} (y_{0} (t), \dots, y_{n} (t))) d t, \end{align}

()

\begin{align} = a r + \frac{λ r^{3}}{16} + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) \sum_{i = 0}^{n - 1} (H_{n - 1} (y_{0} (t), \dots, y_{n} (t))) d t, \end{align}

()

\begin{align} = C + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) N (\sum_{i = 0}^{n - 1} y_{i}) d t, (Using (45)). \end{align}

()

This completes the proof.

Theorem 1.Let $y_{0} (r) = a r$ and $y_{n} \in C^{3} [0, 1], \forall n \in ℕ$ . Then $\sum_{i = 0}^{\infty} y_{i}$ will converge uniformly to the exact solution $y (r)$ of Equation (25) for $r \in [0, 1]$ .

Proof.By using Lemma 3 and Equation (89), for $n = 1$ we have

\begin{align} S_{1} & = C + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) {N (S_{0})} d t, \end{align}

()

\begin{align} = S_{0} + \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (- t^{2} S_{0} S_{0}^{'} - λ t^{3}) d t, \end{align}

()

\begin{align} = S_{0} + \int_{0}^{r} (\frac{t r \log (t)}{2} - \frac{t r (2 \log (r) - 1)}{4} - \frac{t^{3}}{4 r}) (- \frac{S_{0} + S_{0}^{'}}{t} - λ) d t . \end{align}

()

Therefore, we have

|S_{1} - S_{0}| \leq \int_{0}^{r} ‖(\frac{t r \log (t)}{2} - \frac{t r (2 \log (r) - 1)}{4} - \frac{t^{3}}{4 r})‖ ‖(\frac{S_{0} + S_{0}^{'}}{t} + λ)‖ d t .

()

Let

K_{2} = \sup_{0 \leq t \leq r \leq 1} \{‖(\frac{t r \log (t)}{2} - \frac{t r (2 \log (r) - 1)}{4} - \frac{t^{3}}{4 r})‖ ‖(- \frac{S_{0} + S_{0}^{'}}{t} + λ)‖\}

and

K = \max {K_{1}, K_{2}, \frac{1}{2}}

, where

K_{1}

is defined by Lemma 2.

Therefore from (97), we get

|S_{1} - S_{0}| \leq \int_{0}^{r} K_{2} d z \leq \int_{0}^{r} K d t \leq K r .

()

Again, for $n = 2$ we have

\begin{align} (S_{2} - S_{1}) \end{align}

\begin{align} = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (N (S_{1}) - N (S_{0})) d t, \end{align}

()

\begin{align} = \int_{0}^{r} (\frac{r \log (t)}{2} - \frac{r (2 \log (r) - 1)}{4} - \frac{t^{2}}{4 r}) (S_{1} S_{1}^{'} - S_{0} S_{0}^{'}) d t, \end{align}

()

\begin{align} = {|(\frac{r \log (t)}{2} - \frac{r (2 \log (r) - 1)}{4} - \frac{t^{2}}{4 r}) (\frac{S_{1}^{2} - S_{0}^{2}}{2})|}_{0}^{r} - \int_{0}^{r} (\frac{r}{2 t} - \frac{t}{2 r}) (\frac{S_{1}^{2} - S_{0}^{2}}{2}) d t, \end{align}

()

\begin{align} = - \int_{0}^{r} (\frac{r}{2 t} - \frac{t}{2 r}) (\frac{S_{1}^{2} - S_{0}^{2}}{2}) d t, \end{align}

()

\begin{align} (using Lemma 4.1) \\ = - \int_{0}^{r} (\frac{r}{2} - \frac{t^{2}}{2 r}) (\frac{S_{1} + S_{0}}{2 t}) (S_{1} - S_{0}) d t . \end{align}

()

Therefore,

\begin{align} |S_{2} - S_{1}| \\ \leq \int_{0}^{r} |\frac{r}{2} - \frac{t^{2}}{2 r}| |\frac{S_{1} + S_{0}}{2 t}| |S_{1} - S_{0}| d t . \end{align}

()

Furthermore, we take

K_{3} = \sup_{0 \leq t \leq r \leq 1} |\frac{r}{2} - \frac{t^{2}}{2 r}| = \frac{1}{2} .

()

Therefore,

\begin{align} |S_{2} - S_{1}| \\ \leq \int_{0}^{r} K \times K \times K t d t, (using Lemma 4.2) \end{align}

()

\begin{align} \leq \frac{K^{3} r^{2}}{1.2} . \end{align}

()

By similar analysis, we have

|S_{3} - S_{2}| \leq \frac{K^{5} r^{3}}{3!},

()

and

|S_{4} - S_{3}| \leq \frac{K^{7} r^{4}}{4!} .

()

In general, we have

|S_{n} - S_{n - 1}| \leq \frac{K^{2 n - 1} r^{n}}{n!} .

()

Now,

\begin{align} (S_{n + 1} - S_{n}) \\ = \int_{0}^{r} (\frac{r \log (t)}{2 t^{2}} - \frac{r (2 \log (r) - 1)}{4 t^{2}} - \frac{1}{4 r}) (N (S_{n}) - N (S_{n - 1})) d t, \end{align}

()

\begin{align} = \int_{0}^{r} (\frac{r \log (t)}{2} - \frac{r (2 \log (r) - 1)}{4} - \frac{t^{2}}{4 r}) (S_{n} S_{n}^{'} - S_{n - 1} S_{n - 1}^{'}) d t, \end{align}

()

\begin{align} = {|(\frac{r \log (t)}{2} - \frac{r (2 \log (r) - 1)}{4} - \frac{t^{2}}{4 r}) (\frac{S_{n}^{2} - S_{n - 1}^{2}}{2})|}_{0}^{r} - \int_{0}^{r} (\frac{r}{2 t} - \frac{t}{2 r}) (\frac{S_{n}^{2} - S_{n - 1}^{2}}{2}) d t, \end{align}

()

\begin{align} = - \int_{0}^{r} (\frac{r}{2 t} - \frac{t}{2 r}) (\frac{S_{n}^{2} - S_{n - 1}^{2}}{2}) d t, \end{align}

()

\begin{align} (using Lemma 4.1) \\ = - \int_{0}^{r} (\frac{r}{2} - \frac{t^{2}}{2 r}) (\frac{S_{n} + S_{n - 1}}{2 t}) (S_{n} - S_{n - 1}) d t . \end{align}

()

Therefore, we have

|S_{n} - S_{n - 1}| \leq \frac{K^{2 n + 1} r^{n + 1}}{(n + 1)!} .

()

Now, we consider

S_{0} + \sum_{n = 1}^{\infty} \frac{K^{2 n - 1} r^{n}}{n!} .

()

By using D'Alembert ratio test, we can easily conclude that the series (117) is convergent for all

r \in ℝ

. Hence, by Weierstrass's M test, we have the series

S_{0} + \sum_{i = 0}^{\infty} (S_{i + 1} - S_{i})

is uniformly convergent. Since

\sum_{i = 0}^{\infty} y_{i}

is uniformly convergent and each

y_{n} (r) \in C^{3} [0, 1]

, then the limit function

y (r)

is also in

C^{3} [0, 1]

. This completes the proof.

5 NUMERICAL OBSERVATION

In this section, we have placed numerical data corresponding to Equation (8). We also have verified our numerical observations with theoretical results, which was proven by Escudero et al.⁹ and Verma et al.¹⁰ Numerical data computed by the proposed technique is well matched with the numerical data which was placed in References 9-12.

Here, we define the maximum absolute residue error by

| | E | |_{\infty} = \max_{i = 0, 1, \dots, 9} |R (r_{i})|

, where

r_{i} = r_{0} + i h

r_{0} = 0

and

h = 0.1

. The residue function of Equation (8) is given by

R (r) = \frac{1}{r} {\{r {[\frac{1}{r} {(r ϕ^{'})}^{'}]}^{'}\}}^{'} - \frac{1}{r} ϕ^{'} ϕ^{''} - λ .

()

5.1 Dirichlet boundary condition

Here, we consider the fourth order SBVP (8) corresponding to Dirichlet boundary condition defined by (9). By using (40)–(43), we have

\begin{align} y_{0} (r) = a r, \end{align}

()

\begin{align} y_{1} (r) = \frac{1}{16} r^{3} (a^{2} + λ), \end{align}

()

\begin{align} y_{2} (r) = \frac{1}{384} a r^{5} (a^{2} + λ), \end{align}

()

\begin{align} y_{3} (r) = \frac{r^{7} (a^{2} + λ) (7 a^{2} + 3 λ)}{73728}, \end{align}

()

\begin{align} y_{4} (r) = \frac{a r^{9} (a^{2} + λ) (19 a^{2} + 15 λ)}{5898240}, \\ ⋮, \end{align}

()

and so on. The approximate numerical solution are given by

y (r) = \sum_{i = 0}^{N} y_{i} (r)

, where N is a natural number chosen to get suitable accuracy. We determine the constant value a by using the boundary condition

y (1) = 0

. Again, by using

ϕ^{'} = y

and boundary condition

ϕ (1) = 0

, we can have the numerical approximation

ϕ (r)

of (8). In the below we describe two cases:

Case (a): Here, we see that two numerical solutions exits for $λ = 0$ . One solution is trivial and other is non-trivial. Moreover, we also get non-trivial dual solutions for $0 < λ \leq λ_{0}$ . The value of $λ_{0}$ approximated to be 168.76. In Table 1 and Figure 1 we have placed maximum absolute residual error $| | E | |_{\infty}$ and graphs corresponding to lower and upper solution for some positive $λ$ .

TABLE 1. Approximate upper solution and lower solution maximum absolute residual error corresponding to some positive

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
0	$9.88 \times 1 0^{- 2}$	0	0
120	$2.78 \times 1 0^{- 2}$	120	$1.17 \times 1 0^{- 13}$
168.76	$5.73 \times 1 0^{- 10}$	168.76	$1.01 \times 1 0^{- 10}$

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Approximate solutions $ϕ (r)$ corresponding to $(1) λ = 0$ , $(2) λ = 120$ , $(3) λ = 168.76$

Case (b): For $λ < 0$ , we always get non-trivial dual solutions. One is called positive solution and other is called negative solution. We could not find any negative critical value $λ$ . We see that solutions are moved apart from each other for decreasing the negative value of the parameter. In Table 2 and Figure 2, we have presented the numerical data of approximate solutions.

TABLE 2. Approximate negative solution and positive solution maximum absolute residual error corresponding to some negative

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
$-$ 20	$1.30 \times 1 0^{- 15}$	$-$ 20	$1.09 \times 1 0^{- 1}$
$-$ 60	$1.37 \times 1 0^{- 14}$	$-$ 60	$1.31 \times 1 0^{- 1}$
$-$ 100	$2.39 \times 1 0^{- 14}$	$-$ 100	$1.52 \times 1 0^{- 1}$

5.2 Navier boundary condition of type one

In this case, we consider the boundary conditions (10). The approximate solutions are given by $y (r) = \sum_{i = 0}^{N} y_{i}$ , where the iterations $y_{i} (r)$ are same as in example 5.1 and N is the natural number can be chosen to get the better accuracy. Here, we also determine the value of the constant a by using the boundary conditions $y (1) + y^{'} (1) = 0$ . Same remarks can be made as in example 5.1, except the critical value of $λ$ . The critical value of $λ$ can be approximated to be 31.94. Corresponding to some $λ$ , we have listed the numerical data of the approximate solutions in Tables 3 and 4, Figures 3 and 4.

TABLE 3. Approximate lower solution and upper solution maximum absolute residual error corresponding to some positive

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
0	0	0	$7.95 \times 1 0^{- 13}$
20	$6.55 \times 1 0^{- 15}$	20	$2.55 \times 1 0^{- 13}$
31.94	$1.06 \times 1 0^{- 14}$	31.94	$5.15 \times 1 0^{- 14}$

TABLE 4. Approximate positive solution and negative solution maximum absolute residual error corresponding to some negative

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
$-$ 100	$4.94 \times 1 0^{- 4}$	$-$ 100	$5.32 \times 1 0^{- 15}$
$-$ 300	$2.15 \times 1 0^{- 3}$	$-$ 300	$7.10 \times 1 0^{- 14}$
$-$ 500	$3.43 \times 1 0^{- 3}$	$-$ 500	$3.19 \times 1 0^{- 14}$

5.3 Navier boundary condition of type two

Approximate solutions are given by $y (r) = \sum_{i = 0}^{N} y_{i} (r)$ , where N is natural number can be chosen to get the desired accuracy. We get the similar values of $y_{i} (r)$ as in example 5.1. The value of the constant a and the solutions $ϕ (r)$ are computed by using the boundary conditions $y^{'} (1) = 0$ , $ϕ^{'} (r) = y$ , and $ϕ (1) = 0$ respectively. Analogous remarks can be made as in example 5.1. Corresponding to this boundary condition The critical value of $λ_{0}$ can be approximated numerically to be 11.34. Maximum absolute residue error and approximate solutions are listed in Tables 5 and 6, Figures 5 and 6.

TABLE 5. Approximate lower solution and upper solution maximum absolute residual error corresponding to some positive

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
0	0	0	$1.24 \times 1 0^{- 14}$
7	$5.27 \times 1 0^{- 16}$	7	$9.32 \times 1 0^{- 15}$
11.34	$1.11 \times 1 0^{- 15}$	11.34	$1.77 \times 1 0^{- 15}$

TABLE 6. Approximate negative solution and positive solution maximum residual error of some negative

λ

$λ$	$\| \| E \| \|_{\infty}$	$λ$	$\| \| E \| \|_{\infty}$
$-$ 100	$1.95 \times 1 0^{- 14}$	$-$ 100	$2.97 \times 1 0^{- 12}$
$-$ 300	$1.42 \times 1 0^{- 14}$	$-$ 300	$8.34 \times 1 0^{- 4}$
$-$ 500	$1.98 \times 1 0^{- 13}$	$-$ 500	$1.68 \times 1 0^{- 3}$

6 CONCLUSION

We successfully applied this proposed technique on a third order non self adjoint ⁸^{(p. 58)} SBVP. Many authors^{20, 33, 34} have studied the convergence criteria by using Cauchy sequence. But, we proposed a new idea to prove the convergence analysis. We noticed that, our numerical results are very interesting. We conclude that, for each $- \infty < λ \leq λ_{0}$ , we always found two approximate solutions which are very close to their exact solutions. From residue table, we conclude that the approximate solutions converge very quickly to its exact solutions except positive solutions. The positive solutions converge to the exact positive solutions very slowly.

ACKNOWLEDGMENT

This work is supported by grant provided by DST project, file name: SB/S4/MS/805/12 and INSPIRE Program Division, file no. IF160984, Department of Science Technology, New Delhi, India-110016.

CONFLICT OF INTEREST

The authors declared no potential conflicts of interest with respect to the research, authorship, and publication of this article.

Biographies

Biswajit Pandit received his M.Sc. degree in mathematics and computing from IIT Guwahati, India, in 2016. He is currently a DST Inspire senior research fellow in the department of mathematics at IIT Patna. His research area of interest includes numerical analysis, epitaxial growth, monotone iterative technique, wavelets, ordinary, and partial differential equations.
Amit Kumar Verma earned his Ph.D. degree in Mathematics from IIT Kharagpur, India. He is currently working as an assistant professor in the department of mathematics at IIT Patna. His research area of interest includes numerical analysis, epitaxial growth, non-standard finite difference methods, monotone iterative technique, wavelets, integral transforms, ordinary, and partial differential equations.
Ravi P. Agarwal earned his Ph.D. (Mathematics) at the Indian Institute of Technology in Madras, India, one of the highest-ranking institutes of India. Currently, he is affiliated with the Department of Mathematics, Texas A&M University-Kingsville. Dr. Agarwal has been actively involved in research as well as pedagogical activities for the last 49 years. His major research interests include numerical analysis, differential and difference equations, inequalities, and fixed point theorems. He is an excellent scholar, dedicated teacher, and prolific researcher. He has published 45 research monographs and more than 1700 publications in prestigious national and international mathematics journals.

REFERENCES

1Barabasi AL, Stanley HE. Fractal Concepts in Surface Growth. Cambridge University Press; 1995.
10.1017/CBO9780511599798
Google Scholar
2Arthur JR. Molecular beam epitaxy. Surf Sci. 2002; 500: 189-217.
10.1016/S0039-6028(01)01525-4
CAS Web of Science® Google Scholar
3Escudero C, Hakl R, Peral I, Torres PJ. On radial stationary solutions to a model of nonequilibrium growth. Eur J Appl Math. 2013; 24: 437-453.
10.1017/S0956792512000484
Web of Science® Google Scholar
4 Kardar M, Parisi G, Zhang YC. Dynamic scaling of growing interfaces. Phys Rev Lett. 1986; 56: 889-892.
10.1103/PhysRevLett.56.889
CAS PubMed Web of Science® Google Scholar
5Chow B. On Harnack's inequality and entropy for the Gaussian curvature flow. Commun Pure Appl Math. 1991; 44: 469-483.
10.1002/cpa.3160440405
Web of Science® Google Scholar
6Escudero C, Korutcheva E. Origins of scaling relations in nonequilibrium growth. J Phys A Math Theor. 2012; 45: 1-14.
10.1088/1751-8113/45/12/125005
Web of Science® Google Scholar
7Escudero C, Peral I. Some fourth order nonlinear elliptic problem related to epitaxial growth. J Differ Equ. 2013; 254: 2515-2531.
10.1016/j.jde.2012.12.012
Web of Science® Google Scholar
8Zwillinger D. Handbook of Differential Equations. Academic Press; 1997.
Google Scholar
9Escudero C, Hakl R, Peral I, Torres PJ. Existence and nonexistence result for a singular boundary value problem arising in the theory of epitaxial growth. Math Methods Appl Sci. 2014; 37: 793-807.
10.1002/mma.2836
Web of Science® Google Scholar
10Verma AK, Pandit B. Existence and nonexistence results of radial solutions to singular BVPS arising in epitaxial growth theory; 2019. arXiv, 1911.04979.
Google Scholar
11Verma AK, Pandit B, Agarwal RP. On approximate stationary radial solutions for a class of boundary value problems arising in epitaxial growth theory. J Appl Comput Mech. 2019; 4: 712-734.
Google Scholar
12Verma AK, Pandit B, Escudero C. Numerical solutions for a class of singular boundary value problems arising in the theory of epitaxial growth. Eng Comput. 2019; 37: 2539-2560.
10.1108/EC-08-2019-0360
Web of Science® Google Scholar
13 Verma AK, Pandit B, Agarwal RP. On multiple solutions for a fourth order nonlinear singular boundary value problems arising in epitaxial growth theory. Math Methods Appl Sci. 2020.
10.1002/mma.6905
Web of Science® Google Scholar
14 Verma AK, Pandit B, Agarwal RP. Existence and nonexistence results for a class of fourth-order coupled singular boundary value problems arising in the theory of epitaxial growth. Math Methods Appl Sci. 2020.
10.1002/mma.6905
Web of Science® Google Scholar
15Singh M, Verma AK. An effective computational technique for a class of Lane-Emden equations. J Math Chem. 2016; 54: 231-251.
10.1007/s10910-015-0557-8
CAS Web of Science® Google Scholar
16Li XY, Wu BY. A novel method for nonlinear singular fourth order four-point boundary value problems. Comput Math Appl. 2011; 62: 27-31.
10.1016/j.camwa.2011.04.029
Web of Science® Google Scholar
17He JH. Homotopy perturbation technique. Comput Methods Appl Mech Eng. 1999; 178: 257-262.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
18Noor MA, Din STM. Homotopy perturbation method for solving sixth-order boundary value problems. Comput Math Appl. 2008; 55: 2953-2972.
10.1016/j.camwa.2007.11.026
Web of Science® Google Scholar
19Bota C, Căruntu B. Approximate analytical solutions of nonlinear differential equations using the least squares homotopy perturbation method. J Math Anal Appl. 2017; 448: 401-408.
10.1016/j.jmaa.2016.11.031
Web of Science® Google Scholar
20Ayati Z, Biazar J. On the convergence of homotopy perturbation method. J Egypt Math Soc. 2015; 23: 424-428.
10.1016/j.joems.2014.06.015
Google Scholar
21 He CH, Liu C, He JH, Shirazi AH, Sedighi HM. Passive atmospheric water harvesting utilizing an ancient Chinese ink slab and its possible applications in modern architecture. Facta Univ Mech Eng. 2020. doi:10.22190/FUME201203001H
Web of Science® Google Scholar
22Finlayson BA. The Method of Weighted Residuals and Variational Principles. Academic Press; 1972.
Google Scholar
23Anderson N, Arthurs AM. Complementary variational principles for diffusion problems with Michaelis-Menten kinetics. Bull Math Biol. 1980; 42: 131-135.
10.1007/BF02462371
Web of Science® Google Scholar
24Kirichenko VF, Krys'ko VA. Substantiation of the variational method in the theory of plates. Int Appl Mech. 1981; 17: 366-370.
Google Scholar
25Verma AK, Pandit B, Verma L, Agarwal RP. A review on a class of second order nonlinear singular BVPs. Mathematics. 2020; 8(7): 1045.
10.3390/math8071045
Web of Science® Google Scholar
26He JH. Homotopy perturbation method: a new nonlinear analytical technique. Appl Math Comput. 2003; 135: 73-79.
10.1016/S0096-3003(01)00312-5
Web of Science® Google Scholar
27He JH. Homotopy perturbation method for solving boundary value problems. Phys Lett A. 2006; 350: 87-88.
10.1016/j.physleta.2005.10.005
CAS Web of Science® Google Scholar
28He JH. Variational iteration method a kind of nonlinear analytical technique: some examples. Int J Non-Linear Mech. 1999; 34: 699-708.
10.1016/S0020-7462(98)00048-1
Web of Science® Google Scholar
29Abbaoui K, Cherruault Y. New ideas for proving convergence of decomposition methods. Comput Math Appl. 1995; 29(7): 103-108.
10.1016/0898-1221(95)00022-Q
Web of Science® Google Scholar
30Cherruault Y. Convergence of Adomian's method. Math Comput Model. 1990; 14(2): 83-86.
10.1016/0895-7177(90)90152-D
Google Scholar
31Ross KA. Elementary Analysis: The Theory of Calculus. Springer; 2013.
10.1007/978-1-4614-6271-2
Google Scholar
32Mathews JH, Fink KD. Nemerical Methods Using Matlab. Prentice Hall; 1999.
Google Scholar
33Biazar J, Ghazvini H. Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal Real World Appl. 2009; 10: 2633-2640.
10.1016/j.nonrwa.2008.07.002
Web of Science® Google Scholar
34Biazar J, Aminikhahb H. Study of convergence of homotopy perturbation method for systems of partial differential equations. Comput Math Appl. 2009; 58: 2221-2230.
10.1016/j.camwa.2009.03.030
Web of Science® Google Scholar

Citing Literature

All articles

Numerical approximations for a class of nonlinear higher order singular boundary value problem by using homotopy perturbation and variational iteration method

Abstract

1 INTRODUCTION

2 DESCRIPTION OF THE ITERATIVE METHODS

2.1 HPM

2.2 VIM

3 DERIVATION OF THE PROPOSED METHOD

4 CONVERGENCE ANALYSIS

5 NUMERICAL OBSERVATION

5.1 Dirichlet boundary condition

5.2 Navier boundary condition of type one

5.3 Navier boundary condition of type two

6 CONCLUSION

ACKNOWLEDGMENT

CONFLICT OF INTEREST

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical approximations for a class of nonlinear higher order singular boundary value problem by using homotopy perturbation and variational iteration method

Abstract

1 INTRODUCTION

2 DESCRIPTION OF THE ITERATIVE METHODS

2.1 HPM

2.2 VIM

3 DERIVATION OF THE PROPOSED METHOD

4 CONVERGENCE ANALYSIS

5 NUMERICAL OBSERVATION

5.1 Dirichlet boundary condition

5.2 Navier boundary condition of type one

5.3 Navier boundary condition of type two

6 CONCLUSION

ACKNOWLEDGMENT

CONFLICT OF INTEREST

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information