In this work, we have proposed a numerical approach for solving the incompressible Navier–Stokes equations in the streamfunction-vorticity formulation. The numerical scheme is based on the diagonally implicit fractional-step $θ -$ (DIFST) method used for the time discretization and the conforming finite element method for the spatial discretization. The accuracy and efficiency of the scheme are validated by solving some benchmark problems. The numerical simulations are carried out using the DUNE-PDELab open-source software package. The comparison of DIFST scheme with different time discretization schemes is provided in terms of CPU time. Also, different solvers with preconditioners are investigated for solving the resulting algebraic system of equations numerically.

1 INTRODUCTION

The numerical study of partial differential equations (PDEs) is central to a wide variety of applications in science, and engineering. They are employed to simulate the physical phenomena such as fluid flow, electrostatics, the propagation of heat or sound, elasticity, electrodynamics, and so forth. There is increasing interest in the numerical study of large-scale nonlinear PDEs, whose exact or approximate analytical solutions are difficult to calculate. Therefore, efficient and accurate numerical methods such as the finite element, the finite difference, the volume methods, and the spectral methods are some generally adopted numerical scheme for solving such equations. However, the finite difference methods give poor approximation between grid points while the finite element method use basis functions that are non-zero on small subdomains. Particularly, in computational fluid dynamics (CFD), the high-order finite element methods have gained greater attention in solving problems with complex geometries.¹ The CFD methods are becoming an important alternative to experiments for solving several fundamental and practical problems in fluid dynamics.² The incompressible Navier–Stokes equations (INSEs) are a system of PDEs that are fundamental in CFD.^{3, 4}

There are many numerical schemes available for solving the INSEs numerically in primitive variables. However, most of the methods require solving the pressure or pressure-correction Poisson equation, which serves to satisfy the continuity equation.⁵ Although, there are many alternative^{6, 7} but the streamfunction-vorticity formulation has the advantage of eliminating the pressure as a solution variable with mass conserving properties.^{8, 9} This formulation has also been used for image inpainting problems.¹⁰

In this work, the conforming finite element method^{11, 12} is used for solving the coupled vorticity transport and Poisson's equation simultaneously.^{13, 14} The DUNE-PDELab is used for the numerical simulations.^15-17 The PDELab is open-source software package for solving PDEs numerically and is based on Distributed and Unified Numerics Environment (DUNE).¹⁸

The structure of this article is as follows. In Section 2, the governing equations with appropriate initial and boundary conditions are given. Section 3 describes the variational formulation. Section 4 provides the resulting linear and nonlinear system of equation. Section 5 is based on the temporal discretization. In Section 6, numerical results and stability of the method are provided. The comparison of different solvers and preconditioner matrices are also given. Finally, Section 7 concludes this article.

2 PROBLEM STATEMENT

Consider the incompressible Navier–Stokes equation with streamfunction-vorticity formulation¹⁹;

\begin{align} ω_{t} + v \cdot \nabla ω & = ν Δ ω + f in Ω \times \sum, \sum = (t_{0}, t_{0} + T), \end{align}

()

\begin{align} ω & = - Δ ψ in Ω \times \sum, \end{align}

()

\begin{align} ω (\cdot, t) & = g (\cdot, t) on \partial Ω, \end{align}

()

\begin{align} ψ (\cdot, t) & = f (\cdot, t) on \partial Ω, \end{align}

()

\begin{align} ω (\cdot, t) & = ω_{0} (\cdot, t) at t = 0, \end{align}

()

\begin{align} ψ (\cdot, t) & = ψ_{0} (\cdot, t) at t = 0 . \end{align}

()

Here, $Ω \subset ℝ^{d}$ (d = 1, 2, 3) is a bounded domain with boundary $\partial Ω$ , $ψ$ is the streamfunction and $ω$ is the vorticity. Further, the $\nabla^{⊥} ψ = v$ is the fluid velocity, $ν$ is the kinematic viscosity, and f is external source term. The Dirichlet boundary conditions $g (\cdot, t)$ and $f (\cdot, t)$ are set for both components of coupled system on boundary $\partial Ω$ . Similarly, $ω_{0} (\cdot, t)$ and $ψ_{0} (\cdot, t)$ are initial conditions for both components, respectively.

3 WEAK FORMULATION

For the weak solution, the existence, uniqueness and consistency of solutions, that is, well-posedness in the Hadamard sense, is easier to prove.²⁰ After the multiplication of Equation (1a) with the test function $φ_{0}$ and Equation (1b) with the test function $φ_{1}$ and using integration by parts, we arrive at the weak formulation:

Find

(u_{0} (t), u_{1} (t)) \in U_{0} \times U_{1}

such that:

\begin{align} d_{t} {(u_{0}, φ_{0})}_{0, Ω} + {(v . \nabla u_{0}, φ_{0})}_{0, Ω} + ν {(\nabla u_{0}, \nabla φ_{0})}_{0, Ω} = {(f, φ_{0})}_{0, Ω}, \forall φ_{0} \in V_{0}, \end{align}

()

and

\begin{align} {(\nabla u_{1}, \nabla φ_{1})}_{0, Ω} - {(u_{0}, φ_{1})}_{0, Ω} = 0, \forall φ_{1} \in V_{1}, \end{align}

()

where the function spaces are given as follow;

U_{0} = {φ_{0} \in H^{1} (Ω) : φ_{0} = g on \partial Ω}, V_{0} = {φ_{0}, \in H^{1} (Ω) : φ_{0} = 0 on \partial Ω} .

Similarly,

U_{1} = {φ_{1} \in H^{1} (Ω) : φ_{1} = g on \partial Ω}, V_{1} = {φ_{1}, \in H^{1} (Ω) : φ_{1} = 0 on \partial Ω} .

We used the notation of the

L^{2}

inner product

{(u, φ)}_{0, Ω} = \int_{Ω} u φ d x

. An equivalent formulation to Equation (3) that hides the system structure reads as follows:

\begin{align} d_{t} {(u_{0}, φ_{0})}_{0, Ω} + {(\nabla^{⊥} u_{1} \cdot \nabla u_{0}, φ_{0})}_{0, Ω} + ν {(\nabla u_{0}, \nabla φ_{0})}_{0, Ω}. \\ - {(f, φ_{0})}_{0, Ω} + {(\nabla u_{1}, \nabla φ_{1})}_{0, Ω} - {(u_{0}, φ_{1})}_{0, Ω} = 0,. \\ \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1} .. \end{align}

()

Now, we identify the temporal and spatial residual forms from Equations (2) and (3) as follows;

Temporal residual form:

\begin{align} m^{N a v i e r} ((u_{0}, u_{1}), (φ_{0}, φ_{1})) = {(u_{0}, φ_{0})}_{0, Ω} . \end{align}

()

Spatial residual form:

\begin{align} r^{N a v i e r} ((u_{0}, u_{1}), (φ_{0}, φ_{1})) & = {(\nabla^{⊥} u_{1} \cdot \nabla u_{0}, φ_{0})}_{0, Ω} + ν {(\nabla u_{0}, \nabla φ_{0})}_{0, Ω} \\ - {(f, φ_{0})}_{0, Ω} + {(\nabla u_{1}, \nabla φ_{1})}_{0, Ω} - {(u_{0}, φ_{1})}_{0, Ω} . \end{align}

()

The spaces $U_{0}$ and $U_{1}$ can differ as different types of boundary conditions can be incorporated into the ansatz spaces. In this work, both the spaces are constrained by the same Dirichlet boundary conditions.

4 ALGEBRAIC PROBLEM

The conforming finite element method applied to Equation (4) is straightforward.²¹ We may use the conforming space

W_{h}^{k, d} (𝒯_{h})

of degree k in dimension d for each of the components. Typically, one would choose the same polynomial degree for both components. So we assume that any finite-dimensional space spanned by the basis function;

\begin{align} P_{h} = span {ψ_{1}, \dots, ψ_{i}}, Q_{h} = span {ϕ_{1}, \dots, ϕ_{j}}, \end{align}

We can reformulate the problem as;

\begin{align} u_{h} \in P_{h} = P_{h}^{1} \times \dots \times P_{h}^{s}, such that r_{h} (u_{h}, v) = 0, \forall v \in Q_{h} = Q_{h}^{1} \times \dots \times Q_{h}^{s}, \end{align}

()

where

“ s ”

is the number of components in the system. Expanding the solution

u_{h} = (\sum_{j = 1}^{n} {(y)}_{j} ψ_{j})

in the basis and hereby introducing the coefficient vector

y \in ℝ^{n}

. Now we formulate the problem as;

Find the

u_{h} \in U_{h}

such that:

r_{h} = (u_{h}, v) = 0,

\forall v \in Q_{h}

\begin{align} \Leftrightarrow r (\sum_{j = 1}^{n} {(y)}_{j} ψ_{j}, ϕ_{i}) = 0, \forall i = 1, \dots, m \\ \Leftrightarrow S (y) = 0, \end{align}

where

S : ℝ^{n} \to ℝ^{m}

given by

S_{i} (y) = r_{h} (\sum_{j = 1}^{n} {(y)}_{j} ϕ_{j}, ψ_{i})

is a nonlinear, vector-valued function,

m, n \in N

(the total number of vertices in a mesh) and

i, j \in I_{h}

(the index set of vertices). The solution of

S (y) = 0

which is the nonlinear algebraic system of equations is typically calculated by fixed point iteration of the form;

\begin{align} y^{(k + 1)} = y^{(k)} - λ^{k} H (y^{(k)}) S (y^{(k)}) . \end{align}

()

Here

H (y^{(k)})

is a preconditioner matrix and

λ^{k}

is a damping factor. For example, in the Newton's method,²²

\begin{align} H (y^{(k)}) = {(J (y^{(k)}))}^{- 1} with J {(y^{(k)})}_{i, j} = \frac{\partial S_{i}}{\partial y_{j}} (y^{(k)}) . \end{align}

We assumed that $n = m$ so that the Jacobian matrix $J (y^{(k)})$ is invertible. The Newton's method needs the solution of the linear system $J (y^{(k)}) w = S (y^{(k)})$ in each iteration. So, the resulting linear system can either be solved by direct or iterative linear solvers. In this work, different iterative solvers with various preconditioners are tested as given in Table 3.

5 TEMPORAL DISCRETIZATION

In this section, we discuss the discretization of the temporal part of Equation (2). For the unsteady part, let

u_{0} \in L_{2} (t_{0}, t_{0} + T; u_{0 g} + V_{0} \times V_{1} (t))

\begin{align} d_{t} {(u_{0}, φ_{0})}_{0, Ω} + {(v . \nabla u_{0}, φ_{0})}_{0, Ω} + ν {(\nabla u_{0}, \nabla φ_{0})}_{0, Ω} + {(\nabla u_{1}, \nabla φ_{1})}_{0, Ω}. \\ - {(u_{0}, φ_{1})}_{0, Ω} + {(f, ϕ_{0})}_{0, Ω} = 0, \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1} (t) \in \sum, t \in \sum,. \end{align}

()

where

V_{0} \times V_{1} (t) = {(φ_{0}, φ_{1}) \in H^{1} (Ω) : (φ_{0}, φ_{1}) = 0 on \partial Ω}

. The initial condition

u_{0}

is a function of

x \in Ω

. In a more compact way, this can be written with residual forms Equations (5) and (6) as follows:

\begin{align} d_{t} m^{N a v i e r} (u_{0}, φ_{0}; t) + r^{N a v i e r} [(u_{0}, u_{1}), (φ_{0}, φ_{1}); t] = 0, \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1}, t \in \sum, \end{align}

where,

\frac{d}{d t}

is time derivative and

r^{N a v i e r} [(u_{0}, u_{1}), (φ_{0}, φ_{1}); t]

depend on time residual form, and the new temporal residual form is

m (u_{0}, φ_{0}; t) = \int_{Ω} u_{0} φ_{0} d x

. We opted the conforming finite element space

W_{h}^{k, d} (𝒯_{h})

of degree k and the function

u_{0 h, g} (t)

, which depends on time, such that

u_{0 h} (t) \in U_{0 h} (t) = u_{0 h, g} (t) + U_{0 h} \times U_{1 h} (t)

. Therefore, the spatial and temporal residual forms can be approximated as

m^{N a v i e r} (u_{0}, φ_{0}; t) \approx m_{h}^{N a v i e r} (u_{0 h}, φ_{0 h}; t)

and

r^{N a v i e r} [(u_{0}, u_{1}), (φ_{0}, φ_{1}); t] \approx r_{h}^{N a v i e r} [(u_{0 h}, u_{1 h}), (φ_{0 h}, φ_{1 h}); t],

respectively. Now, we take the system of ordinary differential equations (ODEs) for the integration, divide the time interval to sub-interval which are not necessarily equidistant that is,

\begin{align} \sum^{‾} = {t^{0}} \cup (t^{0}, t^{1}] \cup \dots \cup (t^{N - 1}, t^{N}], \end{align}

with

t^{0} = t_{0}

t^{N} = t_{0} + T

t^{k - 1} < t^{k}

for

1 \leq k \leq N

and set the time-step to

Δ t^{k} = t^{k + 1} - t^{k}

One of the simplest ODEs solver is the one-step- $θ$ method²³ that reads:

Find

u_{0 h}^{k + 1} \in U_{0 h} (t^{k + 1})

such that:

\begin{align} \frac{1}{Δ t^{k}} (m_{h}^{N a v i e r} (u_{0 h}^{k + 1}, φ_{0}; t^{k + 1}) - m_{h}^{N a v i e r} (u_{0 h}^{k}, φ_{0}; t^{k})) + θ r_{h}^{N a v i e r} [(u_{0 h}^{k}, u_{1 h}^{k}), (φ_{0}, φ_{1}); t^{k}] \\ + (1 - θ) r_{h}^{N a v i e r} [(u_{0 h}^{k + 1}, u_{1 h}^{k + 1}), (φ_{0}, φ_{1}); t^{k + 1}] = 0, \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1} (t^{k + 1}) . \end{align}

()

By rearranging the terms of Equation (11), leads to the solution of a nonlinear system with the same structure as before at each time-step.²⁴

Find

u_{0 h}^{k + 1} \in U_{0 h} (t^{k + 1})

such that;

\begin{align} \frac{1}{Δ t^{k}} (m_{h} (u_{0 h}^{k + 1}, φ_{0}; t^{k + 1}) - m_{h} (u_{0 h}^{k}, φ_{0}; t^{k})) + θ r_{h} [(u_{0 h}^{k}, u_{1 h}^{k}), (φ_{0}, φ_{1}); t^{k}] \\ + (1 - θ) r_{h} [(u_{0 h}^{k + 1}, u_{1 h}^{k + 1}), (φ_{0}, φ_{1}); t^{k + 1}] = 0, \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1} (t^{k + 1}) . \end{align}

()

By rearranging the terms of Equation (11), leads to the solution of a nonlinear system with the same structure as before at each time-step.²⁴

Find

u_{0 h}^{k + 1} \in U_{0 h} (t^{k + 1})

such that;

\begin{align} m_{h}^{N a v i e r} (u_{0 h}^{k + 1}, φ_{0}; t^{k + 1}) + Δ t^{k} θ r_{h}^{N a v i e r} [(u_{0 h}^{k}, u_{1 h}^{k}), (φ_{0}, φ_{1}); t^{k}] - m_{h}^{N a v i e r} (u_{0 h}^{k}, φ_{0}; t^{k}). \\ + Δ t^{k} (1 - θ) r_{h}^{N a v i e r} [(u_{0 h}^{k + 1}, u_{1 h}^{k + 1}), (φ_{0}, φ_{1}); t^{k + 1}] = 0, \forall (φ_{0}, φ_{1}) \in V_{0} \times V_{1} (t^{k + 1}) .. \end{align}

()

The residual form Equation (12) consists of a linear combination of spatial and of temporal residual forms.

The Runge–Kutta method:

The temporal and spatial residual form can be written as follows^{25, 26}:

$u_{0 h}^{(0)} = u_{0 h}^{k}$ .
For $i = 1, \dots, s \in ℕ$ , find $u_{0 h}^{(i)} \in u_{0 h, g} (t^{k} + d_{i} Δ t^{k}) + U_{0 h} (t^{k + 1})$ :
$\begin{align} \sum_{j = 0}^{s} (\begin{array}{c} a_{i j} m_{h} (u_{0 h}^{(j)}, φ_{0}; t^{k} + d_{j} Δ t^{k}) +. \\ b_{i j} Δ t^{k} r_{h} ((u_{0} h, u_{1} h), (φ_{0} h, φ_{1} h); t^{k} + d_{j} Δ t^{k}). \end{array}) & = 0, \\ \forall (φ_{0}, φ_{1}) & \in V_{0} \times V_{1} (t^{k + 1}) . \end{align}$
$u_{0 h}^{k + 1} = u_{0 h}^{(s)}$ .

Here, we suppose that the same type of boundary condition hold through

(t^{k}, t^{k + 1}]

. The

s -

stage scheme is given by:

\begin{align} A = [\begin{array}{ccc} p_{10} & \dots & p_{1 s} \\ ⋮ & ⋮ \\ p_{s 0} & \dots & p_{s s} \end{array}], B = [\begin{array}{ccc} q_{10} & \dots & q_{1 s} \\ ⋮ & ⋮ \\ q_{s 0} & \dots & q_{s s} \end{array}], d = {(d_{0}, \dots, d_{s})}^{T} . \end{align}

The explicit schemes are characterized by $p_{i j} = 0$ for $j > i$ and $q_{i j} = 0$ for $j \geq i$ . The diagonally implicit schemes are characterized by $p_{i j} = q_{i j} = 0$ for $j > i$ . Without loss of generality it can be assumed that $p_{i i} = 1$ . Moreover, some diagonally implicit schemes, implemented in this work satisfy $q_{i i} = b \forall i$ .

The Shu–Osher form of Runge–Kutta explicit methods and most implicit Runge–Kutta methods may be brought to the form:

One step $θ -$ scheme:
$\begin{align} A = [\begin{array}{cc} - 1 & 1 \end{array}], B = [\begin{array}{cc} 1 - θ & θ \end{array}], d = {(0, 1)}^{T} . \end{align}$
For the explicit/implicit Euler scheme ( $θ \in {0, 1}$ ) and for the Crank–Nicolson scheme ( $θ = \frac{1}{2}$ ).
Heun's second-order explicit method
$\begin{align} A = [\begin{array}{ccc} - 1 & 1 & 0 \\ - \frac{1}{2} & - \frac{1}{2} & 1 \end{array}], B = [\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \end{array}], d = {(0, 1, 1)}^{T} . \end{align}$
Alexander's two-stage second-order strongly S-stable method²⁷:
$\begin{align} A = [\begin{array}{ccc} - 1 & 1 & 0 \\ - 1 & 0 & 1 \end{array}], B = [\begin{array}{ccc} 0 & α & 0 \\ 0 & 1 - α & α \end{array}], d = {(0, α, 1)}^{T} \end{align}$
with $α = 1 - \frac{\sqrt{2}}{2}$ .
Fractional step $θ -$ scheme²⁸:
$\begin{align} A = [\begin{array}{rrrr} - 1 & 1 & 0 & 0 \\ 0 & - 1 & 1 & 0 \\ 0 & 0 & - 1 & 1 \end{array}], B = [\begin{array}{rrrr} θ (1 - α) & θ α & 0 & 0 \\ 0 & θ^{'} α & θ^{'} (1 - α) & 0 \\ 0 & 0 & θ (1 - α) & θ α \end{array}], \end{align}$

$\begin{align} d = {(0, θ, 1 - θ, 1)}^{T}, \end{align}$
three stage second order strongly A-stable scheme. With $θ = 1 - \frac{\sqrt{2}}{2}$ , $α = 2 θ$ , $θ^{'} = 1 - 2 θ = 1 - α = \sqrt{2} - 1$ . Note also that $θ α = θ^{'} (1 - α) = 2 θ^{2}$ .

With $θ$ = $1 - \frac{1}{2} \sqrt{2}$ , the damped Newton method is used to solve the nonlinear system, while we used different linear solvers with preconditioners to solve the resulting system of linear equations.

6 NUMERICAL RESULTS

In this section, the computed results for some test problems are provided.

6.1 Test problem 1:

A test problem in the square domain

0 \leq x, y \leq 1

with an exact solution is chosen with the initial condition as¹⁹;

\begin{align} ω (x, y, 0) = 4 c (y^{2} - 1) (y^{2} - 8) \sin 2 x - \frac{12 c}{100} (y^{2} - 1), \end{align}

()

\begin{align} ψ (x, y, 0) = 0.1 (y^{2} - 1) (y^{2} - 5) (\sin 2 x + \frac{1}{100}) . \end{align}

()

For finding the accuracy of the method, f, b, and c are chosen such that the Equations (1a) and (1b) have the following exact solution;

\begin{align} ω (x, y, t) = 4 c e^{b t} (y^{2} - 1) (y^{2} - 8) \sin 2 x - \frac{12 c}{100} e^{b t} (y^{2} - 1), \\ ψ (x, y, t) = c e^{b t} (y^{2} - 1) (y^{2} - 5) (\sin 2 x + \frac{1}{100}) . \end{align}

()

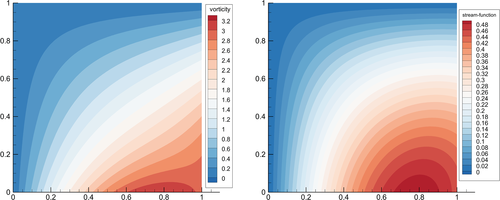
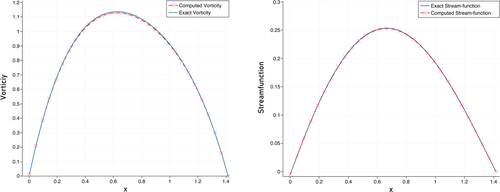
For the purpose of numerical simulation, we have chosen $b = c = 0.1$ , $N = 33$ , and $Δ t = 0.005$ . The computed results given in Tables 1 and 2 are obtained by using the combination of DIFST scheme, Newton's method and preconditioned SSOR BiCG-Stab for time discretization, nonlinear and linear solvers respectively. The computed solutions are shown in Figure 1A,B at time $T = 3$ and $ν = 0.01$ . In Figure 2, plots over the line are shown for comparison of the computed and exact solutions and a very good agreement is observed.

TABLE 1.

L^{2} -

error and convergence rates for different numbers of iterations (ITs) of the streamfunction

(ψ (t))

T	b = c	Linear ITs	Nonlinear ITs	$L^{2} -$ error	CPU time (s)
2.0	0.1	14905	14905	1.0712E-03	1.8352e+01
2.5	0.1	17963	17963	3.9923E-04	1.2694e+01
3.0	0.1	21035	21035	1.4879E-04	2.7985e+01
3.5	0.1	23873	23873	5.5456E-05	3.2656e+01
4.0	0.1	26845	26845	2.0668E-05	3.7321e+01
4.5	0.1	29843	29843	7.7027E-06	4.1962e+01
5.0	0.1	32871	32871	2.8712E-07	4.6629e+01

TABLE 2.

L^{2} -

error and convergence rates for different numbers of iterations (ITs) of the vorticity

(ω (t))

T	b = c	Linear ITs	Nonlinear ITs	$L^{2} -$ error	CPU time (s)
2.0	0.1	14905	14905	2.1144E-02	1.8352e+01
2.5	0.1	17963	17963	7.8807E-03	1.2694e+01
3.0	0.1	21035	21035	2.9371E-03	2.7985e+01
3.5	0.1	23873	23873	1.0946E-03	3.2656e+01
4.0	0.1	26845	26845	4.0799E-04	3.7321e+01
4.5	0.1	29843	29843	1.5206E-04	4.1962e+01
5.0	0.1	32871	32871	5.6677E-05	4.6629e+01

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Contour plots for computed (A) vorticity and (B) streamfunction

Table 3 contains the solution of Equations (1a) and (1b) with different linear solvers. In this study, two different linear solvers and four preconditioners were employed as given in Table 3. The bi-conjugate gradient stabilized (BiCG-stab) method with symmetric successive over relaxation (SSOR) preconditioner gives the less number of iterations, followed by the conjugate gradient (CG) method with SSOR as a preconditioner. However, BiCG-stab with the Jacobi method as preconditioner is also promising with 15 number of iterations. The CG method with a Jacobi preconditioner produced 30 number of iterations and lastly the BiCG-stab method with Richardson as preconditioner has the largest number of iterations. Furthermore, with regards to the computational time, the BiCG-stab with SSOR has the less CPU time, followed by CG with Jacobi, the BiCG-stab with Jacobi, CG with SSOR, and lastly the BiCG-stab with Richardson. In terms of accuracy, we computed the

L^{2} -

error and observed that the BiCG-stab solver with a SSOR preconditioner gives best accuracy, followed by the CG method with SSOR, BiCG-stab with Jacobi, CG with Jacobi, and in last BiCG-stab with Richardson as a preconditioner. The grid refinement results and orders of accuracy for the proposed scheme are shown in Table 4. The following formula is used to determine the order of accuracy

O_{A}

\begin{align} O_{A} = \frac{\ln (e_{1} / e_{2})}{\ln 2}, \end{align}

where

\begin{align} e_{1} = ϕ_{e} - ϕ_{f} e_{2} = ϕ_{e} - ϕ_{c} \end{align}

TABLE 3. Comparison for number of iterations, computational costs (in seconds(s)) and

L^{2} -

error of different linear solver with preconditioners

Solver	Preconditioner	Iterations	CPU time (s)	$L^{2} -$ error $(ψ (t))$
BiCG-Stab	Jacobi	15	0.006268	3.1844E-06
CG	SS0R	14	0.004509	2.9437E-06
BiCG-Stab	SSOR	10	0.003774	2.8712E-07
CG	Jacobi	30	0.005511	4.0760E-06
BiCG-Stab	Richardson	224	0.031864	7.6456E-06

TABLE 4. Convergence rate for the

L^{2} -

error

Grid size	$L^{2} -$ error	$O_{A}$
32 $\times$ 32	1.26E-02	–
64 $\times$ 64	1.56E-03	3.01
128 $\times$ 128	1.91E-04	3.02
256 $\times$ 256	2.26E-05	3.07
512 $\times$ 512	2.83E-06	2.99

The exact solution is $ϕ_{e}$ , the solution on a fine grid is $ϕ_{f}$ , and the solution on a coarse grid is $ϕ_{c}$ . It is shown that the order of accuracy for the proposed scheme is 3.

6.1.1 Numerical stability:

Next, we discuss the numerical stability of the different time discretization schemes. All these results are taken by keeping viscosity fixed $ν = 0.01$ , number of nodes $N = 33$ and with different values of $Δ t$ from time $T = 0$ to $T = 3$ . In Table 5, the computational cost is presented in terms of CPU time. We have observed that diagonally implicit fractional-step $θ$ scheme is more efficient and stable, while the explicit schemes are unstable for $Δ t \geq 1 0^{- 4} .$

TABLE 5. Computational costs (in seconds(s)) for different time discretization schemes

Scheme	$Δ t = 1 0^{- 4}$	$Δ t = 1 0^{- 3}$	$Δ t = 1 0^{- 2}$	$Δ t = 1 0^{- 1}$
DIFST	1.1947e+02	1.1157e+01	1.1068e+00	1.1513e−01
Implicit Euler	3.6316e+02	3.7706e+01	3.9438e+00	3.8905e $-$ 01
Crank Niklson	1.1859e+03	1.1848e+02	1.1743e+01	1.2086e+00
Alexander (order 2)	8.0120e+02	7.6602e+01	7.5474e+00	7.7801e $-$ 01
Alexander (order 3)	1.1362e+03	1.1475e+02	1.1448e+01	1.1779e+00
Heun's	Fails	Fails	Fails	Fails
Shu third-order	Fails	Fails	Fails	Fails

6.2 Test problem 2: The Taylor–Green vortex problem

We consider the two dimensional Taylor-Green vortex problem in the square domain,

Ω = {(0, 2 π)}^{2}

.²⁹ The exact solution is;

\begin{align} ω (x, y, t) = - 2 \cos x \cos y e^{- 2 ν t}, \end{align}

()

and

\begin{align} ψ (x, y, t) = - \cos x \cos y e^{- 2 ν t} . \end{align}

()

The initial conditions are

\begin{align} ω (x, y, 0) = - 2 \cos x \cos y, \end{align}

()

and

\begin{align} ω (x, y, 0) = - \cos x \cos y . \end{align}

()

The periodic boundary conditions are imposed in both the x and y directions. The source term is given by $f = 0$ . For this problem, we show the results for the $ν = 0.01$ , $Δ x = 0.005$ and time $T = 1$ . The comparison between the computed results are shown in Figures 3 and 4 which shows the good agreement with the exact solution. The computed results given in Tables 6 and 7 are obtained by using the combination of DIFST scheme, Newton's method and preconditioned SSOR BiCG-stab for time discretization, nonlinear and linear solvers respectively.

TABLE 6.

L^{2} -

error and convergence rates for different numbers of iterations (ITs) of the streamfunction

(ψ (t))

$T$	$ν$	Linear ITs	Nonlinear ITs	$L^{2} -$ error	CPU time (s)
2.0	0.01	2237	2237	1.3174E-03	4.9459e+00
2.5	0.01	2790	2790	3.7607E-04	6.1735e+00
3.0	0.01	3357	3357	3.9371E-05	7.3951e+00
3.5	0.01	3924	3924	1.7006E-05	8.6268e+00
4.0	0.01	4484	4484	2.0979E-06	9.8551e+00
4.5	0.01	5044	5044	5.2207E-07	1.1071e+01
5.0	0.01	5603	5603	6.4533E-07	1.2297e+01

TABLE 7.

L^{2} -

error and convergence rates for different numbers of iterations (ITs) of the vorticity

(ω (t))

$T$	$ν$	Linear ITs	Nonlinear ITs	$L^{2} -$ error	CPU time (s)
2.0	0.01	2237	2237	1.2364E-02	4.9459e+00
2.5	0.01	2790	2790	1.0807E-03	6.1735e+00
3.0	0.01	3357	3357	3.0361E-04	7.3951e+00
3.5	0.01	3924	3924	1.7649E-05	8.6268e+00
4.0	0.01	4484	4484	2.0789E-06	9.8551e+00
4.5	0.01	5044	5044	1.4256E-06	1.1071e+01
5.0	0.01	5603	5603	1.0012E-06	1.2297e+01

6.3 Test problem 3: 2D Lid driven cavity flow

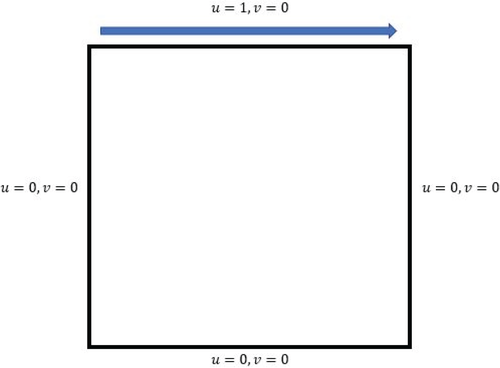
In the following problem, the flow is given by moving the top lid boundary with constant speed $u = 1$ with no-slip boundary conditions on the other walls of square domain while the pressure is extrapolated from the interior. The configuration of geometry and boundary condition are shown in Figure 5. The computational domain for this problem is a square with edges of unit length.

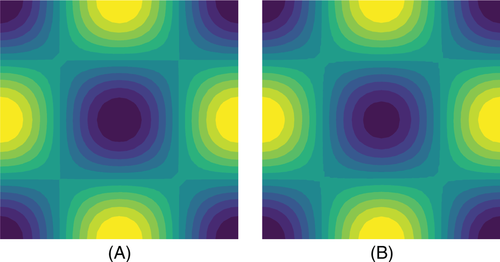
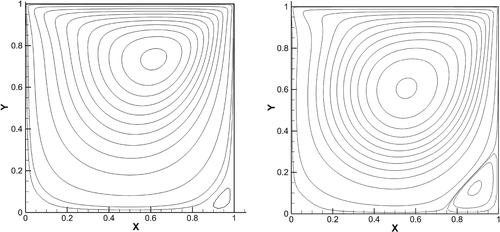
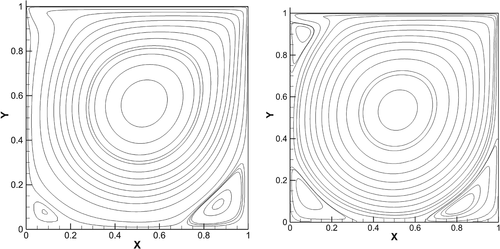
In Figure 6A,B, the vorticity contours at $T = 25$ for $R e = 100$ and $R e = 400$ are given. Similarly, in Figure 7A,B, the vorticity contours at $T = 25$ for $R e = 1000$ and $R e = 5000$ are given. We observed both results have shown good agreement especially in terms of computational cost with the existing results in literature .

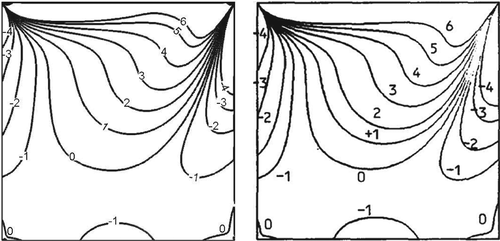
In Figure 8A,B, the comparison of vorticity contours at $T = 25$ for $R e = 100$ are given which shows the good agreement with result in Reference 30.

6.3.1 Numerical stability:

Next, we discuss the numerical stability of the different time discretization schemes. All these results are taken by keeping viscosity fixed $ν = 0.001$ , with $Δ t = 0.25$ and from time $T = 0$ to $T = 25$ . In Table 8, the computational cost is presented in terms of CPU time. We have observed that DIFST scheme is more efficient and stable.

TABLE 8. Computational costs (in seconds(s)) of different schemes for different number of iterations

Scheme	CPU time ( $Δ t = 0.25$ )	Linear ITs	Nonlinear ITs
DIFST	2.0188e+02	12245	245
One step $θ$	2.2251e+02	13467	298
Crank Niklson	2.1230e+02	20261	307
Alexander (order 2)	3.8680e+02	21307	516
Alexander (order 3)	7.2525e+03	34532	749
Heun's	Fails	Fails	Fails
Shu third-order	Fails	Fails	Fails

7 CONCLUSIONS

This article presents a numerical scheme for solving the two-dimensional unsteady incompressible Navier–Stokes equations by using the conforming finite element method. The diagonally implicit fractional step $θ -$ scheme for the temporal discretization is used. By the damped Newton method, the non-linear system of equation is solved. While the linear system of equations is solved by implementing different linear solver with preconditioners. It is observed that BiCG-stab with preconditioner SSOR gave efficient results based on the number of iterations and $L^{2} -$ error. The accuracy of the scheme is given by computing the $L^{2} -$ error norm. For the time-dependent solution, the robustness and efficiency of the DIFST scheme are demonstrated by comparing it with other time discretization schemes. A comparison of different linear solvers with preconditioners are given in terms of the number of iterations, the $L^{2} -$ error norm and CPU time. The DUNE-PDELab open source software is used for all the numerical computations.

ACKNOWLEDGMENTS

Part of this work was carried out during the visit of S. Raza to the University of Heidelberg under the Post-Bachelor program of HGS MATHCOMP. The support of Prof. Peter Bastian and Mr. Linus Seelinger from IWR is highly acknowledged. The work of A. Shah, A. Rauf was supported by HEC under NRPU No. 7781 and S. Raza by PSF No. 5651.

CONFLICT OF INTEREST

The authors declare no potential conflict of interests.

Biographies

Saad Raza received MS and BS in Mathematics from COMSATS University Islamabad, Pakistan. Currently, he is working as Research Assistant in the Department of Mathematics, COMSATS University Islamabad, Pakistan. His research interests is in Applied $&$ Computational Mathematics and Numerical solution of Partial Differential Equations.
Abdul Rauf was a research student at COMSATS University in Islamabad, Pakistan. He does research on numerical techniques for solving systems of nonlinear equations and partial differential equations.
Jamilu Sabi'u is a research student at COMSATS University in Islamabad, Pakistan. He does research on numerical techniques for solving systems of nonlinear equations and partial differential equations. He had almost 30 publications published in reputable journals.
Dr. Abdullah Shah received PhD in Computational Mathematics from Institute of Computational Mathematics, Scientific/Engineering Computing, Chinese Academy of Sciences in 2008. Currently, he is working as Head and Associate Professor in the Department of Mathematics, COMSATS University Islamabad, Pakistan and involved in teaching, research, and administration. His research interests span Applied $&$ Computational Mathematics, Modeling $&$ Simulations, and Computational Fluid Dynamics. He is the author of several research articles published in reputed journals. Also, he is the recipient of prestigious Erasmus Mundus (EMMA) postdoctoral fellowship at Interdisciplinary Center for Scientific Computing (IWR), University of Heidelberg, Germany, in 2014, "TWAS-UNESCO Associate" (2013–2016) and CAS President's International Fellowship Initiative "Visiting Scientist" (2018–2019) at Chinese Academy of Sciences. He is HEC approved supervisor in mathematics and supervising BS/MS and PhD students.

REFERENCES

1Chen S, Tölke J, Krafczyk M. A new method for the numerical solution of vorticity-streamfunction formulations. Comput Methods Appl Mech Eng. 2008; 198: 367-376.
10.1016/j.cma.2008.08.007
Web of Science® Google Scholar
2Shui Q. Penalty and characteristic-based operator splitting with multistep scheme finite element method for unsteady incompressible viscous flows. Prog Comput Fluid Dyn Int J. 2020; 20(3): 125-142.
10.1504/PCFD.2020.107275
Web of Science® Google Scholar
3Shah A, Yuan L. Upwind compact finite difference scheme for time-dependent incompressible Navier-Stokes equations. Appl Math Comput. 2010; 215(9): 3201-3213.
10.1016/j.amc.2009.10.001
Web of Science® Google Scholar
4Shah A, Guo H, Yuan L. A third-order upwind compact scheme on curvilinear meshes for the incompressible Navier-Stokes equations. Commun Comput Phys. 2009; 5(2-4): 712-729.
Web of Science® Google Scholar
5Shah A, Yuan L. Flux-difference splitting-based upwind compact schemes for the incompressible Navier–Stokes s. Int J Numer Methods Fluids. 2009; 61: 552-568.
10.1002/fld.1965
Web of Science® Google Scholar
6Granados JM, Bustamante CA, Power H, Flórez WF. A global Stokes method of approximated particular solutions for unsteady two-dimensional Navier–Stokes system of equations. Int J Comput Math. 2017; 94: 1515-1541.
10.1080/00207160.2016.1210795
Web of Science® Google Scholar
7Anaya V, Mora D, Reales C, Ruiz-Baier R. Mixed methods for a stream-function-vorticity formulation of the axisymmetric Brinkman equations. J Sci Comput. 2017; 71(1): 348-364.
10.1007/s10915-016-0302-x
Web of Science® Google Scholar
8Ghadi F, Ruas V, Wakrim M. Finite element solution of a stream function-vorticity system and its application to the Navier Stokes equations. Appl Math. 2013; 04(01): 257-262.
10.4236/am.2013.41A039
Google Scholar
9Ramšak M, Škerget L, Hriberšek M, Žunič Z. A multidomain boundary element method for unsteady laminar flow using stream function-vorticity s. Eng Anal Bound Elem. 2005; 29: 1-14.
10.1016/j.enganabound.2004.09.002
Web of Science® Google Scholar
10Bertalmio M, Bertozzi AL, Sapiro G. Navier-stokes, fluid dynamics, and image and video inpainting. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR; 2001:I.
Google Scholar
11Schroeder PW, Lube G. Pressure-robust analysis of divergence-free and conforming FEM for evolutionary incompressible Navier–Stokes flows. J Numer Math. 2017; 25(4): 249-276.
10.1515/jnma-2016-1101
Web of Science® Google Scholar
12Bonito A, Demlow A, Licht M. A divergence-conforming finite element method for the surface Stokes equation. SIAM J Numer Anal. 2020; 58(5): 2764-2798.
10.1137/19M1284592
Web of Science® Google Scholar
13Huang JJ, Huang H, Wang SL. Phase-field-based simulation of axisymmetric binary fluids by using vorticity-streamfunction formulation. Prog Comput Fluid Dyn Int Aust Dent J. 2015; 15(6): 352-371.
10.1504/PCFD.2015.072776
CAS Web of Science® Google Scholar
14Winslow AM. Numerical solution of the quasilinear Poisson in a nonuniform triangle mesh. J Comput Phys. 1966; 1: 149-172.
10.1016/0021-9991(66)90001-5
Google Scholar
15Bastian P, Blatt M. On the generic parallelisation of iterative solvers for the finite element method. Int J Comput Sci Eng. 2008; 4: 56-69.
Google Scholar
16Sabir M, Shah A, Muhammad W, Ali I, Bastian P. A mathematical model of tumor hypoxia targeting in cancer treatment and its numerical simulation. Comput Math with Appl. 2017; 74(12): 3250-3259.
10.1016/j.camwa.2017.08.019
Web of Science® Google Scholar
17Shah A, Sabir M, Bastain P. An efficient time-stepping scheme for numerical simulation of dendritic crystal growth. Eu J Comput Mech. 2017; 25(6): 475-488.
10.1080/17797179.2016.1276395
Web of Science® Google Scholar
18Alkämper M, Langer A. Using DUNE-ACFem for non-smooth minimization of bounded variation functions. Arch Numer Softw. 2017; 5: 3-19.
Google Scholar
19Li J, Sun W. Spectral method of decoupling the vorticity and stream function for the incompressible fluid flows. Comput. Math with Appl. 1999; 37: 35-40.
10.1016/S0898-1221(98)00239-9
Web of Science® Google Scholar
20 Koch H, Lasiecka I. Hadamard well-posedness of weak solutions in nonlinear dynamic elasticity-full von Karman systems. In: Lorenzi A, Ruf, B (eds) Evolution Equations, Semigroups and Functional Analysis. Springer; 2002: 197-216.
10.1007/978-3-0348-8221-7_11
Web of Science® Google Scholar
21 Silvester DJ, Wathen AJ. Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics. Numeric Mathematics and Scientific Computation. Oxford University Press; 2005.
Google Scholar
22 Long YQ, Cen S, Long ZF. Advanced Finite Element Method in Structural Engineering. Tsinghua University Press; 2009.
10.1007/978-3-642-00316-5
Web of Science® Google Scholar
23 Butcher JC, Goodwin N. Numerical Methods for Ordinary Differential Equations. Wiley; 2008.
10.1002/9780470753767
Google Scholar
24Gu TX, Zuo XY, Liu XP, Li PL. An improved parallel hybrid bi-conjugate gradient method suitable for distributed parallel computing. J Comput Appl Math. 2009; 226(1): 55-65.
10.1016/j.cam.2008.05.017
Web of Science® Google Scholar
25Shu CW, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J Comput Phys. 1988; 77(2): 439-471.
10.1016/0021-9991(88)90177-5
Web of Science® Google Scholar
26 Gottlieb S, Ketcheson DI, Shu CW. Strong Stability Preserving Runge-Kutta and Multistep Time Discretizations. World Scientific; 2011.
10.1142/7498
Google Scholar
27Kennedy CA, Mark H. Diagonally implicit Runge–Kutta methods for stiff ODEs. Appl Numer Math. 2019; 146: 221-244.
10.1016/j.apnum.2019.07.008
Web of Science® Google Scholar
28Meidner D, Richter T. A posteriori error estimation for the fractional step theta discretization of the incompressible Navier–Stokes equations. Comput Methods Appl Mech Eng. 2015; 1(288): 45-59.
10.1016/j.cma.2014.11.031
Web of Science® Google Scholar
29Chorin AJ. Numerical solution of the Navier-Stokes equations. Math Comput. 1968; 22(104): 745-762.
10.1090/S0025-5718-1968-0242392-2
Web of Science® Google Scholar
30Ghia U, Ghia KN, Shin CT. High re solutions for incompressible Navier-Stokes equations. J Comput Phys. 1983; 49: 387-411.
Google Scholar

Citing Literature

All articles

A numerical method for solution of incompressible Navier–Stokes equations in streamfunction-vorticity formulation

Abstract

1 INTRODUCTION

2 PROBLEM STATEMENT

3 WEAK FORMULATION

4 ALGEBRAIC PROBLEM

5 TEMPORAL DISCRETIZATION