Computational and Mathematical Methods
Volume 3, Issue 6 e1176
SPECIAL ISSUE PAPER
Full Access

Two derivative-free algorithms for constrained nonlinear monotone equations

Auwal Bala Abubakar, 

Corresponding Author

Auwal Bala Abubakar

Department of Mathematical Sciences, Faculty of Physical Science, Bayero University Kano, Kano, Nigeria

Numerical Optimization Research Group, Bayero University Kano, Kano, Nigeria

Department of Mathematics and Applied Mathematics, Sefako Makgatho Health Sciences University, Ga-Rankuwa, South Africa

Correspondence Auwal Bala Abubakar, Department of Mathematical Sciences, Faculty of Physical Science, Bayero University Kano, Kano, Nigeria.

Email: [email protected]

Search for more papers by this author
Hassan Mohammad, 

Hassan Mohammad

Department of Mathematical Sciences, Faculty of Physical Science, Bayero University Kano, Kano, Nigeria

Numerical Optimization Research Group, Bayero University Kano, Kano, Nigeria

Search for more papers by this author
Mohammed Yusuf Waziri, 

Mohammed Yusuf Waziri

Department of Mathematical Sciences, Faculty of Physical Science, Bayero University Kano, Kano, Nigeria

Numerical Optimization Research Group, Bayero University Kano, Kano, Nigeria

Search for more papers by this author
First published: 15 May 2021
https://doi.org/10.1002/cmm4.1176

Abstract

We propose two positive parameters based on the choice of Birgin and Martínez search direction. Using the two classical choices of the Barzilai-Borwein parameters, two positive parameters were derived by minimizing the distance between the relative matrix corresponding to the propose search direction and the scaled memory-less Broyden–Fletcher–Goldfarb-Shanno (BFGS) matrix in the Frobenius norm. Moreover, the resulting direction is descent independent of any line search condition. We established the global convergence of the proposed algorithm under some appropriate assumptions. In addition, numerical experiments on some benchmark test problems are reported in order to show the efficiency of the proposed algorithm.

1 Introduction

Our concern is a problem of finding a point x ∈ Ω such that
F ( x ) = 0 , ()
where Ω is nonempty, closed, and convex subset of ℝ n , the function F is a continuous function from ℝ n to ℝ n . If F is monotone, then (1) is called a convex constraints nonlinear monotone equation. Methods for solving (1) were presented in many literature. Among the widely used are derivative-free algorithms (see e.g., References 1-8 and references therein). Moreover, quasi-Newton methods are also effective methods for solving (1).9

Recently, Gao et al.10 proposed an adaptive three-term derivative-free algorithms to solve (1). Following the approaches in References 11-13, they proposed two parameters based on the modified Liu-Storey (LS) conjugate gradient direction. The two parameters were obtained by minimizing the distance between the self-scaling memory-less BFGS update and the relative matrix corresponding to the proposed search direction.

Motivated by the work of Gao et al., we propose two positive parameters similar to that of Birgin and Martínez14 spectral parameter for solving (1). Under appropriate assumptions, we establish the global convergence of the algorithm. Finally, we applied the algorithm to find solutions of nonlinear monotone operator equations with convex constraints.

The remaining part of the manuscript is as follows. Section 2 described the two algorithms and their global convergence is proved in Section 3. Some numerical experiments were reported in Section 4. Finally, Section 5 concludes the paper. Unless otherwise stated, the function F is assumed to be monotone, that is, for all x , y ∈ ℝ n
( F ( x ) − F ( y ) ) T ( x − y ) ≥ 0 .
Furthermore, the symbol ‖ · ‖ stands for Euclidean norm on ℝ n and F(xk) is abbreviated to Fk.

2 Algorithm

The iterative formula of a derivative-free method for solving (1) is given by
x k + 1 = x k + α k d k , k = 0 , 1 , … ()
where α k > 0 is a scalar and dk the direction given by
d k = − F 0 , if k = 0 − θ k F k + β k s k − 1 , if k = 1 , 2 , … ()
where θ k and β k are parameters. If θ k = 1 we have the classical derivative-free direction depending on the value of the parameter β k , for example, the LS, Polak-Ribi è re-Polyak (PRP), and Hestenes-Stiefel (HS) parameters are, respectively, given by;
β k LS = F k T y k − 1 − F k − 1 T d k − 1 , β k PRP = F k T y k − 1 ‖ F k − 1 ‖ 2 , β k HS = F k T y k − 1 d k − 1 T y k − 1 , y k − 1 = F k − F k − 1 .
If θ k is any positive real number different from 1, the search direction becomes the spectral conjugate gradient direction initially introduced by Birgin and Martínez14 for unconstrained optimization problems.
In this paper, we consider β k based on the Birgin and Martínez-scaled parameter and the corresponding search direction as:
β k = θ k ū k − 1 T F k ū k − 1 T s k − 1 − t k F k T s k − 1 ū k − 1 T s k − 1 , ()
d k = − θ k F k + β k s k − 1 − θ k F k T s k − 1 ū k − 1 T s k − 1 ū k − 1 , k = 1 , 2 , … , ()
with s k − 1 = x k − x k − 1 , ū k − 1 = F k − F k − 1 + r s k − 1 , r > 0. The scaling parameter tk ≥ 0 can be chosen as follows.
By substituting Equation (4) into (5) and performing some simple algebraic simplifications, the proposed search direction can be written as:
d k = − Q k F k , ()
where
Q k = θ k I − θ k s k − 1 ū k − 1 T − ū k − 1 s k − 1 T ū k − 1 T s k − 1 + t k s k − 1 s k − 1 T ū k − 1 T s k − 1 . ()
Consider the self-scaling memory-less BFGS update matrix
H k = θ k I − θ k s k − 1 ū k − 1 T + ū k − 1 s k − 1 T ū k − 1 T s k − 1 + 1 + θ k ‖ ū k − 1 ‖ 2 ū k − 1 T s k − 1 s k − 1 s k − 1 T ū k − 1 T s k − 1 . ()
Based on the similarities between the the matrices Qk and Hk in (7) and (8), respectively, we propose computing the scaling parameter tk as a solution of the following minimization problem:
min t k > 0 ‖ E k ‖ F 2 = min t k > 0 trace ( E k T E k ) , ()
where Ek = Qk − Hk and ‖ · ‖F is the Frobenius norm. Now, from Equations (7) and (8) we have
E k = t k s k − 1 s k − 1 T ū k − 1 T s k − 1 + A k , ()
where
A k = 2 θ k ū k − 1 s k − 1 T ū k − 1 T s k − 1 − 1 + θ k ‖ ū k − 1 ‖ 2 ū k − 1 T s k − 1 s k − 1 s k − 1 T ū k − 1 T s k − 1 .
So that,
E k E k T = t k 2 ( s k − 1 s k − 1 T ) 2 ( ū k − 1 T s k − 1 ) 2 + t k s k − 1 s k − 1 T ū k − 1 T s k − 1 A k + t k A k T s k − 1 s k − 1 T ū k − 1 T s k − 1 + A k A k T .
Therefore,
trace ( E k E k T ) = t k 2 ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 2 + 4 t k θ k ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 − 2 t k ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 2 − 2 t k θ k ‖ ū k − 1 ‖ 2 ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 3 .
Differentiating the above equation with respect to tk and equating to zero, we have
2 t k ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 2 + 4 θ k ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 − 2 ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 2 − 2 θ k ‖ ū k − 1 ‖ 2 ‖ s k − 1 ‖ 4 ( ū k − 1 T s k − 1 ) 3 = 0 ,
which implies
t k = 1 + θ k ‖ ū k − 1 ‖ 2 ū k − 1 T s k − 1 − 2 ū k − 1 T s k − 1 ‖ s k − 1 ‖ 2 . ()
From the definition of ū k − 1 , monotonicity of F and r > 0, we have
ū k − 1 T s k − 1 = ( F k − F k − 1 ) T s k − 1 + r ‖ s k − 1 ‖ 2 ≥ r ‖ s k − 1 ‖ 2 > 0 . ()
Also, by Cauchy–Schwartz inequality, (12) and ‖sk−1‖ ≠ 0, we get
‖ ū k − 1 ‖ 2 ū k − 1 T s k − 1 ≥ ū k − 1 T s k − 1 ‖ s k − 1 ‖ 2 . ()
Now if θ k = ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 , then
t k B B 1 = ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 ( ū k − 1 T s k − 1 ) 2 − 1 , ()
and if θ k = ū k − 1 T s k − 1 ‖ ū k − 1 ‖ 2 , then
t k B B 2 = 2 1 − ( ū k − 1 T s k − 1 ) 2 ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 . ()
From (13), we have that
‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 ( ū k − 1 T s k − 1 ) 2 ≥ 1 ,
and
( ū k − 1 T s k − 1 ) 2 ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 ≤ 1 .
Therefore in both Equations (14) and (15), t k B B 1 , t k B B 2 ≥ 0 ∀ k ≥ 1 .

Based on the above, we now present present our algorithm which combines the projection technique of Solodov and Svaiter15 with the derivative-free direction given in Equation (5).

Algorithm 1. Derivative-free algorithm (DFAP)

cmm41176-gra-1000-b

Remark 1.The projection operator P Ω in Algorithm 1 is defined for all x ∈ ℝ n by

P Ω ( x ) = arg min { ‖ x − y ‖ : y ∈ Ω } .

3 Convergence result

In this section, we will begin with some assumptions and Lemmas that will be useful in establishing the main theorem.

Throughout we assume the followings
  • (G1) The solution set Ω ′ of (1), is nonempty.
  • (G2) The function F is Lipschitz continuous, that is, there exists a positive constant L such that for all x , y ∈ ℝ n
    ‖ F ( x ) − F ( y ) ‖ ≤ L ‖ x − y ‖ .

Lemma 1.The search direction defined by (5) satisfies the following inequality

F k T d k ≤ − c ‖ F k ‖ 2 .

Proof.If k = 0,

F k T d k = − ‖ F k ‖ 2 .
If k ≥ 1,
F k T d k = − θ k ‖ F k ‖ 2 + θ k ( ū k − 1 T F k ) ( F k T s k − 1 ) ū k − 1 T s k − 1 − t k ( F k T s k − 1 ) ( F k T s k − 1 ) ū k − 1 T s k − 1 − θ k ( F k T s k − 1 ) ( F k T ū k − 1 ) ū k − 1 T s k − 1 = − θ k ‖ F k ‖ 2 − t k ( F k T s k − 1 ) 2 ū k − 1 T s k − 1 ≤ − θ k ‖ F k ‖ 2 .

Now if θ k = ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 , then

F k T d k ≤ − ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 ‖ F k ‖ 2 ≤ − ‖ s k − 1 ‖ 2 ( L + r ) ‖ s k − 1 ‖ 2 ‖ F k ‖ 2 = − 1 L + r ‖ F k ‖ 2 .

Also if θ k = ū k − 1 T s k − 1 ‖ ū k − 1 ‖ 2 , then

F k T d k ≤ − r ( L + r ) 2 ‖ F k ‖ 2 .
Letting c = max 1 , 1 L + r , r ( L + r ) 2 , then
F k T d k ≤ − c ‖ F k ‖ 2 . ()

Lemma 2.Let Assumptions (G1) and (G2) be fulfilled. If the sequence {dk} is defined by (4) and (5), then there exists M > 0 such that

‖ d k ‖ ≤ M ‖ F k ‖ . ()

Proof.

‖ d k ‖ = − θ k F k + θ k ū k − 1 T F k ū k − 1 T s k − 1 s k − 1 − t k F k T s k − 1 ū k − 1 T s k − 1 s k − 1 − θ k F k T s k − 1 ū k − 1 T s k − 1 ū k − 1 ≤ θ k ‖ F k ‖ + θ k ‖ ū k − 1 ‖ ‖ F k ‖ r ‖ s k − 1 ‖ 2 ‖ s k − 1 ‖ + t k ‖ F k ‖ ‖ s k − 1 ‖ r ‖ s k − 1 ‖ 2 ‖ s k − 1 ‖ + θ k ‖ F k ‖ ‖ s k − 1 ‖ r ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ ≤ θ k ‖ F k ‖ + θ k ( L + r ) ‖ s k − 1 ‖ ‖ F k ‖ r ‖ s k − 1 ‖ 2 ‖ s k − 1 ‖ + t k ‖ F k ‖ ‖ s k − 1 ‖ r ‖ s k − 1 ‖ 2 ‖ s k − 1 ‖ + θ k ‖ F k ‖ ‖ s k − 1 ‖ r ‖ s k − 1 ‖ 2 ( L + r ) ‖ s k − 1 ‖ = θ k ‖ F k ‖ + θ k ( L + r ) ‖ F k ‖ r + t k ‖ F k ‖ r + θ k ( L + r ) ‖ F k ‖ r = θ k r + 2 ( L + r ) r ‖ F k ‖ + t k ‖ F k ‖ r . ()

If θ k = ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 , t k = t k B B 1 , then

‖ d k ‖ ≤ ‖ s k − 1 ‖ 2 ū k − 1 T s k − 1 r + 2 ( L + r ) r ‖ F k ‖ + ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 ( ū k − 1 T s k − 1 ) 2 − 1 ‖ F k ‖ r ≤ ‖ s k − 1 ‖ 2 r ‖ s k − 1 ‖ 2 r + 2 ( L + r ) r ‖ F k ‖ + ( L + r ) 2 ‖ s k − 1 ‖ 4 r 2 ‖ s k − 1 ‖ 4 ‖ F k ‖ r = 1 r 2 r 2 + 2 r ( L + r ) + ( L + r ) 2 r ‖ F k ‖ = 1 r 3 ( 2 r + L ) 2 ‖ F k ‖ . ()

In a similar way if θ k = ū k − 1 T s k − 1 ‖ ū k − 1 ‖ 2 , t k = t k B B 2 , then

‖ d k ‖ ≤ ū k − 1 T s k − 1 ‖ ū k − 1 ‖ 2 r + 2 ( L + r ) r ‖ F k ‖ + 2 1 − ( ū k − 1 T s k − 1 ) 2 ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 ‖ F k ‖ r ≤ ( L + r ) ‖ s k − 1 ‖ 2 ‖ ū k − 1 ‖ 2 r + 2 ( L + r ) r ‖ F k ‖ + 2 r ‖ F k ‖ ≤ ( L + r ) ‖ s k − 1 ‖ 2 r 2 ‖ s k − 1 ‖ 2 r + 2 ( L + r ) r ‖ F k ‖ + 2 r ‖ F k ‖ = ( L + r ) r 2 r + 2 ( L + r ) r ‖ F k ‖ + 2 r ‖ F k ‖ = ( L + r ) ( r + 2 ( L + r ) ) + 2 r 2 r 3 ‖ F k ‖ . ()

Letting M = min 1 r 3 ( 2 r + L ) 2 , 1 r 3 ( L + r ) ( r + 2 ( L + r ) ) + 2 r 2 , then

‖ d k ‖ ≤ M ‖ F k ‖ .

Lemma 3.Let Assumption (G2) be fulfilled. Then for any ρ , c , L , σ > 0 we have

α k ≥ min 1 , ρ c ‖ F k ‖ 2 ( L + σ ) ‖ d k ‖ 2 . ()

Proof.Suppose α k ≠ 1 in the line search, then ρ − 1 α k does not satisfy (17). That is

− F ( x k + ρ − 1 α k d k ) T d k < σ ρ − 1 α k ‖ d k ‖ 2 .
Using the above inequality and Lemma 1, we have
c ‖ F k ‖ 2 ≤ − F k T d k = ( F ( x k + ρ − 1 α k d k ) T d k − F k T d k ) − F ( x k + ρ − 1 α k d k ) T d k ≤ L ρ − 1 α k ‖ d k ‖ 2 + σ ρ − 1 α k ‖ d k ‖ 2 .

Hence, we have

α k ≥ min 1 , ρ c ‖ F k ‖ 2 ( L + σ ) ‖ d k ‖ 2 .

Lemma 4.16 Let Assumptions (G1) and (G2) be fulfilled. If { η k } and {xk} are generated by (16) and (18) in Algorithm 1, then

lim k → ∞ ‖ x k − η k ‖ = 0 . ()

Remark 2.Equation (25) and definition of η k implies that

lim k → ∞ α k ‖ d k ‖ = 0 . ()

Theorem 1.Let the sequence {xk} be generated by (18) in Algorithm 1. Then

lim inf k → ∞ ‖ F k ‖ = 0 . ()

Proof.By Cauchy–Schwartz inequality and Lemma 1 we have

‖ d k ‖ ≥ c ‖ F k ‖ .
From (20), (24), and (26)
α k ≥ min 1 , ρ c ( L + σ ) M 2 > 0 .
It holds that
lim k → ∞ ‖ d k ‖ = 0 ,
then
0 = lim inf k → ∞ ‖ d k ‖ ≥ c lim inf k → ∞ ‖ F k ‖ ,
this implies (27).

4 Numerical examples

In this section, we report some numerical results to show the efficiency of the proposed Algorithm 1 (DFAP). For simplicity, we represent Algorithm 1 by DFAP. Algorithm 1 with t k = t k B B 1 and Algorithm 1 with t k = t k B B 2 are named as DFAP1 and DFAP2, respectively. Based on (4) and (5) the proposed algorithm has similar structure with MHSP method proposed by Awwal et al.17 and algorithm 2.1b proposed by Gao et al.10 We compare the numerical performances of DFAP1, DFAP2, MHSP and algorithm 2.1b on nonlinear monotone operator equations. All experiments were done using the MATLAB software.

We adopt the same line search implementation for both DFAP1, DFAP2, MHSP, and algorithm 2.1b, with the following parameters specifications. For DFAP algorithm, ρ = 0 . 6 , r = 0.1, μ = 1 . 8 , σ = 0 . 0001 . For MHSP algorithm and Algorithm 2.1b, all parameters are choosen as in References 17 and 10, respectively. The stopping condition used for the algorithms is ‖Fk‖<10−6. We considered seven problems with dimensions ranging from 5000 to 100,000 and eight initial points as follows: x1 = (1, 1, …, 1)T, x2 = (0.5, 0.5, … , 0.5)T, x3 = (1, 1/2, … , 1/n)T, x4 = (1/n, 2/n, … , 1)T, x5 = (1/3, 1/32, … , 1/3n)T, x6 = (1/4, 1/2, … , 1/4, 1/2)T, x7 = (10, 10, … , 10)T, x8 = rand(0, 1).

We use the popular Dolan and Moré performance profile18 to assess the algorithms. Figures 1, 2, and 3 contain the plot of P ( τ ) against τ where τ represent the best ratio of number of iterations, function evaluations and CPU time, respectively. The numerical results are tabulated in Tables A1, A2, A3, A4, A5, A6, and A7 (see Appendix).

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Performance profiles based on number of iterations metric
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Performance profiles based on number of function evaluations metric
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Performance profiles based on CPU time metric
Below are the test problems considered for the implementation of the algorithms where F = (f1, f2, … , fn)T. Problem 119
f i ( x ) = e 2 x i + 3 sin x i cos x i − 1 , i = 1 , 2 , … , n , Ω = ℝ + n .
Problem 2 Discrete boundary value problem20
f i ( x ) = 2 x i − x i − 1 − x i + 1 + h 2 2 ( x i + t i + 1 ) 3 , for i = 1 , 2 , 3 , . . . , n , where h = 1 n + 1 , t i = i h , and x 0 = x n + 1 = 0 , Ω = ℝ + n .
Problem 3 Modified Tridiagonal exponential function21
f 1 ( x ) = x 1 − e cos 1 2 x 1 + x 2 f i ( x ) = x i − e cos 1 i x i − 1 + x i + x i + 1 , i = 2 , … , n − 1 , f n ( x ) = x n − e cos 1 n x n − 1 + x n , Ω = ℝ + n .
Problem 4 problem 3 in Reference 19
f 1 ( x ) = 2 x 1 + sin x 1 − 1 , f i ( x ) = 2 x i − 1 + 2 x i + sin x i − 1 , f n ( x ) = 2 x n + sin x n − 1 , Ω = ℝ + n .
Problem 5 Exponential function22
f 1 ( x ) = e x 1 − 1 , f i ( x ) = e x i + x i − 1 , for i = 2 , 3 , … , n , Ω = ℝ + n .
Problem 6 Modified logarithmic function22
f i ( x i ) = log ( x i + 1 ) − x i n , i = 1 , 2 , … , n , Ω = ℝ + n .
Problem 7 Nonsmooth function I23
f i ( x ) = 2 x i − sin | x i | , i = 1 , 2 , … , n , Ω = x ∈ ℝ n : ∑ i = 1 n x i ≤ n , x i ≥ 0 , i = 1 , 2 , … , n .

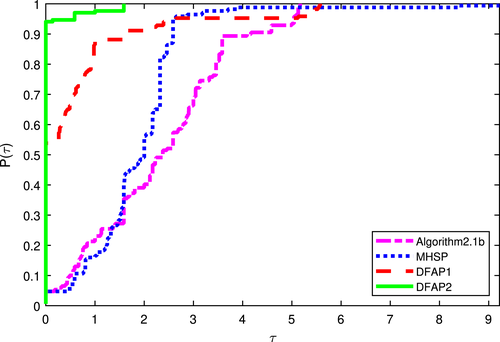
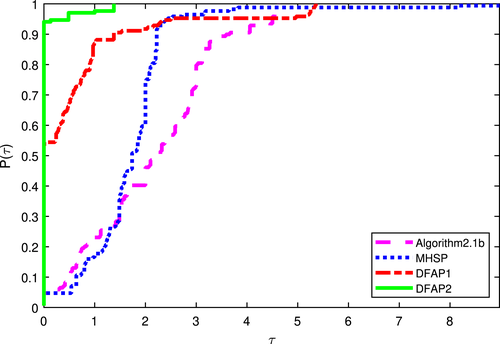
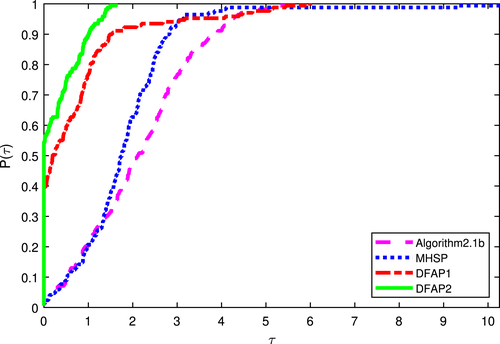
Figures 1, 2, and 3 show that DFAP1 and DFAP2 solvers outperforms the MHSP and algorithm 2.1b solvers. Figure 1 display the performance of the algorithms with respect to the number of iterations metric. From Figure 1 it can be easily observed that DFAP1 and DFAP2 solve at least 55% and 90% of the problems with least number of iterations, respectively. Figure 2 shows DFAP2 solves more than 90% of the problems with the fewer number of function evaluations. From Figure 3, DFAP2 algorithm outperform DFAP1, MHSP, and algorithm 2.1b, which indicates that our approach is very efficient in solving nonlinear monotone operator equations.

5 Conclusions

We proposed two derivative-free projection algorithms (DFAP) as an alternative approach with high efficiency to solve nonlinear monotone operator equations. Also, a comparison between the results of applying the proposed algorithms and other similar algorithms in the literature was shown. The results showed that the DFAP algorithms are very effective to solve nonlinear monotone operator equations. This good performance of DFAP algorithms may be due to the closeness of the relative matrix corresponding to its search direction and memory-less BFGS update matrix. Finally, further research should be performed to solve other kinds of problems like signal restoration and image deblurring, among others.

Acknowledgments

The first author acknowledge with thanks, the Department of Mathematics and Applied Mathematics at the Sefako Makgatho Health Sciences University.

    Conflict of Interest

    The authors declare no potential conflict of interest.

    APPENDIX A

    TABLE A1. Numerical results for DFAP1, DFAP2, MHSP, and algorithm 2.1b for Problem 1 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 1 3 0.00944 0.00E+00 1 3 0.01066 0.00E+00 1 3 0.013602 0.00E+00 1 3 0.025573 0.00E+00
    x 0 2 1 3 0.005771 0.00E+00 1 3 0.024505 0.00E+00 1 3 0.012575 0.00E+00 1 3 0.009563 0.00E+00
    x 0 3 12 26 0.068913 3.81E-07 8 18 0.047103 5.46E-07 2 5 0.017498 0.00E+00 3 7 0.034469 0.00E+00
    x 0 4 13 28 0.056851 6.19E-07 17 36 0.063313 7.69E-09 131 263 1.1509 9.07E-07 3 7 0.018053 0.00E+00
    x 0 5 8 18 0.069306 7.62E-07 4 10 0.0462 1.68E-08 1 3 0.008758 2.22E-16 1 3 0.022907 2.22E-16
    x 0 6 11 24 0.065081 7.18E-07 6 14 0.047362 2.50E-08 1 3 0.01231 0.00E+00 1 3 0.011147 0.00E+00
    x 0 7 13 28 0.10643 5.92E-07 18 38 0.1167 1.92E-08 128 257 0.69827 9.21E-07 3 7 0.016064 0.00E+00
    10,000 x 0 1 1 3 0.012447 0.00E+00 1 3 0.023016 0.00E+00 1 3 0.020907 0.00E+00 1 3 0.01537 0.00E+00
    x 0 2 1 3 0.038624 0.00E+00 1 3 0.011714 0.00E+00 1 3 0.012229 0.00E+00 1 3 0.009078 0.00E+00
    x 0 3 12 26 0.093608 3.82E-07 8 18 0.10187 6.35E-07 2 5 0.014325 0.00E+00 3 7 0.024873 0.00E+00
    x 0 4 13 28 0.087556 8.73E-07 15 32 0.24121 1.94E-08 133 267 0.79299 9.51E-07 3 7 0.037647 0.00E+00
    x 0 5 8 18 0.12638 7.62E-07 4 10 0.047969 1.68E-08 1 3 0.023527 2.22E-16 1 3 0.012792 2.22E-16
    x 0 6 12 26 0.094418 2.03E-07 6 14 0.081283 3.53E-08 1 3 0.016391 0.00E+00 1 3 0.02294 0.00E+00
    x 0 7 13 28 0.16202 8.56E-07 14 30 0.18264 3.28E-09 133 267 1.109 9.91E-07 3 7 0.042715 0.00E+00
    50,000 x 0 1 1 3 0.046935 0.00E+00 1 3 0.067238 0.00E+00 1 3 0.10584 0.00E+00 1 3 0.09484 0.00E+00
    x 0 2 1 3 0.065212 0.00E+00 1 3 0.039154 0.00E+00 1 3 0.036445 0.00E+00 1 3 0.078765 0.00E+00
    x 0 3 12 26 0.58108 3.82E-07 9 20 0.4897 7.54E-08 2 5 0.15212 0.00E+00 3 7 0.16398 0.00E+00
    x 0 4 14 30 0.5935 3.90E-07 16 33 0.70846 0.00E+00 139 279 3.9727 8.68E-07 3 7 0.11689 0.00E+00
    x 0 5 8 18 0.39519 7.62E-07 4 10 0.11071 1.68E-08 1 3 0.082504 2.22E-16 1 3 0.056377 2.22E-16
    x 0 6 12 26 0.43972 4.54E-07 6 14 0.14471 7.89E-08 1 3 0.057092 0.00E+00 1 3 0.085838 0.00E+00
    x 0 7 14 30 0.74741 3.89E-07 18 38 0.53167 2.12E-09 140 281 3.4036 9.74E-07 4 9 0.20161 0.00E+00
    100,000 x 0 1 1 3 0.1336 0.00E+00 1 3 0.15289 0.00E+00 1 3 0.081728 0.00E+00 1 3 0.21135 0.00E+00
    x 0 2 1 3 0.094223 0.00E+00 1 3 0.1204 0.00E+00 1 3 0.1126 0.00E+00 1 3 0.16619 0.00E+00
    x 0 3 12 26 0.77922 3.82E-07 12 26 0.7045 1.58E-08 2 5 0.15634 0.00E+00 3 7 0.24211 0.00E+00
    x 0 4 14 30 0.84163 5.52E-07 1000 2000 145.4787 NaN 141 283 8.0814 9.11E-07 3 7 0.22674 0.00E+00
    x 0 5 8 18 0.69774 7.62E-07 4 10 0.36086 1.68E-08 1 3 0.20281 2.22E-16 1 3 0.11986 2.22E-16
    x 0 6 12 26 1.3034 6.42E-07 6 14 0.63727 1.12E-07 1 3 0.11005 0.00E+00 1 3 0.14494 0.00E+00
    x 0 7 14 30 0.70666 5.48E-07 22 46 1.6593 4.86E-08 143 287 8.4654 9.33E-07 3 7 0.38032 0.00E+00
    TABLE A2. Numerical results for DFAP1, DFAP2, MHSP, and algorithm 2.1b for Problem 2 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 258 517 2.1415 9.86E-07 100 201 1.2825 9.30E-07 67 135 0.50093 9.05E-07 35 71 0.20563 9.56E-07
    x 0 2 273 547 2.1893 9.99E-07 108 217 0.83182 9.74E-07 66 133 0.82226 8.67E-07 33 67 0.45219 9.71E-07
    x 0 3 85 171 0.51765 8.76E-07 79 159 1.0286 9.98E-07 49 99 0.43469 9.04E-07 33 67 0.36061 8.69E-07
    x 0 4 200 401 1.8721 9.92E-07 172 345 1.1797 9.84E-07 33 67 0.39644 9.40E-07 19 39 0.21633 8.00E-07
    x 0 5 93 187 0.65113 9.82E-07 75 151 0.43872 9.00E-07 57 115 0.43262 8.05E-07 43 87 0.43944 6.82E-07
    x 0 6 257 515 2.8343 9.86E-07 102 205 1.278 9.81E-07 65 131 0.97133 9.44E-07 33 67 0.47048 9.71E-07
    x 0 7 263 527 1.4476 9.98E-07 155 311 1.0643 9.92E-07 41 83 0.2255 8.47E-07 41 83 0.28319 8.63E-07
    10,000 x 0 1 253 507 2.4583 9.23E-07 100 201 0.96384 6.95E-07 69 139 0.7629 5.19E-07 35 71 0.66753 8.59E-07
    x 0 2 247 495 3.5486 7.31E-07 98 197 0.95199 9.30E-07 65 131 1.4066 9.93E-07 33 67 0.51191 8.78E-07
    x 0 3 85 171 1.8177 9.41E-07 79 159 1.4193 8.62E-07 51 103 1.115 8.96E-07 27 55 0.54587 8.18E-07
    x 0 4 138 277 2.1866 7.39E-07 158 317 2.5619 9.03E-07 30 61 0.81474 7.55E-07 17 35 0.46101 6.70E-07
    x 0 5 94 189 2.0818 8.84E-07 75 151 1.4116 9.42E-07 56 113 1.5979 7.48E-07 43 87 0.92328 7.34E-07
    x 0 6 247 495 3.9121 7.02E-07 99 199 1.9579 7.34E-07 65 131 1.4965 7.95E-07 33 67 0.79373 8.78E-07
    x 0 7 233 467 3.4051 6.80E-07 132 265 2.8016 8.12E-07 60 121 1.4325 7.64E-07 36 73 0.72885 8.56E-07
    50,000 x 0 1 251 504 12.3602 7.86E-07 101 203 5.0709 8.61E-07 66 133 4.5452 8.66E-07 35 71 2.5754 8.44E-07
    x 0 2 239 480 11.894 9.62E-07 100 201 5.8554 7.08E-07 64 129 3.3901 6.12E-07 33 67 1.5727 8.65E-07
    x 0 3 85 171 3.6672 9.57E-07 76 153 3.426 9.93E-07 46 93 3.7415 8.16E-07 32 65 1.3452 8.91E-07
    x 0 4 52 105 2.3227 8.23E-07 156 313 7.3238 8.08E-07 25 51 2.5151 7.51E-07 12 25 1.225 8.59E-07
    x 0 5 94 189 5.5155 9.01E-07 75 151 3.428 9.54E-07 56 113 3.6026 7.26E-07 43 87 3.1628 7.46E-07
    x 0 6 240 482 10.4648 9.94E-07 100 201 6.3418 9.12E-07 65 131 3.4078 8.15E-07 33 67 1.7099 8.65E-07
    x 0 7 244 489 12.4358 8.77E-07 124 249 7.1611 6.54E-07 50 101 2.3182 9.74E-07 41 83 2.4979 7.02E-07
    100,000 x 0 1 237 476 23.8027 9.92E-07 102 205 11.2154 8.27E-07 66 133 9.1363 9.70E-07 35 71 4.8884 8.44E-07
    x 0 2 229 460 22.8065 8.70E-07 101 203 10.8456 6.80E-07 65 131 8.0762 7.84E-07 33 67 3.0973 8.65E-07
    x 0 3 85 171 9.0708 9.58E-07 80 161 9.0271 9.07E-07 46 93 6.1977 9.51E-07 32 65 4.1031 8.86E-07
    x 0 4 52 105 6.6891 8.85E-07 162 325 13.9044 8.30E-07 21 43 3.7299 7.15E-07 11 23 1.0663 7.49E-07
    x 0 5 94 189 10.4225 9.01E-07 75 151 8.7783 9.54E-07 56 113 7.2565 7.26E-07 43 87 3.5007 7.46E-07
    x 0 6 228 458 23.0091 8.87E-07 100 201 9.5313 7.65E-07 65 131 8.8313 8.21E-07 33 67 3.8494 8.65E-07
    x 0 7 237 475 22.0842 7.97E-07 125 251 12.531 6.62E-07 71 143 8.306 9.66E-07 43 87 5.0248 7.55E-07
    TABLE A3. Numerical results for DFAP1, DFAP2, MHSP, and algorithm 2.1b for Problem 3 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    DIMENSION x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 24 50 0.23553 4.92E-07 34 70 0.18473 3.02E-07 25 52 0.13569 4.51E-07 20 42 0.11044 4.18E-07
    x 0 2 25 52 0.0891 1.94E-07 39 80 0.25274 4.43E-07 24 50 0.10145 9.91E-07 14 30 0.13913 6.30E-07
    x 0 3 25 52 0.20062 7.93E-07 39 80 0.28804 3.21E-07 26 54 0.096348 4.29E-07 17 36 0.099097 6.61E-07
    x 0 4 24 50 0.20379 4.47E-07 40 82 0.17016 3.60E-07 25 52 0.070165 6.31E-07 16 34 0.12113 6.13E-07
    x 0 5 26 54 0.20451 3.51E-07 38 78 0.46804 3.83E-07 29 60 0.28106 2.23E-07 16 34 0.13864 3.35E-07
    x 0 6 24 50 0.13091 9.75E-07 38 78 0.22335 6.29E-07 25 52 0.19771 8.51E-07 15 32 0.14371 5.80E-07
    x 0 7 25 52 0.13654 1.59E-07 36 74 0.29349 3.48E-07 24 49 0.10955 8.57E-07 20 42 0.14104 3.79E-07
    10,000 x 0 1 25 52 0.30433 2.90E-07 35 72 0.57578 7.03E-07 26 54 0.22293 7.24E-07 15 31 0.20325 5.27E-07
    x 0 2 25 52 0.284 7.14E-07 35 72 0.4544 8.49E-07 25 52 0.15537 6.41E-07 17 36 0.2074 4.94E-07
    x 0 3 24 50 0.19174 7.08E-07 36 74 0.53601 8.77E-07 17 36 0.095393 7.83E-07 14 30 0.11947 7.99E-07
    x 0 4 26 54 0.32735 3.90E-07 40 82 0.37785 5.27E-07 23 48 0.10059 2.09E-07 14 29 0.23604 6.21E-07
    x 0 5 25 52 0.38222 9.32E-07 33 68 0.29752 4.59E-07 28 58 0.46259 7.99E-07 14 29 0.15502 9.97E-07
    x 0 6 26 54 0.42566 2.99E-07 38 78 0.47069 4.68E-07 20 42 0.1489 9.47E-07 19 40 0.27596 9.69E-07
    x 0 7 25 52 0.2422 3.47E-07 38 78 0.24069 1.70E-07 33 68 0.32953 4.54E-07 17 36 0.17654 9.98E-07
    50,000 x 0 1 27 56 0.95739 4.31E-07 44 90 2.0587 7.26E-07 23 48 0.89156 4.96E-07 18 38 0.63034 7.06E-07
    x 0 2 26 54 0.70218 5.45E-07 40 82 1.7878 2.17E-07 28 58 0.77756 2.56E-07 23 47 1.1478 6.32E-07
    x 0 3 27 56 0.64148 6.57E-07 71 144 1.6418 3.82E-07 28 58 1.4334 3.50E-07 20 42 0.91539 6.47E-07
    x 0 4 27 56 1.4254 4.93E-07 43 88 1.0665 1.23E-07 21 44 1.1954 2.39E-07 17 36 0.58036 8.35E-07
    x 0 5 27 56 1.3624 2.62E-07 71 144 2.9918 5.40E-08 21 44 0.75415 6.55E-07 16 34 0.5366 3.57E-07
    x 0 6 27 56 0.94009 7.33E-07 38 78 1.6671 9.68E-07 23 48 0.69802 9.74E-07 16 34 0.51258 7.05E-07
    x 0 7 25 52 1.3223 8.06E-07 39 80 2.1071 6.68E-07 25 52 1.0267 4.91E-07 19 40 0.92896 2.68E-07
    100,000 x 0 1 27 56 2.3984 9.01E-07 47 96 3.9928 7.72E-07 26 54 1.3504 7.89E-07 17 35 1.6678 5.87E-07
    x 0 2 28 58 2.4352 5.19E-07 76 154 5.0567 2.06E-07 24 50 1.8427 2.59E-07 17 36 1.1614 4.04E-07
    x 0 3 27 56 2.2822 4.36E-07 93 188 5.8096 6.74E-07 28 58 2.5609 3.37E-07 20 41 1.0643 5.30E-07
    x 0 4 27 56 2.5654 3.74E-07 80 162 3.6568 9.62E-07 24 50 2.1334 3.93E-07 16 34 1.7242 8.36E-07
    x 0 5 27 56 2.8904 9.27E-07 90 182 5.3681 2.24E-07 26 54 2.2362 2.02E-07 17 36 1.6574 6.15E-07
    x 0 6 28 58 2.6732 1.38E-07 82 166 5.2949 9.39E-07 27 56 1.9129 5.77E-07 20 41 1.9361 7.49E-07
    x 0 7 27 56 2.5301 3.26E-07 79 160 5.153 1.58E-07 20 42 1.5302 8.21E-07 22 46 1.6963 7.53E-07
    TABLE A4. Numerical results for DFAP1, DFAP2, MHSP, and Algorithm 2.1b for Problem 4 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    1000 x 0 1 17 36 0.068691 7.43E-07 31 64 0.075828 7.36E-07 862 1725 1.6982 9.99E-07 32 66 0.077646 4.84E-07
    x 0 2 17 36 0.044199 7.65E-07 28 58 0.050422 8.71E-07 877 1755 1.9618 9.97E-07 32 66 0.051791 8.07E-07
    x 0 3 18 38 0.035713 6.96E-07 37 76 0.06306 5.96E-07 1000 2000 1.8068 2.03E-06 32 66 0.042845 6.59E-07
    x 0 4 19 40 0.031731 7.75E-07 23 48 0.053245 6.84E-07 1000 2000 2.1174 1.50E-06 35 72 0.070273 8.16E-07
    x 0 5 17 36 0.045212 8.29E-07 30 62 0.043741 7.76E-07 894 1789 2.1034 9.97E-07 28 58 0.057748 7.46E-07
    x 0 6 91 184 0.28031 9.22E-07 26 54 0.058876 5.27E-07 1000 2000 2.6253 1.04E-02 49 100 0.087697 9.33E-07
    x 0 7 35 72 0.053541 8.92E-07 38 78 0.054917 9.94E-07 1000 2000 2.3352 9.45E-06 38 78 0.072471 5.08E-07
    x 0 8 65 132 0.077565 8.49E-07 34 70 0.036823 4.68E-07 1000 2000 2.3879 1.12E-06 84 170 0.11221 9.28E-07
    5000 x 0 1 17 36 0.1269 8.20E-07 30 62 0.071835 1.00E-06 750 1501 2.9622 9.96E-07 39 80 0.12827 9.28E-07
    x 0 2 17 36 0.072157 6.02E-07 36 74 0.21312 5.80E-07 748 1497 3.6137 9.97E-07 29 60 0.22499 9.99E-07
    x 0 3 18 38 0.12543 4.94E-07 29 60 0.12578 9.76E-07 1000 2000 3.2029 2.21E-06 38 78 0.25607 9.57E-07
    x 0 4 18 38 0.13771 6.57E-07 29 60 0.1399 6.35E-07 1000 2000 5.237 1.15E-06 30 62 0.11535 6.70E-07
    x 0 5 17 36 0.12013 5.68E-07 34 70 0.18052 8.87E-07 766 1533 3.9603 9.99E-07 37 75 0.15279 8.47E-07
    x 0 6 97 196 0.54992 9.41E-07 28 58 0.1632 6.14E-07 1000 2000 5.0308 9.68E-03 50 102 0.15133 9.13E-07
    x 0 7 30 62 0.1321 8.41E-07 38 78 0.1991 7.24E-07 1000 2000 2.9517 1.03E-05 50 102 0.27276 9.31E-07
    x 0 8 69 140 0.21788 9.49E-07 31 64 0.098667 5.22E-07 1000 2000 4.6784 3.02E-05 48 98 0.21921 9.30E-07
    10,000 x 0 1 17 36 0.21425 8.91E-07 34 70 0.45362 9.18E-07 689 1379 3.8782 9.95E-07 31 64 0.25319 9.11E-07
    x 0 2 17 36 0.23345 5.90E-07 29 60 0.27139 7.10E-07 702 1405 5.178 9.96E-07 34 70 0.25777 5.97E-07
    x 0 3 17 36 0.18332 9.96E-07 29 60 0.1802 4.82E-07 1000 2000 7.9777 1.65E-06 35 72 0.38096 8.83E-07
    x 0 4 18 38 0.10674 5.53E-07 28 58 0.15819 3.88E-07 1000 2000 7.4203 9.95E-07 36 74 0.35294 7.40E-07
    x 0 5 17 36 0.18176 5.26E-07 31 64 0.27851 9.33E-07 717 1435 4.9122 9.96E-07 41 84 0.32563 9.97E-07
    x 0 6 101 204 0.53423 8.97E-07 25 52 0.1423 4.94E-07 1000 2000 7.4041 8.71E-03 122 246 0.97983 9.74E-07
    x 0 7 28 58 0.28027 9.00E-07 30 62 0.1443 2.99E-07 1000 2000 6.9992 7.03E-06 40 82 0.40605 7.77E-07
    x 0 8 74 150 0.69397 9.90E-07 38 78 0.14515 7.85E-07 1000 2000 7.4204 3.07E-06 51 104 0.38454 9.34E-07
    50,000 x 0 1 18 38 0.54115 4.73E-07 30 62 0.47413 7.58E-07 599 1199 13.6056 9.96E-07 42 86 1.2276 9.46E-07
    x 0 2 17 36 0.76665 6.42E-07 36 74 0.86539 4.06E-07 599 1199 14.1491 9.99E-07 36 74 1.2207 9.01E-07
    x 0 3 18 38 0.6784 4.79E-07 40 82 1.1779 5.24E-07 965 1931 22.4849 9.96E-07 34 70 0.76111 9.58E-07
    x 0 4 17 36 0.71341 9.40E-07 26 54 1.1738 7.18E-07 930 1861 19.8461 1.00E-06 25 52 0.54025 9.57E-07
    x 0 5 17 36 0.77557 5.07E-07 31 64 1.0469 3.82E-07 612 1225 13.3692 9.94E-07 80 162 1.2754 9.77E-07
    x 0 6 105 212 2.1942 9.07E-07 43 88 1.4946 4.49E-07 1000 2000 22.6407 1.12E-02 61 124 0.8529 5.43E-07
    x 0 7 25 52 0.89831 9.28E-07 36 74 1.3382 6.77E-07 1000 2000 20.7918 3.23E-06 37 76 0.52293 9.80E-07
    x 0 8 80 162 2.6195 9.55E-07 36 74 1.248 7.34E-07 1000 2000 22.6781 7.26E-06 51 104 0.7567 8.68E-07
    100,000 x 0 1 18 38 0.99539 5.30E-07 29 60 1.3545 7.33E-07 554 1109 28.765 9.98E-07 40 82 2.1423 6.48E-07
    x 0 2 17 36 0.73201 7.00E-07 40 82 2.3368 9.75E-07 550 1101 26.8809 9.95E-07 32 66 1.6289 6.81E-07
    x 0 3 18 38 0.75564 5.03E-07 31 64 1.8121 7.09E-07 902 1805 45.259 9.99E-07 34 70 1.3529 7.52E-07
    x 0 4 17 36 1.4393 9.59E-07 26 54 1.5281 4.49E-07 898 1797 45.4984 9.99E-07 42 86 1.4536 9.22E-07
    x 0 5 17 36 0.96378 5.34E-07 29 60 1.6934 9.80E-07 559 1119 27.9332 9.99E-07 40 82 2.4372 8.74E-07
    x 0 6 106 214 4.3597 9.82E-07 34 70 2.3698 6.79E-07 1000 2000 49.802 1.00E-02 53 108 3.0713 7.13E-07
    x 0 7 25 52 1.0176 6.53E-07 34 70 2.2116 6.72E-07 1000 2000 49.4088 2.79E-06 61 124 3.6486 8.97E-07
    x 0 8 87 176 4.7943 8.91E-07 37 76 1.6038 5.18E-07 1000 2000 48.0059 1.93E-05 52 106 3.1 7.79E-07
    TABLE A5. Numerical results for DFAP1, DFAP2, MHSP, and Algorithm 2.1b for Problem 5 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 11 24 0.032985 5.13E-07 5 12 0.025913 4.32E-08 1 3 0.00475 0.00E+00 1 3 0.008807 0.00E+00
    x 0 2 10 22 0.024207 5.68E-07 4 10 0.036138 2.23E-07 1 3 0.015761 0.00E+00 1 3 0.006042 0.00E+00
    x 0 3 9 20 0.050057 8.46E-07 6 14 0.021645 2.29E-07 6 13 0.023215 0.00E+00 2 5 0.013954 0.00E+00
    x 0 4 12 26 0.038538 2.67E-07 6 14 0.035063 2.74E-07 17 35 0.057828 4.96E-07 4 9 0.023273 0.00E+00
    x 0 5 12 25 0.052322 2.88E-07 11 23 0.078354 5.99E-08 2 5 0.01518 0.00E+00 6 13 0.018798 1.01E-12
    x 0 6 11 24 0.060612 2.37E-07 5 12 0.012572 1.85E-08 1 3 0.006686 0.00E+00 1 3 0.012282 0.00E+00
    x 0 7 12 26 0.029806 2.65E-07 6 14 0.03891 4.79E-07 19 40 0.1164 2.47E-07 4 9 0.018177 0.00E+00
    10,000 x 0 1 11 24 0.042308 7.07E-07 5 12 0.054736 6.05E-08 1 3 0.006823 0.00E+00 1 3 0.01288 0.00E+00
    x 0 2 10 22 0.06149 7.96E-07 4 10 0.043085 3.01E-07 1 3 0.006542 0.00E+00 1 3 0.008923 0.00E+00
    x 0 3 9 20 0.078532 8.46E-07 6 14 0.037246 2.29E-07 6 13 0.044734 0.00E+00 2 5 0.022776 0.00E+00
    x 0 4 12 26 0.11466 3.77E-07 6 14 0.025843 3.88E-07 21 43 0.10073 7.79E-07 4 9 0.023693 0.00E+00
    x 0 5 12 25 0.10853 2.88E-07 11 23 0.042391 5.99E-08 2 5 0.012979 0.00E+00 6 13 0.032398 1.01E-12
    x 0 6 11 24 0.088157 3.34E-07 5 12 0.016573 2.61E-08 1 3 0.01389 0.00E+00 1 3 0.019244 0.00E+00
    x 0 7 12 26 0.060214 3.77E-07 6 14 0.019128 3.08E-07 12 26 0.066176 5.50E-07 4 9 0.039474 0.00E+00
    50,000 x 0 1 12 26 0.31893 3.10E-07 5 12 0.070255 1.34E-07 1 3 0.022681 0.00E+00 1 3 0.031644 0.00E+00
    x 0 2 11 24 0.27318 3.53E-07 4 10 0.066945 6.48E-07 1 3 0.018127 0.00E+00 1 3 0.055765 0.00E+00
    x 0 3 9 20 0.23739 8.46E-07 6 14 0.19919 2.29E-07 6 13 0.076711 0.00E+00 2 5 0.073644 0.00E+00
    x 0 4 12 26 0.3298 8.42E-07 6 14 0.16346 8.67E-07 25 51 0.28353 5.15E-07 4 9 0.15955 0.00E+00
    x 0 5 12 25 0.34985 2.88E-07 11 23 0.33576 5.99E-08 2 5 0.066508 0.00E+00 6 13 0.15499 1.01E-12
    x 0 6 11 24 0.24754 7.48E-07 5 12 0.095493 5.83E-08 1 3 0.024794 0.00E+00 1 3 0.063888 0.00E+00
    x 0 7 12 26 0.23102 8.46E-07 6 14 0.25928 7.54E-07 21 44 0.66008 9.69E-07 4 9 0.079703 0.00E+00
    100,000 x 0 1 12 26 0.78521 4.37E-07 5 12 0.40736 1.90E-07 1 3 0.082085 0.00E+00 1 3 0.045945 0.00E+00
    x 0 2 11 24 0.48157 4.99E-07 4 10 0.18127 9.12E-07 1 3 0.064894 0.00E+00 1 3 0.040479 0.00E+00
    x 0 3 9 20 0.30775 8.46E-07 6 14 0.2456 2.29E-07 6 13 0.32007 0.00E+00 2 5 0.11654 0.00E+00
    x 0 4 13 28 0.40666 2.38E-07 7 16 0.36202 6.11E-09 22 45 1.163 8.55E-07 4 9 0.12853 0.00E+00
    x 0 5 12 25 0.33126 2.88E-07 11 23 0.47871 5.99E-08 2 5 0.087643 0.00E+00 6 13 0.21758 1.01E-12
    x 0 6 12 26 0.30368 2.11E-07 5 12 0.16957 8.24E-08 1 3 0.041519 0.00E+00 1 3 0.037823 0.00E+00
    x 0 7 13 28 0.33086 2.38E-07 7 16 0.28407 7.16E-09 18 37 0.41598 3.51E-07 4 9 0.23262 0.00E+00
    TABLE A6. Numerical results for DFAP1, DFAP2, MHSP, and Algorithm 2.1b for Problem 6 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 4 10 0.018329 6.26E-09 6 14 0.014355 3.36E-08 1 3 0.004235 0.00E+00 1 3 0.008005 0.00E+00
    x 0 2 3 8 0.020542 1.42E-07 5 12 0.011848 2.72E-08 1 3 0.006546 0.00E+00 1 3 0.007326 0.00E+00
    x 0 3 6 14 0.024633 8.36E-08 10 22 0.050635 2.70E-08 2 5 0.010729 0.00E+00 2 5 0.013225 0.00E+00
    x 0 4 6 14 0.031821 2.14E-07 6 14 0.024104 4.55E-08 2 5 0.006148 0.00E+00 2 5 0.011258 0.00E+00
    x 0 5 7 15 0.017524 4.01E-09 11 23 0.025091 2.91E-08 2 5 0.007161 2.22E-16 2 5 0.012327 2.22E-16
    x 0 6 4 10 0.02033 1.65E-09 9 20 0.023269 2.33E-08 2 5 0.005407 0.00E+00 2 5 0.006794 0.00E+00
    x 0 7 6 14 0.042665 2.13E-07 6 14 0.058481 4.53E-08 2 5 0.023084 0.00E+00 2 5 0.019269 0.00E+00
    10,000 x 0 1 4 10 0.047043 3.62E-09 6 14 0.20672 4.75E-08 1 3 0.026036 0.00E+00 1 3 0.012032 0.00E+00
    x 0 2 3 8 0.033992 9.73E-08 5 12 0.070646 3.85E-08 1 3 0.0165 0.00E+00 1 3 0.012194 0.00E+00
    x 0 3 6 14 0.05104 1.81E-07 10 22 0.12792 3.70E-07 2 5 0.048611 0.00E+00 2 5 0.017823 0.00E+00
    x 0 4 6 14 0.04927 2.96E-07 6 14 0.07803 6.43E-08 2 5 0.039948 0.00E+00 2 5 0.013745 0.00E+00
    x 0 5 7 15 0.042205 6.85E-08 10 21 0.15173 2.99E-08 2 5 0.011409 2.22E-16 2 5 0.010604 2.22E-16
    x 0 6 4 10 0.022644 8.76E-10 9 20 0.11432 3.28E-08 2 5 0.021645 0.00E+00 2 5 0.026927 0.00E+00
    x 0 7 6 14 0.03045 2.82E-07 6 14 0.087585 6.43E-08 2 5 0.028601 0.00E+00 2 5 0.02702 0.00E+00
    50,000 x 0 1 12 26 0.22524 6.69E-07 6 14 0.43218 1.06E-07 1 3 0.026552 0.00E+00 1 3 0.051299 0.00E+00
    x 0 2 17 36 0.30629 9.37E-07 5 12 0.2349 8.61E-08 1 3 0.031833 0.00E+00 1 3 0.030024 0.00E+00
    x 0 3 23 48 0.86117 6.28E-07 8 18 0.39886 1.08E-07 2 5 0.059583 0.00E+00 2 5 0.060516 0.00E+00
    x 0 4 23 48 0.82072 8.28E-07 6 14 0.30018 1.44E-07 2 5 0.083815 0.00E+00 2 5 0.088656 0.00E+00
    x 0 5 15 32 0.5765 8.86E-07 9 19 0.29073 2.46E-07 2 5 0.1117 2.22E-16 2 5 0.061876 2.22E-16
    x 0 6 9 20 0.26173 6.70E-07 9 20 0.34041 7.29E-08 2 5 0.078098 0.00E+00 2 5 0.087485 0.00E+00
    x 0 7 23 48 0.48771 8.26E-07 6 14 0.32218 1.44E-07 2 5 0.039331 0.00E+00 2 5 0.11101 0.00E+00
    100,000 x 0 1 12 26 0.47209 9.21E-07 6 14 0.61804 1.50E-07 1 3 0.090865 0.00E+00 1 3 0.075794 0.00E+00
    x 0 2 18 38 0.60246 7.91E-07 5 12 0.37506 1.22E-07 1 3 0.086283 0.00E+00 1 3 0.0593 0.00E+00
    x 0 3 23 48 0.71204 7.53E-07 8 18 0.50419 1.08E-07 2 5 0.21882 0.00E+00 2 5 0.11375 0.00E+00
    x 0 4 24 50 0.71328 7.45E-07 6 14 0.56758 2.03E-07 2 5 0.23029 0.00E+00 2 5 0.10626 0.00E+00
    x 0 5 15 32 1.0405 9.20E-07 9 19 0.43285 2.62E-07 2 5 0.12499 2.22E-16 2 5 0.14361 2.22E-16
    x 0 6 9 20 0.66501 9.05E-07 9 20 0.86707 1.03E-07 2 5 0.12164 0.00E+00 2 5 0.20417 0.00E+00
    x 0 7 24 50 1.4129 7.41E-07 6 14 0.70328 2.03E-07 2 5 0.078027 0.00E+00 2 5 0.20552 0.00E+00
    TABLE A7. Numerical results for DFAP1, DFAP2, MHSP and Algorithm 2.1b for Problem 7 with given initial points and dimensions
    Algorithm 2.1b MHSP DFAP1 DFAP2
    Dimension x0 ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM ITER FVAL TIME NORM
    5000 x 0 1 33 68 0.13924 8.13E-07 5 12 0.014114 9.29E-07 1 3 0.018189 0.00E+00 1 3 0.003967 0.00E+00
    x 0 2 33 68 0.076497 6.64E-07 5 12 0.024362 1.42E-07 1 3 0.004721 0.00E+00 1 3 0.008601 0.00E+00
    x 0 3 26 54 0.052334 6.75E-07 7 16 0.027829 5.03E-07 6 13 0.01289 0.00E+00 5 11 0.026356 0.00E+00
    x 0 4 33 68 0.13849 6.03E-07 18 38 0.094373 5.42E-07 4 9 0.017905 0.00E+00 4 9 0.022803 0.00E+00
    x 0 5 24 50 0.061745 7.76E-07 5 11 0.015022 2.51E-07 1 3 0.010797 2.22E-16 1 3 0.014312 2.22E-16
    x 0 6 32 66 0.055741 9.11E-07 5 12 0.046881 3.04E-07 1 3 0.008507 0.00E+00 1 3 0.011371 0.00E+00
    x 0 7 33 68 0.11548 6.05E-07 14 30 0.043833 8.98E-07 4 9 0.017407 0.00E+00 4 9 0.016641 0.00E+00
    10,000 x 0 1 34 70 0.21118 6.90E-07 6 14 0.029198 1.30E-08 1 3 0.012915 0.00E+00 1 3 0.011272 0.00E+00
    x 0 2 33 68 0.14526 9.39E-07 5 12 0.026215 2.01E-07 1 3 0.007083 0.00E+00 1 3 0.010222 0.00E+00
    x 0 3 26 54 0.12523 6.76E-07 7 16 0.059497 5.16E-07 6 13 0.041298 0.00E+00 5 11 0.044607 0.00E+00
    x 0 4 33 68 0.16049 8.53E-07 10 22 0.11045 5.87E-08 4 9 0.028705 0.00E+00 4 9 0.030026 0.00E+00
    x 0 5 24 50 0.15186 7.76E-07 5 11 0.02664 2.51E-07 1 3 0.013221 2.22E-16 1 3 0.011695 2.22E-16
    x 0 6 33 68 0.20197 7.73E-07 5 12 0.020704 4.30E-07 1 3 0.005691 0.00E+00 1 3 0.009868 0.00E+00
    x 0 7 33 68 0.14239 8.55E-07 13 28 0.033508 8.52E-07 4 9 0.027324 0.00E+00 4 9 0.025958 0.00E+00
    50,000 x 0 1 35 72 0.80962 9.25E-07 6 14 0.15335 2.91E-08 1 3 0.050327 0.00E+00 1 3 0.048888 0.00E+00
    x 0 2 35 72 0.60808 7.56E-07 5 12 0.093206 4.49E-07 1 3 0.029446 0.00E+00 1 3 0.028241 0.00E+00
    x 0 3 26 54 0.49954 6.76E-07 7 16 0.085555 5.26E-07 6 13 0.16531 0.00E+00 5 11 0.12012 0.00E+00
    x 0 4 35 72 0.61249 6.86E-07 15 32 0.44098 3.39E-07 4 9 0.065161 0.00E+00 4 9 0.065034 0.00E+00
    x 0 5 24 50 0.56104 7.76E-07 5 11 0.065801 2.51E-07 1 3 0.027361 2.22E-16 1 3 0.0216 2.22E-16
    x 0 6 35 72 0.8444 6.22E-07 5 12 0.059837 9.62E-07 1 3 0.023185 0.00E+00 1 3 0.016376 0.00E+00
    x 0 7 35 72 0.69601 6.86E-07 25 52 0.42249 9.20E-08 4 9 0.048076 0.00E+00 4 9 0.1062 0.00E+00
    100,000 x 0 1 36 74 1.4092 7.85E-07 6 14 0.21484 4.11E-08 1 3 0.067191 0.00E+00 1 3 0.048954 0.00E+00
    x 0 2 36 74 0.95328 6.42E-07 5 12 0.24899 6.35E-07 1 3 0.075526 0.00E+00 1 3 0.059242 0.00E+00
    x 0 3 26 54 1.1339 6.76E-07 7 16 0.29196 5.28E-07 6 13 0.14947 0.00E+00 5 11 0.21081 0.00E+00
    x 0 4 35 72 1.0982 9.71E-07 18 38 0.53813 9.83E-07 4 9 0.086398 0.00E+00 4 9 0.1823 0.00E+00
    x 0 5 24 50 1.0754 7.76E-07 5 11 0.18151 2.51E-07 1 3 0.061184 2.22E-16 1 3 0.087236 2.22E-16
    x 0 6 35 72 0.94228 8.80E-07 6 14 0.18435 1.35E-08 1 3 0.048094 0.00E+00 1 3 0.088209 0.00E+00
    x 0 7 35 72 1.0376 9.72E-07 11 24 0.49904 1.20E-07 4 9 0.11994 0.00E+00 4 9 0.17879 0.00E+00

    Biographies

    • Auwal Bala Abubakar is a Lecturer II in the Department of Mathematical Sciences, Faculty of Physical Sciences, Bayero University Kano, Nigeria. He holds a masters degree in mathematics (2015) and PhD in Applied Mathematics from King Mongkut's University of Technology Thonburi, Thailand. He is an author of over thirty research papers and his main research interest are methods for solving nonlinear monotone equations with application in signal recovery.

    • Hassan Mohammad received BSc, MSc, and PhD degrees from Bayero University, Kano, Nigeria. During his PhD program, he went to University of Campinas, Campinas, Sao Paulo, Brazil, and Comsat University Islamabad, Pakistan for a twelve-month research visit under the Nigerian Tertiary Education Trust Fund (TETFUND) and the World Academy of Sciences (TWAS) Sandwich Fellowship. He has authored and co-authored a number of research articles in high impact journals. His area of research includes iterative algorithms for solving nonlinear problems such as numerical unconstrained optimization problems, nonlinear least squares problems and system of nonlinear equations.

    • Muhammad Yusuf Waziri is an Associate Professor of Mathematics at Bayero University Kano. He holds a masters degree in mathematics and PhD in Applied Mathematics from University Putra Malaysia. He is an author of over 50 research papers and his main research interest is Methods for solving smooth and nonsmooth system of nonlinear equations.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.