Fractional integro-differential equation (FIDE) with weakly singular kernel is an important topic in mathematics and engineering dealing with mathematical modeling and simulation of numerous systems and processes. A wavelet-based collocation technique has been developed here to obtain approximate numerical solution of a FIDE with weakly singular kernel. The present method avoids complicated integrations and elaborate numerical calculations. The multiscale error approximation associated with this method has also been explained. The efficiency of the proposed method has been demonstrated by including some illustrative examples.

1 Introduction

Application of fractional calculas was introduced by Abel in the solution of integral equation arising in the formulation of tautochrone problem. In recent times different types of integro-differential equations (IDE) and fractional integro-differential equations (FIDE) have been formulated with the purpose of obtaining accurate description of complex phenomena including modeling and simulation of different systems and processes. Among the fractional calculas, FIDE with weakly singular kernel is a relatively new branch in mathematics and has gained considerable popularity and importance due to their vast applications. Many standard mathematical models of integer order derivative including nonlinear models have some limitations to describe the phenomena properly. So, FIDE with different types of singularities have been formulated to describe the physical problems including fracture mechanics, fluid flow, heat conduction problem, dynamical system, and so on.^1-3

The present study concerns with obtaining approximate numerical solution of FIDE with weakly singular kernel of the form

D^{α} y (x) + λ_{1} \int_{0}^{x} \frac{y (t)}{{(x - t)}^{μ}} d t + λ_{2} \int_{0}^{1} V (x, t) d t = f (x), 0 \leq x \leq 1, 0 < α, μ < 1,

()

subject to initial condition

y (0) = 0 .

()

Here $D^{α} y (x)$ represents the fractional derivative of order $α$ of the unknown function y(x) and the fractional derivative is understood in Caputo sense in this paper. The explicit forms of V(x, t) and f(x) are known and they are considered sufficiently smooth to confirm the existence and uniqueness of solution.⁴

Solving of FIDE with weakly singular kernel might be difficult analytically, so many researchers have tried to propose different accurate and efficient numerical methods. In very short time a lot of different numerical methods have been proposed such as spline collocation,⁵ second kind Chebyshev polynomial method,⁶ Legendre wavelets,⁷ an operational Jacobi Tau method,⁸ Hat function,⁹ Shifted Jacobi polynomials,¹⁰ Block pulse,¹¹ Taylor wavelets,¹² and so on. All these methods provide adequate results. Though all these methods have some advantages in some sense but some appeared to be somewhat elaborate. Also in some methods numerical calculations have become unmanageable so as to make the method unattractive. These limitations of mentioned methods together with numerous appearence of FIDE with weakly singular kernel in different fields motivate us to construct a staightforward numerical scheme to solve Equation (1) avoiding numerical complexity.

In this paper, a wavelet-based collocation technique has been proposed to solve FIDE with weakly singular kernel of the form given by (1). The method based on wavelet for solving integral and differential equations has various important features due to multiresolution properties of the space of functions spanned by the wavelets. Wavelet is a special kind of oscillating function and it has been used for decades in digital signal processing and image compression. Here the unknown function in Equation (1) is expanded in tems of wavelet basis of Daubechies family. Under the selection of suitable collocation points, the FIDE is reduced to a system of linear algebraic equations with unknown coefficients involved in the expansion of the unknown function y(x) of FIDE (1). The obtained results are effective in further investigation in the field of FIDE with Cauchy kernel, hypersingular kernel, and other types of special singular kernels.

2 Basic preliminaries and notations

2.1 The fractional derivative and integrals

There exists a vast literature on various types of definitions on fractional derivatives (FD) and fractional integrals (FI). The conventional definitions of fractional derivatives include Caputo FD, Riemann-Liouville FD, Caputo -Frabizio FD, Atangana-Baleana FD, Riesz FD, and so on. Also the conventional definitions of fractional integrals include Riemann-Liouville FI, Hadamard FI, Atangana-Baleana FI, and so on. The widely used definition of FD is the Caputo definition and FI is the Riemann–Liouville definition.

Definition 1.Caputo's fractional derivative of order $α$ is defined as¹²

D^{α} f (x) = \frac{1}{Γ (n - α)} \int_{0}^{x} \frac{f^{(n)} (t)}{{(x - t)}^{α + 1 - n}} d t, n - 1 < α \leq n, n \in ℕ,

()

where

α > 0

is the order of the derivative and n is the smallest integer greater than

α

Definition 2.The Riemann–Lioville fractional integral operator of order $α$ is defined as¹²

I^{α} f (x) = \{\begin{cases} \frac{1}{Γ (α)} \int_{0}^{x} \frac{f (t)}{{(x - t)}^{- α}} d t = \frac{1}{Γ (α)} x^{α - 1} * f (x) & α > 0 \\ f (x) & α = 0, \end{cases}

()

where

x^{α - 1} * f (x)

is the convolution product of

x^{α - 1}

and f(x).

The relation between the Riemann–Lioville operator and Caputo operator is given below

I^{α} D^{α} f (x) = f (x) - \sum_{i = 0}^{n - 1} f^{i} (0) \frac{x^{i}}{i!} .

()

2.2 Collocation method

Collocation method is introduced in mathematics to find approximate numerical solution of differential equations (ODE and PDE) and integral equations including IDE and FIDE. Detail description of collocation method is available in any standard book (see Reference 13). The convergency of collocation method depends on suitable choice of collocation points and basis of some finite-dimensional space of functions. We can consider any type of integral or differential equations to understand the convergence of this method. Here we consider the following integral equation

u (x) + λ \int_{Ω} L (x, t) u (t) d t = g (x), x \in Ω \subseteq ℝ .

()

We consider here u_n(x) to be the approximate solution of the exact solution u(x) of Equation (6). u_n(x) can be expanded in the linear span of some basis

\{θ_{1} (x), θ_{2} (x), \dots, θ_{n} (x)\}

of finite-dimensional space of functions, that is,

u_{n} (x) = \sum_{k = 1}^{n} ζ_{k} θ_{k} (x) .

()

The basic idea is to choose the distinct points x_i (i = 1, 2, … , n) from

Ω

so that Equation (6) is reduced to the form

u (x_{i}) + λ \int_{Ω} L (x_{i}, t) u (t) d t = g (x_{i}), (i = 1, 2, 3, \dots, n) .

()

The system of Equations (8) determines the n unknown coefficients

\{ζ_{1}, ζ_{2}, \dots, ζ_{n}\}

as the solution of the linear system

\sum_{k = 1}^{n} ζ_{k} [θ_{k} (x_{i}) + λ \int_{Ω} L (x_{i}, t) θ_{k} (t) d t] = g (x_{i}), (i = 1, 2, 3, \dots, n) .

()

We consider here that the linear system contains integrals that have to be evaluated numerically. A number of questions arises such as whether the system has a solution, and if so, whether it is unique. If the system has unique solution then the method should be convergent as the unknown function is expressed in terms of basis elements. If the system (9) has unique solution then the system

\sum_{k = 1}^{n} ζ_{k} θ_{k} (x_{i}) = u_{n} (x_{i}) (i = 1, 2, \dots, n),

()

also has unique solution. The system (10) has unique solution if det

[θ_{k} (x_{i})] \neq 0 .

This is the necessary condition whether the collocation method can be used or not.

2.3 Multiscale (wavelet) basis of Daubechies family

Trigonometric functions, exponential functions or orthogonal polynomials associated with some self-adjoint operators are used as basic building blocks to approximate a function or represent an operator in approximation theory. If the building block contains n elements, then the operators or functions are constituted by n × n matrix and n × 1 vectors respectively. In the action of functions or operators, O(n²) or O(n⁴) operations are needed. So if n increases, then a large number of operations is needed. A comprehensive mathematical theory known as multiresolution analysis (MRA) has received considerable attention to overcome the limitation mentioned above. Daubechies invented a compactly supported orthogonal wavelet basis that can be generated from a single function known as scale function with the aim to serve the MRA of $L^{2} (ℝ)$ .

The definition of a MRA of

L^{2} (ℝ)

(assumed to have Hilbert space structure) with the scale function

ϕ (x)

of Daubechies family and properties of scale function and wavelet functions are available in any standard books and research articles (see^{13, 14}). The scale function and wavelet function having compact support

[a^{*}, b^{*}]

satisfy the following relations known as two-scale relations

ϕ (x) = \sqrt{2} \sum_{l = a^{*}}^{b^{*}} h_{l} ϕ (2 x - l),

()

and

ψ (x) = \sqrt{2} \sum_{l = a^{*}}^{b^{*}} g_{l} ϕ (2 x - l) .

()

The two scale relations for nth order derivative of the scale function

ϕ (x)

and wavelet function

ψ (x)

are obtained from (11) and (12) followed by differentiating n times

ϕ^{(n)} (x) = 2^{n + \frac{1}{2}} \sum_{l = a^{*}}^{b^{*}} h_{l} ϕ^{n} (2 x - l),

()

and

ψ^{(n)} (x) = 2^{n + \frac{1}{2}} \sum_{l = a^{*}}^{b^{*}} g_{l} ϕ^{n} (2 x - l),

()

where h_l and g_l

(l = a^{*}, a^{*} + 1, \dots, b^{*})

are known as low-pass and high-pass filter coefficients, respectively. For the wavelet of Daubechies family with compact support [0, 2K − 1] there exists 2K low-pass filter coefficients h_l (l = 0, 1, 2, … , 2K − 1) and 2K high-pass filter coefficients g_l (l = 0, 1, 2, … , 2K − 1) and they are related by the relation g_l = (− 1)^lh_{2K − 1 − l}. The elements in the collection

{\{ϕ_{j k} (x) = 2^{\frac{j}{2}} ϕ (2^{j} x - k)\}}_{k \in ℤ}

take the important role in approximation theory to expand the unknown functions in the approximation space V_j. Though k belongs to

ℤ

but for the finite interval [a, b], few elements in the collection do not overlap completely in [0, 2K − 1] for some values of k. Hence some properties (viz. translation, orthogonalization, etc.) of scale function do not hold good. To control this problem, we split the translates of

ϕ (x)

for a particular resolution j into three classes as

Λ_{j}^{L}, Λ_{j}^{I}, and Λ_{j}^{R}

.¹³

3 Method of approximation

We have to take the consideration y(0) = 0 and det

[ϕ_{j k} (k^{'})] \neq 0

(

k^{'}

are collocation points) to be fulfilled in the approximation of the unknown function y(x) of FIDE (1). We approximate y(x) in the approximation space V_j as

\begin{align} y (x) \approx y_{j}^{M S} (x) & = \sum_{k = 0}^{2^{j} - 1} c_{j k}^{s} ϕ_{j k}^{s} (x), s = I or R \\ = C_{j}^{T} {\vec{Φ}}_{j} (x) . \end{align}

()

The approximation of the nth derivative of the unknown function y(x) is given by

\begin{align} y^{(n)} (x) & \approx 2^{n j} \sum_{k = 0}^{2^{j} - 1} c_{j k}^{s} ϕ_{j k}^{n s} (x), s = I or R \\ = 2^{n j} C_{j}^{T} {\vec{Φ}}_{j (n)} (x), \end{align}

()

where

ϕ_{j k}^{n s} (x) = 2^{\frac{j}{2}} ϕ^{n s} (2^{j} x - k) .

()

Here

C_{j}, {\vec{Φ}}_{j} (x), and {\vec{Φ}}_{j (n)} (x)

all are 2^j × 1 vectors, given by

C_{j} = {[c_{j 0}^{I}, c_{j 1}^{I}, \dots, c_{j 2^{j} - 2 K + 1}^{I}, c_{j 2^{j} - 2 K + 2}^{R}, \dots, c_{j 2^{j} - 1}^{R}]}^{T},

()

{\vec{Φ}}_{j} (x) = {[ϕ_{j 0}^{I} (x), ϕ_{j 1}^{I} (x), \dots, ϕ_{j 2^{j} - 2 K + 1}^{I} (x), ϕ_{j 2^{j} - 2 K + 2}^{R} (x), \dots, ϕ_{j 2^{j} - 1}^{R} (x)]}^{T},

()

and

{\vec{Φ}}_{j (n)} (x) = {[ϕ_{j 0}^{n I} (x), ϕ_{j 1}^{n I} (x), \dots, ϕ_{j 2^{j} - 2 K + 1}^{n I} (x), ϕ_{j 2^{j} - 2 K + 2}^{n R} (x), \dots, ϕ_{j 2^{j} - 1}^{n R} (x)]}^{T} .

()

Using the Caputo definition of fractional derivative and the approximate form of y(x) and y⁽ⁿ⁾(x) found in (15) and (16), Equation (1) is reduced to the form

C_{j}^{T} [\frac{2^{n j}}{Γ (n - α)} \int_{0}^{x} \frac{ϕ_{j k}^{n s} (t) d t}{{(x - t)}^{α}} + λ_{1} \int_{0}^{x} \frac{ϕ_{j k}^{s} (t) d t}{{(x - t)}^{μ}} + λ_{2} \int_{0}^{1} V (x, t) ϕ_{j k}^{s} d t] = f (x) .

()

We choose total 2^j numbers of collocation points as

x_{j k^{'}} = \frac{k^{'}}{2^{j}} (k^{'} = 1, 2, \dots, 2^{j})

from the interval [0, 1]. Under this choice of collocation points, the equation (21) gives rise to the system of linear equations

C_{j}^{T} [\frac{2^{n j}}{Γ (n - α)} A_{j}^{(k^{'})} + λ_{1} B_{j}^{(k^{'})} + λ_{2} C_{j}^{(k^{'})}] = f (\frac{k^{'}}{2^{j}}) .

()

Here

A_{j}^{(k^{'})}, B_{j}^{(k^{'})}, and C_{j}^{(k^{'})}

all are 2^j × 2^j matrix and their respective matrix elements are given by

J_{α j}^{(n)} (k^{'}, k) = \int_{0}^{\frac{k^{'}}{2^{j}}} \frac{ϕ_{j k}^{n s} (t) d t}{{(\frac{k^{'}}{2^{j}} - t)}^{α}},

()

I_{μ j} (k^{'}, k) = \int_{0}^{\frac{k^{'}}{2^{j}}} \frac{ϕ_{j k}^{s} (t) d t}{{(\frac{k^{'}}{2^{j}} - t)}^{μ}},

()

Q_{j} (k^{'}, k) = \int_{0}^{1} V (\frac{k^{'}}{2^{j}}, t) ϕ_{j k}^{s} (t) d t .

()

The superscript s in $ϕ_{j k}^{s} (t)$ and $ϕ_{j k}^{n s} (t)$ will be I or R according as $k \in Λ_{j}^{I} or Λ_{j}^{R}$ . Equation (22) represents a system of 2^j number of algebraic equations with 2^j number of unknown coefficients $c_{j k}^{s}$ . After determining $c_{j k}^{s}$ , the value of the unknown function y(x) can be determined at any dyadic point in [0, 1]. In order to calculate y(x) at any arbitrary point x other than dyadic point, the dyadic approximation of x has to be used.¹⁵

4 Evaluation of matrix elements

To determine the unknown coefficients $c_{j k}^{s}$ involved in the expansion of the unknown function of FIDE in terms of basis of Daubechies family, we have to calculate numerical values of the elements of each of the matrices $A_{j}^{(k^{'})}, B_{j}^{(k^{'})}, and C_{j}^{(k^{'})}$ . Hence the prime task for wavelet-based collocation method for FIDE with weakly singular kernel is the numerical evaluation of the integrals $J_{α j}^{(n)} (k^{'}, k), I_{μ j} (k^{'}, k)$ and $Q_{j} (k^{'}, k)$ .

4.1 Evaluation of $J_{α j}^{(n)} (k^{'}, k)$

Using the expression

ϕ_{j k}^{n} (t) = 2^{\frac{j}{2}} ϕ^{n} (2^{j} t - k)

in the integral (23), we get

J_{α j}^{(n)} (k^{'}, k) = 2^{(α - \frac{1}{2}) j} 𝒯_{α}^{(n)} (k^{'} - k),

()

where

𝒯_{α}^{(n)} (k) = \int_{0}^{k} \frac{ϕ^{(n)} (t) d t}{{(k - t)}^{α}} .

()

The support of $ϕ (t)$ and $ϕ^{(n)} (t)$ is [0, 2K − 1] for Dau-K family of scale function. If k ≤ 0, then range of integration in (27) and the support [0, 2K − 1] have no nonempty intersection. Hence, if k ≤ 0, $J_{α j}^{(n)} (k^{'}, k)$ vanishes.

Also

𝒯_{α}^{(n)} (k)

has no singularity within support [0, 2K − 1] for k ≥ 2K. In this case integrating (27) by parts successively n times, we get

𝒯_{α}^{(n)} (k) = {(- 1)}^{n} α^{\overline{n}} \int_{ℝ} \frac{ϕ (t) d t}{{(k - t)}^{α + n}},

()

where

α^{\overline{n}} = α (α + 1) (α + 2) . . . (α + n - 1)

is the rising factorial or Pochhamaner polynomial. Using M-(M ≥ 1) point Gauss type quadrature rule involving Daubechies scale function and a continuous function,¹⁶

𝒯_{α}^{(n)} (k)

can be evaluated as

𝒯_{α}^{(n)} (k) = {(- 1)}^{n} α^{\overline{n}} \sum_{i = 1}^{M} \frac{w_{i}^{I}}{{(k - t_{i}^{I})}^{α + n}},

()

where

w_{i}^{I}

and

t_{i}^{I} (i = 1, 2, \dots, M)

are the weights and nodes for the full support[0, 2K − 1].

If 0 < k ≤ 2K − 1, then

𝒯_{α}^{(n)} (k)

has integrable singularity at the upper limit k, so quadrature rule can not be applied to find

𝒯_{α}^{(n)} (k)

for 0 < k ≤ 2K − 1. The quadrature rule does not provide results with desired order of accuracy for this case. In this case using two scale relation (13) for the nth order derivative of the scale function in Equation (27), we get

𝒯_{α}^{(n)} (k) = 2^{n + α - \frac{1}{2}} \sum_{l = 0}^{2 K - 1} h_{l} 𝒯_{α}^{(n)} (2 k - l) .

()

Using the symbols

ℋ_{K} = (\begin{matrix} h_{1} & h_{0} & 0 & 0 \dots & 0 & 0 \\ h_{3} & h_{2} & h_{1} & h_{0} \dots & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ \dots & ⋮ & ⋮ \\ 0 & 0 & 0 & 0 \dots & h_{2 K - 2} & h_{2 K - 3} \\ 0 & 0 & 0 & 0 \dots & 0 & h_{2 K - 1} \end{matrix}),

()

and

b_{α K}^{(n)} = 2^{n + α - \frac{1}{2}} (\begin{matrix} 0 \\ 0 \\ ⋮ \\ \sum_{l = 0}^{2 K - 4} h_{l} 𝒯_{α}^{(n)} (4 K - 4 - l) \\ \sum_{l = 0}^{2 K - 2} h_{l} 𝒯_{α}^{(n)} (4 K - 2 - l) \end{matrix}) .

()

The recurrence relation (30) can be written in the form

(I - 2^{n + α - \frac{1}{2}} ℋ_{K}) {𝒯_{α}}^{(n)} = b_{α K}^{(n)} .

()

So, the singular integrals

𝒯_{α}^{(n)} (k) (k = 0, 1, \dots, 2 K - 1)

can be found as the elements of the matrix

𝒯_{α}^{(n)}

𝒯_{α}^{(n)} = {(I - 2^{n + α - \frac{1}{2}} ℋ_{K})}^{- 1} b_{α K}^{(n)} .

()

Thus, evaluation of

𝒯_{α}^{(n)} (k)

is summarized as

𝒯_{α}^{(n)} (k) = \{\begin{cases} 0 & k \leq 0, \\ solution obtained by (34) & 1 \leq k \leq 2 K - 1, \\ {(- 1)}^{n} α^{\overline{n}} \sum_{i = 1}^{M} \frac{w_{i}^{I}}{{(k - t_{i}^{I})}^{α + n}} & k \geq 2 K . \end{cases}

()

In the evaluation of $𝒯_{α}^{(n)} (k)$ , the values of n depend on $α$ as $n - 1 < α \leq n .$ Table 1 displays the values of $𝒯_{α}^{(n)} (k)$ for (k = 0, 1, 2, … , 2K − 1) taking Daubechies family of wavelets with K = 3 for $α = 0.25, 0.5 and 0.75$ . In this calculation n = 1 is taken as $α \in (0, 1)$ . $𝒯_{α}^{(n)} (k)$ can be evaluated for any other values of $α$ using the formula (35).

TABLE 1. Values of

𝒯_{α}^{(n)} (k)

k	$α = 0.25$	$α = 0.50$	$α = 0.75$
1	1.77224	2.78268	5.94309
2	−1.13093	−2.56704	−6.90373
3	0.12730	0.36169	1.32940
4	−0.04753	−0.05757	0.00573
5	−0.04176	−0.05839	−0.06126

The order

α

of the fractional derivative of the unknown function y(x) involved in the equation (1) is considered to satisfy the condition

0 < α < 1

. At this stage one question arises -what will happen for

α = 1 ?

The matrix

(I - 2^{n + α - \frac{1}{2}} ℋ_{K})

is a bad conditional matrix for

α = 1

. So, a large amount of computational error may occur to determine

𝒯_{α}^{(n)} (k) (k = 0, 1, 2, \dots, 2 K - 1)

. Moreover this is also noticeable that

Γ (n - α)

is undefined for

α = 1

. The wavelet-based collocation method is to be suitably modified for integer order derivative

(e.g., α = 1) .

If we consider the integer values of

α

, the derivative of the unknown function y(x) of order

α

takes the form

y^{(α)} (x) \approx 2^{α j} C_{j}^{T} {\vec{Φ}}_{j (α)} (x) .

The system of Equations (22) takes the form

C_{j}^{T} [2^{α j} {\tilde{A}}_{j}^{(k^{'})} + λ_{1} B_{j}^{(k^{'})} + λ_{2} C_{j}^{(k^{'})}] = f (\frac{k^{'}}{2^{j}}) .

()

Here

{\tilde{A}}_{j}^{(k^{'})}

is also a 2^j × 2^j matrix and its matrix elements are given by

{\tilde{J}}_{α j} (k^{'}, k) = ϕ_{j k}^{α s} (\frac{k^{'}}{2^{j}}) = ϕ^{α} (p) .

()

Here

p = k^{'} - k, (k^{'} = 1, 2, \dots, 2^{j}, k = 0, 1, \dots, 2^{j} - 1)

is an integer. As the support of both

ϕ (x)

and

ϕ^{α} (x)

is [0, 2K − 1] for Dau-K family of wavelets, so

ϕ^{α} (p)

vanishes for p ∈ (−∞, 0) ∪ (2K − 1, ∞). The continuity of

ϕ^{α} (x)

assures that

ϕ^{α} (p) = 0

for p = 0, 2K − 1. The nonzero values of

ϕ^{α} (p), (p = 1, 2, \dots, 2 K - 2)

can be obtained with the help of recurrence relation

ϕ^{α} (p) = 2^{n + \frac{1}{2}} \sum_{l = 0}^{2 K - 1} h_{l} ϕ^{α} (2 p - l),

()

in conjunction with the normalization condition

α! = \sum_{l = 0}^{2 K - 1} l^{α} ϕ^{α} (p - l) .

()

This recurrence relation follows from Equation (13) and normalization condition is constructed with the help of determination of unknown coefficients involved in the expansion of $x^{α}$ in terms of Daubechies scale functions at zero scale level over $ℝ$ .

4.2 Evalution of $I_{μ j} (k^{'}, k)$

The calculation procedure for the matrix elements

I_{μ j} (k^{'}, k)

is quite similar with the calculation procedure of the matrix elements

J_{α j}^{(n)} (k^{'}, k)

. Using the expression

ϕ_{j k} (t) = 2^{\frac{j}{2}} ϕ (2^{j} t - k)

in the integral (24), we get

I_{μ j} (k^{'}, k) = 2^{(μ - \frac{1}{2}) j} ℒ_{μ} (k^{'} - k),

()

where

ℒ_{μ} (k) = \int_{0}^{k} \frac{ϕ (t) d t}{{(k - t)}^{μ}} .

()

ℒ_{μ} (k)

vanishes for k ≤ 0, as the range of the integration in (49) is completely outside of the support [0, 2K − 1] of the scale function. Again if

k \geq 2 K, ℒ_{μ} (k)

has no singularity within the support [0, 2K − 1]. Using Gauss Daubechies quadrature rule involving Daubechies scale function,¹⁶

ℒ_{μ} (k)

is evaluated as

ℒ_{μ} (k) = \sum_{i = 1}^{M} \frac{w_{i}^{I}}{{(k - t_{i}^{I})}^{μ}}, (k \geq 2 K) .

()

Here $w_{i}^{I}$ , $t_{i}^{I}$ are weights are nodes of Gauss Daubechies quadrature rule involving Daubechies scale function.¹⁶

0 < k \leq 2 K - 1, ℒ_{μ} (k)

has integrable singularity at the upper limit so that evaluation of such integrals by using the quadrature rule may not provide their approximate value with desired order of accuracy within less computational time. The recurrence relation for

ℒ_{μ} (k)

can be obtained as

ℒ_{μ} (k) = 2^{μ - \frac{1}{2}} \sum_{l = 0}^{2 K - 1} h_{l} ℒ_{μ} (2 k - l) .

()

Using the symbol used in (31) and using the symbol

b_{μ K} = 2^{(μ - \frac{1}{2})} (\begin{matrix} 0 \\ 0 \\ ⋮ \\ \sum_{l = 0}^{2 K - 4} h_{l} ℒ_{μ} (4 K - 4 - l) \\ \sum_{l = 0}^{2 K - 2} h_{l} ℒ_{μ} (4 K - 2 - l) \end{matrix})

()

the relation (43) can be put in the form

(I - 2^{μ - \frac{1}{2}} ℋ_{K}) ℒ_{μ} = b_{μ K} .

()

So, the singular integrals in

ℒ_{μ}

are found as

ℒ_{μ} = {(I - 2^{μ - \frac{1}{2}} ℋ_{K})}^{- 1} b_{μ K} .

()

Thus, evaluation of

ℒ_{μ} (k)

is summarized as

ℒ (k) = \{\begin{cases} 0 & k \leq 0, \\ solution obtained by (46) & 1 \leq k \leq 2 K - 1, \\ \sum_{i = 0}^{M} \frac{w_{i}}{{(k - t_{i})}^{μ}} & k \geq 2 K . \end{cases}

()

In Table 2 the values of $ℒ (k)$ for k = 1, 2, … , 5 are given taking Dau-3 scale function for $μ = 0.25, 0.5, and 0.75$ . For other values of $μ (0 < μ < 1)$ these can be easily calculated.

TABLE 2. Values of

ℒ (k)

k	$μ = 0.25$	$μ = 0.50$	$μ = 0.75$
1	0.925995	1.643812	4.018044
2	1.064183	0.954199	0.410716
3	0.808341	0.682604	0.691069
4	0.748236	0.560703	0.424904
5	0.699178	0.488824	0.341744

4.3 Evaluation of $Q_{j} (k^{'}, k)$

Using the expression for

ϕ_{j k} (x) = 2^{\frac{j}{2}} ϕ (2^{j} x - k)

and transforming the variable, the integral (25) takes the form

Q_{j} (k^{'}, k) = \frac{1}{2^{\frac{j}{2}}} \int_{0}^{2^{j} - k} V (\frac{k^{'}}{2^{j}}, \frac{t + k}{2^{j}}) ϕ (t) d t, k^{'} = 0, 1, 2, \dots, 2^{j} .

()

Using M- point quadrature rule (M ≥ 1) involving a continuous function and a scale function once again , we get

Q_{j} (k^{'}, k) = \{\begin{cases} \frac{1}{2^{\frac{j}{2}}} \sum_{i = 1}^{M} w_{i}^{I} V (\frac{k^{'}}{2^{j}}, \frac{t_{i}^{I} + k}{2^{j}}) & if k \in Λ_{j}^{I}, \\ \frac{1}{2^{\frac{j}{2}}} \sum_{i = 1}^{M} w_{i}^{R} (k) V (\frac{K^{'}}{2^{j}}, \frac{t_{i}^{R} (k) + k}{2^{j}}) & if k \in Λ_{j}^{R} . \end{cases}

()

If $k \in Λ_{j}^{I}$ , then the range of integration [0, 2^j − k] is equivalent to [0, 2K − 1], support of the scale function $ϕ (t)$ . Again if $k \in Λ_{j}^{R}$ , then the range of integration is converted to $[0, s] (s = 2^{j} - k \in \{2 K - 2, 2 K - 1, \dots, 1\})$ . $w_{i}^{I}, t_{i}^{I} (i = 1, 2, \dots, M)$ are the weights and nodes for the full support [0.2K − 1] as range of integration. $w_{i}^{R} (k), t_{i}^{R} (k) (i = 1, 2, \dots, M)$ are the weights and nodes for the the partial support $[0, s], (s = 2^{j} - k, k \in Λ_{j}^{R})$ as the range of integration. The values of $w_{i}^{R} (k), w_{i}^{I} and t_{i}^{R} (k), t_{i}^{I}$ are tabulated in the tables 6.7 and 6.8 in the article.¹⁶

5 Multiscale approximation and Error estimation

Computed results of

c_{j k}^{s} (k = 0, 1, 2, \dots, 2^{j} - 1)

are used to find multiscale approximation of the unknown function y(x) ∈ L²([0, 1]). The projection of y(x) into the approximation space

V_{j} (linear span of ϕ_{j k} (x))

is used in Equation (15). It is known that Clos

_{L^{2}} (V_{j} \oplus_{j^{*} = j}^{\infty} W_{j^{*}}) (j^{*} \geq j)

gives the complete information of a function in

L^{2} (ℝ) .

The multiscale approximation of y(x) in L²([0, 1]) is given by the projection of y(x) into the approximation space V_j and the detail space

W_{j} (linear span of ψ_{j k} (x))

y (x) = \sum_{k = 0}^{2^{j} - 1} c_{j k}^{s} ϕ_{j k}^{s} (x) + \sum_{j^{*} = j}^{\infty} \sum_{k = 0}^{2^{j^{*}} - 1} d_{j^{*} k}^{s} ψ_{j^{*} k}^{s} (x), s = I, R .

()

Φ_{j} = \{ϕ_{j 0}^{I} (x), ϕ_{j 1}^{I} (x), \dots, ϕ_{j 2^{j} - 1}^{R} (x)\}

and

Ψ_{j} = \{ψ_{j 0}^{I} (x), ψ_{j 1}^{I} (x), . . ., ψ_{j 2^{j} - 1}^{R} (x)\}

are taken here as the basis of the approximation space V_j and the detail space W_j for any function in L²([0, 1]) to serve the calculation without violating the properties of scale and wavelet functions. The coefficients

c_{j k}^{s}

and

d_{j k}^{s}

can be determined using the orthonormal property of scale function and wavelet function for any function in

L^{2} (ℝ)

. In this case, the orthonormality property has been lost for few elements in basis set

Φ_{j}

and

Ψ_{j}

. The technique to determine

c_{j k}^{s} and d_{j k}^{s}

are described below. At this stage the following notations are used for convenience

and

N_block and T_block are the partitioned matrix of

N \equiv {(N_{j : k k^{'}})}_{(2^{j} + 2 K - 2) \times (2^{j} + 2 K - 2)}

and

T \equiv {(T_{j : k k^{'}})}_{(2^{j} + 2 K - 2) \times (2^{j} + 2 K - 2)}

, respectively. The detail trick for calculating the matrix elements

N_{j : k k^{'}} = \int_{0}^{1} ϕ_{j k}^{s} (x) ϕ_{j k^{'}}^{s^{'}} (x) d x (k, k^{'} \in Λ_{j}^{L or I or R} and s, s^{'} = L or I or R)

are described in Reference 14. The matrix elements

T_{j : k k^{'}} = \int_{0}^{1} ψ_{j k}^{s} (x) ψ_{j k^{'}}^{s^{'}} (x) d x (k, k^{'} \in Λ_{j}^{L or I or R} and s, s^{'} = L or I or R)

is identical with

δ_{k k^{'}}

for

k, k^{'} \in Λ_{j}^{I}

. This follows from orthonormal property of wavelet function. For other values of

k and k^{'}

the matrix elements

T_{j : k k^{'}}

can be determined from relation

T_{_{j : k k^{'}}} = \sum_{l_{1} = 0}^{2 K - 1} \sum_{l_{2} = 0}^{2 K - 1} g_{l_{1}} g_{l_{2}} N_{_{j + 1 : 2 k + l_{1} 2 k^{'} + l_{2}}},

()

which is obtained by using the expression

ψ_{j k} (x) = 2^{^{\frac{j}{2}}} ψ (2^{^{j}} x - k)

and two scale relation (12). The coefficients

c_{j k}^{s}

and

d_{j k}^{s}

are determined as the matrix elements of C and D as

C^{T} = M N_{block}^{−1},

()

D^{T} = U T_{block}^{−1} .

()

N_block and T_block both are 2^j × 2^j matrices. M and U are 1 × 2^j matrices and their respective matrix elements

m_{j : k} (k \in Λ_{j}^{I or R})

and

u_{j : k} (k \in Λ_{j}^{I or R})

are given by

m_{j : k} = \int_{- 1}^{1} y (x) ϕ_{j k}^{s} d x, s = I, R,

()

u_{j : k} = \int_{- 1}^{1} y (x) ψ_{j k}^{s} d x, s = I, R .

()

Using the two-scale relations (11) and (12), the m_j : k and u_j : k can be written as

m_{j : k} = \{\begin{cases} \sum_{l = 0}^{2 K - 1} h_{l} c_{j + 1, 2 k + l}^{S} & if k \in Λ_{j}^{I} \\ \sum_{l = 0}^{2 K - 1} h_{l} c_{j + 1, 2 k + l}^{S} N_{j + 1 : 2 k + l, k_{1}} & if k \in Λ_{j}^{R} . \end{cases}

()

and

u_{j : k} = \{\begin{cases} \sum_{l = 0}^{2 K - 1} g_{l} c_{j + 1, 2 k + l}^{S} & if k \in Λ_{j}^{I} \\ \sum_{l = 0}^{2 K - 1} g_{l} c_{j + 1, 2 k + l}^{S} N_{j + 1 : 2 k + l, k_{1}} & if k \in Λ_{j}^{R} . \end{cases}

()

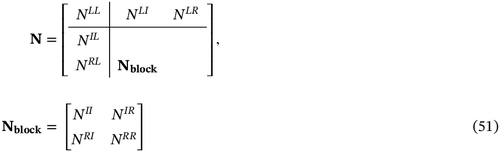
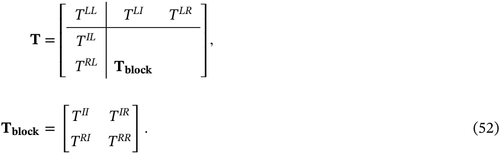
In Equations (58) and (59), if k takes the values b2^j − r (r = 2K − 2, 2K − 3, … , 1) from $Λ_{j}^{R}$ then k₁ takes the values b2^j + 1 − r (r = 2K − 2, 2K − 3, … , 1) from $Λ_{j + 1}^{R}$ . The main aim here is to calculate the values of $d_{j k}^{s}$ , as $c_{j k}^{s}$ are determined in the preceding section. The coefficients $d_{j k}^{s}$ can be determined by the matrix equation (55) after expressing the matrix U using the relation (59). One needs the coefficients $c_{j + 1 k}^{s}$ at level j + 1 to evaluate $d_{j k}^{s}$ at level j.

Now using the expression for

y_{j}^{MS} (x)

found in (15), the equation (50) is reduced to the form

y (x) = y_{j}^{MS} (x) + \sum_{j^{*} = j}^{\infty} δ y_{j^{*}} (x),

()

where

δ y_{j^{*}} (x) = \sum_{k = 0}^{2^{j^{*} - 2 K + 1}} d_{j^{*} k}^{I} ψ_{j^{*} k}^{I} (x) + \sum_{k = 2^{j^{*} - 2 K + 2}}^{2^{j^{*} - 1}} d_{j^{*} k}^{R} ψ_{j^{*} k}^{R} (x) .

()

Therefore, the error e(x) in multiscale approximation is given by

e (x) = y (x) - y_{j}^{MS} (x) = \sum_{j^{*} = j}^{\infty} δ y_{j^{*}} (x) .

()

Using the concept of L²-norm, inner product for L² and Minkowski inequality the upper bound of the square of L²-norm of multiscale error

‖ e (x) ‖_{L^{2} [0, 1]}^{2}

at level j can be guessed from the inequality

‖ e (x) ‖_{L^{2} [0, 1]}^{2} \leq ‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2} \frac{1}{1 - τ},

()

where

τ = \max_{η} \frac{‖ δ y_{j + η} (x) ‖_{L^{2} [0, 1]}^{2}}{‖ δ y_{j + η - 1} (x) ‖_{L^{2} [0, 1]}^{2}}

for

η = 1, 2, 3, . . .

and it is found that

τ

satisfies the condition

0 < τ < 1

. The value of

‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2}

is obtained by using orthonormality property of

ψ_{j k} (x)

for full support and the equation (53) for the partial support of

ψ_{j k} (x)

\begin{align} ‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2} & = < \sum_{k = 0}^{2^{j} - 1} d_{j k}^{s} ψ_{j k}^{s} (x), \sum_{k = 0}^{2^{j} - 1} d_{j k}^{s} ψ_{j k}^{s} (x) > \\ = \sum_{k^{'} = 0}^{2^{j} - 2 K + 1} \sum_{k = 0}^{2^{j} - 2 K + 1} d_{j k}^{I} d_{j k^{'}}^{I} δ_{k^{'} k} + \sum_{k = 2^{j} - 2 K + 2}^{2^{j} - 1} \sum_{k^{'} = 2^{j} - 2 K + 2}^{2^{j} - 1} d_{j k}^{R} d_{j k^{'}}^{R} T_{j : k^{'} k}^{R} . \end{align}

()

In the above calculation, the terms $\int_{0}^{1} ψ_{j k}^{I} (x) ψ_{j k^{'}}^{R} (x) d x$ and $\int_{0}^{1} ψ_{j k}^{R} (x) ψ_{j k^{'}}^{I} (x) d x$ are neglected as they take values zero or nearly zero.

6 Illustrative examples

Here, three examples are given to test the efficiency of wavelet-based collocation technique developed here in the numerical solution of FIDE.

Example 1

Consider the following FIDE with weakly singular kernel as¹²

D^{0.25} y (x) - \frac{1}{2} \int_{0}^{x} \frac{y (t)}{{(x - t)}^{\frac{1}{2}}} d t - \frac{1}{3} \int_{0}^{1} (x - t) y (t) d t = f (x),

()

with initial condition

y (0) = 0,

where

f (x) = \frac{Γ (3)}{Γ (2.75)} x^{1.75} + \frac{Γ (4)}{Γ (3.75)} x^{2.75} - \frac{\sqrt{π} Γ (3)}{2 Γ (4.5)} x^{3.5} - \frac{7}{36} x + \frac{3}{20} .

The exact solution of this problem is y(x) = x² + x³.

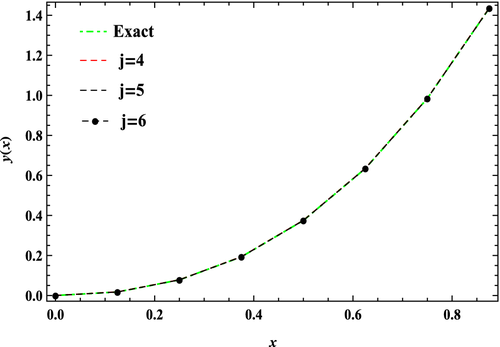
In Table 3, the approximate solution obtained by present method at the resolution level j = 4, 5, 6 together with the exact solution y(x) of example 1 are shown at the points $x = \frac{ζ}{8} (ζ = 0, 1, 2, . . . ., 7) .$ To find approximate results, we take Dau-3 scale function and we use 5-point Gauss-type quadrature rule involving Daubachies scale function. The approximate results together with exact values are displayed in Figure 1. Both the Table 3 and Figure 1 show excellent agreement between approximate and exact results.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Approximate and exact solutions of example 1

TABLE 3. Approximate and exact solutions of example 1

x	Analytical solution	j = 4	j = 5	j = 6
		Approximate solution
0	0	0	0	0
1/8	0.017578	0.018131	0.017660	0.017590
2/8	0.078125	0.078666	0.078209	0.078138
3/8	0.193359	0.193996	0.193461	0.193375
4/8	0.375000	0.375781	0.375124	0.375019
5/8	0.634766	0.635718	0.634916	0.634789
6/8	0.984375	0.985523	0.984555	0.984403
7/8	1.435550	1.436920	1.435760	1.435580

Example 2

Consider the following FIDE¹²

D^{0.15} y (x) - \frac{1}{4} \int_{0}^{x} \frac{y (t)}{{(x - t)}^{\frac{1}{2}}} d t - \frac{1}{7} \int_{0}^{1} e^{x + t} y (t) d t = f (x),

()

with the initial condition

y (0) = 0,

where

f (x) = \frac{Γ (3)}{Γ (2.85)} x^{1.85} - \frac{Γ (2)}{Γ (1.85)} x^{0.85} - \frac{\sqrt{π} Γ (3)}{4 Γ (3.5)} x^{2.5} + \frac{\sqrt{π} Γ (2)}{4 Γ (2.5)} x^{1.5} - \frac{e^{x + 1} - 3 e^{x}}{7} .

The exact solution of this problem is y(x) = x² − x. The approximate results of example 2 for the resolution level j = 4, 5, 6 at the points

x = \frac{ζ}{8} (ζ = 0, 1, 2, . . . ., 7)

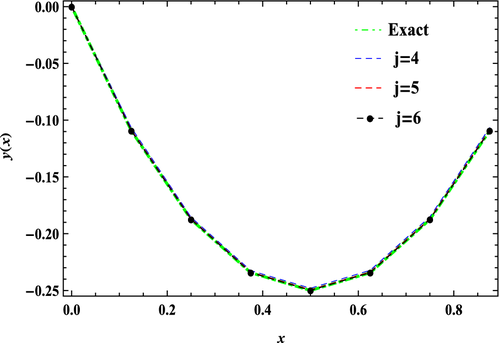
are shown in Table 4 along with corresponding exact values. The calculation is done taking Dau-3 scale function and M = 5. In Figure 2 approximate numerical results and exact results are shown. As in the previous example, here also the Table 4 and Figure 2 show excellent agreement.

TABLE 4. Approximate and exact solutions of example 2

x	Analytical solution	j = 4	j = 5	j = 6
		Approximate solution
0	0	0	0	0
1/8	−0.109375	−0.106636	−0.108771	−0.109235
2/8	−0.187500	−0.185570	−0.187039	−0.187378
3/8	−0.234775	−0.232564	−0.233905	−0.234249
4/8	−0.250000	−0.248064	−0.249493	−0.249864
5/8	−0.234375	−0.232249	−0.233816	−0.234224
6/8	−0.187500	−0.185134	−0.186877	−0.187332
7/8	−0.109375	−0.106724	−0.108676	−0.109186

Example 3

Consider the following FIDE¹¹

D^{α} y (x) - \int_{0}^{x} \frac{y (t)}{{(x - t)}^{\frac{1}{2}}} d t - \int_{0}^{1} (x + s i n t) y (t) d t = f (x),

()

with initial condition

y (0) = 0,

and

f (x) = 2 x - \frac{\sqrt{π} Γ (3)}{Γ (3.5)} x^{2.5} - \frac{1}{3} x - c o s 1 - 2 s i n 1 + 2 .

The exact solution of this problem is y(x) = x² for

α = 1

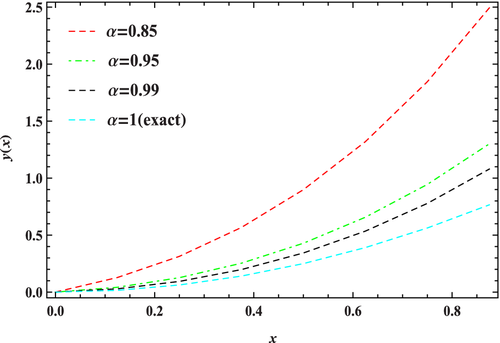
The proposed method is used here to find approximate numerical solutions of Equation (67) at j = 4, 5, 6 for different values of $α (e.g., α = 0.85, 0.95, 0.99)$ . These obtained data are displayed in Table 5. It is observed that the approximate results approach to the exact solution y(x) = x² as $α$ approaches to 1. A large amount of computational error may occurred, if we use the proposed method for $α = 1$ . The reasons for this situation are mentioned in Section 4.1. Figure 3 shows approximate results for different values of $α$ for a particular resolution level (j = 6). The figure shows a good agreement between proposed method and the block pulse method.¹¹

TABLE 5. Approximate solutions of example 3 for different values of

α

		Approximate solution
	x	j = 4	j = 5	j = 6
$α = 0.85$	0	0	0	0
	1/8	0.112945	0.120189	0.128218
	2/8	0.289574	0.301993	0.313809
	3/8	0.533670	0.550261	0.567142
	4/8	0.853351	0.875169	0.898505
	5/8	1.260050	1.288430	1.319820
	6/8	1.767760	1.804240	1.845560
	7/8	2.393540	2.439880	2.493400
$α = 0.95$	0	0	0	0
	1/8	0.043537	0.041757	0.042350
	2/8	0.128188	0.125409	0.126612
	3/8	0.257204	0.252693	0.253495
	4/8	0.434511	0.427714	0.428633
	5/8	0.665486	0.655790	0.656846
	6/8	0.956892	0.943553	0.944764
	7/8	1.317050	1.299150	1.300540
$α = 0.99$	0	0	0	0
	1/8	0.031570	0.028000	0.028700
	2/8	0.098675	0.094359	0.093878
	3/8	0.204922	0.198407	0.197593
	4/8	0.344445	0.875169	0.343201
	5/8	0.549646	0.536764	0.534976
	6/8	0.798021	0.780695	0.778222
	7/8	1.105620	1.082770	1.079440

TABLE 6. Values of

‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2}

for different resolution j

j	Example 1	Example 2	$α = 0.85$	$α = 0.95$	$α = 0.99$
			Example 3
4	1.67697(10⁻¹)	2.32942(10⁻⁴)	4.47105(10⁻¹)	1.28896(10⁻¹)	9.01604(10⁻²)
5	9.29065(10⁻²)	3.21493(10⁻⁵)	2.54939(10⁻¹)	7.07976(10⁻²)	4.91910(10⁻²)
6	4.91481(10⁻²)	4.21763(10⁻⁶)	1.37523(10⁻¹)	3.74053(10⁻²)	2.58997(10⁻²)
7	2.53064(10⁻²)	5.40004(10⁻⁷)	7.16031(10⁻²)	1.92644(10⁻²)	1.33155(10⁻²)
8	1.28440(10⁻²)	6.83182(10⁻⁸)	3.65568(10⁻²)	9.78067(10⁻³)	6.75445(10⁻³)

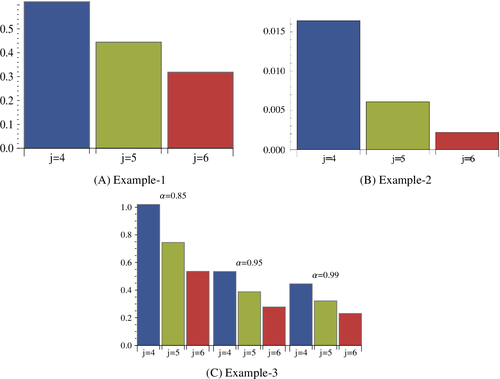
In Table 6, the values of $‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2}$ given by Equation (64) are represented for the examples 1, 2, and 3, respectively, for different values of j. It is observed from Table 6 that the values of $‖ δ y_{j} (x) ‖_{L^{2} [0, 1]}^{2}$ gradually decrease if the resolution level j is gradually increased. $τ = 0.554014, 0.529006, 0.514901$ and $τ = 0.138014, 0.131189$ ,0.128035 are taken to determine the upper bound of L²-norm error $‖ e (x) ‖_{L^{2} [0, 1]}$ for examples 1 and 2, respectively. Three distinct values of $α (α = 0.85, 0.95, 0.99)$ are considered to find approximate numerical solutions for the example 3. For the evaluation of the upper bound of L²-norm error $‖ e (x) ‖_{L^{2} [0, 1]}$ of the example 3, the three sets of $τ$ namely $τ = 0.570199, 0.539435, 0.520663$ ; $τ = 0.549261, 0.528341, 0.515018$ , and $τ = 0.545594, 0.526513, 0.514118$ are used for three distinct values of $α$ mentioned earlier at the resolution level j = 4, 5, 6. The upper bound of L²-norm error $‖ e (x) ‖_{L^{2} [0, 1]}$ together with sup error (for example 1 and 2) are shown in Table 7. Sup errors are calculated taking the maximum absolute error of y(x) at the points $x = \frac{ζ}{8} (ζ = 0, 1, \dots, 7)$ . The upper bound of L²-norm error $‖ e (x) ‖_{L^{2} [0, 1]}$ at the resolution level j = 4, 5, 6 for different values of $α$ for example 3 are shown in Table 8. The bar diagrams of upper bound of L²-norm error $‖ e (x) ‖_{L^{2} [0, 1]}$ are shown in Figure 4 for the examples 1, 2, and 3 to show dependence of the accuracy of the proposed method on the resolution level j. The bar diagrams are self-explanatory.

TABLE 7. Sup error and bound

‖ e (x) ‖_{L^{2} [0, 1]}

	j	Sup error	Bound $‖ e (x) ‖_{L^{2} [0, 1]}$
Example 1	4	1.36935 × 10⁻³	6.13300 × 10⁻¹
	5	2.14625 × 10⁻³	4.44135 × 10⁻¹
	6	3.34970 × 10⁻⁵	3.18301 × 10⁻¹
Example 2	4	2.73919 × 10⁻³	1.64389 × 10⁻²
	5	6.99367 × 10⁻⁴	6.08307 × 10⁻³
	6	1.88892 × 10⁻⁴	2.19930 × 10⁻³

TABLE 8. Bound

‖ e (x) ‖_{L^{2} [0, 1]}

for example 3

j	$α = 0.85$	$α = 0.95$	$α = 0.95$
4	1.01993 × 10⁰	5.34758 × 10⁻¹	5.35634 × 10⁻¹
5	7.45000 × 10⁻¹	3.87432 × 10⁻¹	2.77718 × 10⁻¹
6	5.35634 × 10⁻¹	2.77718 × 10⁻¹	2.30878 × 10⁻¹

7 Conclusion

This paper demonstrates a wavelet-based collocation technique to solve FIDE with weekly singular kernel arising in various mathematical models and simulations of systems and processes. The method illustrated here provides a simple way of obtaining approximate numerical solutions avoiding complicated integrals and complexity of calculations. The wavelet-based collocation technique can also be applied to solve non-linear FIDE with weakly singular kernel. However, the actual method depends on the form of the nonlinearity. The validity and applicability of the method is illustrated through three examples and it appears that the method gives favourable results. The bar diagrams analyse that the bounds of error $‖ e (x) ‖_{L^{2} [0, 1]}$ have the reverse proportional relation with the resolution level j. The convergency rate of the proposed method is comparatively fast for lower fractional order $α$ for a fixed resolution level j. The efficiency in obtaining approximate numerical solutions depends on the choice of resolution level j. The results can be improved by taking larger resolution level j.

Acknowledgements

The authors thank the Reviewers for their comments and suggestions to revise the paper in the present form. Jyotirmoy Mouley acknowledges financial support from University Grants Commission, New Delhi, for the award of research fellowship (File no. 16-9[june2017/2018(NET/CSIR)]).

Biographies

Jyotirmoy Mouley is a research scholar (Senior Research Fellow, UGC, New Delhi, India) of the Department of Applied Mathematics, University of Calcutta, Kolkata, India. He works to find numerical solution of integral and differential equations arising in different field of mathematical physics using bases of different wavelets family. His interest areas of research include Integral equations, Differential equations, Numerical analysis, and Wavelet analysis.
B. N. Mandal is a retired professor in Physics and Applied Mathematics Unit of Indian Statistical Institute, Kolkata. His specialization is in applied mathematics having expertise on water waves, integral equations, integral transforms, differential transforms, numerical analysis, wavelets, inventory and queuing in OR etc. He has published more than 290 research papers in these topics and and also coauthored/edited 10 research monographs.

References

1Zozulya VV, Gonzalez-chi PI. Weakly singular, singular and hyper singular integrals in 3-D elasticity and fracture mechanics. J Chin Inst Eng. 1999; 22: 763-775.
10.1080/02533839.1999.9670512
Web of Science® Google Scholar
2Kythe PK, Puri P. Computatioal Method for Linear Integral Equations. Boston, MA: Birkhauser; 2002.
10.1007/978-1-4612-0101-4
Google Scholar
3Tang BQ, Li XF. Solution of a class of Volterra integral equations with singular and weakly singular kernels. Appl Math Comput. 2008; 199: 406-413.
Web of Science® Google Scholar
4Momani S, Jammel A, Al-Azawi S. Local and global uniqueness theorems on fractional integro differential equation via Bihari's and Gronwall's inequalities. Soochow J Math. 2007; 33: 619-627.
Google Scholar
5Pedas A, Tamme E, Vikerpuur M. Spline collocation for fractional weakly singular integro-differential equations. Appl Numer Math. 2016; 110: 204-214.
10.1016/j.apnum.2016.07.011
Web of Science® Google Scholar
6Nemati S, Sedaghat S, Mohammadi I. A fast numerical algorithm based on the second kind Chebyshev polynomials for fractional integro-differential equation with weakly singular kernels. J Comput Appl Math. 2016; 308: 231-242.
10.1016/j.cam.2016.06.012
Web of Science® Google Scholar
7Yi M, Wang L, Jun H. Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. App. Math Model. 2016; 40: 3422-3437.
10.1016/j.apm.2015.10.009
Web of Science® Google Scholar
8Mokhtary P. Numerical analysis of an operational Jacobi Tau method for fractional weakly singular integro-differential equations. Appl Numer Math. 2017; 121: 52-67.
10.1016/j.apnum.2017.06.010
Web of Science® Google Scholar
9Nemati S, Lima PM. Numerical solution of nonlinear fractional integro-differential equation with weakly singular kernels via a modification of hat functions. Appl Math Comput. 2018; 327: 79-92.
Web of Science® Google Scholar
10Biazar J, Sadri K. Solution of weakly singular fractional integro-differential equations by using a new operatioal approach. J Comput Appl Math. 2019; 352: 453-477.
10.1016/j.cam.2018.12.008
Web of Science® Google Scholar
11Mohammadi F. Fractional integro-differential equation with a weakly singular kernel by using block pulse functions. UPB Sci Bull Ser A. 2017; 79: 57-66.
Google Scholar
12Keshavarz E, Ordokhani Y. A fast numerical algorithm based on the Taylor wavelets for solving fractional integro-differential equations with weakly singular kernels. Math Method Appl Sci. 2019; 42: 4427-4443.
10.1002/mma.5663
Web of Science® Google Scholar
13Panja MM, Mandal BN. Wavelet Based Approximation Schemes for Singular Integral Equations. Boca Raton, FL: CRC Press; 2020.
Google Scholar
14Mouley J, Panja MM, Mandal BN. Numerical solution of an integral equation arising in the problem of cruciform crack using Daubechies scale function. Math Sci. 2020; 14: 21-27.
10.1007/s40096-019-00312-w
Web of Science® Google Scholar
15Kessler BM, Payne GL, Polyzou WW. Notes on wavelets; 2003. arXiv:nucl-th/0305025v2.
Google Scholar
16Panja MM, Mandal BN. Gauss-type quadrature rule with complex nodes and weights for integrals involving Daubechies scale functions and wavelets. J Comput Appl Math. 2015; 290: 609-632.
10.1016/j.cam.2015.05.024
Web of Science® Google Scholar

Citing Literature

All articles

Wavelet-based collocation technique for fractional integro-differential equation with weakly singular kernel

Abstract

1 Introduction

2 Basic preliminaries and notations

2.1 The fractional derivative and integrals

2.2 Collocation method

2.3 Multiscale (wavelet) basis of Daubechies family

3 Method of approximation

4 Evaluation of matrix elements

4.1 Evaluation of $J_{α j}^{(n)} (k^{'}, k)$

4.2 Evalution of $I_{μ j} (k^{'}, k)$

4.3 Evaluation of $Q_{j} (k^{'}, k)$

5 Multiscale approximation and Error estimation

6 Illustrative examples

Example 1

Example 2

Example 3

7 Conclusion

Acknowledgements

Biographies

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Wavelet-based collocation technique for fractional integro-differential equation with weakly singular kernel

Abstract

1 Introduction

2 Basic preliminaries and notations

2.1 The fractional derivative and integrals

2.2 Collocation method

2.3 Multiscale (wavelet) basis of Daubechies family

3 Method of approximation

4 Evaluation of matrix elements

4.1 Evaluation of J α j ( n ) ( k ′ , k )

4.2 Evalution of I μ j ( k ′ , k )

4.3 Evaluation of Q j ( k ′ , k )

5 Multiscale approximation and Error estimation

6 Illustrative examples

Example 1

Example 2

Example 3

7 Conclusion

Acknowledgements

Biographies

References

Citing Literature

Figures

References

Related

Information

4.1 Evaluation of $J_{α j}^{(n)} (k^{'}, k)$

4.2 Evalution of $I_{μ j} (k^{'}, k)$

4.3 Evaluation of $Q_{j} (k^{'}, k)$