Proposition of a new index for projection pursuit in the multiple factor analysis

2.1 Notation

Most low-dimensional projections are approximately normal.^{6, 11} The main appropriate indexes for reduction in dimension d ≥ 1, are described in Tables A1 and A2 (Appendix A).

The optimization of the equation is done by numerical methods, which are traditionally based on the gradient,^{6, 7} or the Newton-Raphson method;^{2, 12} however, they are not appropriate for scenarios above three dimensions.⁸

Other global optimizers have been proposed, for example: TRIVES,¹³ random scanning algorithm,¹⁴ simulated annealing,³ genetic algorithm,¹⁵ and particle swarm optimization.¹⁶

3.1 Generation of samples for the application of multiple factor analysis

In order to assess the performance of the index proposed in Section 3.2, we considered several scenarios that exhibited different degrees of correlation between the variables belonging to each group, and heterogeneity between the groups. To that end, we performed the procedure proposed by Cirillo et al.,¹⁷ in which the samples were generated from normal dependent and heterogeneous populations.

Multivariate observation was specified by vector $\check{X}$, in which each component was given by ${\check{X}}_j={(X_{j1},\dots ,X_{jp})}^T$ for j = 1, … , k, being k the total number of groups and p the number of variables, considering the autoregressive of order 1 correlation structure, $AR(1)$, defined in (3). Each block delimited by dashed lines corresponds to the correlation structure of the samples generated by a normal multivariate distribution with global correlation structure R_b. The global covariance matrix was obtained through (4)

$${\sum }^{\ast }=D^{\frac{1}{2}}{R}_b{D}^{\frac{1}{2}},$$ ()

in which $D^{\frac{1}{2}}$ is a diagonal matrix with the standard deviations of the variables. With these specifications, the multivariate samples from normal dependent populations were generated by ${\check{X}\sim N}_{pk}({\check{\mu }}_{pk},{\sum }^{\ast })$ taking the parametric values defined in (5) and (6).

$${\check{\mu }}_{pk\times 1}=\left[\begin{array}{c}{\tilde{\mu }}_1=0\\ ⋮\\ {\tilde{\mu }}_1=0\end{array}\right]$$ ()

$${\sum }^{\ast }=\left[\begin{array}{ccc}{\sum }_{11}& \dots & {\sum }_{k1}\\ ⋮& \ddots & ⋮\\ {\sum }_{k1}& \dots & {\sum }_{kk}\end{array}\right].$$ ()

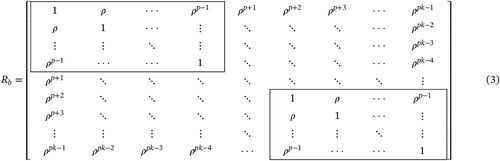
The covariances represented in ${\sum }^{\ast }$ (6) are non-zero, since each element on the diagonal represents the jth covariance matrix of the group of variables indexed by j = 1, … , k.

3.2 Proposed index for use with MFA

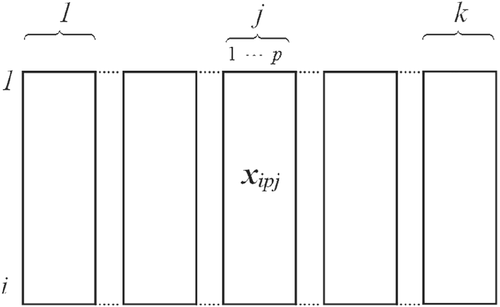
The multivariate sample $X_{n\times m}=[X_{n\times p}^1\left|\cdots \right|X_{n\times p}^j\left|\cdots \right|X_{n\times p}^k]$ was composed of groups of variables k in n observations in each group, with m = pk. This way, the observation x_ipj being i = 1, … , n and j = 1, … , k is identified as the ith observation in the jth group to which the pth variable belongs, as suggested by the layout of Figure 1.

It is worth noting that the equality in (10) is due to the comparison of the results with different dimensions. For example, considering matrices X_n × m and ${\tilde{X}}_{n\times s}$, when applying the MFA technique, we will obtain the respective eigenvector matrices V and $\tilde{V}$. The similarities between the groups are expressed in Tables 3 and 4, respectively.

The numerical optimization to find a plane that maximized the index (16) was obtained by a modification in the grand tour algorithm (Section 3.3) using the simulated annealing method proposed by Cook et al.,¹⁹ so that groups of variables could be considered in line with the MFA.

The validation of the proposed index (16) was performed by comparing the degree of agreement in validating the reduction of projection pursuit in two dimensions for each group of variables. For this purpose, we performed 1,000 Monte Carlo simulations. Scripts were developed using the R software²⁰ and a grand tour alternated with a simulated annealing optimization adapted for MFA (Section 3.3), with the specifications of 5e³ iteractions, cooling =0.95, eps = 1e⁻⁴, and half =30 to compute the indexes mentioned in Section 2, according to the scenarios described in Table 2 and using non-spherical data in the simulations with reduction of two dimensions in the data of each group.

3.3 Projection pursuit algorithm for the MFA technique

Input: $X_{n\times pk}=[X_{n\times p}^1\left|\cdots \right|X_{n\times p}^j\left|\cdots \right|X_{n\times p}^k]$ matrix with k groups of variables.

 p: number of variables in the group j.

 n: number of observations.

 Maxiter: maximum number of iterations.

 Cooling: initial value of the cooling parameter in the range $(0,1).$

 Half: number of steps without changing Cooling.

 Eps: approximation accuracy for Cooling.

  for j = 1 : k do

  Generate random initial projection A_a, with d < p

   Perform linear transformation $T_0=X^j{\times A}_a$ for the jth group.

  Calculate the search index of the initial projection, ${PI}_{MF}^0(T_0).$

  Perform h = 0, Cooling = 0.95, Half = 30, Eps = 1e⁻⁴ and i = 1.

  while(i < Maxiter and Cooling > Eps) do

    Generate a new random projection A_i.

    Then, generate a new projection $A_i^{\ast }=A_a+Cooling\times A_i$.

    Perform $A_z=interpolation(A_a,A_i^{\ast })$, interpolation from the projection A_a

    until projection $A_i^{\ast }$.

    Perform linear transformation $T_i=X^j{\times A}_z$, for jth group.

    Calculate ${PI}_{MF}^i(T_i)$.

    if ${PI}_{MF}^i<{PI}_{MF}^0$ do

         Perform A_a = A_z, ${PI}_{MF}^0={PI}_{MF}^i$

    else

         Perform h + =1

    end if

    if h = Half then

         Perform $Cooling=Cooling\ast 0.9$ and h = 0

    end if

    Perform i + =1

  end while

  Perform ${\tilde{X}}_{n\times d}^j=T_i$, which represents the matrix with the reduced dimension

  of the jth group

  end for

  The new matrix with k groups of variables with reduced dimensions will be

  represented by: ${\tilde{X}}_{n\times dk}=[{\tilde{X}}_{n\times d}^1\left|\cdots \right|{\tilde{X}}_{n\times d}^j\left|\cdots \right|{\tilde{X}}_{n\times d}^k].$

Output: The MFA technique is applied to groups formed in ${\tilde{X}}_{n\times dk}$.

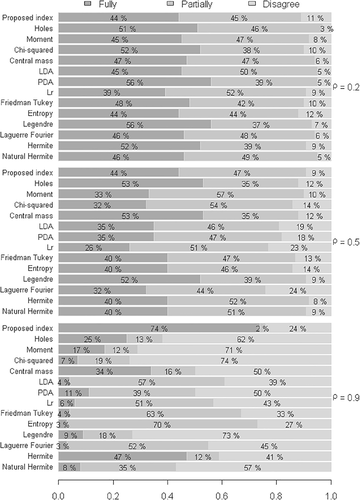
4.1 Evaluation of the proposed index with respect to the heterogeneity between the groups

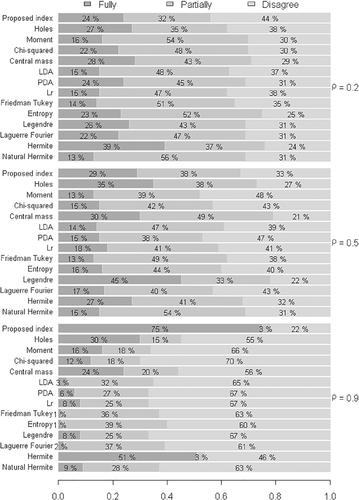
The results illustrated in Figure 2 indicate that the proposed index initially exhibited a high discordance rate in comparison to the other indexes, when considering a weak degree of correlation between the variables $(\rho =0.2)$. However, as the degree of correlation increased, this rate was reduced. This way, maintaining a strong degree of correlation between the variables $(\rho =0.9)$, the proposed index resulted in low disagreement and promising results with respect to agreement with the others. It is worth noting that the simulated data were non-spherical, a condition that usually undermines the applicability of the proposed indexes.

In view of the above, in order to compare the validation of the index for the same scenarios, even though the degree of heterogeneity between the groups was increased $(\delta =8)$, the results illustrated in Figure 3 were compared with the condition of low heterogeneity $(\delta =2)$ illustrated in Figure 2.

The results illustrated in Figure 3 practically confirmed the same behavior of the indexes with respect to the degree of correlation between the variables and the degrees of agreement and disagreement between the indexes. Virtually, any difference results from error oscillation in the Monte Carlo method. However, a result that should be highlighted was the strong degree of correlation $(\rho =0.9)$. In this context, we observed that the proposed index exhibited a high degree of agreement when the samples were simulated for a low degree of heterogeneity $(\delta =2)$, with a percentage close to 75%. When the index was increased to $(\delta =8)$, it exhibited considerable improvement, with a percentage of agreement close to 81%.

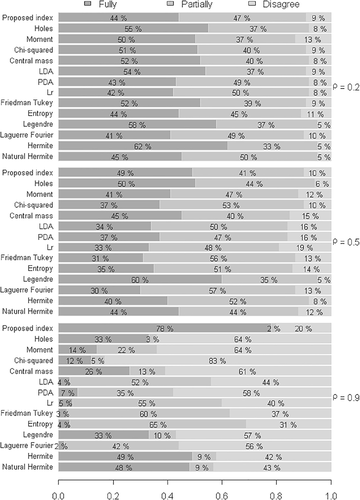
4.2 Evaluation of the proposed index with respect to the increase in the number of groups

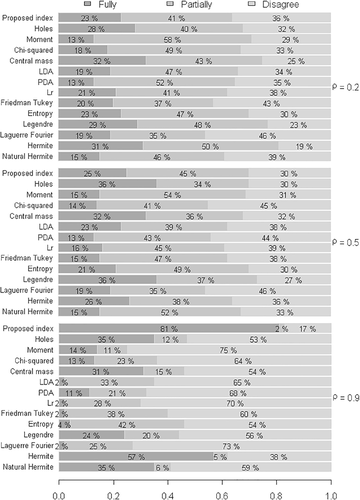
Compared with the results illustrated in Figure 2, in which low heterogeneity was considered between groups and groups $(k=7)$, it is noted in Figure 4 that, with the same configurations, the increase in the number of groups $(k=10)$ confirmed that the degrees of agreement and disagreement of the proposed index were approximately equal when $(\rho =0.9)$. Therefore, there is statistical evidence that the index yields promising results when the variables are strongly correlated, regardless of the dimension of the group.

Considering the high heterogeneity between the groups $(\delta =8)$, the increase in the number of groups $(k=10)$, in general terms, did not affect the performance of the indexes. Figure 5 shows that the same behavior of the indexes occurred regarding the degree of correlation and the agreement rate in comparison with the competing indexes.

It should be emphasized that in all simulated scenarios, in conditions of poor $(\rho =0.2)$ and moderate correlation $(\rho =0.5),$ the proposed index exhibited a reduction in the disagreement rate with respect to its competitors. In this context, there is evidence to affirm that, on average, all indexes are affected by the increase in the number of groups. This way, it can be affirmed that the occurrence of these results does not prevent the application of the indexes evaluated in the present study, that is, projection pursuit applied in MFA.

5.1 Use of the MFA technique

We simulated three groups of variables (Table 5). The data of each group were generated according to the methodology described in Section 3.1, using the parameters $\rho =0.9$ and $\delta =1$.

The explanations of the principal components described in Table 6 were obtained applying the MFA technique,¹⁸ with scripts elaborated using the R software and the MVar package.²¹

The inertia of the groups of variables are described in Table 7.

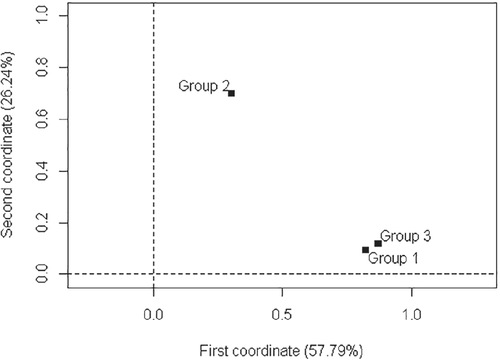
With respect to the first principal component, Table 7 shows that groups 1 and 3 exhibited strong similarity between them (0.8240 and 0.8718, respectively) and group 2 differed from the others. Regarding the second component, it can be affirmed that groups 1 and 3 were similarly weak, and group 2 remained original. Other analyzes could have been performed with the other components; however, as full explanation had already been given by the first component—with the greatest explanation (57.79%)—no other explanation was necessary besides that given by the first principal component.

From the inertias obtained in the groups (Table 7), aiming at a better interpretation, a chart of inertia (Figure 6) was elaborated showing that there was strong relationship between groups 1 and 3 with respect to the first component, thus confirming the originality of group 2.

5.2 Use of the MFA technique with dimension reduction performing projection pursuit with the proposed index

We used matrix X_6 × 10 illustrated in Table 5 of Section 5.1. We obtained the projection matrices for each group with the projection indexes (Table 8) by applying projection pursuit with the proposed new index presented by Equation (16), and new algorithm presented in Section 3.3.

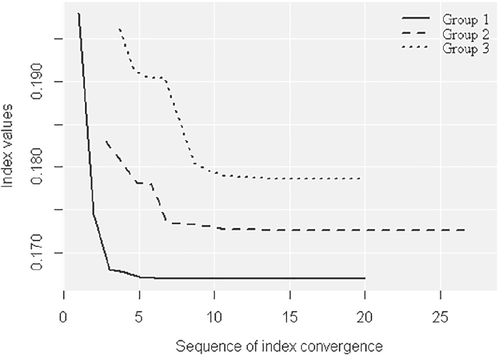
Figure 7 shows the convergence of the new index for each group of variables in the numerical optimizations.

When we applied the projection matrices in the groups in X_6 × 10, we obtained the data shown in Table 9, which represent the data with reduced dimensions in two dimensions for each set X^j, so that matrix X_6 × 10 will be represented by the new matrix ${\tilde{X}}_{6\times 6}$.

We applied the MFA technique in the new groups of variables (Table 9). The explanations of the principal components are given in Table 10.

The inertias of groups of variables with reduced dimensions are described in Table 11.

The same observations made in Table 7, which deal with the similarities of groups of variables with original dimensions, apply to Table 11. Regarding the first principal component, groups 1 and 3 exhibited strong similarity between them, and group 2 differed from the others.

Aiming at a better interpretation, the chart of inertia illustrated in Figure 8 was again elaborated from the inertias of the groups shown in Table 11. There was strong relationship between groups 1 and 3, again confirming the originality of group 2.

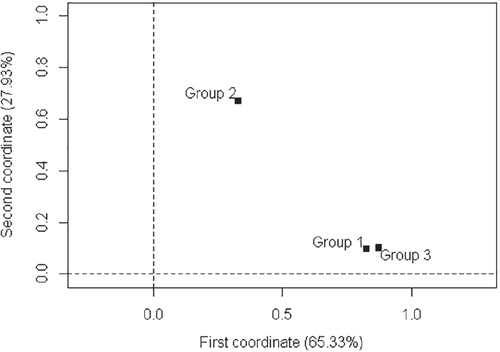
As can be observed, the results of the similarities in data with reduced dimensions produced the same results than the data with original dimensions. This fact demonstrates the efficiency of the proposed new index with application in MFA using high-dimensional data.