Interaction of A chains and fibrillary seeds studied by all-atom molecular dynamics simulations
Funding information: Alberta Prion Research Institute, 201700016
Abstract
We apply all-atom molecular dynamics simulations to investigate interactions of amyloid beta (A) fibril seeds with natively disordered A chains, a process associated with the onset of Alzheimer's disease. The simulations captured attachment of A chains to the fibrils suggesting an onset of both fibril's elongation and secondary nucleation, with a stronger affinity of attachment leading to elongation. Choice of fibril's model appears important for the propensity to recruit A chains from solution and retain them adsorbed. Nuclear magnetic resonance-based and cryo-electron microscopy derived models of A fibrils exhibited significant differences in the interaction with individual A chains, as well as in structural and dynamical stability in solution.
1 INTRODUCTION
Numerous biological functions that proteins perform exploit their unique ability to adopt specific three-dimensional (3D) conformations. Native conformations of proteins determine their stability and interactions with other components. However, under conditions that are not yet fully understood, protein chains may misfold into abnormal configurations.1, 2 Such misfolded constructs can trigger a cascade of self-replicating misfolding events producing -sheet rich amyloid fibrils, which accumulate in the brain and other tissues.3-5 Realization of this resulted in a discovery of previously unknown mechanism of neurodegenerative diseases.1, 2 Amyloid fibrils were found in patients with Parkinson's, Huntington's, or Alzheimer's diseases, and their formation is associated with neurodegeneration.3-5
In particular, Alzheimer's disease (AD) is linked to aggregation of amyloid beta (A) peptide.6 A peptides originate from proteolytic cleavage of the amyloid precursor protein by -secretase and -secretase enzymes.7 Depending on the exact cleavage site, this produces peptides of usually 38–43 amino acids in length. Out of these, A and A are the most abundant species, and A is believed to be the most pathogenic.8 Native A peptides are commonly classified as intrinsically disordered proteins. As such, at normal conditions they adopt a continuum of disordered conformations ranging from partially structured to completely random coil-like organization.9
The self-replicating process of protein misfolding has been investigated intensely. It has been found that -sheet rich amyloid species, once they have nucleated, give rise to fibrils composed of -strands oriented perpendicularly to the fiblil's axis. These fibrils provide molecular templates for further misfolding.4, 10, 11 Two mechanisms of template-driven misfolding are commonly distinguished. One is merely an increase of existing fibrils in length through attachment of additional protein material to fibril edges, commonly denoted to as elongation. Dissociation or fragmentation of fibrils is also possible. Furthermore, presence of fibrils can catalyze the formation of similar misfolded copies, or new “secondary” fibrils, through a positive-feedback reaction loop also known as the secondary nucleation mechanism.12-14 It is believed that secondary nucleation occurs at lateral surfaces of the fibril.14, 15 Evidence has emerged that relatively small aggregates (oligomers) that arise in the process of misfolding and aggregation might be responsible for the AD progression.16, 17 Despite the intense effort, it is not yet clear what exactly chains of molecular events lead to pathogenic transformations, and what is the structure and morphology of the corresponding intermediate states, oligomers, and other misfolded species.
Molecular dynamics (MD) simulations offer unique capabilities to investigate the misfolding and aggregation processes at the atomistic level in a time-dependent manner.9, 18-21 The ability of MD simulations to predict molecular motion in such details that often is not achievable otherwise is crucial. Selected milestones include the identification of the dock-and-lock mechanism for the A fibril elongation,22 as well as elucidation of the role of solvation23-25 and hydrogen bonding,9, 18 to name a few. In agreement with results of earlier kinetic modeling,26, 27 MD simulations28 have indicated that aggregation of short disordered peptides might be driven by a competition of hydrophobic collapse and hydrogen bonding. MD simulations of A fibril elongation have consistently confirmed the important role of hydrogen bonding in a buildup of -sheet structures.22, 25 However, attempts to model secondary nucleation through the deposition of A monomers onto lateral surfaces of fibrillary filaments seem to suggest a prevalence of hydrophobic collapse resulting in disordered morphologies of deposited chains.29-31
Further computational studies are needed to better understand the specific molecular mechanisms of misfolding and aggregation of A peptide. Recently, this challenging task has been facilitated by the advent of two high-resolution full-length A fibril structures. The 2NAO structure was determined from solution nuclear magnetic resonance (NMR)32, 33 measurements. Moreover, due to recent progress in cryo-electron microscopy (EM) imaging techniques, nearly atomic resolution has been achieved for the 5OQV fibril model from cryo-EM34 experiments. In distinction from earlier fibril models that contained various fragments of the A peptide, each of the 2NAO and 5OQV models expresses entire 42-residue A chains. One can expect that this improvement would allow more accurate predictions of molecular events that involve such fibrils. In this work we use all-atom MD simulations to investigate interactions of both NMR-based and cryo-EM derived A fibril models with unstructured monomeric A chains in water, and analyze molecular mechanisms that potentially could indicate the onset of fibril elongation, secondary nucleation, and dissociation.
2 MATERIALS AND METHODS
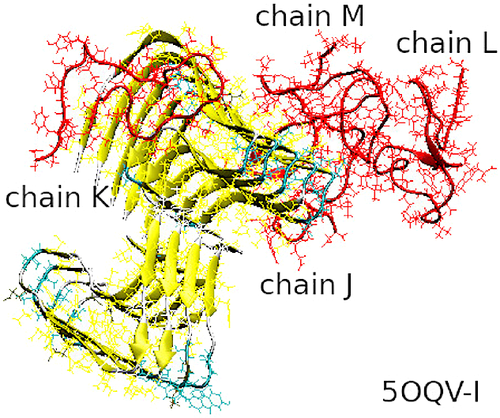
To study in detail the interaction between unstructured A peptides with the fibrillary seeds, we have done all-atom MD simulations using the GROMACS-5.0.7 package.35, 36 As starting structures for the fibrillary seeds, we used hexamers from NMR-based model32, 33 (PDB ID 2NAO, Figure 1(A)) and nonamers from cryo-EM model34 (PDB ID 5OQV, Figure 1(B)). Both models consist of two domains originating from two filaments in a fibril. In model 2NAO the two domains contain three S-shaped chains each, which are denoted as chains A, B, C and D, E, F, respectively (Figure 1(A)). In model 5OQV the chains adopt a staggered architecture with screw symmetry relative the fibril axis, resulting in five LS-shaped chains in one domain and four similarly shaped chains in the other one. Following the notation adopted in the original protein data bank (PDB) file,34 the chains from the two filaments of model 5OQV are labeled as shown in Figure 1(B). Because the original 2NAO and 5OQV structures were obtained for pH of 7.4 and 2.0, respectively, we used the PROPKA server37 to determine the protonation states compatible with physiological pH for both models. This resulted in three excess negative charges for each peptide chain, which was offset by adding Na+ counterions in accordance with standard procedures.
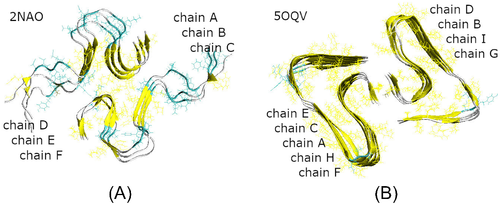
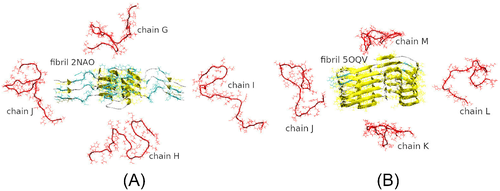
Our model systems consisted of a 2NAO or 5OQV fibril model and four randomly positioned unstructured monomeric A chains in explicit water (Figure 2). The models of four A monomers 1DAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVVIA42 were prepared by extracting chains A–D from the 2NAO and 5OQV PDB files, respectively. Their protonation state was adjusted as described above; the chains models were minimized, equilibrated, and simulated with NPT ensemble for 10 ns each in order to achieve unstructured conformations typical of free A momomers. Then Accelrys VS38 and VMD39 packages were used to randomly position these monomeric chains around fibril fragment 2NAO or 5OQV, at a distance of at least 22 Å from each other and from the fibril. Fibril fragment was positioned in the center of a cubic simulation box and aligned with the Z axis. Six A units of the 2NAO fibril were labeled A–F, and four free monomeric chains were labeled G–J (Figure 2(A)). Nine A units of the 5OQV fibril were labeled A–I, and the four free monomeric chains were labeled J–M (Figure 2(B)).
The AMBER99SB-ILDN forcefield40 was used for all protein atoms. In vacuo minimizations of single chains, fibril fragments, and composite systems using the steepest descent algorithm for energy were followed by addition of single point charge extended water molecules and counterions to electro-neutralize the systems. Subsequent solvent equilibrations involved decreasing position restraints on nonhydrogen protein atoms, as well as heating with the Berendsen thermostats and NVT-equilibrations. Six independent MD simulations were carried out for each of the two composite systems to collect sufficient statistics. The simulations employed similar starting coordinates of atoms and independently random-generated initial atom velocities using the Maxwell distributions. The six simulation trajectories were labeled I, II, III, … VI. In addition, simulations for each of the two fibrils models alone also were conducted.
Production MD simulations, as well as the last equilibration step, were conducted at a temperature of 310 K and pressure of 1 atm. We used isotropic pressure coupling (NPT ensemble); Verlet cut-off neighbor searching; Particle-Mesh Ewald treatment of electrostatics with a 14 Å cut-off; twin-range scheme with a 14 Å cut-off for van der Waals interactions; and bond lengths restrained with the linear constant solver algorithm with a fourth order of expansion. The V-rescale scheme was used for temperature coupling, and the Parrinello–Rahman scheme for pressure coupling with reference coordinates scaled via the center of mass. MD simulations were performed for at least 200 ns for the 12 composite systems, and for 250 ns for two fibril systems. 2 fs time steps were used, and position snapshots were saved every 20 fs in order to analyze the essential collective dynamics (ECD).
Structural analysis of the trajectories, such as assessment of the secondary structure, calculations of the number of hydrogen bonds, and solvent accessible areas, was done using the GROMACS package scripts36 and the VMD package.39 For graphical representation, the VMD, UCSF Chimera41 and Accelrys VS38 packages were utilized.
The ECD method42-46 was employed for dynamical analysis of the aggregation of fibrils and monomeric chains. The ECD method relies upon the statistical-mechanical framework42, 43 according to which a macromolecule can be described by generalized Langevin equations with essential collective coordinates identified as principal eigenvectors of a covariance matrix from principal component analysis of MD trajectories. In the ECD method an all-atom projected image of the protein is constructed in a multidimensional space of the essential collective coordinates, such that each atom is represented as a point (atom-image). The ECD theory proves42, 43 that such projected image represents the degree of dynamical correlation between the atoms. Two atom-images located close to each other indicate a strongly correlated motion of the corresponding atoms regardless their proximity in tertiary structure of the protein, whereas distant atom-images correspond to a relatively independent motion. The concept of projected atom-images allows calculating a suite of simple descriptors for dynamical coupling in a protein.42-46 It has been demonstrated43 that such descriptors represent persistent correlations of atomic motion, making exhaustive sampling of MD conformations unnecessary for accurate predictions. The method successfully passed validation against NMR-derived data that represent longer timescales than used in the MD sampling,42-45, 47 and has been applied extensively to analyze collective dynamics of proteins.45-48 In this work, we calculate pair correlation maps that explicitly visualize the distances between pairs of atom-images in the systems of interest. For this purpose, we do the principal component analysis and determine 20 principal eigenvectors for multiple subnanosecond trajectory segments. Earlier it has been demonstrated42-46 that this allows removing high-frequency random noise, while spanning approximately 90% or more of total displacement. Then the pair correlations are computed for each subnanosecond segment. Equations used to calculate the pair correlations can be found in several publications.45, 46, 48 Finally, the calculated pair correlations are averaged over the last 20 ns of the simulations.
3 RESULTS AND DISCUSSION
We started with verifying the stability of fibril models 2NAO and 5OQV during MD simulations in water at a pH of 7.4. Figure 3(A,B) show snapshots of the two models after 250 ns of the simulations, and Figure 3(C,D) illustrate the corresponding evolution of secondary structure. Both fibril fragments have retained most of their secondary structure as well as the gross 3D shape during the simulations. However, solution NMR-based fragment 2NAO developed certain twisting, as it could be seen from comparison of Figures 3(A) and 1(A). By contrast, the shape of cryo-EM based fragment 5OQV remained very stable during the simulations. The 2NAO model shows lower population of -sheets (approximately 35% after 250 ns) than the 5OQV model (approximately 60% after 250 ns). This difference originates largely from disordered N-terminal part of A chains in model 2NAO, especially in the region of residues 1–13 (Figure 3(E)). In Figures 1(A) and 3(A) this region appears as loose “external ends” at two sides of the 2NAO fibril, suggesting relative instability of this model. By contrast, the N-terminal region is well structured in model 5OQV (Figures 1(B), 3(B,F)).
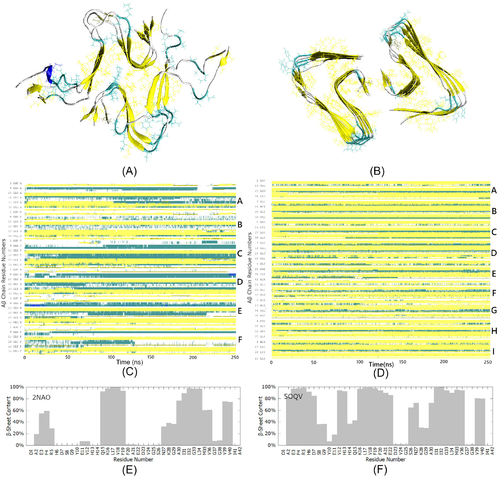
Figure 4 gives examples of composite systems containing fibril fragment 2NAO or 5OQV and four monomeric A chains after 200 ns of MD simulations. In Figure 4(A,C,E,G), A chains that initially were free are highlighted in red color. The corresponding ECD pair correlation maps for C atoms, averaged over the last 20 ns of the 200 ns trajectories, are presented in Figure 4(B,D,F,H). In the correlation maps, pair correlations between C atoms are color-coded such that strong dynamical coupling is shown by red and yellow colors, and relatively independent motion is indicated by blue color.
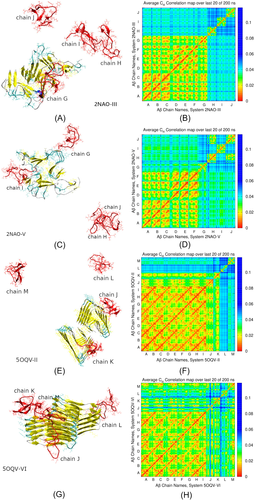
In particular, Figure 4(A) depicts threading of an initially free A chain G along an edge of the fibril in system 2NAO-III. This is accompanied by a partial alignment with -strands of the fibril and buildup of -sheet content in the threading chain. Occupancy of -sheet content around residues 16–17 and 31–32 of chain G increased from 0% initially to 60%–62% in the threaded state. The other three chains H, I, and J remain in the solution. As one could expect, the corresponding ECD pair correlation map in Figure 4(B) shows pronounced dynamic correlations across chains A–F that form the fibril, as well as between the attached chain G and the fibril. N-terminus, region V24-K28, and extensive C-terminal part of chain G exhibit the strongest correlations with chains of the fibril. By contrast, chains H, I, and J do not show strong correlations with the fibril, or between the monomers. In system 2NAO-V (Figure 4(C)) two monomeric chains, G and I, have attached to lateral sides of the fibril, whereas chains J and H formed a globular dimer that remained in the solution. According to the pair correlation map in Figure 4(D), the J–H dimer exhibits strong correlations across the two chains. However, dynamic coupling between chains G or I and the fibril is relatively weak. Only N-terminus of chain G developed pronounced dynamical correlations with chains D, E, and F of the fibril. Correlations of chain I are even less pronounced, although this chain developed contacts with the fibril through residues I31-V36.
Figure 4(E,G) illustrate examples for systems 5OQV-II and 5OQV-VI, respectively, which contain the fibril fragment 5OQV. In system 5OQV-II (Figure 4(E)) chains J and K have attached, respectively, to an edge and lateral side of the fibril where they developed extensive -content, whereas chains L and M remained in solution. As it is clear from the corresponding correlation map (Figure 4(F)), both chains J and K that attached to the fibril developed strong correlations with it. In system 5OQV-VI depicted in Figure 4(G), all four A chains J,K,L, and M have formed a complex with the fibril by 200 ns of the simulation. Out of these, chains J and M initially landed on an edge of the fibril; however, chain J subsequently moved and attached to lateral side. Chain L attached to opposite side of the fibril, whereas chain K attached to chain M. The pair correlation map in Figure 4(H) indicates that the entire system comprising the fibril and four A chains is strongly intercorrelated.
Table 1 summarizes molecular events observed in all 12 MD simulations. In all the systems, attachment of initially monomeric A chains to the fibril was observed during 200 ns. Alignment (threading) of A chains along an edge of the fibril, which is believed to be a precursor of fibril elongation, occurred in systems 2NAO-III (chain G in Figure 4(A)) and 5OQV-I (chain K in Figure 5). In system 2NAO-III the threading was accompanied by a buildup of -sheet content in the threading chain. In system 5OQV-I the threading was less robust. Residues 1–11 and 38–42 of chain K detached from the fibril and attached to each other during subsequent simulation. Generally, A chains tend to adopt collapsed unstructured conformations when landing on an edge of a fibril, as found for chain K in Figure 4(E), or chain M in Figures 4(G) and 5. Deposition of A chains on lateral sides of the fibrils was observed frequently (Table 1). Although attachment to fibril's sides might indicate an onset of secondary nucleation of a twin fibrillary filament, we have not observed pronounced alignment of attached chains with -strands at side surfaces of the fibril. For example, chains G and I in Figure 4(C), chain J in Figure 4(E), or chain L in Figure 4(G) adopt largely unstructured conformations upon attaching to a side of the fibril. However, unexpectedly we have observed partial alignment of deposited chains along or fibril's axis, such as for chain J in Figure 4(G). In ECD pair correlation maps, the strongest dynamic coupling is observed for threading of A chains along an edge of the fibril, as shown in Figure 4(B). By contrast, attachment of chains to sides of fibril 2NAO is relatively loose (Figure 4(D)). However, for system 5OQV, attachment to both edges and sides of the fibril tends to produce strong correlations of deposited chains with the fibril (Figure 4(F,H)), and is frequently accompanied by a buildup of extensive -sheet content, despite a lack of alignment with structural elements of the fibril. Attachment of A chains to both edges of the fibrils and their sides often involves N-termini and residues H13-N28, and occasionally C-terminal groups.
| System | Aggregates' sizea | Monomers' aggregation in solution | Attachment to edge or side of fibril | Comments |
|---|---|---|---|---|
| 2NAO-I | 6+4 | Yes | Both | 8 ns, chain G binds to I; 18 ns, J binds to dimer GI; 116 ns, trimer GIJ binds to fibril, then G detaches and attaches to H; 150 ns, dimer GH binds to dimer IJ already in complex with the fibril. |
| 2NAO-II | 6+4 | Yes | Side | 2 ns, chain G binds to I; 7 ns, dimer GI binds to fibril; 44 ns, H binds to GI already in complex with the fibril; 139 ns, J binds to GHI-fibril complex. |
| 2NAO-III | 6+1,2,1 | Yes | Edge | 11 ns, chain G threads over edge of fibril; 198 ns, I binds to H; J remains free. |
| 2NAO-IV | 6+1+1,2 | Yes | Both | 3 ns, chain H binds to fibril's edge; 9 ns, J binds to fibril's side; 72 ns, G binds to I. |
| 2NAO-V | 6+1+1,2 | Yes | Both | 16 ns, chain H binds to J; 182 ns, G binds to fibril's side; 188 ns, I binds to fibril's edge. |
| 2NAO-VI | 6+2+2 | Yes | Both | 1 ns, chain J binds to fibril; 6 ns, N-terminus of fibril's chain D detaches; 7 ns, I binds to fibril; 10 ns N terminus of fibril's chain C detaches; 12ns, N-terminus of fibril's chain A detaches; 14 ns, G binds to I; 16 ns, detached N-terminus of A rebinds in different position, while N-terminus of fibril's chain C detaches; 18 ns, J detaches; 34 ns, detached N-terminus of C rebinds in different position, and continues shifting thereafter; 36 ns, detached N-terminus of D rebinds in different position, and continues shifting thereafter; 87 ns, H binds to J; 105 ns, more residues of chain D detach; 145 ns, dimer HJ binds to fibril. |
| 5OQV-I | 9+3+1 | No | Both | 2 ns, chain J binds to fibril's side; 6 ns, M binds to fibril's edge; 12 ns, J binds to M; 94 ns, L binds to dimer JM; 155 ns, K threads over opposite edge of the fibril; 165 ns, N- and C-termini of chain K detach from fibril and attach to each other; central region of K remains attached to the fibril. |
| 5OQV-II | 9+1+1,1,1 | No | Both | 4 ns, chain J binds to fibril's side; 4 ns, K binds to fibril's edge; chains L and M remain free. |
| 5OQV-III | 9+1+2,1 | Yes | Both | 1 ns, chain M binds to fibril's edge; 58 ns, K binds to L; 147 ns, dimer KL binds to fibril's side; J remains free. |
| 5OQV-IV | 9+2+1+1 | Weak | Both | 3 ns, chain J binds to fibril's side; 6 ns, M binds to fibril's edge; 33 ns, J binds to M; 32 ns K binds to L; 42 ns, dimer KL dissociates; 66 ns, L binds fibril's side, 170 ns K binds to opposite side; 190 ns, K wraps over fibril's edge. |
| 5OQV-V | 9+1+3 | Yes | Side | 18 ns, K binds to fibril's side; 21 ns, M binds to different side; 50 ns, J binds to L; 195 ns, dimer JL binds to M. |
| 5OQV-VI | 9+3+1 | No | Both | 0 ns M binds to fibril's edge; 5 ns J binds to the edge; 17 ns J moves to fibril's side and binds to M; 16 ns, K binds to M; 48 ns, L binds fibril's side. |
- Note: Included are the numbers of monomeric chains that have attached to the fibril and/or aggregated (second column); whether or not monomers have aggregated before or instead binding to the fibril (third column); the location at an edge or lateral side of the fibril where monomers or their aggregates have attached (fourth column); and selected details of the MD trajectories.
- Abbreviation: MD, molecular dynamics.
- a In second column a 6 represents a 2NAO hexamer, and a 9 represents a 5OQV nonamer. A 1 denotes a monomeric A chain, whereas 2, 3, and 4 denote, respectively, dimers, trimers, and tetramers formed by these chains. Attachment of one, two, or more chains to a fibril is indicated by a “+” sign, for example, 6+1 or 6+1+1, and so forth. Attachment of an aggregate of two, three, or four chains to a fibril is represented by 6+2, 6+4, 9+3, and so forth. Chains or their aggregates that have remained in solution are marked by commas; for example, a 6+1,1 means that a monomer remains in solution, and a 6+1,2 means that a dimer remains in solution.
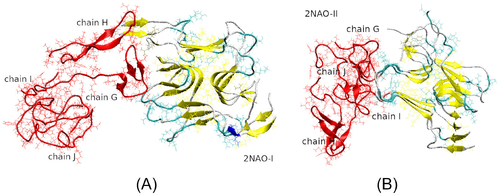
In composite systems with fibril 2NAO, monomeric chains tend to form unstructured globular aggregates. For example, in systems 2NAO-V, chains H and J formed a dimer that remained in solution and did not attach to the fibril during 200 ns (Figure 4(C) and Table 1). Similarly in system 2NAO-IV, chains G and I formed a dimer that remained in solution. However, in systems 2NAO-I and 2NAO-II dimeric or trimeric aggregates did bind to the fibril. This binding was followed by partial dissociation and restructuring of the aggregates, and eventually resulted in formation of quasi-globular tetrameric oligomers attached to the fibril (Figure 6(A,B) and Table 1). In systems containing fibril 5OQV, aggregation of monomers in solution was less frequent (Table 1). When such aggregation occurred, it was followed by attachment of the aggregates to the fibril. In addition, we have observed migration of deposited chains over fibril's surface, which sometimes was accompanied by aggregation of the adsorbed chains. For example, in system 5OQV-I shown in Figure 5, shortly after equilibration chains J and M landed on fibril's side and edge, respectively. After 12 ns these two chains formed a dimer while remaining on the fibril's surface, and later at 95 ns one more chain, L, attached to the JM dimer. The resulting trimeric aggregate JLM can be seen in Figure 5. The tendency to form unstructured aggregates is compatible with similar behaviors observed from MD simulations of A in water48 and after adsorption of A onto side surfaces of fibrillary filaments.29, 30
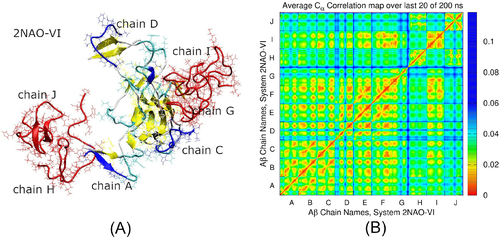
As it is evident from Figures 4-6, both fibril models 2NAO and 5OQV retain the gross 3D shape in most composite systems during MD simulations. A notable exception is system 2NAO-VI, where significant restructuring of the fibril occurred. After 6 ns of the simulation, a relatively loose N-terminal region 1–5 of fibril's chain D detached from the fibril, which was followed by detachment of residues 6–8 later at 105 ns. Meanwhile chains J and I bound to the opposite side of the fibril at 1 and 7 ns, respectively. Interaction with chain J caused partial detachment of fibril's chain A (residues 1–5) at 12 ns. This was preceded by detachment of N-terminus of chain C (residues 1–11), although this detachment was not caused by direct interaction with monomeric chains. Rather, loss of structural integrity of the fibril might play a role. The detached N-termini of chains A, C, and D each rebound to different spots in the fibril at 16, 34, and 36 ns, respectively, and continued shifting thereafter. This was accompanied by changes in aggregation status of chains G, H, and J, as outlined in Table 1. Structure of system 2NAO-VI after 200 ns is depicted in Figure 7(A), where misplaced parts of chains A, C, and D are featured in blue color. The three chains are significantly displaced. In particular, chains A and D have changed positions relative to their respective neighbor chains, whereas chain C developed connections with chains D, E, and F from different filament. Interestingly, this restructuring was accompanied by formation of new network of hydrogen bonding between misplaced chains and the rest of the fibril. For example, N-terminal region 1–14 of chain C had six hydrogen bonds with chain B initially. In the course of relocation these bonds were broken and replaced by three bonds with fibril's chain F and three bonds with initially free chain I. Region 15–42 of chain C has remained bound to the fibril. Together, the newly formed and remaining bonds have resulted in fairly robust pair correlations across five out of six fibril's chains in Figure 7(B). Despite significant change in positions of chains A and C , they still exhibit pronounced dynamical correlations with each other and with chain B, as well as with chains E and F from different filament. Only chain D remains relatively loosely correlated in comparison with other chains of the restructured fibril.
Comparative analysis of fibril's robustness and their propensity to recruit A chains from solution reveals significant differences between models 2NAO and 5OQV. As shown in Figure 3(A,E) and discussed earlier, in model 2NAO N-terminal regions of A chains are relatively loosely structured and develop less -sheet content in comparison with model 5OQV. In addition, from comparison of ECD correlation maps in Figure 4(B,D,F,H) it is evident that intrafibril correlations between chains that belong to different filaments are significantly stronger in model 5OQV than in model 2NAO. Interestingly, model 5OQV exhibits a greater robustness than model 2NAO even despite the change of protonation state that we did to make the model compatible with a pH of 7.4 instead of 2.0. We also note that the only system where partial dissociation and restructuring of the fibril occurred is 2NAO-VI. From the results listed in Table 1 it follows that fibril 5OQV exhibits a stronger propensity to recruit A chains from solution and retain them adsorbed. Out of six simulations for each fibril model, after 200 ns three or more A chains remained bound to the fibril in three 2NAO systems and in five 5OQV systems. However, the presence of fibril 2NAO results in more frequent aggregation of A chains in solution.
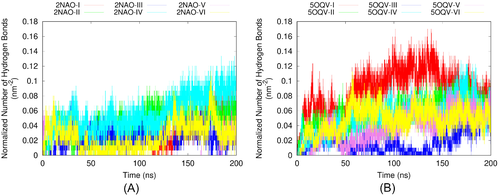
In order to reach a greater insight into the differences between the two fibril models, we have calculated the number of hydrogen bonds between the fibril and adsorbed A chains in each system during the MD simulations. Complementary to the information contained in the ECD correlation maps, the numbers of hydrogen bonds quantify robustness of binding between selected molecules. To take into account the difference in size of the two fibril models, we have normalized the numbers of hydrogen bonds per initial solvent-accessible surface areas of 2NAO and 5OQV models (of 149.45 and 195.05 nm2, respectively). The dependencies of the normalized number of hydrogen bonds on MD simulation time for each system are given in Figure 8(A,B). In all systems buildup of hydrogen bonding starts early in the simulation and progresses extensively. Although due to dynamical nature of the systems the number of hydrogen bonds fluctuates significantly, it is clear that in systems with 5OQV fibril A chains bind to the fibril faster and in average develop more bonds than in systems with 2NAO fibril. After 100 ns, the average number of hydrogen bonds between initially free A chains and the fibril is 1.5–2 times greater in most systems with 5OQV fibril than in systems with 2NAO fibril. The tendency of hydrogen bonding to continuously increase with time indicates that we are observing early stages of aggregation in most of the systems considered.
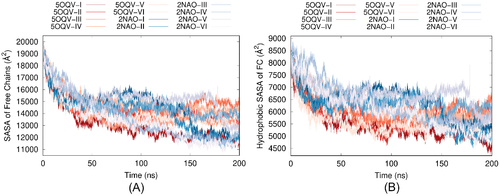
Finally, we have calculated the evolution of solvent accessible surface area (SASA) of initially free A chains in the composite systems during MD simulations. Changes in total SASA of A chains are representative of their aggregation status, whereas solvent exposure of hydrophobic residues is an important indicator of structural vulnerability of proteins in water. Figure 9(A) depicts the time dependencies of total SASA of the four A chains in all 12 systems. According to the figure, total SASA decreases by 30%–40% over the first 50 ns of the simulations in the presence of either fibril model. Although A chains develop more hydrogen bonds with fibril 5OQV than with fibril 2NAO, the decrease in total solvent exposure is close in average. Slight differences between the systems with two fibril models can be seen in Figure 9(B), where SASA of hydrophobic residues in the four A chains is shown. At the beginning of the MD simulations and up to approximately 100 ns, hydrophobic SASA tends to be somewhat lower in systems with fibril 5OQV, because the chains bind to fibril 5OQV quicker. Over the last 100 ns the difference becomes less pronounced, although general decrease in hydrophobic SASA after 200 ns is still slightly stronger for 5OQV systems than for 2NAO systems. However, the difference in SASA is less pronounced than that in hydrogen bonding. The relative uniformity of the evolution of solvent exposure of free A chains regardless pronounced differences in the number of hydrogen bonds formed between these chains and the fibril may indicate a prevalence of hydrophobic collapse of A chains as leading mechanism of aggregation in the systems considered.
4 CONCLUSIONS
All-atom MD simulations offer unique opportunity to see how molecular events unfold during peptide aggregation. In this work, 200 ns long MD simulations of composite systems containing free monomeric A chains and recently published fibril models 2NAO and 5OQV in water captured attachment of A chains to both fibril models. Attachment to both edges and sides of the fibrils was observed, which may indicate an onset of fibril elongation or secondary nucleation, respectively.
A chains tend to adopt unstructured collapsed conformations both in solution and upon binding to the fibril. When they land onto the fibril, the attachment often involves N-termini and residues H13-N28, and occasionally C-terminal groups. Partial alignment with -strands of the fibril was observed through threading of the chains along fibril's edges. In addition, such threading produced the strongest dynamical coupling between the chains and the fibril in ECD correlation maps. When landing on lateral surfaces of the fibrils, in most cases A chains remain in collapsed conformations; often they migrate and form aggregates when remaining adsorbed. Robust dynamical coupling was observed for side binding with model 5OQV but not 2NAO. Although A chains attach more often to sides of fibrils than to edges, a greater dynamical stability and more pronounced alignment with -strands of the fibril for chains attached to fibril's edges may suggest a greater affinity involved in molecular events that lead to fibril elongation in comparison to secondary nucleation in the systems considered.
Choice of fibril's model has emerged as an important factor for A chains' aggregation. Our results indicate that fibril 5OQV exhibits a stronger propensity to recruit A chains from solution and retain them adsorbed, whereas the presence of fibril 2NAO results in more frequent aggregation of A chains in solution. In composite systems with 5OQV fibril A chains bind to the fibril faster and develop significantly more hydrogen bonds than in systems with 2NAO fibril. Attachment of A chains to both edges and sides of fibril 5NAO tends to produce strong correlations of deposited chains with the fibril, and is frequently accompanied by a buildup of extensive -sheet content, despite a lack of alignment with structural elements of the fibril.
Remarkably, fibril model 5OQV also shows a greater structural and dynamical stability and more abundant -sheet content in comparison with model 2NAO. This refers especially to N-terminal region of the fibril, which is significantly better structured in model 5OQV. It is interesting that the stability of model 5OQV appears unaffected by the change of its protonation state that we did to match the physiological pH. Although the robustness of model 5OQV might be partially due to more peptides contained in the model, the fact that model 5OQV has fewer unstructured regions than 2NAO seems to be more important. In one of composite systems we observed partial dissociation and restructuring of fibril 2NAO. The latter seems to be largely due to initially unstructured N-termini of the chains. Combined with fewer number of the peptides, this had led to the N-terminal instability. One can expect that in a multispecies solution, such structures as 5OQV might serve as preferential fibrillization seeds, whereas 2NAO-like structures would rather tend to dissociate.
Unlike the pronounced difference in the aptitude of fibril models 2NAO and 5OQV to develop hydrogen bonds with adsorbed A chains, the dependence of solvent-accessible surface area of the chains on the simulation time is relatively uniform across the various systems. This may indicate a prevalence of hydrophobic collapse of A chains as leading mechanism of aggregation in the systems considered. From a methodical perspective, this highlights the importance of combining complementary analytical methods to investigate early stages of A aggregation in MD simulations.
Although the simulations have captured attachment of A chains to the fibrils, complete alignment of newly attached chains could not be achieved in the course of 200 ns. Longer simulations are required to describe the processes of fibril elongation and secondary nucleation in their entirety. A challenge is that the processes are stochastic in nature and may involve multiple attachment-desorption events accompanied by restructuring of the fibril. Moreover, frequent landing of A chains on lateral surfaces of the fibril followed by formation of quasi-globular oligomers when remaining at the surface, may result in restructuring and alignment of these oligomers after sufficiently long simulation times. Extensions of MD protocols to include various levels of coarse-graining49 might offer additional dimensions to address more advanced stages of protein misfolding and aggregation in the future.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Holger Wille and his group members for stimulating discussions. Molecular images were created using the VMD package 37. The simulations were carried out using the Compute Canada facilities. Support of the work by the Alberta Prion Research Institute, project 201700016, is gratefully acknowledged.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
AUTHOR CONTRIBUTIONS
Lyudmyla Dorosh and Maria Stepanova designed the methods. Lyudmyla Dorosh and Min Wu performed the simulations under the supervision of Maria Stepanova. Lyudmyla Dorosh and Maria Stepanova analyzed the data and wrote the article. Maria Stepanova provided resources for the work. All the authors read and approved the final version of the article.
Biographies
Dr. Lyudmyla Dorosh is currently working as a Research Associate in the Department of Electrical and Computer Engineering at the University of Alberta, Edmonton, Canada. She obtained her PhD from the Institute for Condensed Matter Physics, National Academy of Sciences of Ukraine, in 2006. Her research interests include, but are not limited to, the following areas: data analysis, in silico modeling, molecular dynamics simulations, essential dynamics analysis, amyloid formation, drug design, solvation effects, and free energy calculations.
Dr. Min Wu is currently a postdoctoral fellow at in the Department of Electrical and Computer Engineering, at the University of Alberta. She received her B.E. degrees in Biological Engineering from Beijing Institute of Technology and her PhD degree in Materials Engineering from the University of Alberta. Her research is focused on computational and biological science with the purpose to understand the properties of protein folding and unfolding, and as well as disease-related protein oligomerization.
Dr. Maria Stepanova is an Adjunct Professor in the Department of Electrical and Computer Engineering at the University of Alberta. After graduating from the Faculty of Physics at the Lomonosov Moscow State University, Russia, in 1984, she received her PhD from the National Center for Surface Research, Russia, in 1992, and her DrSci degree from the Higher Attestation Commission, Russia, in 1998. Dr. Stepanova's crossdisciplinary research agenda includes theoretical understanding and prediction of the mechanisms that cause formation of complex structures at micro and nanoscales. In particular, she conducts modeling studies on the molecular mechanisms of misfolding and aggregation of proteins related to diseases.




