Poom Kumam, KMUTT Fixed Point Research Laboratory, Room SCL 802 Fixed Point Laboratory, Science Laboratory Building, Department of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, ThrungKhru, Bangkok 10140, Thailand.

Email: [email protected]

Search for more papers by this author

Saeed Islam,

Saeed Islam

Faculty of Mathematics & Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

Informetrics Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam

Search for more papers by this author

Poom Kumam,

Corresponding Author

Poom Kumam

[email protected]

KMUTT Fixed Point Research Laboratory, Room SCL 802 Fixed Point Laboratory, Science Laboratory Building, Department of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), Bangkok, Thailand

Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan

Correspondence

Zahir Shah, Department of Mathematics, University of Lakki Marwat, Lakki Marwat 28420, Khyber Pakhtunkhwa, Pakistan.

Email: [email protected]

Search for more papers by this author

Muhammad Jawad,

Muhammad Jawad

Department of Mathematics, Abdul Wali Khan University, Mardan, Pakistan

Search for more papers by this author

Anwar Saeed,

Anwar Saeed

orcid.org/0000-0003-1566-6457

Department of Mathematics, Abdul Wali Khan University, Mardan, Pakistan

Search for more papers by this author

Zahir Shah,

Corresponding Author

Zahir Shah

[email protected]

orcid.org/0000-0002-5539-4225

Department of Mathematics, University of Lakki Marwat, Lakki Marwat, Pakistan

Correspondence

Zahir Shah, Department of Mathematics, University of Lakki Marwat, Lakki Marwat 28420, Khyber Pakhtunkhwa, Pakistan.

Email: [email protected]

Search for more papers by this author

Saeed Islam,

Saeed Islam

Faculty of Mathematics & Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

Informetrics Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam

Search for more papers by this author

Poom Kumam,

Corresponding Author

Poom Kumam

[email protected]

Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan

Correspondence

Zahir Shah, Department of Mathematics, University of Lakki Marwat, Lakki Marwat 28420, Khyber Pakhtunkhwa, Pakistan.

Email: [email protected]

Search for more papers by this author

First published: 19 November 2020

https://doi.org/10.1002/cmm4.1136

Funding information: Center of Excellence in Theoretical and Computational Science

Share a link

Email
Wechat
Bluesky

Abstract

In this article, the study of magnetohydrodynamics Darcy-Forchheimer flow is carried out. Viscous dissipation and thermal radiation are also deliberated for the flow system over a stretching and porous surface. Buongiorno model has been utilized to elaborate thermophoresis and Brownian dispersion impacts. The physical quantities such as viscosity, density, and specific heat play a key role in liquid flow behavior. The modeled equations are transformed to nonlinear ordinary differential equations and then solved by semi-analytical technique HAM. It is found in this assessment that expanding estimations of the magnetic parameter builds Lorentz force and henceforth decreases the velocity profile. Moreover, velocity is also a reducing function of porosity and inertial parameters. The temperature of nanofluid diminishes with enhancement in the Prandtl number and porosity parameter while it increases with Brownian motion, radiation, thermophoretic parameters, and Brinkman number. The concentration profile is a growing function of the thermophoretic parameter and a reducing function of the Brownian motion parameter and Lewis number.

1 INTRODUCTION

The researchers at current are concerned in analyzing the liquid flow through a permeable medium which has been broadly applied in assembling and technological processes. This area has attained a significant concentration of current researchers since it has been established very common in several applications of present technology like geothermal energy utilization, nuclear-based repositories, porous bearings, fermentation processes, heat exchangers, insulation of gas cooled reactors, crude oil production, ground water pollution, recovery systems, and so on. Porous surface is a continuous solid surface full of void or pores such as rocks (limestone), sandstone, cloth sponge, rye bread, foamed plastic, catalyst pellets and gall bladder with stones, and so on. The porosity is the fraction of pore spaces to the total volume of the surface. Nature is full of porous media, many of them are manmade. There are many applications of a porous medium in engineering and industry such as seepage of water in river beds, mass and heat transfer in packed bed reactor and drying of permeable materials in the textile industry, and so on. Since by Darcy Law, flow is dependent linearly upon gravitational force and pressure gradient. When the medium is closed packed (low permeability) then this law provides a motion equation for Newtonian fluids in porous surface with low Reynolds number. But whenever pores in the medium are large with low distribution then the porous medium will have large voids in it that result in viscous shear in adding to Darcy opposition. The Forchheimer term was included by Muskat¹ afterward. Pal and Mondal² discussed the Darcy-Forchheimer model past a permeable surface with fickle viscosity. In this study, the authors highlighted that the concentration distribution of nanoparticles reduces with an augmentation of the electric field parameter. Ganesh et al³ investigated Dracy-Forchheimer flow for magnetohydrodynamics (MHD) nanoparticles over stretching/shrinking medium by using second-order slip. Hayat et al⁴ investigated Drachy-Forchceimer flow by using Cattaneo-Christo heat flux.

Muhammad et al⁵ investigated the Darcy-Forchheimer model in the revised form for a Maxwell nanofluid subjected to convective boundary conditions. As the main outcome of their study, they highlighted that temperature and concentration of nanoparticles upsurge with an augmentation in the porosity factor. Vaidyanathan et al⁶ investigated Soret driven Ferro thermohaline convective flow in the present as well the absence of a porous surface. Kim⁷ discussed stability analysis on the onset of Soret driven motion for suspended nanoparticles. Hemalatha^{8, 9} studied rotation effect on Soret driven Ferro thermohaline convective motion of dust particles in the presence and absence of porous sheet. Rosenswig¹⁰ discussed the viscosity of fluid flow using a magnetic field. Rudraiah et al¹¹ discussed the MHD convective flow of fluid using heat generation. They analyze this discussion numerically by considering various isothermal boundary combinations. Shivakumara et al¹¹ investigated onset convection flow for the sparsely packed porous surface. Jawad et al^12-14 carried out an extensive study for various types of flow in a permeable medium. Gul et al¹⁵ have defined the stream of the two sorts of nanoliquids, GO-W and GO-EG, which were examined for the intensification of heat. Numerical and hypothetical studies were approved under the result of Marangoni convection. Hayat et al¹⁶ have designated Darcy-Forchheimer flow of magnetohydrodynamic Jeffrey nanoliquid confined by non-linear extending area with movable viscosity. Heat transmission is considered with melting heat and heat absorption/generation.

Kausar et al¹⁷ discussed boundary layer flow for Darcy-Brinkman porous surface by considering slip effects and porous dissipation. Madhu et al¹⁸ examined the MHD boundary layer movement with heat transmission using a Siskonanofluid model over a stretched sheet with thermal radiations. Recently, due to sharp development in the modern industry, scientists and researchers are provoked to search such techniques and methods that are used for enhancement of heat transmission in heat exchanger equipment. To fulfill these requirements, scientists and researchers developed a new type of fluid named nanofluid and are used for commercial and industrial applications. This type of fluid is prepared by suspending nanoparticles in some base fluid. Experiments have shown that a combination of nanoparticles with base fluid enhances the coefficient of heat transmission of nanofluids. Applications of such fluids are one of the innovative heat transmission enhancements with great efficacy as studied and discussed by the researchers.^19-22 Khanafer and Vafai carried out a critical synthesis for the thermophysical characteristics of nanofluids. Mital²³ analyzed analytically the transmission of heat and pumping of power of nanofluid by introducing microchannel fluid flow. Hung et al²⁴ investigated heat transmission for micro-channel heat sinks by applying various types of nanoliquids.

Akbari et al²⁵ discussed laminar flow and heat transmission for water and aluminum oxide (Al₂O₃) nanoliquid. In this study, the authors have used different nanoparticles volume fractions in a 3-D micro-channel of rectangular shaped. They also investigated an enhancement in heat transfer by using rough surfaces in the channel. Behnampour et al²⁶examined a statistical study for heat transmission and nanofluid flow in micro channels by using various shaped ribs such as triangle, rectangle, and trapezoidal. In this study, the authors highlighted that the triangular-shaped rib has the finest thermal enactment assessment criteria estimations, while the rectangular shaped rib creates the record variations in streamlines with small heat transmission estimations. Gravandyan et al²⁷ discussed numerical simulation for laminar heat transmission of nanofluid flow by using a 2-D rectangular shaped micro-channel. In this study, the authors used water/TiO₂ nanofluid as a working fluid and observed that increasing nanoparticles (TiO₂) results in augmentation of heat transmission, performance evaluation criteria, and pressure drop. They also highlighted in this study that the volume fraction of nanoparticles (TiO₂) affected the friction factor.

MHD is the investigation of the elements of such liquids which are electrically led, for example, Fluid Metals, Plasmas, and Electrolytes, and so on. It was presented first by Alfven.²⁸ Ishak et al²⁹ supported a numerical exploration for MHD flow of liquid with heat transmission past a stretched cylinder. In this study, the authors solved the modeled equations numerically by using Keller-box-method. Hayat et al³⁰ talked about the entropy age of the MHD stream for nanoparticles past a non-straight extended medium. In this examination, they researched nano-concentration and heat by compelling utilizing the Brownian movement alongside thermophoresis impact. They additionally settled that stream is unequivocally limited by the magnetic impact. Farooq et al³¹ talked about MHD flow for Maxwell liquid utilizing nanoparticles past an extended surface. Kumar et al³² depicted the MHD and synthetically responding impacts of 3-D non-Newtonian liquid flow past a permeable material. Lahmar et al³³ have considered the variable thermal conductivity and the presence of tending magnetic field effects on heat transmission and liquid flow of squeezing unsteady nanoliquid flow. The accentuations on the three-dimensional Casson nanofluid flow over a slender sheet in permeable layers by considering the thermophoresis and Brownian movement impact was discussed by Durgaprasad et al.³⁴ Ganga et al³⁵ planned the effect of heat generation/absorption on MHD nanoliquid boundary layer flow of a nanofluid over a vertical plate used the Buongiorno model.

The novelty of the current examination is to analyze additionally the thermal radiation impact on Darcy-Brinkman porous medium. Also, we analyze additionally the impact of MHD on the flow. In extra we also incorporate the influence of Forchheimer characteristic past an extending permeable sheet. The viscous dissipation influence is also kept in mind during work. The modeled equations are changed to a set of nonlinear ordinary differential equations (ODEs) and are then solved by utilizing the semi-analytical technique HAM.

2 MATHEMATICAL FORMULATION

Consider 2-D thermally conducted nanofluid flow on an extending sheet. Assume the surface is porous and nanofluid past this surface flow under the influences of thermal radiation and viscous dispersal is also concomitant in this flow. The lines of radiation are orthogonal to the flow path of the fluid. Also we applied the magnetic field whose lines are parallel to the radiation direction. The impact of Brownian and thermophoretic are also concomitant during the flow. Two forces, equal in magnitude and reverse in direction are applied to the flow system in order to widen the sheet in direction of x - axis that also keeps origin as fixed and produces a stretching velocity U = αx along x-axis. Temperature and concentration at the surface of the sheet are T_w, C_w separately whileT_∞, C_∞ are temperature and concentration respectively the free stream (Figure 1).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Geometry of flow problem

Using these assumptions equation the governing equations of the motion of the taken nanofluid in the stated geometry as^{15, 17, 18}:

\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,

()

u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = ν \frac{\partial^{2} u}{\partial y^{2}} - \frac{μ_{nf} ϵ^{2}}{ρ_{nf} K^{*}} u - \frac{σ_{nf} β_{0}^{2}}{ρ_{nf}} u - \frac{C_{b} ϵ}{\sqrt{K}} u^{2},

()

\begin{array}{l} u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = α_{nf} \frac{\partial^{2} T}{\partial y^{2}} + τ [D_{b} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y} + \frac{D_{t}}{T_{\infty}} {(\frac{\partial T}{\partial y})}^{2}] \\ - \frac{ϵ^{2}}{{(ρ C_{p})}_{nf}} [μ_{e} {(\frac{\partial u}{\partial y})}^{2} + \frac{μ_{nf}}{K^{*}} u^{2}] - \frac{1}{{(ρ C_{p})}_{nf}} \frac{\partial q_{r}}{\partial y}, \end{array}

()

u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} = D_{b} \frac{\partial^{2} C}{\partial y^{2}} + \frac{D_{t}}{T_{\infty}} \frac{\partial^{2} T}{\partial y^{2}} .

()

Subjected B.Cs are

\begin{array}{l} u = U = α x, v = 0, T = T_{w}, D_{b} \frac{\partial C}{\partial y} + \frac{D_{t}}{T_{\infty}} \frac{\partial T}{\partial y} = 0 at y = 0, \\ u \to 0, T \to T_{\infty}, C \to C_{\infty} at y \to \infty, \end{array}

()

Above D_b, D_t are Brownian and thermophoretic diffusion coefficients respectively, α_nf is thermal diffusivity, while B₀ is intensity of magnetic field. The value of radiative heat flux is stated as¹⁷:

q_{r} = - \frac{4 σ_{1}}{3 χ} \frac{\partial T^{4}}{\partial y}

()

The value of T⁴ is approximated as¹⁷:

T^{4} = 4 T_{\infty}^{4} T - 3 T_{\infty}^{4} .

()

In light of Equation (7) Equation (6) can be written as.¹⁷

\frac{\partial q_{r}}{\partial y} = - \frac{16 σ_{1} T_{\infty}^{3}}{3 χ} \frac{\partial^{2} T}{\partial y^{2}} .

()

Group of similarity transformation is selected as¹⁷:

\begin{array}{l} ξ = \sqrt{\frac{α}{ν}} y, u = ax f^{'} (ξ), v = - \sqrt{α ν} f (ξ), \\ θ (ξ) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}, ϕ (ξ) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}} . \end{array}

()

Using local similarity transformations given in Equation (9) to Equations (2)–(4) transformed to

f^{‴} - (k_{1} + M) f^{'} - (1 + F_{1}) {f^{'}}^{2} + f f^{″} = 0,

()

\frac{1}{\Pr} (1 + \frac{3}{4} Rd) θ^{″} + N_{b} θ^{'} ϕ^{'} + N_{t} {θ^{'}}^{2} + Ec (γ f^{″} + k_{2} {f^{'}}^{2}) + f θ^{'} = 0,

()

ϕ^{″} - L_{e} \Pr f ϕ^{'} + \frac{N_{t}}{N_{t}} θ^{″} = 0,

()

B.Cs after employing transformation given in Equations (9) to (5) we get the transformed form

\begin{array}{l} f^{'} = 1, f = 0, θ = 1, N_{b} ϕ^{'} + N_{t} θ^{'} = 0 at ξ = 0, \\ f^{'} \to 0, θ \to 0, ϕ \to 0 at ξ \to \infty . \end{array}

()

In the above Equations (10)–(12) some parameters are involved which are further described as $M = \frac{σ_{nf} β_{0}^{0} x}{ρ_{nf} α_{nf}}$ Magnetic parameter, $\Pr = \frac{{(ρ c_{p})}_{nf} x ν_{nf}}{α_{nf}}$ Prandtl number, $Rd = \frac{4 σ_{1} T_{\infty}^{3}}{k χ}$ is radiation parameter, $N_{b} = \frac{τ D_{b} Δ C}{x ν_{nf}}$ is the Brownian motion constraint, $L_{e} = \frac{α_{nf}}{D_{b}}$ is Lewis number, $N_{t} = \frac{τ D_{t} Δ T}{T_{\infty} x ν_{nf}}$ is thermophoresis parameter and $F_{1} = C_{b} ϵ / \sqrt{K}$ is the inertial parameter, $k_{1} = \frac{ϵ^{2} μ_{e} x}{ρ_{nf} α_{nf} K^{*}}$ is porosity parameter, $γ = \frac{ϵ^{2} μ_{e} x}{ρ_{nf} α_{nf}}$ is Brinkman viscosity number, and $Ec = \frac{α_{nf}}{{(C_{p})}_{nf} Δ T}$ is Eckert number.

S_f Skin friction coefficient, Nu Nusselt number, and Sh Sherwood number are stated as

S_{f} = \frac{μ}{ρ U_{s}^{2}} {(\frac{\partial u}{\partial y})}_{y = 0}, Nu = \frac{x}{Δ T} {(\frac{\partial T}{\partial y})}_{y = 0}, Sh = \frac{x}{Δ C} {(\frac{\partial C}{\partial y})}_{y = 0} .

()

In non-dimensional form we have

S_{f} {Re}_{x}^{1 / 2} = f^{″} (0), Nu {Re}_{x}^{1 / 2} = - θ^{'} (0), Sh {Re}_{x}^{1 / 2} = - ϕ^{'} (0)

()

3 SOLUTION METHOD

We adopted the HAM method to solve the current problem given in Equations (10)–(12) with boundary conditions given in Equation (13). Most of the mathematical problems in nature are either highly nonlinear or very intricate to solve and even sometimes it is very difficult to define the exact solution. In order to overcome such problems one need to use an appropriate technique. HAM is one of such technique to determine solution for such kind of problems. For this purpose mathematica software is used. It can be useful to any nonlinear ODEs without constructing use of discretization or linearization. It is also free from the size of embedding parameter. In this technique the control on the region of convergence totally lies with user of the technique. The derivation of the model equations using HAM is given below.

L_{\overset{⌢}{f}} (\overset{⌢}{f}) = {\overset{⌢}{f}}^{‴}, L_{\overset{⌢}{θ}} (\overset{⌢}{θ}) = {\overset{⌢}{θ}}^{″}, L_{\overset{⌢}{ϕ}} (\overset{⌢}{ϕ}) = {\overset{⌢}{ϕ}}^{″},

()

Linear operators

L_{\overset{⌢}{f}}, L_{\overset{⌢}{θ}} and L_{\overset{⌢}{ϕ}}

are signified as

L_{\overset{⌢}{f}} (e_{1} + e_{2} ξ + e_{3} ξ^{2}) = 0, L_{\overset{⌢}{θ}} (e_{4} + e_{5} ξ) = 0, L_{\overset{⌢}{ϕ}} (e_{6} + e_{7} ξ) = 0,

()

The consistent non-linear operatives are rationally considered as

N_{\overset{⌢}{f}}, N_{\overset{⌢}{θ}} and N_{\overset{⌢}{ϕ}}

and identify in system:

N_{\overset{⌢}{f}} [\overset{⌢}{f} (ξ; ζ)] = {\overset{⌢}{f}}_{ξ ξ ξ} - (k_{1} + M) {\overset{⌢}{f}}_{ξ} - (1 + F_{1}) {\overset{⌢}{f}}_{ξ}^{2} + {\overset{⌢}{f} \overset{⌢}{f}}_{ξ ξ}

()

N_{\overset{⌢}{θ}} [\overset{⌢}{f} (ξ; ζ), \overset{⌢}{θ} (ξ; ζ), \overset{⌢}{ϕ} (ξ; ζ)] = \frac{1}{\Pr} (1 + \frac{3}{4} Rd) {\overset{⌢}{θ}}_{ξ ξ} + N_{b} {\overset{⌢}{ϕ}}_{ξ} {\overset{⌢}{θ}}_{ξ} + N_{t} {\overset{⌢}{θ}}_{ξ}^{2} + Ec (γ {\overset{⌢}{f}}_{ξ ξ} + k_{1} {\overset{⌢}{f}}_{ξ}^{2}) + f {\overset{⌢}{θ}}_{ξ}

()

N_{\overset{⌢}{ϕ}} [\overset{⌢}{ϕ} (ξ; ζ), \overset{⌢}{θ} (ξ; ζ)] = {\overset{⌢}{ϕ}}_{ξ ξ} - L_{e} \Pr \overset{⌢}{f} {\overset{⌢}{ϕ}}_{ξ} + \frac{N_{t}}{N_{b}} {\overset{⌢}{θ}}_{ξ ξ}

()

For Equations (18)–(20) the 0th-order system is written as

(1 - ζ) L_{\overset{⌢}{f}} [\overset{⌢}{f} (ξ; ζ) - {\overset{⌢}{f}}_{0} (ξ)] = p ℏ_{\overset{⌢}{f}} N_{\overset{⌢}{f}} [\overset{⌢}{f} (ξ; ζ)]

()

(1 - ζ) L_{\overset{⌢}{θ}} [\overset{⌢}{θ} (ξ; ζ) - {\overset{⌢}{θ}}_{0} (ξ)] = p ℏ_{\overset{⌢}{θ}} N_{\overset{⌢}{θ}} [\overset{⌢}{f} (ξ; ζ), \overset{⌢}{θ} (ξ; ζ), \overset{⌢}{ϕ} (ξ, ζ)]

()

(1 - ζ) L_{\overset{⌢}{ϕ}} [\overset{⌢}{ϕ} (ξ; ζ) - {\overset{⌢}{ϕ}}_{0} (ξ)] = p ℏ_{\overset{⌢}{ϕ}} N_{\overset{⌢}{ϕ}} [\overset{⌢}{ϕ} (ξ; ζ), \overset{⌢}{θ} (ξ; ζ)]

()

The BCs transformed as:

\begin{array}{l} {\frac{\partial \overset{⌢}{f} (ξ; ζ)}{\partial ξ}|}_{ξ = 0} = 1, {\overset{⌢}{f} (ξ; ζ) |}_{ξ = 0} = 0, {\overset{⌢}{θ} (ξ; ζ) |}_{ξ = 0} = 1, {N_{b} \frac{\partial \overset{⌢}{ϕ} (ξ; ζ)}{\partial ξ}|}_{ξ = 0} + {N_{t} \frac{\partial \overset{⌢}{θ} (ξ; ζ)}{\partial ξ}|}_{ξ = 0} = 0 \\ {\frac{\partial \overset{⌢}{f} (ξ; ζ)}{\partial ξ}|}_{ξ = \infty} = 0, {\overset{⌢}{θ} (ξ; ζ) |}_{ξ = \infty} = 0, {\overset{⌢}{ϕ} (ξ; ζ) |}_{ξ = \infty} = 0 . \end{array}

()

Here the implanting parameter is represented by ζ ∈ [0, 1], to control the convergence of the problem solution we used the convergence parameter

ℏ_{\overset{⌢}{f}}

ℏ_{\overset{⌢}{θ}}

, and

ℏ_{\overset{⌢}{ϕ}}

. When ζ = 0 and ζ = 1 we have:

\overset{⌢}{f} (ξ; 1) = \overset{⌢}{f} (ξ), \overset{⌢}{θ} (ξ; 1) = \overset{⌢}{θ} (ξ), \overset{⌢}{ϕ} (ξ; 1) = \overset{⌢}{ϕ} (ξ),

()

Expand the

\overset{⌢}{f} (ξ ζ), \overset{⌢}{θ} (ξ ζ)

and

\overset{⌢}{ϕ} (ξ ζ)

through Taylor's series for ζ = 0

\begin{array}{l} \overset{⌢}{f} (ξ; ζ) = {\overset{⌢}{f}}_{0} (ξ) + \sum_{n = 1}^{\infty} {\overset{⌢}{f}}_{n} (ξ) ζ^{n} \\ \overset{⌢}{θ} (ξ; ζ) = {\overset{⌢}{θ}}_{0} (ξ) + \sum_{n = 1}^{\infty} {\overset{⌢}{θ}}_{n} (ξ) ζ^{n} \\ \overset{⌢}{ϕ} (ξ; ζ) = {\overset{⌢}{ϕ}}_{0} (ξ) + \sum_{n = 1}^{\infty} {\overset{⌢}{ϕ}}_{n} (ξ) ζ^{n} \end{array}

()

{\overset{⌢}{f}}_{n} (ξ) = {\frac{1}{n!} \frac{\partial \overset{⌢}{f} (ξ; ζ)}{\partial ξ}|}_{p = 0}, {\overset{⌢}{θ}}_{n} (ξ) = {\frac{1}{n!} \frac{\partial \overset{⌢}{θ} (ξ; ζ)}{\partial ξ}|}_{p = 0}, {\overset{⌢}{ϕ}}_{n} (ξ) = {\frac{1}{n!} \frac{\partial \overset{⌢}{ϕ} (ξ; ζ)}{\partial ξ}|}_{p = 0} .

()

While BCs are:

\begin{array}{l} f^{'} (0) = 1, \overset{⌢}{ƒ} (0) = 0, \overset{⌢}{θ} (0) = 1, N_{b} \overset{⌢}{ϕ^{'}} (0) + N_{t} \overset{⌢}{θ^{'}} (0) = 0, \\ f^{'} (\infty) = 0, \overset{⌢}{θ} (\infty) = 0, \overset{⌢}{ϕ} (\infty) = 0 . \end{array}

()

Now

ℜ_{n}^{\overset{⌢}{f}} (ξ) = f_{n - 1}^{‴} - (k_{1} + M) f_{n - 1}^{'} - (1 + F_{1}) {f^{'}}_{n - 1}^{2} + \sum_{j = 0}^{w - 1} {\overset{⌢}{f}}_{w - 1 - j} {\overset{⌢}{f}}_{j}^{″}

()

ℜ_{n}^{\overset{⌢}{θ}} (ξ) = \frac{1}{\Pr} (1 + \frac{3}{4} Rd) {\overset{⌢}{ϕ}}_{n - 1}^{″} + N_{b} \sum_{j = 0}^{w - 1} {\overset{⌢}{ϕ^{'}}}_{w - 1 - j} {\overset{⌢}{θ}}_{j}^{'} + N_{t} {\overset{⌢}{θ^{'}}}_{n - 1}^{2} + Ec (γ {\overset{⌢}{f}}_{n - 1}^{″} + k_{1} {\overset{⌢}{f}}^{'}_{n - 1}^{2}) + \sum_{j = 0}^{w - 1} {\overset{⌢}{θ}}_{w - 1 - j}^{'} {\overset{⌢}{f}}_{j}

()

ℜ_{n}^{\overset{⌢}{ϕ}} (ξ) = {\overset{⌢}{ϕ}}_{n - 1}^{″} - L_{e} \Pr \sum_{j = 0}^{w - 1} {\overset{⌢}{f}}_{w - 1 - j} {\overset{⌢}{ϕ}}_{j}^{'} + \frac{N_{t}}{N_{b}} {\overset{⌢}{θ^{″}}}_{n - 1}

()

Here, χ_{n} = \{\begin{cases} 0, if ζ \leq 1 \\ 1, if ζ > 1 . \end{cases}

()

4 RESULTS AND DISCUSSION

We transform the modeled partial differential equations to ODEs by choosing some suitable transformation for some reasons one is to make the problem solution comfortable and one is to generate some physical parameters in the equation, Due to these generated physical parameters in the ODEs we easily analyze the flow of the fluid in the assumed geometry. In order to overcome such problems one need to use a suitable method. HAM is one of such technique to determine solution for such kind of problems. For this purpose mathematica software is used. In our problem the generated physical parameters are inertial parameter F₁, magnetic field parameter M, Brinkman viscosity number γ, porosity parameter k₁, thermophoresis factor N_t, Brownian number N_b, radiation parameter Rd, Eckert number Ec, and Prandtl number Pr. Now in the preceding section we are moving to deliberate the effect of these said factors on the dimensionless velocity, temperature and concentration distributions of the nanofluid flow. In more we also discuss the effect of the physical factors on the Nusselt number and skin fraction through Table 4_.

4.1 Velocity profile

From Figure 2 we observed that velocity is a falling role of magnetic parameter. As a matter of fact, with increase in the magnetic field, the Lorentz force additionally hops up that demonstrations inverse way to flow of liquid which eventually decreases the movement of the flow. Thus escalating values of the magnetic factor decreases the velocity distribution. Figure 3 depicts the influence of inertial parameter upon velocity distribution. It is observed that incremental jumps in the estimations of F₁ decays velocity distribution. Physically the increase in inertial parameter (i.e., Forchheimer parameter) means there is an increase in pore gap of the medium (or larger pores sizes). This physical phenomenon increases the viscous intervention and ultimately causes a resistance in the flow path. Moreover, there is a negligible impact of F₁ on free stream velocity distribution as displayed in Figure 3. The impact of porosity factor k₁ upon velocity profile can be observed in Figure 4. Along these lines, the thickness of the momentum's limit layer is decreased, and less volume from the nanoliquid is fluxed. The reason behind the physical marvel is the pores of a permeable material that decays the velocities. We see from this figure that there is a reduction in velocity distribution with augmentation of porosity parameter values.

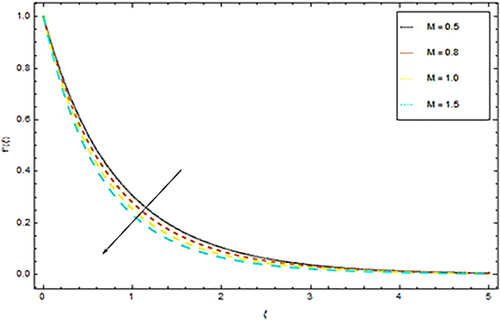
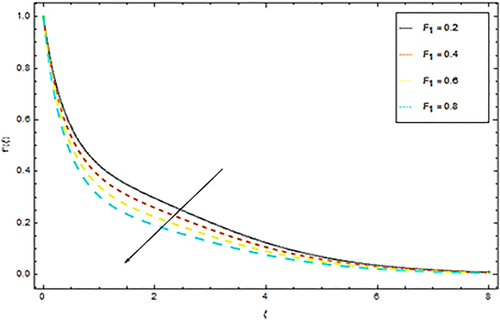
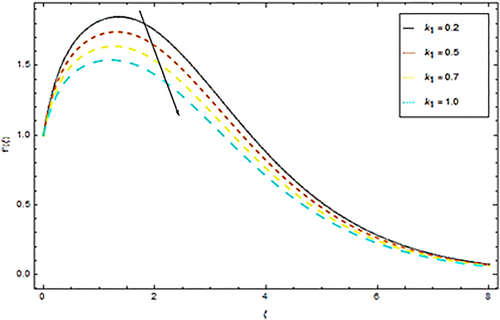
4.2 Temperature profile

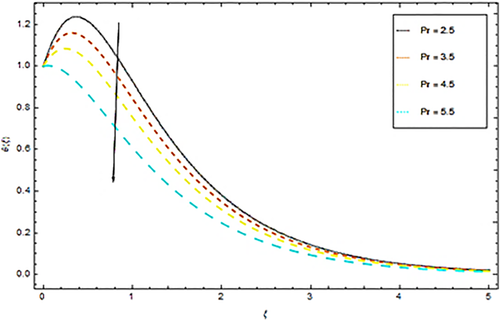
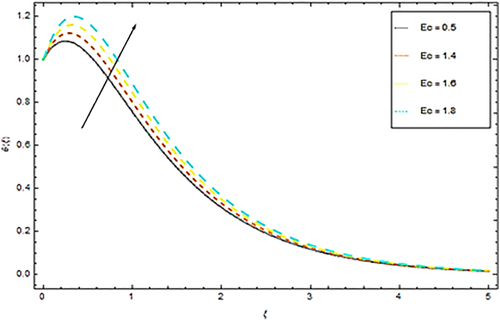
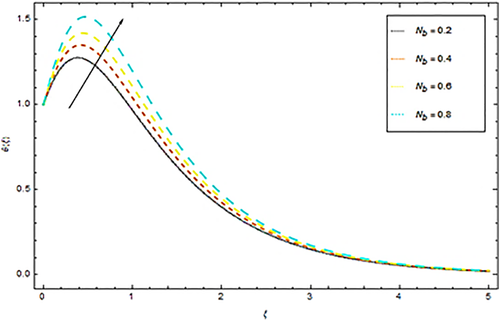
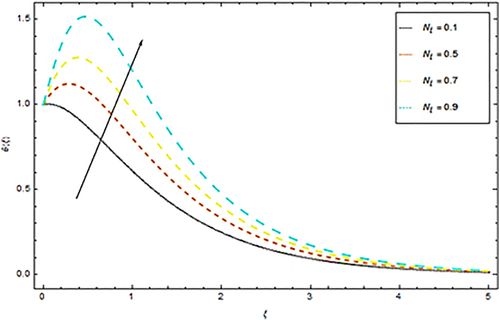
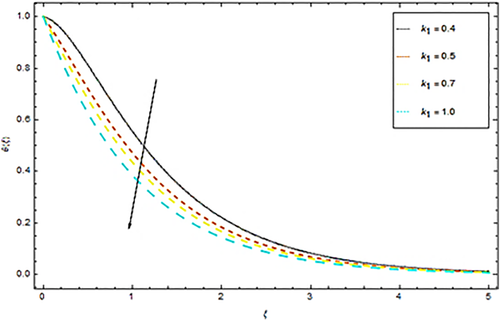
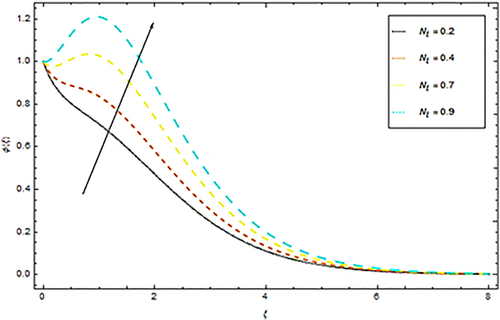
Impact of Prandtl number Pr upon temperature θ(ξ) is discussed in Figure 5. It is obvious from this Figure 5 that an augmentation in Pr reduces the temperature profile θ(ξ) of the fluid. Since an increment in Pr reduces thermal conductivity of nanoparticles that results in the decline of heat transmission rate of stretching surface. This physical phenomenon drops down the thermal boundary layer and hence temperature profile reduces ultimately. Impact of Ec on temperature is shown in Figure 6. From this figure we see that with enhancement of Eckert number Ec the dimensionless temperature θ(ξ) also increases. Actually the augmentations in Ec increase thermal boundary layer which result in alteration of internal kinetic energy into heat energy. In this physical phenomenon temperature of the nanoparticles also increases. Impact of N_b upon dimensionless temperature is given in Figure 7. From this Figure 7 we understand that advancement in N_b prompts casual acceleration in nanoparticles. Physically, the flighty movement of liquid bundles showed up because of an expanding pattern in Brownian movement, along these lines an upgrading nature of temperature profile is noted. Figure 8 presents impact of thermophoretic parameter N_t upon temperature distribution. The spread of liquid units from the hotter to the colder level and builds the warm limit layer for the stream framework. Consequently the expansion in thermophoretic parameter N_t increases temperature of nanofluid. Figure 9 depicts impact of Brinkman viscosity number γ upon temperature. It is obvious from this Figure 9 that θ(ξ) profile is a developing function of Brinkman number. A reduction in temperature within boundary layer is also observed with growing estimations of porosity factor is given in Figure 10. From Figure 11 we see an increasing behavior in temperature profile with augmentation in radiation parameter Rd. Actually an augmentation in Rd results in increasing of thermal boundary layer thickness and hence temperature of nanofluid rises.

4.3 Concentration profile

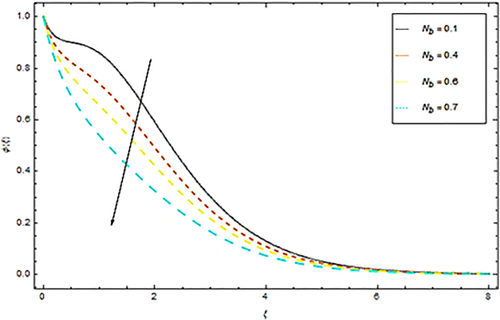
Next we discuss impact of N_b, N_t, and L_e upon concentration distribution. From Figure 12 we see that increasing values of Brownian parameter reduces concentration of nanoparticles. Physically, the Brownian movement is more grounded if there should be an occurrence of more modest nanoparticles which compares to bigger the N_b value and opposite is the circumstance for more modest estimations of N_b. Since for rising estimations of N_b boundary layer thickness with small concentration is produced. Therefore, augmentation in Brownian motion parameter reduces concentration profile. Figure 13 depicts influence of thermophoretic parameter upon concentration. For increasing values of N_t concentration of nanofluid also enhances. The concentration bends for various estimations of Lewis number have been appeared in Figure 14. From the definition of Lewis number, it is clear that an increment in Lewis number might be a direct result of a bigger thermal diffusivity of the liquid for a steady mass diffusivity. This reasons an upsurge of the flow within the boundary layer. Moreover increasing estimations of Lewis number reduces concentration distribution as given in Figure 14.

5 TABLE DISCUSSION

In this subsection, some numerical tables are constructed to discuss the impact of various physical parameters involved in the modeled problem. Tables 1–3 are given below to discuss the effect of these constraints upon velocity, temperature, and concentration distributions respectively for flow problems. Moreover, the effect of various physical parameters upon Nusselt number, skin friction, and Sherwood number is exposed in Tables 4 and 5.

TABLE 1. Impact of various parameters over velocity profiles f(ξ) and f^′(ξ)

F₁	k₁	M	f(ξ)	f^′(ξ)
0.1	0.2	0.6	1.0330098	0.1863375
0.2			1.0448403	0.1893591
0.3			1.0567900	0.1924143
	0.1		1.0125005	0.1799903
	0.2		1.0330098	0.1863374
	0.3		1.0537430	0.1927703
		0.1	0.9326803	0.1554484
		0.2	0.9523051	0.1614577
		0.3	0.9721494	0.1675508

TABLE 2. Effect of different parameters over temperature profile θ(ξ)

Le	M	Pr	Ec	k₁	Rd	θ(ξ)
0.3	0.45	0.35	0.25	0.15	0.52	0.3103688
0.4						0.3103636
0.5						0.3103584
	0.3					0.3103627
	0.4					0.3103668
	0.5					0.3103709
		0.3				0.2982102
		0.4				0.3192600
		0.5				0.3313846
			0.3			0.3105538
			0.4			0.3109237
			0.5			0.3112937
				0.3		0.3100421
				0.4		0.3098233
				0.5		0.3096038
					0.3	0.3188189
					0.4	0.3149996
					0.5	0.3111442

TABLE 3. Effect of different parameters over temperature profile ϕ(ξ)

M	Le	Pr	ϕ(ξ)
0.4	0.2	0.3	0.3515605
0.5			0.3522047
0.6			0.3528510
	0.4		0.4242647
	0.5		0.4598081
	0.6		0.4948172
		0.1	7.3106112
		0.2	1.6149283
		0.3	0.3515605

TABLE 4. Impact of different parameters over Skin fraction and Nusselt Number

M	Pr	Ec	k₁	Rd	γ	F₁	f^′′(0)	−θ^′(0)
0.3	0.35	0.25	0.15	0.52	0.30	0.17	1.3073906	-
0.4							1.3452373	-
0.5							1.3820391	-
0.6							1.4178765	-
	0.1						-	0.2504054
	0.2						-	0.3039555
	0.3						-	0.3595777
	0.4						-	0.4162472
		0.1					-	0.3728367
		0.2					-	0.3828395
		0.3					-	0.3928422
		0.4					-	0.4028448
			0.1				1.2885427	0.3916417
			0.2				1.3268252	0.3841455
			0.3				1.3640348	0.3770494
			0.4				1.4002552	0.3703131
				0.1			-	1.1609536
				0.2			-	0.7249261
				0.3			-	0.5515173
				0.4			-	0.4608888
					0.1		-	0.3683399
					0.2		-	0.3830912
					0.3		-	0.3978435
					0.4		-	0.4125957
						0.1	1.2903560	-
						0.2	1.3152446	-
						0.3	1.3397070	-
						0.4	1.3637635	-

TABLE 5. Impact of different parameters over Sherwood number

N_t	L_e	N_b	−ϕ(ξ)
0.4	1	0.3	0.2705701
0.5			0.4642017
0.6			0.4810516
	1		0.4542206
	2		0.2678081
	3		0.1648102
		0.3	4.4106102
		0.5	2.6159202
		0.7	1.1602704

6 CONCLUSIONS

An investigation of MHD Darcy-Forchheimer flow is carried out in this article. Viscous dissipation and thermal radiation are also measured for flow system over a stretching and porous surface. HAM is utilized to solve transformed modeled equations. Outcome of various parameters upon fluid flow is discussed with the help of graphs. After detail study flowing observation are made.

Increasing values of magnetic parameter increases Lorentz force and hence reduces velocity profile.
Temperature is a developing function of Brinkman number, radiation parameter, and a declining function of porosity parameter.
An augmentation in inertial/Forchheimer parameter causes a reduction in fluid velocity distribution. Moreover velocity is also a reducing function of porosity parameter as it has an adverse effect on velocity profile.
The rise in Brownian motion parameter increases thermal boundary layer and hence temperature of fluid upsurges. Same effects upon temperature profile are also observed for upsurge in thermophoretic factor.
Augmentation in Prandtl number decreases thermal conductivity of nanoparticles that results in the decline of heat transmission rate of stretching surface and hence temperature of fluid drops.
Concentration profile is growing function of thermophoretic parameter and a reducing function of Brownian motion parameter and Lewis number.

ACKNOWLEDGMENTS

The authors acknowledged the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.

CONFLICT OF INTEREST

The authors declare no competing interests.

NOMENCLATURE

V = (u, v): velocity field
(x, y): polar coordinates
σ₁: Stefan Boltzman constant (kg s⁻³ k⁻⁴)
σ₀: magnetic permeability (NA⁻²)
M: magnetic field parameter
Pr: Prandtl number
β₀: applied magnetic field
C_w, C_∞: concentration near and far away the surface respectively
T_w: surface temperature
C_w: surface concentration
w: condition on surface
F₁: inertia coefficient
k₁: porosity parameter
R: radiation parameter
ρ_nf: density (kg m⁻³)
θ: dimensionless temperature (−)
(ρc_p)_nf: nanofluid heat capacity (m²s⁻²K⁻¹)
L_e: Lewis number (−)
μ_nf: dynamic viscosity (kg m⁻¹ s⁻¹)
γ: curvature parameter (−)
χ: mean absorption coefficient (−)
T: temperature of the fluid
γ: curvature parameter (−)
∞: ambient condition
k: thermal conductivity (W m⁻¹ K⁻¹)
Ec: Eckert number
Re_x: Reynolds number
Nu: Nusselt number
C_f: skin friction coefficient
q_r: radiative heat flux (kg s⁻¹)
T_w, T_∞: temperatures near and far away the surface respectively
μ_e: effective viscosity (−)
μ_nf: dynamic viscosity (kg m⁻¹ s⁻¹)
γ: Brinkman viscosity number
C: concentration of the Fluid
ν: kinematic viscosity
ϕ: dimensionless concentration (−)
σ_nf: electrical conductivity
f': dimensionless velocity (−)
': differentiation w.r.t ξ
ξ: similarity variable (−)
Q: heat flux (J s⁻¹)

Biographies

MUHAMMAD JAWAD received the M.Sc and the Ph.D. degree in Applied Mathematics from Abdul Wali Khan University Mardan, Pakistan. He is currently a Lecturer with the Mathematics Department, University of Swabi, Pakistan. His research interests include Entropy optimization, Nanofluid, Darcy -Forchheimer, Computational fluid dynamics, Simulation, Heat transfer, MHD, Bio mathematics and Magnetohydrodynamic.
ANWAR SAEED received the MPhil degree in Mathematics from Islamia College University, Peshawar, Pakistan, and the Ph.D. degree in Applied Mathematics from Abdul Wali Khan University Mardan, Pakistan. He is currently a Principal with the Education Department, Khyber Pakhtunkhwa, Pakistan. His research interests include Nanofluid, Computational fluid dynamics, Simulation, Heat transfer, Nonlinear science, Magnetohydrodynamic, and Bio mathematics.
Dr. Zahir Shah Received MSc Degree from university of Malaknad lower Dir chakdara, KPK,Pakistan and MPhil degree from Islamia college university Peshawar Pakistan. He got PHD degree from abdul wali khan university Mardan Pakistan. He is currently doing Post doc in Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, Science Laboratory Building, King Mongkut's University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, Thrung Khru, Bangkok 10140, Thailand.His research interests are Nanofluid, CFD, simulation, heat transfer, MHD, Hall Effect, Mesoscopic modeling, Nonlinear Science, Magnetohydrodynamic,Ferrohydrodynamic,Electrohydrodynamic and Heat exchangers.
Professor Saeed Islam He received MSc Degree from Quaid-e-Azam University, Islamabad, Pakistan. He got PhD degree from Harbin Institute of Technology Shenzhen Graduate School, CHINA. He is currently working as Professor/Chairman Department of Mathematics, Abdul Wali Khan University, Mardan, KPK, Pakistan. His research interests are Nanofluid, CFD, simulation, heat transfer, MHD, Bio mathematics, Mesoscopic modeling, Nonlinear Science, Magnetohydrodynamic, Ferrohydrodynamic, Electrohydrodynamic and Heat exchangers. He has written several papers and books in various filed of mechanical engineering.
Poom Kumam received his Ph.D. degree in mathematics from Naresuan University, Thailand. He is currently a full Professor at the Department of Mathematics, King Mongkut's University of Technology Thonburi (KMUTT). He is also the Head of KMUTT Fixed Point Theory and Applications Research Group and the Theoretical and Computational Science Center (TaCS-Center) at KMUTT. In addition, He is the Director of Computational and Applied Science for Smart Innovation Cluster (CLASSIC Research Cluster), KMUTT. He has authored or co-authored more than 400 international peer reviewed journals and his main research interests include fixed point theory and applications, computational fixed point algorithms, nonlinear optimization and control theory, optimization algorithms.

REFERENCES

1Muskat M. The Flow of Homogeneous Fluids Through Porous Media. MI: Edwards; 1946.
Web of Science® Google Scholar
2Pal D, Mondal H. Hydromagnetic convective diffusion of species in Darcy-Forchheimer porous medium with non-uniform heat source/sink and variable viscosity. Int Commun Heat Mass Transf. 2012; 39: 913-917.
10.1016/j.icheatmasstransfer.2012.05.012
Web of Science® Google Scholar
3 Ganesh NV, Hakeem AKA, Ganga B. Darcy-Forchheimer flow of hydromagnetic nanofluid over a stretching/ shrinking sheet in a thermally stratified porous medium with second order slip, viscous and Ohmic dissipations effects. Ain Shams Eng J. 2016; 9(4): 939-951. https://doi.org/10.1016/j.asej.2016.04.019.
10.1016/j.asej.2016.04.019
Web of Science® Google Scholar
4Hayat T, Muhammad T, Al-Mezal S, Liao SJ. Darcy-Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int J Numer Methods Heat Fluid Flow. 2016; 26: 2355-2369.
10.1108/HFF-08-2015-0333
Web of Science® Google Scholar
5Muhammad T, Alsaedi A, Shahzad SA, Hayat T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin J Phys. 2017; 55: 963-976.
10.1016/j.cjph.2017.03.006
CAS Web of Science® Google Scholar
6Vaidyanathan G, Sekar R, Hemalatha R, Vasanthakumari R, Senthilnathan S. Soret-driven ferrothermohaline convection. J Magnet Magn Mater. 2005; 288: 460-469.
10.1016/j.jmmm.2004.09.137
CAS Web of Science® Google Scholar
7Kim MC. Linear stability analysis on the onset of Soret driven motion in nanoparticles suspension. Eur Phys J. 2011; 34:27.
CAS Web of Science® Google Scholar
8Hemalatha R, Sekar R, Vaidyanathan G. Effect of dust particles on a Soret-driven ferrothermohaline convection in a rotating medium. Int J Appl Mech Eng. 2012; 17(2): 367-381.
CAS Google Scholar
9Hemalatha R, Sekar R, Vaidyanathan G. Effect of rotaion on a Soret-driven thermohaline convection in a dusty ferrofluids saturating a porous medium. Int J Appl Mech Eng. 2011; 16(4): 1021-1036.
CAS Google Scholar
10Rosensweig RE, Kaiser R, Miskolczy G. Viscosity of magnetic fluid in a magnetic field. J Colloid Interface Sci. 1969; 29(4): 680-686.
10.1016/0021-9797(69)90220-3
CAS Web of Science® Google Scholar
11Shivakumara IS, Nanjundappa CE. Onset of convection in a sparsely packed porous layer with throughflow. Arch Mech. 2001; 53: 219-241.
CAS Google Scholar
12 Jawad M, Shah Z, Islam S, Bonyah E, Khan AZ. Darcy-Forchheimer flow of MHD nanofluid thin film flow with joule dissipation and Navier's partial slip. J Phys Commun 2018; 2: 115014. https://doi.org/10.1088/2399-6528/aaeddf.
10.1088/2399-6528/aaeddf
CAS Web of Science® Google Scholar
13Jawad M, Shah Z, Islam S, et al. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry. 2019; 11: 207. https://doi.org/10.3390/sym11020207.
10.3390/sym11020207
CAS Web of Science® Google Scholar
14 Jawad M, Shah Z, Khan AZ, Khan W, Kumam P, Islam S. Entropy generation and heat transfer analysis in MHD unsteady rotating flow for aqueous suspensions of carbon nanotubes with nonlinear thermal radiation and viscous dissipation effect. Entropy. 2019; 21: 492. https://doi.org/10.3390/e21050492.
10.3390/e21050492
CAS Web of Science® Google Scholar
15Gul T, Haris A, Muhammad AK, Ilyas K, Kumam P. Integer and non-integer order study of the GO-W/GO-EG nanofluids flow by means of Marangoni convection. Symmetry. 2019; 11: 640. https://doi.org/10.3390/sym11050640.
10.3390/sym11050640
CAS Web of Science® Google Scholar
16 Hayat T, Shah F, Hussain Z, Alsaedi A. Darcy Forchheimer flow of Jeffrey nanofluid with heat generation/absorption and melting heat transfer. Therm Sci. 2019; 23: 3833-3842. https://doi.org/10.2298/TSCI171222314H.
10.2298/TSCI171222314H
Web of Science® Google Scholar
17Kausar MS, Hussanan A, Mamat M, Ahmad B. Boundary layer flow through Darcy–Brinkman porous medium in the presence of slip effects and porous dissipation. Symmetry. 2019; 11(5): 659. https://doi.org/10.3390/sym11050659.
10.3390/sym11050659
CAS Web of Science® Google Scholar
18 Madhu M, Gireesha BJ, Kishan N. MHD boundary layer flow and heat transfer to Sisko nanofluid past a nonlinearly stretching sheet with radiation. Int J (AAM). 2018; 9: 28.
Web of Science® Google Scholar
19Gorla RSR, Chamkha A. Natural convective boundary layer flow over a vertical plate embedded in a porous medium saturated with a non-Newtonian nanofluid. Int J Microscale Nanoscale Therm Fluid Transp Phenom. 2011; 3: 1-20.
Google Scholar
20Dogonchi AS, Chamkha AJ, Seyyedi SM, Ganji DD. Radiativenanofluid flow and heat transfer between parallel disks with penetrable and stretchable walls considering Cattaneo–Christov heat flux model. Heat Transf Asian Res. 2018; 47: 735-753.
10.1002/htj.21339
Web of Science® Google Scholar
21Goshayeshi HR, RSafaei M, Goodarzi M, Dahari M. Particle size and Type E_ects on heat transfer enhancement of ferro-nanofluids in a pulsating heat pipe under magnetic field. Powder Technol. 2016; 301: 1218-1226.
10.1016/j.powtec.2016.08.007
CAS Web of Science® Google Scholar
22Khanafer K, Vafai K. A critical synthesis of thermophysical characteristics of nanofluids. Int J Heat Mass Transf. 2012; 54: 4410-4428.
10.1016/j.ijheatmasstransfer.2011.04.048
Web of Science® Google Scholar
23 Mital M. Analytical analysis of heat transfer and pumping power of laminar nanofluid developing flow in microchannels. Appl Therm Eng. 2013; 50: 429-436.
10.1016/j.applthermaleng.2012.07.040
CAS Web of Science® Google Scholar
24Hung TC, Yan WM, Wang XD, Chang CY. Heat transfer enhancement in microchannel heat sinks using nanofluids. Int J Heat Mass Transf. 2012; 55: 2559-2570.
10.1016/j.ijheatmasstransfer.2012.01.004
CAS Web of Science® Google Scholar
25Akbari OA, Toghraie D, Karimipour A. Impact of ribs on flow parameters and laminar heat transfer of water–aluminum oxide nanofluid with different nanoparticle volume fractions in a three-dimensional rectangular microchannel. Adv Mech Eng. 2015; 7: 1-11.
10.1177/1687814015618155
CAS Web of Science® Google Scholar
26Behnampour A, Akbari OA, Safaei MR, et al. Analysis of heat transfer and nanofluid fluid flow in microchannels with trapezoidal, rectangular and triangular shaped ribs. Phys E. 2017; 91: 15-31.
10.1016/j.physe.2017.04.006
CAS Google Scholar
27Gravndyan Q, Akbari OA, Toghraie D, et al. The effect of aspect ratios of rib on the heat transfer and laminar water/TiO2 nanofluid flow in a two-dimensional rectangular microchannel. J Mol Liq. 2017; 236: 254-265.
10.1016/j.molliq.2017.04.030
CAS Web of Science® Google Scholar
28Alfven H. Existence of electromagnetic-hydrodynamic waves. Nature. 1942; 150: 405-406.
10.1038/150405d0
Google Scholar
29Ishak A, Nazar R, Pop I. Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers Manag. 2008; 49(11): 3265-3269.
10.1016/j.enconman.2007.11.013
Web of Science® Google Scholar
30 Hayat T, Riaz R, Arsalan A. Analysis of entropy generation for MHD flow of third grade nanofluid over a nonlinear stretching surface embedded in a porous medium. Phys Scr. 2019; 94: 125703.
10.1088/1402-4896/ab3308
CAS Web of Science® Google Scholar
31Farooq U, Dianchen L, Munir S, Ramzan M, Suleman M, Hussain S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci Rep. 2019; 9:7312.
10.1038/s41598-019-43549-0
PubMed Web of Science® Google Scholar
32 Kumar SG et al. Three-dimensional conducting flow of radiative and chemically reactive Jeffrey fluid through porous medium over a stretching sheet with Soret and heat source/sink effects. Results Eng. 2020: 2020. https://doi.org/10.1016/j.rineng.2020.100139.
Google Scholar
33Lahmar S, Kezzar M, Eid MR, Sari MR. Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Phys A Stat Mech Appl. 2020; 540:123138.
10.1016/j.physa.2019.123138
CAS Web of Science® Google Scholar
34Durgaprasad P, Varma S, Hoque MM, Raju C. Combined effects of Brownian motion and thermophoresis parameters on three-dimensional (3D) Casson nanofluid flow across the porous layers slendering sheet in a suspension of graphene nanoparticles. Neural Comput Appl. 2019; 31: 6275-6286.
10.1007/s00521-018-3451-z
Web of Science® Google Scholar
35Ganga B, Ansari SMY, Ganesh NV, Hakeem AA. MHD flow of Boungiorno model nanofluid over a vertical plate with internal heat generation/absorption. Prop Power Res. 2016; 5: 211-222.
Web of Science® Google Scholar

All articles

An optimal analysis for magnetohydrodynamics Darcy-Forchheimer boundary layer radiative flow past a porous medium

Abstract

1 INTRODUCTION

2 MATHEMATICAL FORMULATION

3 SOLUTION METHOD