An explanation of the Bernstein-Vazirani and Deustch-Josza algorithms with the quantum stabilizer formalism

2.1 Computational quantum states

In this article, ${({ℂ}^2)}^{\otimes n}\cong {ℂ}^{2^n}$ will be a 2ⁿ−dimensional Hilbert space of n ≥ 1 qubits, with a computational basis $B=\{|i⟩:i\in {𝔽}_2^n\}$ (here ${𝔽}_2$ denotes the Galois field of two elements $\mathbb{Z}/2\mathbb{Z}=\{0,1\}$¹¹). Elements in ${({ℂ}^2)}^{\otimes n}$, written |x⟩, are given by the $ℂ$-linear combinations of the elements in B, that is, $|x⟩={\sum }_{i\in {𝔽}_2^n}{\lambda }_i|i⟩$. The coefficients ${\lambda }_i$ are called “amplitudes,” and the element is assumed to be normalized, that is, of complex norm equal to one: $\Vert x\Vert =\sqrt{⟨x|x⟩}$ (here ⟨x| denotes the transpose conjugate of the element x, that is, $⟨x|={\left({\sum }_{i\in {𝔽}_2^n}\overline{{\lambda }_i}|i⟩\right)}^T$). Normalized quantum states are the states used in quantum computation.

2.2 Evolution of the quantum states

A complex 2ⁿ × 2ⁿ−invertible matrix $U={(U_{kl})}_{1\le k,l\le n}\in GL(2^n,ℂ)$ will be called “unitary” if $U·U^{†}=U^{†}·U=I_{2^n}$, where $U^{†}={(\overline{U_{lk}})}_{1\le k,l\le n}$ denotes its conjugate transposed matrix. These matrices represent the set of possible transformations that can be driven by a quantum computation, which has a group structure under multiplication, denoted U(2ⁿ) and called “unitary group.” Another important class of matrices is given by the Hermitian ones, that is, those H ∈ U(2ⁿ) such that H = H^†. The set of Hermitian matrices is a $\frac{2^n(2^n+1)}{2}-$dimensional complex vector space, which is related to the unitary group via the Schrödinger equation $H(t)|x(t)⟩=i\hslash \frac{d}{dt}|x(t)⟩$, where H(t) denotes the Hamiltonian driving the time-dependent quantum state |x(t)⟩, i is the complex unity, and $\hslash$ is Planck reduced constant (see 2.2.2 of Reference 5). Such a Hamiltonian is given by a Hermitian matrix, and the solution to such an equation is U(t) |x(0)⟩, where $U(t)=e^{-i\frac{H(t)}{\hslash }}$ is a unitary matrix.

2.3 Measurements

Measures of a quantum state |x⟩ are given by a set of “measurement operators” ${\{M_m\}}_{m\in \mu }\subseteq {ℳ}_{2^n}(ℂ)$, where $\mu \in \mathbb{N}$, satisfying the “completeness equation” $I_{2^n}={\sum }_{m\in \mu }{M}_m^{†}{M}_m$. The output of such a measure on |x⟩ is probabilistically the vector M_m|x⟩, suitably normalized by the square of p(m) = ⟨x|M_m|x⟩ (ie, ⟨x|M_m · x⟩). The number p(m) represents the actual probability of such a measure. Usually, measures are carried over the computational state basis, and so the measurement operators are ${\{|i⟩⟨i|\}}_{i\in {𝔽}_2^n}$. In this case, the probability of obtaining |i⟩ after measurement of the quantum state ${\sum }_{i\in {𝔽}_2^n}{\lambda }_i|i⟩$ is $|{\lambda }_i{|}^2=\overline{{\lambda }_i}·{\lambda }_i$.

2.4 The Pauli group

2.5 Centralizer of subgroups of the Pauli group

From here, it follows that if S is a nonempty subset of G_n, then its centralizer $C_{G_n}(S)$ is equal to {U ∈ G_n | w(U) ⊥ w(T), for all T ∈ S}. It will be denoted by S^⊥. In particular, the center of G_n is $Z(G_n)=\{i^k{I}_{2^n}|0\le k\le 3\}$, a cyclic group of order 4, and $w:G_n/Z(G_n)\to {𝔽}_2^{2n}$ is a well-defined group isomorphism (from a multiplicative group to an additive group). The “quantum weight” of an element U ∈ G_n, is defined as the number of 1 ≤ i ≤ n such that a_i ≠ 0 or b_i ≠ 0, where w(U) = (a|b).

2.6 The main theorem of the stabilizer formalism

The following result is the fundamental basis of the stabilizer formalism.

This theorem states that, up to a global phase, there is a correspondence between certain quantum states of ${({ℂ}^2)}^{\otimes n}$ and elementary abelian 2-subgroups of G_n of dimension n. Moreover, any quantum computation carried out by operators of the Clifford group on one of those states is directly translated into a conjugation operation in the Pauli group. So, certain quantum algorithms that involve circuits containing quantum gates from the Clifford group can be classically simulated (efficiently) by tracking conjugates of n elements of the Clifford group. This fact, along with the corresponding efficiency in the measures described in 10.5.3 of Reference 5, is known as the “Gottesman-Knil theorem.”¹³

Example

Let us illustrate the stabilizer paradigm with the circuit of Figure 1.

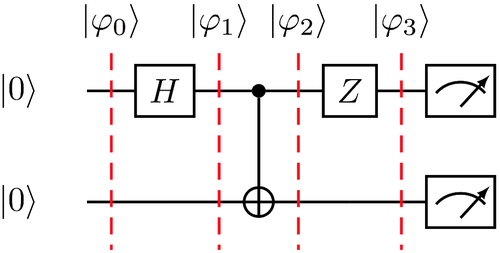
The initial state is |φ₀⟩ = |0⟩ ⊗ |0⟩, with stabilizer subgroup S₀ generated by Z₁ = I ⊗ Z, and Z₂ = Z ⊗ I. Application of the Hadamard gate in the first qubit transforms |φ₀⟩ into $|{\phi }_1⟩=\frac{|0⟩+|1⟩}{\sqrt{2}}\otimes |0⟩$. The corresponding subgroup is obtained by conjugation of ⟨Z₁,Z₂⟩ by the element H ⊗ I, that is, it is S₁ = ⟨X₁ = X ⊗ I,Z₂⟩. The control NOT gate yields the (Bell) state $|{\phi }_2⟩=\frac{|0⟩\otimes |0⟩+|1⟩\otimes |1⟩}{\sqrt{2}}$, and the corresponding stabilizer subgroup S₂ = ⟨X₁ ⊗ X₂,Z₁ ⊗ Z₂⟩. Right before the measurement, we have the quantum state $|{\phi }_3⟩=\frac{|0⟩\otimes |0⟩-|1⟩\otimes |1⟩}{\sqrt{2}}$ (another Bell state), whose stabilizer group is S₃ = ⟨− X₁ ⊗ X₂,Z₁ ⊗ Z₂⟩. Table 1 contains a summary of the quantum states and the stabilizer subgroups corresponding to the circuit of Figure 1.

This formalism explains straighforwardly the familiy of quantum error correcting codes known as “stabilizer codes” (see 10.5.5 of Reference 5). In this context, certain 2^k-dimensional quantum error correcting codes V_S are described by the corresponding elementary abelian 2-subgroups S of G_n of dimension n − k, known as “error group.” The errors with no effect on the quantum state are those effected by elements of S, where as the undetectable errors are those in S^⊥ ∖ S, since they transform the quantum state in another one belonging to the code. The correctable errors are subsets E of G_n such that whenever T,U ∈ E, then T⁻¹U ∉ S^⊥ ∖ S. This set is usually taken as those elements of the Pauli group of quantum weight not greater than $\lceil \frac{d-1}{2}\rceil$, where d is minimum quantum weight of the elements in S^⊥ ∖ S.¹²

3.1 BV

The goal of the BV algorithm is to determine a linear function $f:{𝔽}_2^n\to {𝔽}_2$ from its evaluations. That is, a certain function f is given under the promise that f(x) = x · s, for some binary unknown array $s\in {𝔽}_2^n$ (here again · denotes the standard inner product in ${𝔽}_2^n$). Clasically, this problem requires O(n) evaluations of f (that yield the solution of the corresponding linear system of equations). However, BZ only uses a single (quantum query) evaluation of f. The algorithm, whose quantum circuit can be found in Figure 2, is as follows.

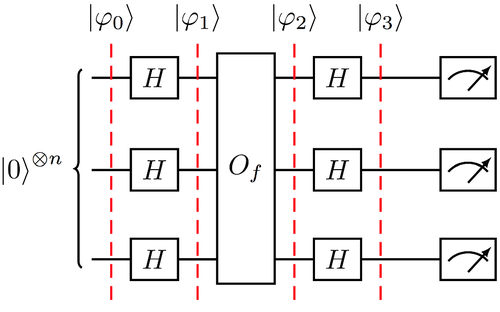
It can be proved that, with probability one, the final measurent gives the quantum state |s⟩, for the desired unknown value s. Let us prove this fact under the stabilizer formalism, in a straightforward way.

Since |0⟩ is an eigenvector of the Pauli matrix Z (with eigenvalue 1), it is clear that the initial sate |0^⊗n⟩ is stabilized by any matrix of the form Z(e_i), where $e_i=(0\dots 0\stackrel{(i}{1}0\dots 0)$ is an element in the standard basis of ${𝔽}_2^n$. The subgroup S of G_n generated by those n matrices is abelian, since the elements ${\{e_i\}}_{i=1}^n$ are pairwise orthogonal, with respect to the bilinear form ⋆ (ie, ${𝔽}_2^n\times \{0\}$ is a totally isotropic subspace of $({𝔽}_2^{2n},\star )$).

Since HZH^† = X, we have that application of the Walsh-Hadamard transform H^⊗n on the initial state is equivalent to applying the conjugation by H^⊗n on each of the matrices Z(e_i), and so the stabilizer subgroup is generated by the n matrices ${\{X(e_i)\}}_{i=1}^n$.

Now, it follows the application of the phase oracle O_f. Observe that, for all 1 ≤ i ≤ n, and $s_i\in {𝔽}_2$, the operator $Z_i^{s_i}$ transforms the quantum state |x⟩ of the computational basis, into ${(-1)}^{s_i·x_i}|x⟩$ (when x_i = 0, the state remains the same, and it takes an opposite global phase when x_i = 1). Therefore, because of linearity $O_f|x⟩={(-1)}^{f(x)}|x⟩={(-1)}^{x·s}|x⟩={(-1)}^{x_1·s_1}·\dots ·{(-1)}^{x_n·s_n}|x⟩=Z(s)|x⟩$, for all $|x⟩\in {ℂ}^{\otimes n}$. Hence, the action of the phase oracle on the quantum state is translated into conjugation by the element Z(s), that is, since ZXZ^† = −X, those 1 ≤ i ≤ n with s_i = 0 have an unmodified X(e_i) as generator of the stabilizer subgroup, whereas those with s_i = 1 provide by conjugation the generator −X(e_i). Summarizing, the stabilizer subgroup is generated by ${\{{(-1)}^{s_i}X(e_i)\}}_{i=1}^n$. Incidentally, notice that the oracle O_f, is an element of the Pauli group (and so in particular of the Clifford group), so the algorithm can be efficiently realised via the Gottesman-Knill theorem.

A second application of the operator H^⊗n, because of the relation HXH^† = Z, yields that the stabilizer subgroup finally achieved is generated by the n matrices ${\{{(-1)}^{s_i}Z(e_i)\}}_{i=1}^n$.

Since the Z matrix stabilizes the qubit |0⟩, and −Z stabilizes the qubit |1⟩, we have that, for all 1 ≤ i ≤ n, and $a\in {𝔽}_2$, the matrix (− 1)^aZ stabilizes the quantum state |a⟩. Therefore, the state stabilized by the last subgroup is exactly |s⟩, and so the final measure of the algorithm gives |s⟩ with probability one. A summary of the quantum states and the stabilizer subgroups corresponding to BV algorithm can be found in Table 2.

3.2 DJ

The goal of the DJ algorithm is to determine if a function $f:{𝔽}_2^n\to {𝔽}_2$ is constant or balanced. That is, a certain function f is given under the promise that it is constant (ie, f = 0 or f = 1) or balanced (ie, $M=\#\{x\in {𝔽}_2^n|f(x)=1\}=2^{n-1}$. Clasically, this problem requires O(2^n − 1) evaluations of f (half plus one evaluations are needed in the worst case to distinguish a constant or balanced function). However, DJ only uses a single (quantum query) evaluation of f. The algorithm, whose quantum circuit can be found in Figure 3, is as follows. Observe that, except for the decision taken after the final measurement, the steps of the BV and DJ algorithms are the same. This explains why Figures 2 and 3 are the same.

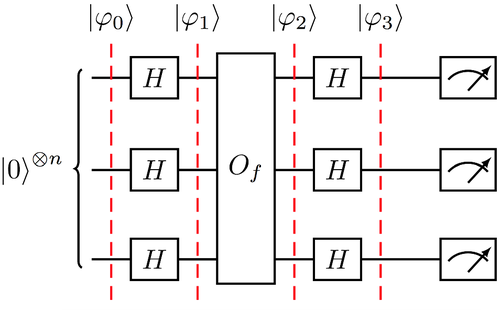
It can be proved that, with probability one, the final measurement gives the quantum state |0^⊗n⟩ if and only if f is constant. When f is balanced, it gives other element of the computational basis. The first two steps in DJ are those of BV, and so the stabilizer subgroup is generated by the n matrices ${\{X(e_i)\}}_{i=1}^n$ after them.

Observe that the quantum circuit of DJ is just like that of BV.

Hence, O_f can be expressed as a nontrivial complex linear combination of the elements in the set $\{Z(b)|b\in {𝔽}_2^n\setminus \{0^n\}\}$. Remember, from the analysis of BV, that the elements in this set correspond to phase oracles of nonzero linear functions. However, unlike BV, this oracle might not correspond to an element of the Clifford group (and as a consequence the algorithm might not be efficiently realisable via the Gottesman-Knill theorem). A measurement of the realizability of the algorithm is the “stabilizer rank,”¹⁴ which in this case is upper bounded by the number of nonzero coefficients of O_f as a linear combination of the elements in the set $\{Z(b)|b\in {𝔽}_2^n\setminus \{0^n\}\}$.

Coming back to the stabilizer formalism analysis of DJ, we have that $O_f=\pm I_{n^2}$, when f is constant, and that $O_f={\sum }_{b\in {𝔽}_2^n}{\lambda }_{b}Z(b)$, for certain complex numbers ${\lambda }_b=⟨O_f|Z(b)⟩$ (with ${\lambda }_{0^n}=0$), when f is balanced. Hence, the action of the phase oracle on the third step of DJ, is translated into conjugation by either $\pm I_{n^2}$, or by a nontrivial linear combination of operators Z(b), with b ≠ 0. In the first case, the stabilizer group after this step is again the one generated by ${\{X(e_i)\}}_{i=1}^n$. In the second case, since $Z(b)X(e_i)Z{(b^{\prime })}^{†}={(-1)}^{b_i}X(e_i)Z(b\oplus b^{\prime })$, the stabilizer subgroup is $O_f⟨X(e_1),\dots ,X(e_n)⟩O_f^{†}={⟨X(e_i)\left({\sum }_{b,b^{\prime }\in {𝔽}_2^n}{\lambda }_b\overline{{\lambda }_{b^{\prime }}}{(-1)}^{b_i}Z(b\oplus b^{\prime })\right)⟩}_{i=1}^n$ (where ⊕ denotes addition in ${𝔽}_2^n$).

Finally, since ${\lambda }_0=0$, the measurement yields with probability one |0^⊗n⟩ if and only if f is constant. A summary of the quantum states and the stabilizer subgroups corresponding to DJ algorithm, can be found in Table 3.