Volume 2, Issue 5 e1114

RESEARCH ARTICLE

Full Access

On the design and analysis of high-order Weerakoon-Fernando methods based on weight functions

Prem B. Chand,

Prem B. Chand

Department of Mathematics, South Asian University, Chanakya Puri, India

Search for more papers by this author

Francisco I. Chicharro,

Corresponding Author

Francisco I. Chicharro

[email protected]

orcid.org/0000-0001-9116-2870

Escuela Superior de Ingeniería y Tecnología, Universidad Internacional de La Rioja, Logroño, Spain

Correspondence Francisco I. Chicharro, Escuela Superior de Ingeniería y Tecnología, Universidad Internacional de La Rioja, Avenida de La Paz 137, Logroño 26006, Spain.

Email: [email protected]

Search for more papers by this author

Pankaj Jain,

Pankaj Jain

Department of Mathematics, South Asian University, Chanakya Puri, India

Search for more papers by this author

Prem B. Chand,

Prem B. Chand

Department of Mathematics, South Asian University, Chanakya Puri, India

Search for more papers by this author

Francisco I. Chicharro,

Corresponding Author

Francisco I. Chicharro

[email protected]

orcid.org/0000-0001-9116-2870

Escuela Superior de Ingeniería y Tecnología, Universidad Internacional de La Rioja, Logroño, Spain

Correspondence Francisco I. Chicharro, Escuela Superior de Ingeniería y Tecnología, Universidad Internacional de La Rioja, Avenida de La Paz 137, Logroño 26006, Spain.

Email: [email protected]

Search for more papers by this author

Pankaj Jain,

Pankaj Jain

Department of Mathematics, South Asian University, Chanakya Puri, India

Search for more papers by this author

First published: 18 June 2020

https://doi.org/10.1002/cmm4.1114

Citations: 1

Funding information: MCIU/AEI/FEDER/UE, PGC2018-095896-B-C22

Share a link

Email
Wechat
Bluesky

Abstract

In this article, using the idea of weight functions on Weerakoon-Fernando's method, an optimal fourth-order method and some higher order multipoint methods for solving nonlinear equations are proposed. These methods are tested in some real applications and numerical examples and the results are compared with some existing methods. Their dynamical behavior on complex polynomials is analyzed and basins of attraction of these methods are presented.

1 INTRODUCTION

Nonlinear equations arise in almost all branches of Science and Engineering. The solution of such equations is rarely obtained by analytical methods, so iterative methods are employed. The most commonly used iterative method to solve the nonlinear equation f(x) = 0 is Newton's method given by

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})},

(1)

which is known to be quadratically convergent for simple zeros. Many mathematicians continue to contribute to Newton's method of improving the order of convergence in several ways.

Weerakoon and Fernando¹ suggests an improvement in the iteration of Newton's method at the expense of an additional first derivative evaluation. The convergent cubic method of Weerakoon and Fernando method is given by

x_{n + 1} = x_{n} - \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (x_{n + 1}^{*})},

(2)

where

x_{n + 1}^{*} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})}

is the Newton's component.

There are various techniques (see References 2-5) for developing new methods and improving the convergence of any iterative method. One of the most effective techniques is the use weight functions. This technique can be applied both on solving nonlinear equations^6-9 and systems of nonlinear equations.^10-12

In Reference 7, authors proposed the following method:

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ x_{n + 1} & = x_{n} - \frac{f (x_{n})}{f^{'} (y_{n})} \cdot H (t_{n}), \end{align}

(3)

where

t_{n} = \frac{f^{'} (y_{n})}{f^{'} (x_{n})}

and H is a weight function. Method (3) was shown to be of order 4 if H(1) = 1,

H^{'} (1) = \frac{1}{4}

H^{″} (1) = \frac{3}{4}

, and |H⁽³⁾(1)| < ∞.

In Reference 9, authors proposed the following fourth-order iterative method using the weight function in Newton's method,

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ x_{n + 1} & = x_{n} - (- \frac{1}{2} + \frac{9}{8} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{3}{8} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \frac{f (x_{n})}{f^{'} (x_{n})} . \end{align}

(4)

In this document, we propose new methods of order 4, 5, 6, and 8 using weight functions and based on the Weerakoon and Fernando method (2). An important ingredient of this article is the dynamical behavior of the introduced methods. It is well known that the dynamical properties of the rational operator give important information about the convergence, efficiency, and stability of the iterative methods. In the last decades, the study of the dynamical behavior of the rational operator associated to an iterative method has become a fast growing area of research (see References 13-17). Furthermore, there is an extensive literature^18-21 on the dynamics of rational functions. We discuss the dynamics of the proposed methods.

The article is organized as follows: Section 2 presents the development of the methods and their corresponding error equations. In Section 3, these methods are tested in some Engineering applications and the results are compared with other known methods. Section 4 covers the dynamics of the methods for analyzing their stability. Finally, Section 5 presents the main conclusions.

2 DEVELOPMENT OF METHODS AND THEIR CONVERGENCES

This section is focused on the generation of iterative methods based on (2) A fourth-order method is generated using a weight function in the second step of (2).

Then a third step is introduced from which different iterative schemes are obtained. On the one hand, we apply a structure similar to (2) and introduce only a new functional evaluation, which results in a method of order five. On the other hand, we use a Newton-type expression with a frozen derivative and a weight function, obtaining two order six methods. Finally, if we directly include Newton's method as a third step we obtain an eighth-order method.

2.1 Fourth-order method

We begin with the two step weighted Weerakoon-type method

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ x_{n + 1} & = x_{n} - (a_{1} + a_{2} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + a_{3} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})} . \end{align}

(5)

Below we prove the convergence of method (5).

Theorem 1.Let f be a complex valued function defined on some interval I having sufficient number of smooth derivatives. Let $α$ be a simple root of the equation f(x) = 0. Then method (5) is of order four if $a_{1} = - \frac{1}{4}$ , $a_{2} = \frac{3}{4}$ , and $a_{3} = \frac{1}{2}$ .

Proof.Let e_n be the error in x_n. Denote $c_{j} = \frac{f^{(j)} (α)}{j! f^{'} (α)}$ . Then in view of Taylor's series expansion, we have

f (x_{n}) = f^{'} (α) (e_{n} + c_{2} e_{n}^{2} + c_{3} e_{n}^{3} + c_{4} e_{n}^{4} + O (e_{n}^{5})) .

(6)

and

f^{'} (x_{n}) = f^{'} (α) (1 + 2 c_{2} e_{n} + 3 c_{3} e_{n}^{2} + 4 c_{4} e_{n}^{3}) + O (e_{n}^{4}) .

(7)

so that,

y_{n} = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})} = α + \frac{e_{n}}{3} + \frac{2}{3} c_{2} e_{n}^{2} - \frac{4}{3} (c_{2}^{2} - c_{3}) e_{n}^{3} + \frac{2}{3} (4 c_{2}^{3} - 7 c_{2} c_{3} + 3 c_{4}) e_{n}^{4} + O (e_{n}^{5}) .

(8)

Now, using Taylor's series expansion of

f^{'} (y_{n})

about

α

, (8) gives

\begin{align} f^{'} (y_{n}) & = f^{'} (α) (1 + \frac{2}{3} c_{2} e_{n} + \frac{1}{3} (4 c_{2}^{2} + c_{3}) e_{n}^{2} - \frac{4}{27} (- 18 c_{2}^{3} + 27 c_{2} c_{3} + c_{4}) e_{n}^{3} \\ + \frac{4}{9} (12 c_{2}^{4} - 24 c_{2}^{2} c_{3} + 6 c_{3}^{2} + 11 c_{2} c_{4}) e_{n}^{4} + O (e_{n}^{5})) . \end{align}

(9)

Now, from (6), (7) to (9), we get

\frac{f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})} = \frac{1}{2} e_{n} - \frac{1}{6} c_{2} e_{n}^{2} - \frac{1}{9} (c_{2}^{2} + 3 c_{3}) e_{n}^{3} + \frac{1}{54} (50 c_{2}^{3} - 15 c_{2} c_{3} - 29 c_{4}) e_{n}^{4} + O (e_{n}^{5}) .

(10)

\begin{align} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} & = 1 + \frac{4}{3} e_{n} - \frac{4}{9} (5 c_{2}^{2} - 6 c_{3}) e_{n}^{2} + \frac{8}{27} (8 c_{2}^{3} - 21 c_{2} c_{3} + 13 c_{4}) e_{n}^{3} \\ - \frac{1}{81} (32 c_{2}^{4} - 540 c_{2}^{2} c_{3} + 288 c_{3}^{2} + 620 c_{2} c_{4} - 405 c_{5}) e_{n}^{4} + O (e_{n}^{5}) . \end{align}

(11)

and

\begin{align} \frac{f^{'} (y_{n})}{f^{'} (x_{n})} & = 1 - \frac{4}{3} e_{n} + \frac{4}{3} (3 c_{2}^{2} - 2 c_{3}) e_{n}^{2} - \frac{8}{27} (36 c_{2}^{3} - 45 c_{2} c_{3} + 13 c_{4}) e_{n}^{3} \\ + \frac{1}{27} (720 c_{2}^{4} - 1332 c_{2}^{2} c_{3} + 288 c_{3}^{2} + 484 c_{2} c_{4} - 135 c_{5}) e_{n}^{4} + O (e_{n}^{5}) . \end{align}

(12)

Using the results (10), (11), and (12) in (5), we obtain the error equation as:

\begin{align} e_{n + 1} & = (1 - a_{1} - a_{2} - a_{3}) e_{n} + \frac{1}{3} (a_{1} - 3 a_{2} + 5 a_{3}) c_{2} e_{n}^{2} \\ + \frac{2}{9} (13 a_{2} c_{2}^{2} - 19 a_{3} c_{2}^{2} - 9 a_{2} c_{3} + 15 a_{3} c_{3} + a_{1} (c_{2}^{2} + 3 c_{3})) e_{n}^{3} \\ + \frac{1}{27} (- 3 a_{2} (42 c_{2}^{3} - 77 c_{2} c_{3} + 25 c_{4}) + a_{1} (- 50 c_{2}^{3} + 15 c_{2} c_{3} + 29 c_{4}) \\ + a_{3} (266 c_{2}^{3} - 393 c_{2} c_{3} + 133 c_{4})) e_{n}^{4} + O (e_{n}^{5}) . \end{align}

In order to cancel the terms of order less than four, we solve the system

\begin{array}{ll} 1 - a_{1} - a_{2} - a_{3} & = 0, \\ a_{1} - 3 a_{2} + 5 a_{3} & = 0, \\ 13 a_{2} c_{2}^{2} - 19 a_{3} c_{2}^{2} - 9 a_{2} c_{3} + 15 a_{3} c_{3} + a_{1} (c_{2}^{2} + 3 c_{3}) & = 0, \end{array}\}

which gives,

a_{1} = - \frac{1}{4}

a_{2} = \frac{3}{4}

, and

a_{3} = \frac{1}{2}

. Consequently, the error equation becomes

e_{n + 1} = \frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + O (e_{n}^{5}) .

and the assertion is proved.

2.2 Fifth-order method

In view of Theorem 1, we obtain the following fourth-order method:

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ x_{n + 1} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})} . \end{align}

(13)

We modify method (13) to increase the order of convergence including a third step. In this regard, we propose the following method:

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{2 f (z_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})} . \end{align}

(14)

Below we prove the convergence of method (14).

Theorem 2.Let f be a complex valued function defined on some interval I having sufficient number of smooth derivatives. Let $α$ be a simple root of the equation f(x) = 0. Then method (14) has fifth-order of convergence.

Proof.Following the proof of Theorem 1 and using terms with more powers of e_n, we obtain

z_{n} = α + \frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + \frac{1}{36} (- 336 c_{2}^{4} + 480 c_{2}^{2} c_{3} - 80 c_{2} c_{4} + 9 (- 8 c_{3}^{2} + c_{5})) e_{n}^{5} + O (e_{n}^{6}) .

(15)

Now, expanding f(z_n) about

α

we get

\begin{align} f (z_{n}) & = f^{'} (α) (\frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} \\ + \frac{1}{36} (- 336 c_{2}^{4} + 480 c_{2}^{2} c_{3} - 80 c_{2} c_{4} + 9 (- 8 c_{3}^{2} + c_{5})) e_{n}^{5} + O (e_{n}^{6})) . \end{align}

(16)

and consequently, we have

\begin{align} \frac{f (z_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})} & = \frac{1}{18} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} \\ + \frac{1}{216} (- 1280 c_{2}^{4} + 1584 c_{2}^{2} c_{3} - 256 c_{2} c_{4} - 216 c_{3}^{2} + 27 c_{5}) e_{n}^{5} + O (e_{n}^{6}) . \end{align}

(17)

Using (15) and (17) in (14), we obtain the error equation as

e_{n + 1} = \frac{4}{27} c_{2} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{5} + O (e_{n}^{6}),

which shows that method (14) has order of convergence five.

2.3 Sixth-order method

Applying some weight functions on the variant of method (14) of order five, higher order methods can be obtained. For instance, we propose the following methods:

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{f (z_{n})}{f^{'} (x_{n})} \cdot (a_{1} + a_{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) . \end{align}

(18)

and

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{f (z_{n})}{f^{'} (y_{n})} \cdot (b_{1} + b_{2} \frac{f^{'} (x_{n})}{f^{'} (y_{n})}) . \end{align}

(19)

Below, we present the theorem of the convergence of methods (18) and (19).

Theorem 3.Let f be a real or complex valued function defined on some interval I having sufficient number of smooth derivatives. Let $α$ be a simple root of the equation f(x) = 0. Then, method (18) is of order six, if $a_{1} = \frac{5}{2}$ and $a_{2} = - \frac{3}{2}$ . In addition, method (19) is of order six, if $b_{1} = b_{2} = \frac{1}{2}$ .

Proof.It is easy to calculate from (7), (9) to (16), that

\frac{f (z_{n})}{f^{'} (x_{n})} = \frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + \frac{1}{36} (- 472 c_{2}^{4} + 552 c_{2}^{2} c_{3} - 88 c_{2} c_{4} + 9 (- 8 c_{3}^{2} + c_{5})) e_{n}^{5} + O (e_{n}^{6}),

(20)

and

\frac{f (z_{n})}{f^{'} (y_{n})} = \frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + (\frac{- 286}{27} c_{2}^{4} + 14 c_{2}^{2} c_{3} - 2 c_{3}^{2} - \frac{62}{27} c_{2} c_{4} + \frac{1}{4} c_{5}) e_{n}^{5} + O (e_{n}^{6}) .

(21)

Now, using (12) and (20) in (18), we get the error equation of method (18) as

\begin{align} e_{n + 1} & = - \frac{1}{9} (a_{1} + a_{2} - 1) (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + \frac{1}{108} (8 (177 a_{1} + 211 a_{2} - 126) c_{2}^{4} \\ - 72 (23 a_{1} + 25 a_{2} - 20) c_{2}^{2} c_{3} + 8 (33 a_{1} + 35 a_{2} - 30) c_{2} c_{4} + 27 (a_{1} + a_{2} - 1) (8 c_{3}^{2} - c_{5})) e_{n}^{5} \\ + \frac{1}{324} (- 8 c_{2}^{5} (2227 a_{1} + 3241 a_{2} - 1165) + 12 c 2^{3} c_{3} (2799 a_{1} + 3595 a_{2} - 1818) \\ - 24 c_{2}^{2} c_{4} (335 a_{1} + 385 a_{2} - 269) - 27 c_{2} (4 c_{3}^{2} (107 a_{1} + 123 a_{2} - 86) \\ + c_{5} (- 51 a_{1} - 55 a_{2} + 45)) + 12 c_{3} c_{4} (207 a_{1} + 215 a_{2} - 198)) e_{n}^{6} + O (e_{n}^{7}) . \end{align}

Therefore, method (18) is of order 6 if

\begin{array}{lll} a_{1} + a_{2} - 1 & = & 0, \\ 8 (177 a_{1} + 211 a_{2} - 126) c_{2}^{4} - 72 (23 a_{1} + 25 a_{2} - 20) c_{2}^{2} c_{3} + 8 (33 a_{1} + 35 a_{2} - 30) c_{2} c_{4} + 27 (a_{1} + a_{2} - 1) (8 c_{3}^{2} - c_{5}) & = & 0, \end{array}\}

whose solution is

a_{1} = \frac{5}{2}

and

a_{2} = - \frac{3}{2}

. Hence, we get a sixth-order method of the form:

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{f (z_{n})}{f^{'} (x_{n})} \cdot (\frac{5}{2} - \frac{3}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) . \end{align}

(22)

Again, using (11) and (21) in Equation (19), we get the error equation of the form:

\begin{align} e_{n + 1} & = - \frac{1}{9} ((- 1 + b_{1} + b_{2}) (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + \frac{1}{108} (8 (- 126 + 143 b_{1} + 109 b_{2}) c_{2}^{4} \\ - 72 (- 20 + 21 b_{1} + 19 b_{2}) c_{2}^{2} c_{3} + 8 (- 30 + 31 b_{1} + 29 b_{2}) c_{2} c_{4} + 27 (- 1 + b_{1} + b_{2}) (8 c_{3}^{2} - c_{5})) e_{n}^{5} \\ + \frac{1}{324} (- 8 (- 1165 + 1349 b_{1} + 607 b_{2}) c_{2}^{5} + 12 (- 1818 + 2051 b_{1} + 1351 b_{2}) c_{2}^{3} c_{3} \\ - 8 (- 807 + 863 b_{1} + 729 b_{2}) c_{2}^{2} c_{4} + 12 (- 198 + 199 b_{1} + 191 b_{2}) c_{3} c_{4} \\ - 27 c_{2} (4 (- 86 + 91 b_{1} + 75 b_{2}) c 3^{2} + (45 - 47 b_{1} - 43 b_{2}) c_{5})) e_{n}^{6} + O (e_{n}^{7}) \end{align}

so that method (19) is of order 6 if

\begin{array}{l} - 1 + b_{1} + b_{2} = 0 \\ 8 (- 126 + 143 b_{1} + 109 b_{2}) c_{2}^{4} - 72 (- 20 + 21 b_{1} + 19 b_{2}) c_{2}^{2} c_{3} + 8 (- 30 + 31 b_{1} + 29 b_{2}) c_{2} c_{4} + 27 (- 1 + b_{1} + b_{2}) (8 c_{3}^{2} - c_{5}) = 0, \end{array}\}

which on solving gives

b_{1} = b_{2} = \frac{1}{2}

. Hence, we get a sixth-order method of the form

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{f (z_{n})}{f^{'} (y_{n})} \cdot (\frac{1}{2} + \frac{1}{2} \frac{f^{'} (x_{n})}{f^{'} (y_{n})}) . \end{align}

(23)

2.4 Eighth-order method

When the fourth-order method is composed with Newton's method, we get

\begin{align} y_{n} & = x_{n} - \frac{2}{3} \frac{f (x_{n})}{f^{'} (x_{n})}, \\ z_{n} & = x_{n} - (- \frac{1}{4} + \frac{3}{4} \frac{f^{'} (x_{n})}{f^{'} (y_{n})} + \frac{1}{2} \frac{f^{'} (y_{n})}{f^{'} (x_{n})}) \cdot \frac{2 f (x_{n})}{f^{'} (x_{n}) + f^{'} (y_{n})}, \\ x_{n + 1} & = z_{n} - \frac{f (z_{n})}{f^{'} (z_{n})} . \end{align}

(24)

Theorem 4.Let f be a real or complex valued function defined on some interval I having sufficient number of smooth derivatives. Let $α$ be a simple root of the equation f(x) = 0. Then method (24) has eighth-order of convergence.

Proof.Taylor's series expansion of $f^{'} (z_{n})$ about $α$ by using (15) gives

\begin{align} f^{'} (z_{n}) & = f^{'} (α) [1 + \frac{2}{9} c_{2} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} - \frac{1}{18} (c_{2} (336 c_{2}^{4} - 480 c_{2}^{2} c_{3} + 72 c_{3}^{2} + 80 c_{2} c_{4} - 9 c_{5})) e_{n}^{5} \\ + \frac{1}{162} (c_{2} (9320 c_{2}^{5} - 21816 c_{2}^{3} c_{3} + + 6456 c_{2}^{2} c_{4} - 2376 c_{3} c_{4} + 27 c_{2} (344 c_{3}^{2} - 45 c_{5})) e_{n}^{6} \\ - \frac{1}{162} (c_{2} (22352 c_{2}^{6} - 74048 c_{2}^{4} c_{3} - 6192 c_{3}^{3} + 29600 c_{2}^{3} c_{4} - 27120 c_{2} c_{3} c_{4} + 2096 c_{4}^{2} \\ + 324 c_{2}^{2} (176 c_{3}^{2} - 25 c_{5}) + 3645 c_{3} c_{5})) e_{n}^{7} + O (e_{n}^{8})] \end{align}

(25)

so that, from (16) and (25), we obtain

\begin{align} \frac{f (z_{n})}{f^{'} (z_{n})} & = \frac{1}{9} (17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4}) e_{n}^{4} + \frac{1}{36} (- 336 c_{2}^{4} + 480 c_{2}^{2} c_{3} - 80 c_{2} c_{4} + 9 (- 8 c_{3}^{2} + c_{5}) e_{n}^{5} \\ + (\frac{2330}{81} c_{2}^{5} - \frac{202}{3} c_{2}^{3} c_{3} + \frac{86}{3} c_{2} c_{3}^{2} + \frac{538}{27} c_{2}^{2} c_{4} - \frac{22}{3} c_{3} c_{4} - \frac{15}{4} c_{2} c_{5}) e_{n}^{6} \\ + \frac{1}{324} (- 22352 c_{2}^{6} + 74048 c_{2}^{4} c_{3} + 6192 c_{3}^{3} - 29600 c_{2}^{3} c_{4} + 27120 c_{2} c_{3} c_{4} - 2096 c_{4}^{2} \\ - 324 c_{2}^{2} (176 c_{3}^{2} - 25 c_{5}) - 3645 c_{3} c_{5}) e_{n}^{7} + \frac{1}{2916} (392972 c_{2}^{7} - 1757952 c_{2}^{5} c_{3} + 870752 c_{2}^{4} c_{4} \\ - 1376244 c_{2}^{2} c_{3} c_{4} + 36 c_{2}^{3} (57299 c_{3}^{2} - 8928 c_{5}) + 27 c_{4} (8836 c_{3}^{2} - 2097 c_{5}) \\ - 6 c_{2} (96066 c_{3}^{3} - 29500 c_{4}^{2} - 50301 c_{3} c_{5})) e_{n}^{8} + O (e_{n}^{9}) . \end{align}

(26)

Applying (15) and (26) in (24), the error equation of method (24) is

e_{n + 1} = \frac{1}{81} c_{2} {(17 c_{2}^{3} - 9 c_{2} c_{3} + c_{4})}^{2} e_{n}^{8} + O (e_{n}^{9}) .

Table 1 collects a comparison of the methods introduced over this section. The comparison is performed in terms of order of convergence (p) and efficiency index ( $E = p^{1 / n_{f}}$ ), where n_f is the number of functional evaluations per iteration. Newton's (1) and Sharma's (4) methods are also included for the sake of comparison, denoted by N and S, respectively. The introduced methods given by (13), (14), (22), (23), and (24) are denoted by M₁, M₂, M₃, M₄, and M₅, respectively.

TABLE 1. Comparison of different methods according to their order of convergence and efficiency

Methods	N	S	M₁	M₂	M₃	M₄	M₅
n_f	2	3	3	4	4	4	5
p	2	4	4	5	6	6	8
E	1.414	1.587	1.587	1.495	1.565	1.565	1.516

3 APPLICATIONS AND EXAMPLES

In this section, numerical tests on the introduced methods are performed. In Subsections 3.1, 3.2, and 3.3 the methods are applied on standard engineering examples.²² Subsection 3.4 covers a set of analytical examples. In all tables, BE(− A) stands for B × 10^−A and M_i, i = 1,2,3,4,5 represent the methods of order 4, 5, 6, 6, and 8, respectively.

3.1 Parachutist's problem

The total force F acting on a falling parachutist is the sum of two opposite forces, namely, the downward force due to gravity F_d and the upward force due to air resistance F_u, so that F = F_d + F_u.

The force due to gravity is given by F_d = mg, where g ≈ 9.8 m/s² is the acceleration due to gravity and m is the mass of the parachutist. Air resistance can be assumed to be linearly proportional to the velocity v and acts in an upward direction, so F_u = −cv, where c is the proportionality constant called the drag coefficient (kg/s) and the negative sign indicates the upward direction. The parameter c is responsible for the properties of the falling object, such as the shape or surface roughness, which affect air resistance. In the case of parachutist, c may be the type of jumpsuit or the orientation used by the parachutist during free-fall.

The total force is obtained as

F = m g - c v .

On the other hand, if a denotes the acceleration, then the second law of motion gives

F = m a = m \frac{d v}{d t}

. Therefore,

\frac{d v}{d t} = g - \frac{c}{m} v

is a differential equation. Assuming that the parachutist is initially at rest, v(t = 0) = 0, its solution is

\begin{align} v (t) & = \frac{g m}{c} (1 - e^{- \frac{c}{m} t}) . \end{align}

(27)

Suppose that it is required to determine the drag coefficient c for a parachutist of a given mass m to attain a prescribed velocity v in a given time period t. Rearranging (27), we get the nonlinear equation

f (c) = \frac{g m}{c} (1 - e^{- \frac{c}{m} t}) - v .

(28)

We assume the values of the parameters as g = 9.8 m/s², m = 68 kg, t = 8 s, and v = 41 m/s. Below, we are applying the introduced iterative methods for solving (28). Initial guess for the drag coefficient is c₀ = 3.0 kg/s The results from first three iterations of each of the methods are presented in Table 2.

TABLE 2. Results for drag coefficient c in the parachutist problem

#Iteration	Results	M₁	M₂	M₃	M₄	M₅
1	c	12.2715	12.4266	12.4616	12.4955	12.5310
	f(c)	0.4859	0.1969	0.1321	0.0695	0.0042
2	c	12.5333	12.5333	12.5333	12.5333	12.5333
	f(c)	3.8857 E(−7)	5.2061 E(−11)	5.6843 E(−14)	0.0	0.0
3	c	12.5333	12.5333	12.53337	12.5333	12.5333
	f(c)	0.0	0.0	0.0	0.0	0.0

3.2 Open-channel flow

An open problem in civil engineering is to relate the flow of water with other factors affecting the flow in open channels such as rivers or canals. The flow rate is determined as the volume of water passing a particular point in a channel per unit time. A further concern is related to what happens when the channel is slopping.

Under uniform flow conditions, the flow of water in an open channel is given by Manning's equation

Q = \frac{\sqrt{S}}{n} A R^{2 / 3},

(29)

where S is the slope of the channel, A is the cross-sectional area of the channel, R is the hydraulic radius of the channel, and n is the Manning's roughness coefficient. For a rectangular channel of width B and water depth in the channel y, it is known that A = By and

R = \frac{B y}{B + 2 y}

. With these values, (29) becomes

Q = \frac{\sqrt{S}}{n} B y {(\frac{B y}{B + 2 y})}^{2 / 3} .

(30)

Now, if it is required to determine the depth of water in the channel for a given quantity of water, (29) can be rearranged as

f (y) = \frac{\sqrt{S}}{n} B y {(\frac{B y}{B + 2 y})}^{2 / 3} - Q .

(31)

In our work, we estimate y when remaining parameters are assumed to be given as Q = 14.15m³/s, B = 4.572 m, n = 0.017, and S = 0.0015. We choose the initial guess y₀ = 3.0m. The results obtained from first three iterations by using the methods M_i,i = 1,…,5, are presented in Table 3.

TABLE 3. Results for the depth water y in the open channel problem

#Iteration	Results	M₁	M₂	M₃	M₄	M₅
1	y	1.4701	1.4656	1.4653	1.4653	1.4650
	f(y)	0.0690	0.0080	0.0038	0.0032	0.0000
2	y	1.4650	1.4650	1.4650	1.4650	1.4650
	f(y)	5.5427 E(−11)	−3.5527 E(−15)	−3.5527 E(−15)	1.7763 E(−15)	1.7763 E(−15)
3	y	1.4650	1.4650	1.46506	1.4650	1.4650
	f(y)	−3.5527 E(−15)	−3.5527 E(−15)	−3.5527 E(− 15)	1.7763 E(−15)	1.7763 E(−15)

3.3 Design of an electric circuit

A common problem in electrical engineering is the study of the steady state behavior of electric circuits. The voltages V_R, V_L and V_C are the potentials across the resistor R, the inductor L, and the capacitor C, respectively. It is known that V_R = iR, $V_{L} = L \frac{d i}{d t}$ , and $V_{C} = \frac{q}{C}$ , where q is the charge and $i = \frac{d q}{d t}$ is the flow of current.

According to Kirchhoff's second law, the algebraic sum of all the voltages around any closed circuit is zero which leads to

L \frac{d i}{d t} + i R + \frac{q}{C} = 0

. Therefore,

L \frac{d^{2} q}{d t^{2}} + \frac{d q}{d t} R + \frac{q}{C} = 0

which is a differential equation whose solution can be obtained as

q (t) = q_{0} e^{- \frac{R t}{2 L}} \cos (\sqrt{\frac{1}{L C} - {(\frac{R}{2 L})}^{2}} t),

(32)

assuming that q(t = 0) = q₀ = V₀C, being V₀ the voltage source.

Let us assume that the appropriate resistor R is required to be determined with known values of L = 5H and C = 10⁻⁴F and C. Moreover, we take $\frac{q}{q_{0}} = 0.01$ , that is, the charge must be dissipated to 1% of its original value in time t = 0.05s. We choose the initial guess for the resistance $R_{0} = 30 Ω$ . The results obtained from first three iterations by using the methods M_i are presented in Table 4.

TABLE 4. Results for the resistor R in the design of an electric circuit

#Iteration	Results	M₁	M₂	M₃	M₄	M₅
1	R	304.7563	314.9646	317.5493	320.8943	327.1815
	f(R)	−0.0243	−0.0134	−0.0107	−0.0073	−0.0009
2	R	328.1494	328.1514	328.1514	328.1514	328.1514
	f(R)	−1.9369 E(−6)	−6.3306 E(−9)	−1.5278 E(−10)	−5.2303 E(−12)	−5.0306 E(−17)
3	R	328.1514	328.1514	328.1514	328.1514	328.15142908514815
	f(R)	3.2959 E(−17)	3.2959 E(−17)	3.2959 E(−17)	3.2959 E(−17)	−5.0306 E(−17)

3.4 Further examples

In this subsection, we study and compare the performance of some of the known methods as well as those obtained in the previous sections on some numerical examples. The methods have been tested on the following functions:

$f_{4} (x) = \sqrt{x^{2} + 2 x + 5} - 2 \sin x - x^{2} + 3,$
$f_{5} (x) = x - 3 \ln x,$
$f_{6} (x) = e^{- x} \sin x + \ln (1 + x^{2}) - 2,$
f₇(x) = (x − 1)³ − 1.

The stopping criteria for the iterative process has been set in $Δ x = | x_{n + 1} - x_{n} | \leq 1 0^{- 12} .$ The details of the work are presented in Table 5. The values displayed are the initial guess x₀, the number of iterations n for achieving the stopping criteria, and the approximated computational order of convergence ACOC.²³ The value NA in ACOC stands for Not Available, because the number of iterates is not enough for its calculation.

TABLE 5. Numerical performance of the introduced methods

Methods		(x₀ = 3.0)	(x₀ = 1.0)	(x₀ = 1.5)	(x₀ = 3.0)
		f₄(x)	f₅(x)	f₆(x)	f₇(x)
N	n	5	7	5	7
	$Δ x$	0.444E − 15	0.0	0.444E − 15	0.0
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.0	0.0	0.0
	ACOC	2.046848	2.000437	1.853573	2.001497
S	n	3	4	3	4
	$Δ x$	0.888E − 15	0.444E − 15	0.444E − 15	0.768E − 13
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.0	0.0	0.0
	ACOC	3.848687	3.202382	3.776679	3.914934
M₁	n	3	4	3	4
	$Δ x$	0.888E − 14	0.0	0.222E − 14	0.111E − 13
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 14	0.0	0.222E − 15	0.0
	ACOC	4.018510	3.702951	4.026750	3.932947
M₂	n	3	4	3	4
	$Δ x$	0.0	0.0	0.0	0.0
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.222E − 15	0.0	0.0
	ACOC	NA	4.601259	NA	3.975725
M₃	n	3	4	3	4
	$Δ x$	0.0	0.0	0.0	0.0
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.222E − 15	0.0	0.0
	ACOC	NA	5.280387	NA	4.486354
M₄	n	3	4	3	4
	$Δ x$	0.0	0.0	0.888E − 15	0.0
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.0	0.222E − 15	0.0
	ACOC	NA	5.495705	NA	4.777322
M₅	n	3	3	3	3
	$Δ x$	0.0	0.444E − 15	0.0	0.4E − 14
	x_n + 1	2.331967655883964	1.857183860207835	2.447748286452425	2.0
	\|f(x_n + 1)\|	0.888E − 15	0.0	0.0	0.0
	ACOC	NA	5.657281	NA	6.827861

4 DYNAMICS OF THE METHODS

In this section, we discuss the dynamics of the methods presented in Section 2 and compare them with some of the existing methods.

4.1 Basics on complex dynamics

Below, some preliminaries of complex dynamics are presented. For further information, see References 21, 24.

For any rational function f(z), a point z₀ is called a fixed point if f(z₀) = z₀. The critical points of f(z) are those points that satisfy $f^{'} (z) = 0$ . The critical points may or may not coincide with the fixed points. Fixed and critical points are not necessarily the roots of f(z) = 0. In this case, they are called strange fixed and free critical points, respectively. A fixed point z₀ of f(z) is superattracting, attracting, repelling or neutral if $f^{'} (z_{0}) = 0$ . $| f^{'} (z_{0}) | < 1$ . $| f^{'} (z_{0}) | > 1$ or $| f^{'} (z_{0}) | = 1$ , respectively.

Let $R : \hat{ℂ} \to \hat{ℂ}$ be a rational function, where $\hat{ℂ}$ is the Riemann sphere. Successive iterations of R over z are called orbits and are given by the sequence {z,R(z),R²(z),R³(z),…}. When iterative methods for solving nonlinear equations are applied on polynomials, they result in a rational function, commonly known as the rational operator. The above considerations for fixed and critical points can be directly extended to rational functions.

4.2 Fixed and critical points

The strange fixed points of any operator may complicate the root finding procedure. If they have an attracting behavior, they may can trap an iteration sequence, giving incorrect results for a z^∗ root of the p(z) polynomial. Even as the repulsive or neutral fixed points, however, they may alter the structure of the basin of attraction for the roots.²⁵ Generally, increasing the order of convergence of any method increases the number of strange fixed points, which may adversely affect the basin of attraction of the method.¹⁶

Corresponding to the Newton's method, define the operator

N (z) = z - \frac{p (z)}{p^{'} (z)},

where p(z) is a polynomial. Similarly, we consider the operators S and M_i(z), i = 1,2,3,4,5 corresponding to the methods M_i, i = 1,2,3,4,5 as defined in Section 2.

4.3 Conjugacy classes

The methods presented in this article verify the Scaling Theorem. By M_ip, we denote the method M_i when applied on the polynomial p(z).

Theorem 5.(Scaling theorem): Let T(z) = az + b, a ≠ 0 be an affine map in the Riemann sphere $\hat{ℂ}$ , and let $λ \in ℂ$ be a nonzero constant. Let p(z) be a polynomial defined in $\hat{ℂ}$ . Define $q (z) = λ (p \circ T) (z)$ . Then

T \circ M_{i q} \circ T^{- 1} = M_{i p},

that is, T is a conjugacy between M_ip and M_iq, where i = 1,2,3,4,5.

Proof.We shall prove the assertion for M₁ only. For other M_i, it can be proved similarly. We have

M_{1 q} (z) = z - [- \frac{1}{4} + \frac{3}{4} \frac{q^{'} (z)}{q^{'} (z - \frac{2}{3} \frac{q (z)}{q^{'} (z)})} + \frac{1}{2} \frac{q^{'} (z - \frac{2}{3} \frac{q (z)}{q^{'} (z)})}{q^{'} (z)}] \frac{2 q (z)}{q^{'} (z) + q^{'} (z - \frac{2}{3} \frac{q (z)}{q^{'} (z)})} .

Since

T^{- 1} (z) = \frac{z - b}{a}

, and

T^{'} (z) = a

, we obtain

\begin{align} T \circ M_{1 q} \circ T^{- 1} (z) & = T \circ M_{1 q} (\frac{z - b}{a}) = a (M_{1 q} (\frac{z - b}{a})) + b \\ = a (\frac{z - b}{a} - \frac{2 p (z) (\frac{3 p^{'} (z)}{4 p^{'} (a (\frac{z - b}{a} - \frac{2 p (z)}{3 a p^{'} (z)}) + b)} + \frac{p^{'} (a (\frac{z - b}{a} - \frac{2 p (z)}{3 a p^{'} (z)}) + b)}{2 p^{'} (z)} - \frac{1}{4})}{a p^{'} (a (\frac{z - b}{a} - \frac{2 p (z)}{3 a p^{'} (z)}) + b) + a p^{'} (z)}) + b \\ = M_{1 p} . \end{align}

Verification of the scaling theorem involves how the methods for a given polynomial relate to the methods for a rescaled polynomial. In other words, we can transform the roots into a related map without qualitatively changing the dynamics of the corresponding methods.^{21, 26}

4.3.1 Corresponding conjugacy class for quadratic polynomials

Newton's method N_p(z) on any quadratic polynomial p(z) is conjugate to the quadratic polynomial z².²¹ Moreover, method S_p(z) is conjugate to $z^{4} \frac{7 + 8 z + 3 z^{2}}{3 + 8 z + 7 z^{2}}$ . In this way, R_N(z) and R_S(z) refer to the application of the Scaling Theorem to N_p(z) and S_p(z), respectively. We show that methods M_ip(z) on quadratic polynomials have more complicated expression for the conjugacy classes. The results are proved in the following theorem.

Theorem 6.Let p(z) = (z − a)(z − b) with a ≠ b, be a quadratic polynomial. Then, the operators M_ip(z) with i = 1, 2, 3, 4, 5 are conjugated to the rational maps R_i(z) with i = 1, 2, 3, 4, 5, respectively. Their expressions are

\begin{array}{l} R_{1} (z) = z^{4} \frac{9 z^{2} + 18 z + 17}{17 z^{2} + 18 z + 9}, \\ R_{2} (z) = z^{5} \frac{243 z^{7} + 1296 z^{6} + 3672 z^{5} + 6624 z^{4} + 7959 z^{3} + 6196 z^{2} + 2790 z + 612}{612 z^{7} + 2790 z^{6} + 6196 z^{5} + 7959 z^{4} + 6624 z^{3} + 3672 z^{2} + 1296 z + 243}, \\ R_{3} (z) = z^{6} \frac{918 + 4032 z + 8843 z^{2} + 11560 z^{3} + 10081 z^{4} + 6048 z^{5} + 2493 z^{6} + 648 z^{7} + 81 z^{8}}{(9 + 18 z + 17 z^{2}) (9 + 54 z + 152 z^{2} + 266 z^{3} + 301 z^{4} + 180 z^{5} + 54 z^{6})}, \\ R_{4} (z) = z^{6} \frac{243 z^{6} + 972 z^{5} + 2484 z^{4} + 4068 z^{3} + 4671 z^{2} + 3160 z + 1122}{(17 z^{2} + 18 z + 9) (66 z^{4} + 116 z^{3} + 117 z^{2} + 54 z + 27)}, \\ R_{5} (z) = z^{8} \frac{{(9 z^{2} + 18 z + 17)}^{2}}{{(17 z^{2} + 18 z + 9)}^{2}} . \end{array}

Proof.We prove the result for M₁(z) only. The rest of cases can be proved similarly.

Consider the Möbius transformation $h : \hat{ℂ} \to \hat{ℂ}$ given by $h (z) = \frac{z - a}{z - b} .$ Note that $h^{- 1} (z) = \frac{b z - a}{z - 1}$ . Then

(h \circ M_{1} \circ h^{- 1}) (z) = z^{4} \frac{9 z^{2} + 18 z + 17}{17 z^{2} + 18 z + 9} = R_{1} (z) .

4.4 Basins of attraction

The basins of attraction of any rational operator R(z) explain the dynamical behavior of the methods. If z^∗ is an attracting fixed point of the rational operator R(z), then the basin of attraction of z^∗ is the set

ℬ (z^{*}) = {z \in \hat{ℂ} : R^{n} (z) \to z^{*} as n \to \infty} .

Since the Möbius transform can be performed for quadratic polynomials, we are studying their behavior. Regarding cubic polynomials, the analysis is performed in terms of different cubic polynomials.

In our work, we use Mathematica 9.0 for the symbolic calculations, while the representations of the basins of attraction, that follows the guideline of Reference 27, are performed with Matlab R2017b. We divide the complex plane into 500 × 500 initial points in the domain $[- 3, 3] \times [- 3, 3]$ to determine the basins of attraction of the roots of the polynomials. Each root of the polynomial is mapped to a different color. If an initial guess tends to a root of the polynomial, this point is represented with its corresponding color. Indeed, the dynamical planes include information about the number of iterations required to converge to the root: the more iterations required, the darker color.

4.4.1 Dynamical analysis applying the methods on quadratic polynomials

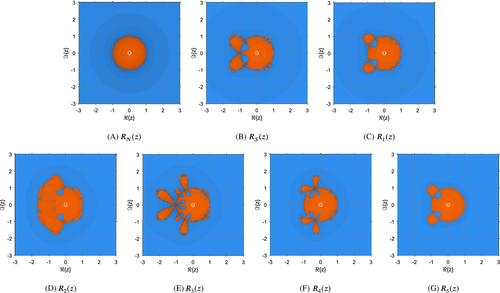
The rational maps of Theorem 6 correspond to the rational functions of the introduced methods when they are applied to quadratic polynomials. In every case, $z_{1}^{*} = 0$ is a superattracting fixed point. As introduced in Reference 14, $z_{2}^{*} = \infty$ is also a superattracting fixed point. The rest of fixed points are repelling, improving the stability of the method. The number of fixed and critical points is displayed in Table 6.

TABLE 6. Number of extraneous fixed points (#EFP) and free critical points (#FCP) for different rational functions when a quadratic polynomial is applied

Method	N(z)	S(z)	R₂(z)	R₃(z)	R₄(z)	R₅(z)	R₆(z)
#EFP	1	5	5	11	13	11	11
#FCP	0	3	4	14	13	8	6

Since every strange fixed point is repelling, their presence does not affect negatively to the stability of the corresponding methods. In order to verify this fact, and also to analyze the shape and width of the basins of attraction, Figure 1 represents the dynamical planes of the introduced methods. Note that the orange color is devoted to the root $z_{1}^{*} = 0$ and the blue one corresponds to the superattracting point $z_{2}^{*} = \infty$ .

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Dynamical planes of several methods for quadratic polynomials

4.4.2 Dynamical analysis applying the methods on cubic polynomials

When the rational functions are applied on cubic polynomials, the resulting expressions are in terms of the original method instead of using their Möbius transform. In order to analyze a complete behavior over the cubic polynomials, the iterative methods are applied on p_•(z) = z³, p₊(z) = z³ + z, and p₋(z) = z³ − z, as performed in Reference 28.

In the p_•(z) case, there is no presence of fixed points, but the root $z_{1}^{*} = 0$ , that is, superattracting, and the z₂ = ∞, whose behavior is repelling.

When the polynomial p₊(z) is applied, the roots $z_{0}^{*}$ and $z_{3 - 4}^{*} = \pm i$ are superattracting points. As in the previous polynomial, the point z₂ = ∞ is a repelling point. In this case, there is a big presence of extraneous fixed points, but they behave in a repelling way.

Finally, the application of the methods on the polynomial p₋(z) gives a similar performance than in the p₊(z) case. The roots $z_{0}^{*} = 0$ and $z_{5 - 6}^{*} = \pm 1$ are superattracting, the point z₂ = ∞ is repelling, and the rest of strange fixed points are also repelling. Table 7 gathers the information about the extraneous fixed points and free critical points when the three polynomials are applied on the introduced methods.

TABLE 7. Number of extraneous fixed points (#EFP) and free critical points (#FCP) for different rational functions when a cubic polynomial is applied

p(z)	Method	S(z)	R₂(z)	R₃(z)	R₄(z)	R₅(z)	R₆(z)
p_•(z)	#EFP	0	0	0	0	0	0
	#FCP	0	0	0	0	0	0
p₊(z)	#EFP	12	12	42	48	42	42
	#FCP	12	18	44	48	42	42
p₋(z)	#EFP	12	12	42	48	42	42
	#FCP	12	18	44	48	44	22

Figures 2-4 represent the dynamical planes of the introduced methods. In Figure 2 a unique basin of attraction can be observed, due to the polynomial p_•(z) = z³ has only a superattracting point in $z_{1}^{*} = 0$ . Therefore, every initial guess whose orbit tends to this root is represented in orange.

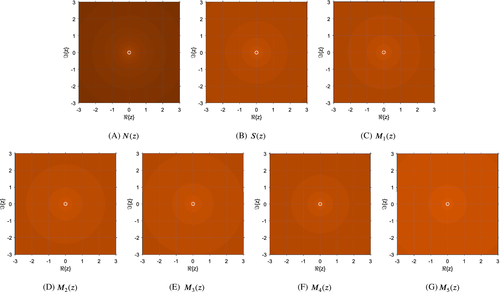
The stability of every method, when they are applied on p_•(z), is verified in the complete plane, as pictured in Figure 2. Note that every initial guess in the complex plane tends to the superattracting point $z_{1}^{*} = 0$ .

Figure 3 illustrates the dynamical planes of methods M_1 − 5(z) when they are applied on p₊(z) = z³ + z. In this case, there are three superattracting points: $z_{0}^{*}$ is mapped to color orange, $z_{3}^{*} = i$ is mapped to color blue, and $z_{4}^{*} = - i$ is mapped to color green.

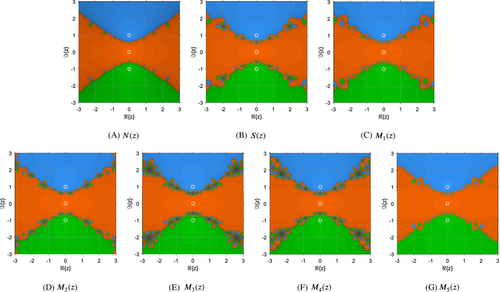
The dynamical planes of Figure 3 confirm the theoretical analysis. There is not any fixed point different to the roots that attracts any orbit. All initial estimates tend to one of the three superattracting points, showing the wide region of stability of every method. The methods of order 6 show a more intricated Julia set than the other ones. However, when the order is increased, this behavior is not observed. The composition with Newton's method makes the borderlines of the dynamical planes smoother.

Finally, Figure 4 represents the dynamical planes of the methods when they are applied on p₋(z) = z³ − z. In this case, the orange basin remains with $z_{1}^{*} = 0$ , while blue and green basins are referred to $z_{5}^{*} = 1$ and $z_{6}^{*} = - 1$ , respectively.

The features of Figure 4 coincide with Figure 3 corresponding ones. Note that the planes of Figure 4 are just a rotation of the planes of Figure 3.

5 CONCLUSIONS

A new set of iterative methods, based on Weerakoon and Fernando method, have been introduced. These methods, of different orders of convergence, have been checked by numerical and stability tests. On the one hand, the numerical performance makes evident the power of these methods, as they all converge to the expected root and reduce the number or iterations compared with Newton's method. On the other hand, the stability analysis, carried out in terms of complex dynamics, shows that every initial guess tends to a superattracting point that matches with the root of the corresponding polynomial. This fact is due to the absence of strange fixed points that behave attracting in both quadratic and cubic polynomials.

ACKNOWLEDGEMENTS

This research was supported by PGC2018-095896-B-C22 (MCIU/AEI/FEDER/UE).

CONFLICT OF INTEREST

The authors declare no potential conflict of interests.

Biographies

Prem B. Chand is a PhD candidate in the Department of Mathematics, South Asian University, New Delhi, India. He is a professor of Mathematics in National Academy of Science and Technology (Pokhara University), Nepal. His current research is concerned with Numerical Analysis and Scientific Computing. He is author of more than four research articles in the field of numerical analysis and computing.
Francisco I. Chicharro received his PhD in mathematics in 2017 and his PhD in telecommunications in 2018, both at Universitat Politècnica de València, Spain. He is the head of the Computational Mathematics Degree at Universidad Internacional de La Rioja UNIR, Spain. He is author of more than 20 research articles covering the areas of computational mathematics and optical transmission of OFDM signals.
Pankaj Jain is a Professor of Mathematics at South Asian University, New Delhi, India. His research interests include numerical analysis, Fourier analysis, function spaces, weighted norm inequalities and applications of these areas. He has published over 75 research articles in these areas.

References

1Weerakoon S, Fernando TGI. A variant of Newton's method with accelerated third-order convergence. Appl Math Lett. 2000; 13: 87-93.
10.1016/S0893-9659(00)00100-2
Web of Science® Google Scholar
2Kung HT, Traub JF. Optimal order of one-point and multipoint iterations. J Assoc Comput Mach. 1984; 21: 643-651.
10.1145/321850.321860
Web of Science® Google Scholar
3 Ostrowski AM. Solutions of Equations and System of Equations. Cambridge, MA: Academic Press; 1960.
Google Scholar
4 Petković MS, Neta B, Petković LD, Džunić J. Multipoint Methods for Solving Nonlinear Equations. Amsterdam, The Netherlands: Elsevier; 2013.
Google Scholar
5 Traub JF. Iterative Methods for the Solution of Equations. Upper Saddle River, NJ: Chelsea; 1977.
Google Scholar
6Artidiello S, Cordero A, Torregrosa JR, Vassileva MP. Design and multidimensional extension of iterative methods for solving nonlinear problems. Appl Math Comput. 2017; 293: 194-203.
Web of Science® Google Scholar
7Babajee DKR. Several improvements of the 2-point third order midpoint iterative method using weight functions. Appl Math Comput. 2012; 218: 7958-7966.
Web of Science® Google Scholar
8Chun C, Neta B, Kozdon J, Scott M. Choosing weight functions in iterative methods for simple roots. Appl Math Comput. 2014; 227: 788-800.
Web of Science® Google Scholar
9Sharma R, Bahl A. An optimal fourth order iterative method for solving nonlinear equations and its dynamics. J Complex Anal. 2015; 259167: 1-9.
Google Scholar
10Amiri A, Cordero A, Darvishi MT, Torregrosa JR. Stability analysis of a parametric family of seventh-order iterative methods for solving nonlinear systems. Appl Math Comput. 2018; 323: 43-57.
Web of Science® Google Scholar
11Chicharro FI, Cordero A, Garrido N, Torregrosa JR. Generalized high-order classes for solving nonlinear systems and their applications. Mathematics. 2019; 1194: 1-14.
Google Scholar
12Chicharro FI, Cordero A, Torregrosa JR. Dynamics of iterative families with memory based on weight functions procedure. J Comput Appl Math. 2019; 354: 286-298.
10.1016/j.cam.2018.01.019
Web of Science® Google Scholar
13Argyros IK, Cordero A, Magreñán ÁA, Torregrosa JR. Third-degree anomalies of Traub's method. J Comput Appl Math. 2017; 309: 511-521.
10.1016/j.cam.2016.01.060
Web of Science® Google Scholar
14Chicharro FI, Cordero A, Gutiérrez JM, Torregrosa JR. Complex dynamics of derivative free methods for nonlinear equations. Appl Math Comput. 2013; 219: 7023-7035.
Web of Science® Google Scholar
15Cordero A, Feng L, Magreñán ÁA, Torregrosa JR. A new fourth order family for solving nonlinear problems and its dynamics. J Math Chem. 2015; 53: 893-910.
10.1007/s10910-014-0464-4
CAS Web of Science® Google Scholar
16Neta B, Chun C. Basins of attractions for several methods to find the simple roots of nonlinear equations. Appl Math Comput. 2012; 218: 10548-10556.
Google Scholar
17Sharma JR, Arora H. A new family of optimal eighth order methods with dynamics for nonlinear equations. Appl Math Comput. 2016; 273: 924-933.
Web of Science® Google Scholar
18 Alexander DS. A History of Complex Dynamics: From Schröder to Fatou and Julia. Des Moines, IA: Friedr & Sohn Veriage; 1994.
10.1007/978-3-663-09197-4
Google Scholar
19Argyros IK, Magreñán ÁA. Iterative Methods and Their Dynamics with Applications: A Contemporary Study. Boca Raton, FL: CRC Press; 2016.
Google Scholar
20Beardon AF. Iteration of Rational Functions. New York, NY: Springer-Verlag; 1991.
10.1007/978-1-4612-4422-6
Google Scholar
21Blanchard P. The dynamics of Newton's method. Proc Symp Appl Math. 1994; 49: 139-154.
10.1090/psapm/049/1315536
Google Scholar
22 Chapra SC, Canale RC. Numerical Methods for Engineers. Medford, MA: McGraw Hill; 2015.
Google Scholar
23Cordero A, Torregrosa JR. Variants of Newton's method using fifth order quadrature formulas. Appl Math Comput. 2007; 190: 686-698.
Web of Science® Google Scholar
24 Devaney RL. An Introduction to Chaotic Dynamical Systems. Boston, MA: Addison-Wesley; 1989.
Google Scholar
25Vrscay ER, Gilbert WJ. Extraneous fixed points, basin boundaries and chaotic dynamics for Schröder and König rational iteration functions. Numer Math. 1988; 52: 1-16.
10.1007/BF01401018
Web of Science® Google Scholar
26Carleson L, Gamelin TW. Complex Dynamics. New York, NY: Springer-Verlag; 1992.
Google Scholar
27Chicharro FI, Cordero A, Torregrosa JR. Drawing dynamical and parameters planes of iterative families and methods. Sci World J. 2013; 780153: 1-11.
10.1155/2013/780153
Web of Science® Google Scholar
28Amat S, Busquier S, Plaza S. Chaotic dynamics of a third-order Newton-type method. J Math Anal Appl. 2005; 366: 24-32.
10.1016/j.jmaa.2010.01.047
Web of Science® Google Scholar

Citing Literature

All articles

On the design and analysis of high-order Weerakoon-Fernando methods based on weight functions

Abstract

1 INTRODUCTION

2 DEVELOPMENT OF METHODS AND THEIR CONVERGENCES

2.1 Fourth-order method

2.2 Fifth-order method

2.3 Sixth-order method

2.4 Eighth-order method

3 APPLICATIONS AND EXAMPLES

3.1 Parachutist's problem

3.2 Open-channel flow

3.3 Design of an electric circuit

3.4 Further examples

4 DYNAMICS OF THE METHODS

4.1 Basics on complex dynamics

4.2 Fixed and critical points

4.3 Conjugacy classes

4.3.1 Corresponding conjugacy class for quadratic polynomials

4.4 Basins of attraction

4.4.1 Dynamical analysis applying the methods on quadratic polynomials

4.4.2 Dynamical analysis applying the methods on cubic polynomials

5 CONCLUSIONS

ACKNOWLEDGEMENTS

CONFLICT OF INTEREST

Biographies

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the design and analysis of high-order Weerakoon-Fernando methods based on weight functions

Abstract

1 INTRODUCTION

2 DEVELOPMENT OF METHODS AND THEIR CONVERGENCES

2.1 Fourth-order method

2.2 Fifth-order method

2.3 Sixth-order method

2.4 Eighth-order method

3 APPLICATIONS AND EXAMPLES

3.1 Parachutist's problem

3.2 Open-channel flow

3.3 Design of an electric circuit

3.4 Further examples

4 DYNAMICS OF THE METHODS

4.1 Basics on complex dynamics

4.2 Fixed and critical points

4.3 Conjugacy classes

4.3.1 Corresponding conjugacy class for quadratic polynomials

4.4 Basins of attraction

4.4.1 Dynamical analysis applying the methods on quadratic polynomials

4.4.2 Dynamical analysis applying the methods on cubic polynomials

5 CONCLUSIONS

ACKNOWLEDGEMENTS

CONFLICT OF INTEREST

Biographies

References

Citing Literature

Figures

References

Related

Information