Abbreviations: CPA, chosen plaintext attack; DL, deep learning; FHE, fully homomorphic encryption; ML, machine learning; NN, neural network; OPE, order-preserving encryption; PPE, property preserving encryption.

About

Sections

PDF

Tools

Share a link

Email
Wechat
Bluesky

Abstract

Big data environments have become a standard solution in most public and private corporations since they allow the acquisition and processing of massive volumes of heterogeneous data, and also, act as enablers to extract useful information and insights from this data to optimize internal and external operations in these businesses. As big data tools evolve and become commodities, their democratization process helped promote new industries, business models, companies, and all sorts of new features to improve our way of life. On the other hand, the demand for flexible and powerful privacy schemes for big data has also increased, and it is now an active area of research, with different approaches to the initial problem being taken until now. In this document, we will review some of the most notorious ones, such as trying to preserve various mathematical properties in ciphertexts or using neural network-based solutions for different parts of the encryption process, allowing interesting features in the cryptographic scheme by construction. Privacy individual and social concerns of potential misuses of big data, as the primary root cause for this demand, also pose an opportunity for Cryptography to propose adaptation of standard solutions, as well as new, tailored ones for these environments. The latter should allow the proposals to tackle the specific needs of each individual big data application while addressing privacy issues in a standardized way. Finally, though it is usually considered that cryptographic schemes for big data environments are inherently resource intensive by construction, it can be seen that there are clear opportunities for efficiency improvements in current solutions for different tasks that do not require complex algorithms to be applied over encrypted space. In this document, we discuss and evaluate potential improvements in some cryptographic schemes for various tasks of different nature, considering the implications over big data setups, and deriving some open questions and possible research directions on different fields of interest.

1 INTRODUCTION

It is widely acknowledged that the number of areas in which technology is present every day has greatly increased in the last decades at an impressive pace, and it is expected to continue growing in the next years toward regular aspects of human life.1 If it can easily be seen that the ubiquitous presence of these technologies provide numerous advantages for society, businesses, and individuals, it also poses a number of challenges difficult to tackle. Among those, there has been a recent serious social concern in individual privacy and security ones.2-4

It is specially noticeable the paradigm shift in the area of big data applications, where the amount of data collected and operated by businesses has greatly increased from very heterogeneous sources,1 as the diagram in Figure 1 outlines. Classic solutions for processing data and protecting it have been tried to be adapted to overcome the challenges posed by this shift, with different outcomes.5-7

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A myriad of services now contribute to the massive data volumes currently gathered

New challenges can arise though, such as the need for data querying, processing and modeling techniques (eg, machine learning (ML) algorithms) to be applied over encrypted spaces rather than plaintext ones for enforcing privacy of subjects behind the data.8-11 Implications from these challenges can be derived from the fact that standard current techniques make use of linear algebra for their operations, and therefore encrypted spaces must preserve the necessary mathematical space properties in each task considered so that the corresponding current technique can be also applied over ciphertexts.8, 11, 12

Nonetheless, though it is widely believed that cryptographic solutions for big data environments do not pose serious challenges over complexity, which is commonly taken as potentially large enough for any proposed implementation, the trade-off between security and complexity can be shown that it is still important,6, 13 and most common applications in big data do not have the aforementioned specific needs, and cryptographic proposals can adapt their complexity without generally reducing security bounds, improving their usability and applicability accordingly.

The rest of this paper is distributed as follows. Section 2 reviews some of the state-of-art solutions in privacy preserving encryption (PPE) family of schemes, focusing on the solutions specially tailored to big data needs and characteristics, such as order-preserving encryption (OPE), or fully homomorphic encryption (FHE) schemes. Section 3 surveys the state-of-art in neural cryptography, where it is specially noticeable the recent advances in the subfield of adversarial neural computing. On the other hand, Section 4 describes the experimental work to compare the practical implications of some cryptographic schemes being applied over several datasets of different size and provide some insights on how these implications could be extrapolated to big data environments. Finally, Section 5 summarizes some conclusions from the work and outlines some possible future lines of research.

2 PROPERTY PRESERVING ENCRYPTION

One of the most widely accepted advantages of big data tools is the ability to customize them and adapt their workflow to best suit specific needs of each individual application. The same expectation could apply to the cryptographic schemes that aim to preserve the security and privacy of the implemented solutions. In practice, tailoring the cryptographic solution to the big data end task means accounting for the algorithm, or family of algorithms, to be applied over the data to extract the desired information. Applying different ML techniques or performing searches over the data can be two examples of these algorithms.

Many techniques, including those cited previously, apply linear algebra to get a suitable result. For that reason, the application of the same algorithms over encrypted data, and obtaining the same result as in the plaintext one, pose the need for specific mathematical properties to be preserved in both spaces.

Property Preserving Encryption14 refers a family of encryption schemes in which the encrypted data preserve a specific property in the encrypted space. Some examples of mathematical properties preserved could be equality,15 numerical ordering,16, 17 (in the following section, OPE schemes will be analyzed in detail), or a specific operation (eg, addition, multiplication).18, 19

In PPE proposals, system security is aimed to be preserved in the same way as other cryptographic schemes, but by preserving a certain mathematical property of interest, some other algorithms can be applied over encrypted space and therefore preserve privacy of subjects in the dataset.14 Nonetheless, security assessment of PPE solutions must include the analysis of implications of information leaking to potential attackers, at least any leakage from the preserved property by design.20, 21

On the other hand, there are also active research efforts to broaden the scope of conditions in which security analysis is to be performed.22 They usually show that current proposals can only be applied over the restrictive conditions for which they were initially designed, but generalizations usually come at the cost of lowering security bounds and proofs accordingly.22

2.1 Order-preserving encryption

One of the most widespread applications of big data tools is the democratization of querying tools over larger volumes of data. This application generalizes previous technical systems that were constrained on the amount of information they were capable to handle. Therefore, a direct adaptation to big data environments pose the need to preserve ordering of samples if an encryption scheme is to be used for this task.

An OPE scheme16, 17 is one that provided [x] is the encrypted version of x, then for all possible x and y,

[x] > [y] iff x > y .

(1)

OPE schemes are based on ONE-WAYNESS theorem,23 with two different definitions:

– (r, z)-WOW (Window One-Wayness)23: it states that no adversary, given z uniformly randomly selected ciphertexts, is able to limit at least one of the underlying plaintexts to an interval of range r.
– (r, z)-WDOW (Window Distance2 One-Wayness)23: no adversary, given z uniformly randomly selected ciphertexts, is able to find an interval of range r in which the distance of any pair of plaintexts lies.

The definitions earlier are important since, in a regular database setting, the size for which an attacker could breach the database by getting all ciphertext in it is calculated (r). Nonetheless, the same definitions do not ensure anything about the secrecy of internal plaintext partial information.24

Proof for one-wayness theorems is provided in the work of Boldyreva et al17 for uniformly distributed variables, but the proof is not valid for nonuniformly distributed ones, as demonstrated in the works of Durak et al22 and Naveed et al.25 The effects over nonuniform distributions are unwanted leakage to attackers when specific attacks are proposed.22 Figure 2 shows how unwanted leakage can be exploited to obtain fine-grained original information.

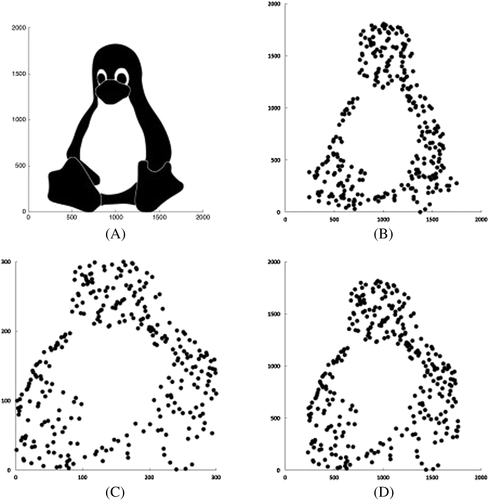
Furthermore, Figure 3 also shows unwanted leakage of information related to distance-based calculations. An adversarial can reduce the query error by several orders of magnitude in specific attacks by restricting the possible locations of data points (in the figure, road intersections cannot be placed in the sea), and by joining query results with publicly available information (eg, administrative borders).22

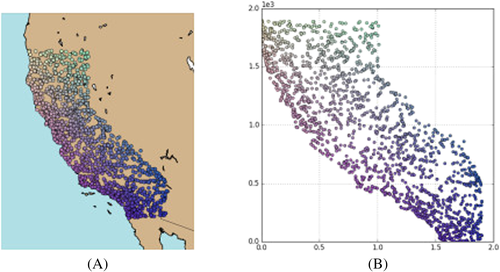
On the other hand, intra and intervariable correlation can be also exploited to leak more information to attackers, by using proxy variables also present in the dataset to restrict the ordering ranges of the encrypted variables, and consequently reducing entropy over the original information. 22, 26

It can be generically shown that, for a security notion of OPE such as indistinguibility under ordered Chosen Plaintext Attacks (CPA), any OPE can be broken with overwhelming probability if the OPE size has superpolynomial size message space (for polynomial size message space OPE, security bounds make schemes lose practical utility).24

Finally, OPE schemes are shown to be inherently leaky methods, and security bounds have not yet been standardized, though several proposals have been made in this direction.24 On the other hand, OPE has also proven to be one of the most promising cryptographic schemes used in encrypted database processing, and even some commercial applications have been deployed.8, 27 It is expected that this field of research continues to evolve, enforcing security guarantees while retaining application usefulness.

2.2 Fully homomorphic encryption

One of the consequences of the rise of big data environments was the evolution of previous ML algorithms, specially those based over neural networks (NN). More powerful networks, such as deep learning (DL) ones, rely on increasing NN complexity by raising the number of layers (each of them could be seen as single NNs being used sequentially), which can be trained together, increasing total expressive power of the whole algorithm. The dramatic increase of the uses of DL techniques, empowered by the evolution of big data tools, have also posed the challenge on how to apply these networks (inherently nonlinear functions) over encrypted spaces, as in the case of database processing for OPE schemes.

In order to address this challenge, Gentry proposed an FHE scheme.18, 19 A scheme is additively and multiplicatively homomorphic, respectively, if provided [x] is the ciphertext of x, then18

[x + y] = [x] \oplus [y]

(2)

[x \cdot y] = [x] \otimes [y] .

(3)

The FHE schemes fulfill both conditions.18 After this seminal work, which was deemed inefficient to be implemented in commercial applications,28 many efforts have been made to apply FHE in a more efficient way, some potentially quantum-resistant.29, 30

A problem with FHE proposals is derived from the vanishing gradient problem.31 This means that, for very deep NNs, trainable parameters for deeper layers are less impacted by error backpropagation training, and therefore these layers cannot be significantly trained after some depth. Regarding cryptographic schemes, the counterpart implication is that information can be significantly leaked (therefore limiting data privacy) for the cited deeper layers in the same networks.31 For that reason, leveled homomorphic encryption schemes were proposed instead, in which computation is allowed up to a predefined depth.31

On the other hand, FHE schemes inherently leaks much information, since by leaking arithmetic properties such as addition and multiplication, a lot of derived information can also be available. Furthermore, a deep analysis on the impact of FHE over nonuniform probability distributions could arise more serious concerns about unwanted leaks over specific attacks, continuing the work of Berkoff et al in leakage-resilient proposals.32

3 NEURAL CRYPTOGRAPHY

In this review, it has already been discussed the rise of NNs mainly for ML tasks (eg, classification, regression, clustering…). This popularity is due to the fact that NNs serve in practice as universal function approximators,33 as their expressive power has been increased by new training algorithms34 and layering techniques (ie, DL).35 The same property can be used for cryptography tasks, leading to the rising trend of neural cryptography.36

An NN37 is, in fact, a two-stage classification or regression scheme, which can be seen in Figure 4 in its most typical state. First layer represents the different inputs provided to the network, x_i. Last layer represents the K outputs of the system, each represented as y_k, and represent the generic Y=f(X_i) function to be approximated, where

Y \in R^{K}

. Finally, a single HIDDEN layer is also represented in the figure, where

z_{m} = σ (ω_{0 m} + \sum_{i} ω_{i m} x_{i}) .

(4)

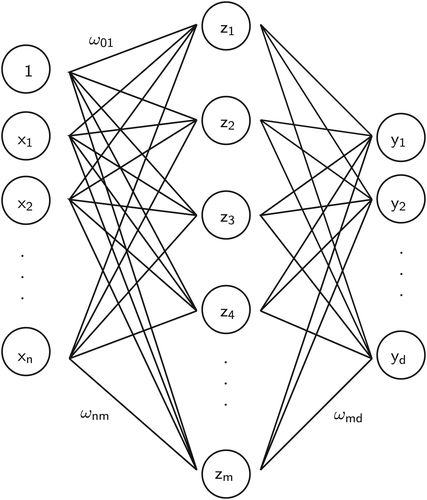
In Equation 4, each hidden NEURON (each z_m) is a nonlinear combination (here represented by σ) of training weights (ω_im) multiplied by each input. Generically, every neuron is connected to every input, and every output is connected to every neuron, providing a fully connected feedforward NN38(because there are no backward connections). Nonlinear functions typically used in NNs are sigmoid or hyperbolic tangent functions, due to the fact that their first derivative exists for working ranges.

The NNs have been successfully applied to different tasks related to cryptography: pseudo-random number generator,39 steganography,40 deploying predictive systems,41, 42 learning data-driven privacy schemes,43 etc. These exercises have proven that NNs can be used for different tasks and are flexible enough to be used in a myriad of different ways. It is specially important the case of FHE-based encryption schemes,41 where the use of nonlinear functions could be seen as contradictory with FHE schemes as presented in Section 2. Nonetheless, nonlinear functions can be approximated by polynomials, allowing FHE schemes to be implemented,44, 45 so FHE encryption and deep NNs can be jointly used to provide ML tasks over encrypted spaces.45

On the other hand, NN-based implementations are computationally complex (typically $O (N^{3})$ ), so long training times are common in these schemes, even with graphics processing unit (GPU) processors, which reduce these training times greatly. Furthermore, NNs are usually trained as encoder-decoder schemes together, so decoding network is usually provided as key to the encryption system. As a result, both training times and key size are infeasible for many nowadays applications.

An interesting research line is the use of echo state networks (ESNs) for encryption purposes.46 The ESN is a simple recurring network that, when used as encoding scheme, has been proven to provide confusion and diffusion properties,46 which can be defined as:

– Confusion: each bit of the ciphertext should depend on several parts of the key, obscuring the connections between the two.
– Diffusion: if we change a single bit of the plaintext, then (statistically) half of the bits in the ciphertext should change (and vice versa).

Using ESN as encryption schemes, with some improvements also proposed in the same work,46 could lead to lower overall system complexity, but it still serves as an intellectual exercise more than a proposal that would be widely implemented.

Regarding security concerns about the use of neural cryptography in widespread applications, NNs can be seen as black boxes between inputs and outputs. Obscuring encryption algorithm by using a black box algorithm is usually considered to lack security guarantees, so the system can be considered insecure from this point of view by design.47 Furthermore, a discussion on designing ML pipelines compliant with security and privacy standards48 opens the question of how to design the next generation of predictive techniques with cryptographic solutions embedded, which impacts the use of neural cryptography as a clear possibility for being part of these techniques.

3.1 Adversarial neural cryptography

Abadi et al introduced the use of NNs for encrypting messages,49 providing a seminal work on adversarial neural criptography. In this work, a scheme of encoding and decoding networks is also proposed, together with an adversarial network, which provide the inclusion of mathematical terms for eavesdroppers or attackers in the optimization function.49 The proposed scheme by Abadi et al,49 which can be seen in Figure 5, defines the problem in which Alice wants to send an encrypted message to Bob, which aims to decrypt the message correctly. For that matter, a key is shared between Alice and Bob as it is standard in cryptographic schemes. On the other hand, Eve aims to also decrypt the ciphertext without the key, but the training goal for Eve is to be able to correctly decrypt 50% of the bits in the ciphertext (if Eve decrypted less than 50% of the bits correctly, she could switch all bits to obtain a higher accuracy decryption rate).

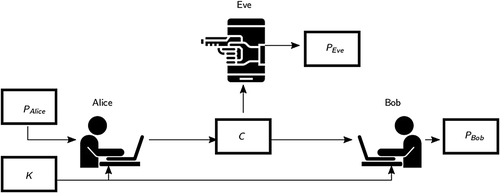
It is important to note that, since this first seminal work, a number of proposals have also applied adversarial neural cryptography to different tasks.39, 43 Nonetheless, as stated by Muñoz et al,47 we are in a very early stage of maturity in this field, lacking practical implementations of such cryptographic schemes that could be of much use in different applications.

Analyzing adversarial setups for cryptographic schemes, the inclusion of attackers in the optimization model can lead to interesting results in terms of robustness against these attacks.49 Nonetheless, serious concerns have been raised over the guarantees provided by these setups over practical attacks, as they will probably be carried out by physical entities, and statistical robustness provides only limited protection against specific, targeted attacks over individual vulnerabilities.47

On the other hand, the practical limitations of neural cryptography also apply to adversarial setups, which also pose some important challenges for future works to overcome, and more research efforts are needed to evolve these first proposals in the field into mature setups to be widely used.

4 EXPERIMENTAL RESULTS

As part of this state-of-art review, one of the most widely accepted assumptions when proposing cryptographic schemes for big data environments is that computational resources are not a restriction to the proposal, which, in practice, considers them as unlimited. That leads to avoid the trade-off between security and complexity. We aim to illustrate the implications of this assumption and claim that the impact on efficiency in final designs make some of the solutions very difficult to be standardized and deployed in practical environments.

4.1 Datasets

One of the common gaps between academic works and practical implementations is the nature of the datasets in which proposals are tested. We propose to tackle this problem by using three different datasets from DATA SCIENCE FOR GOOD series, hosted by KAGGLE corporation.3 A brief description of each dataset is as follows.4

– PASSNYC: PASSNYC is a not-for-profit organization for broadening educational opportunities for New York City talented and underserved students. Dataset aims to identify the potential of each school to improve the chances of their students receiving places in specialized high schools.
– Kiva: Kiva.org is an online crowdfunding platform to extend financial services to poor and financially excluded people around the world. Dataset aims to estimate the welfare level of borrowers in different regions and connect it to loan features.
– CPE: Center for Policing Equity is a public US institution aiming to use Data Science tools to bridge the divide created by communication problems, suffering and generational mistrust, and forge a path toward public safety, community trust, and racial equity. Dataset tries to address racial fairness issues in certain areas, so other agencies can deploy measures to improve this aspect.

In order to fairly compare performance of different algorithms, we chose four different features from each dataset, being two of them numeric and the other two string based. We chose features that vary in range and precision for numeric values, and field length and categorical or free text in string-based ones.

On the other hand, for each algorithm to be able to encrypt data, restrictions over variable nature are applied, and numeric features can be converted to strings if needed. Some other specific details of the setup for all datasets can be found in Table 1, and some examples of the data used in the analysis are shown in Table 2.

Table 1. Properties of used datasets

Dataset	Samples	Features	Owner	Numeric	String
				Selected variables
PASSNYC	1272	161	PASSNYC	% Asian, % Hispanic	School name, Full address
Kiva	671205	20	Kiva.org	Funded amount, Term (months)	Use, Region
CPE	710472	12	Center for Policing Equity	Latitude, Longitude	Driver race, Driver gender

Table 2. Example of each variable used per dataset

Dataset	Variable	Examples
PASSNYC	% Asian	5%
	% Hispanic	60%
	School Name	P.S. 015 ROBERTO CLEMENTE
	Full address	333 E 4TH ST NEW YORK, NY 10009
Kiva	Funded amount	575
	Term (months)	11
	Use	To repair their old cycle-van and buy another one to rent out as a source of income
	Region	Lahore
CPE	Latitude	44.973917
	Longitude	-93.060895
	Driver race	White
	Driver gender	Female

4.2 Experimental setup

Experiments were carried out on a Intel Core i7-8550U 1.80GHz quad-core desktop workstation. Readily available Python-based implementation of the following algorithms was used for comparison.

– AES-256: Used as a standard encryption solution in Python-based applications, CRYPTOGRAPHY module implementation was used in this experiment.
– OPE: Experiments carried out here use PYOPE implementation of Boldyreva et al17 symmetric OPE scheme.
– ESN: pyESN implementation of ESNs was used as base for implementing the work of Ramamurthy et al.46

Due to the $O (N^{3})$ complexity of NN-based solutions, performance of ESN-based encryption over large datasets is estimated by Monte Carlo method50 and extrapolation to dataset size provided. The ESN original paper proposes some design improvements that lower complexity to $O (N m^{2})$ , by parallelizing in blocks of size m, complexity can be lowered in big data systems. Nonetheless, they were not implemented here because achieving this implementation is system-specific and can also be applicable to other algorithms, so it was avoided in our implementation for fairness purposes.

The careful choosing of this setup aims to compare average performance of one example of each cryptographic family of schemes provided in previous sections, under similar conditions, over real-world datasets. Results from these experiments will be analyzed in the following section.

4.3 Results

Experimental results on the described conditions can be found in Figure 6. It can be seen that increasing the complexity of the algorithms also impacts performance over the different datasets. Preservation of mathematical property of order, as well as using NNs to encrypt data, have well-known advantages as already described in the document, but the trade-off between security and complexity is clear from the results.

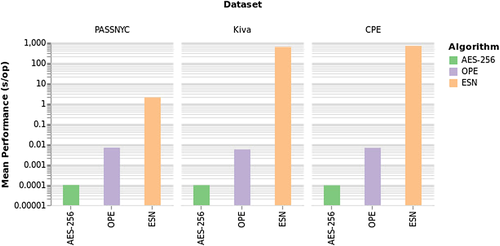
Average performance over the three datasets is stable for AES and OPE, but estimated performance over Kiva and CPE datasets of ESN is much poorer than measured for PASSNYC one. This can be derived from the estimation process already described, but also from the fact that implementation poses overhead problems that have an impact on performance. Extrapolation to big data environments can also have a severe impact in performance, and theoretical complexity can be a good bound to set expectations on encryption algorithms.

As a result, carefully choosing the right algorithm for each task in big data environment, taking into account the target application, the specific needs it entails, and how the information is required to be treated, could imply an efficiency gain of several orders and magnitude, which, in the end, results in higher system throughput and reliability.

5 CONCLUSIONS

In this document, a state-of-art review of several trends in Cryptography, which could potentially be applied in big data environments, is performed. Specific needs of big data applications, such as database processing or ML applied over encrypted data, can be achieved by the use of PPE or FHE schemes. It has been shown here that some of these schemes have unexpected information leaks to attackers mainly due to real-world variable probability distributions and variable correlations. Furthermore, efficient versions of each scheme are cited, but the need for more research effort is needed for these approaches to be widely implemented and used in commercial applications.

On the other hand, the rise of NN-based solutions for a myriad of applications also brought the attention toward the field of neural Cryptography. Intellectual efforts have proven successful for applying NNs to different tasks in cryptography, but most papers do not thrive beyond proving the concept. Nonetheless, the use of adversarial setups, well known in DL contexts, to jointly model encryption process and attackers to provide robust encryption schemes has attracted a lot of interest recently, and it is evolving at great pace. Surely, this field of neural cryptography will be empowered by a large research effort in the near future, as it is a trend that joins the rise of DL techniques with the need for security and privacy concerns to be tackled more thoroughly.

Additionally, some experiments were performed over large datasets to assess performance of different encryption algorithms and obtain some insights about extrapolating current academic work to big data environments. Design improvements can further be proposed considering tool specifics when moving toward big data setups, it is an open research question from this point of view. Moreover, considering the trade-off between security and complexity, and also jointly considering the specific needs of the individual big data application of interest, may also allow tailoring encryption schemes to optimize the trade-off.

Consequently, it has been shown that several trends in cryptography could be applied to specific needs of big data applications but at the cost of higher complexity and risks on information leakage to targeted attacks. It leads to some open research opportunities in various directions, but the promising rise of such applications is specially appealing to propose new, tailored, and flexible schemes to limit the risks posed by current state-of-art ones and improve efficiency to meet widespread demands in terms of implementation feasibility.

ACKNOWLEDGEMENT

The authors would like to thank all the people in CMMSE committee and assistants for their positive response over this research.

CONFLICT OF INTEREST

Authors declare no known relation with the corporations cited in the document or any partners, as well as no potential conflict of interest.

Biographies

Fernando Rabanal has an MSc. degree in Telecommunications Engineering from the University of Valladolid, Spain, obtained in 2011, and an MSc. degree in Multimedia and Communications from the University Carlos III of Madrid, obtained in 2013. Past research interests included Machine Learning and Human-Computer Interactions. He is now a Ph.D. candidate at the University of Oviedo in the field of Cryptography.
Consuelo Martínez is full professor of algebra at Oviedo University, Spain. She got her Ph.Degree at Zaragoza University, Spain. Her scientific interest includes algebraic structures and algebraic applications in Coding Theory and Cryptography.

REFERENCES

1Alaba FA, Othman M, Hashem IAT, Alotaibi F. Internet of Things security: a survey. J Netw Comput Appl. 2017; 88: 10-28.
10.1016/j.jnca.2017.04.002
Web of Science® Google Scholar
2Kshetri N. Big data's impact on privacy, security and consumer welfare. Telecommunications Policy. 2014; 38(11): 1134-1145.
10.1016/j.telpol.2014.10.002
Web of Science® Google Scholar
3Patil HK, Seshandri R. Big data's impact on privacy, security and consumer welfare. Paper presented at: 2014 IEEE International Congress on Big Data; 2014; Washington, DC.
Google Scholar
4Xu L, Jiang C, Wang J, Yuan J, Ren Y. Information security in big data: privacy and data mining. IEEE Access. 2014; 2: 1149-1176.
10.1109/ACCESS.2014.2362522
Web of Science® Google Scholar
5Rewagad P, Yogita P. Use of digital signature with Diffie Hellman key exchange and AES encryption algorithm to enhance data security in cloud computing. Paper presented at: 2013 International Conference on Communication Systems and Network Technologies; 2013; Gwalior, India.
Google Scholar
6Aljawarneh S, Yassein M. A multithreaded programming approach for multimedia big data: encryption system. Multimed Tools Appl. 2018; 77(9): 10997-11016.
10.1007/s11042-017-4873-9
Web of Science® Google Scholar
7Park S, Lee Y. Secure hadoop with encrypted HDFS. Paper presented at: International Conference on Green, Pervasive, and Cloud Computing; 2013; Seoul, South Korea.
Google Scholar
8Popa RA, Redfield C, Zeldovich N, Balakrishnan H. CryptDB: protecting confidentiality with encrypted query processing. In: Proceedings of the 23rd ACM Symposium on Operating Systems Principles; 2011; Cascais, Portugal.
Google Scholar
9Tu S, Kaashoek MF, Madden S, Zeldovich N. Processing analytical queries over encrypted data. Proc VLDB Endow. 2013; 6(5): 289-300.
10.14778/2535573.2488336
Google Scholar
10Kocabaş Ö, Soyata T. Medical data analytics in the cloud using homomorphic encryption. In: Handbook of Research on Cloud Infrastructures for Big Data Analytics. Hershey, PA: IGI Global; 2014: 471-488.
10.4018/978-1-4666-5864-6.ch019
Google Scholar
11Schuster F, Costa M, Fournet C, et al. VC3: trustworthy data analytics in the cloud using SGX. Paper presented at: 2015 IEEE Symposium on Security and Privacy; 2015; San Jose, CA.
Google Scholar
12Papadimitriou A, Bhagwan R, Chandran N, et al. Big data analytics over encrypted datasets with seabed. In: 12th USENIX Symposium on Operating Systems Design and Implementation; 2016; Savannah, GA.
Google Scholar
13Aljawarneh S, Yassein MB. A resource-efficient encryption algorithm for multimedia big data. Multimed Tools Appl. 2017; 76(21): 22703-22724.
10.1007/s11042-016-4333-y
Web of Science® Google Scholar
14Pandey O, Rouselakis Y. Property preserving symmetric encryption. Paper presented at: Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2012; Cambridge, UK.
Google Scholar
15Tang Q. Public key encryption supporting plaintext equality test and user-specified authorization. Secur Commun Netw. 2012; 5(12): 1351-1362.
10.1002/sec.418
Web of Science® Google Scholar
16Agrawal R, Kiernan J, Srikant R, Xu Y. Order preserving encryption for numeric data. In: Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data; 2004; Paris, France.
Google Scholar
17Boldyreva A, Chenette N, Lee Y, O'Neill A. Order-preserving symmetric encryption. Paper presented at: Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2009; Cologne, Germany.
Google Scholar
18Gentry C. Fully homomorphic encryption using ideal lattices. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing; 2009; Bethesda, MD.
Google Scholar
19Gentry C. A Fully Homomorphic Encryption Scheme. PhD thesis. Stanford, CA:Stanford University; 2009.
Google Scholar
20Chenette N, Lewi K, Weis SA, Wu SJ. Practical order-revealing encryption with limited leakage. Paper presented at: International Conference on Fast Software Encryption; 2016; Bochum, Germany.
Google Scholar
21Cash D, Liu F-H, O'Neill A, Zhang C. Reducing the leakage in practical order-revealing encryption. IACR Cryptology ePrint Archive. 2016.
Google Scholar
22Durak FB, DuBuisson TM, Cash D. What else is revealed by order-revealing encryption? In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; 2016; Vienna, Austria.
Google Scholar
23Boldyreva A, Chenette N, O'Neill A. Order-preserving encryption revisited: improved security analysis and alternative solutions. In: Advances in Cryptology – CRYPTO 2011. Berlin, Germany: Springer; 2011: 578-595.
10.1007/978-3-642-22792-9_33
Google Scholar
24Teranishi I, Yung M, Malkin T. Order-preserving encryption secure beyond one-wayness. Paper presented at: International Conference on the Theory and Application of Cryptology and Information Security; 2014; Kaoshiung, Taiwan.
Google Scholar
25Naveed M, Kamara S, Wright CV. Inference attacks on property-preserving encrypted databases. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security; 2015; Denver, CO.
Google Scholar
26Lacharité MS, Minaud B, Paterson KG. Improved reconstruction attacks on encrypted data using range query leakage. Paper presented at: 2018 IEEE Symposium on Security and Privacy (SP); 2018; San Francisco, CA.
Google Scholar
27Arasu A, Blanas S, Eguro K, et al. Orthogonal security with Cipherbase. In: Proceedings of the 6th CIDR; 2013; Pacific Grove, CA.
Google Scholar
28Naehrig M, Lauter K, Vaikuntanathan V. Can homomorphic encryption be practical? In: Proceedings of the 3rd ACM workshop on Cloud Computing Security Workshop; 2011; Chicago, IL.
Google Scholar
29Brakerski Z, Vaikuntanathan V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. Paper presented at: Annual cryptology conference; 2011; Santa Barbara, CA.
Google Scholar
30Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE. SIAM J Comput. 2014; 43(2): 831-871.
10.1137/120868669
Web of Science® Google Scholar
31Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans Comput Theory. 2014; 6(3): 13.
10.1145/2633600
Google Scholar
32Berkoff A, Liu FH. Leakage resilient fully homomorphic encryption. Paper presented at: Theory of Cryptography Conference; 2014; San Diego, CA.
Google Scholar
33Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Networks. 1989; 2(5): 359-366.
10.1016/0893-6080(89)90020-8
Web of Science® Google Scholar
34Erhan D, Bengio Y, Courville A, Manzagol PA, Vincent P, Bengio S. Why does unsupervised pre-training help deep learning? J Mach Learn Res. 2010; 11: 625-660.
Web of Science® Google Scholar
35Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy layer-wise training of deep networks. Advances in Neural Information Processing Systems. Cambridge, MA: MIT; 2007: 153-160.
Google Scholar
36Kanter I, Kinzel W, Kanter E. Secure exchange of information by synchronization of neural networks. Europhysics Letters. 2002; 57(1): 141.
10.1209/epl/i2002-00552-9
CAS Web of Science® Google Scholar
37Rosenblatt F. Principles of Neurodynamics. Perceptrons and the Theory of Brain Mechanisms. Buffalo, NY: Cornell Aeronautical Lab Inc; 1961.
10.21236/AD0256582
Google Scholar
38Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1986; 323(6088): 533-536.
10.1038/323533a0
Web of Science® Google Scholar
39De Bernardi M, Khouzani MHR, Malacaria P. Pseudo-random number generation using generative adversarial networks. Paper presented at: Joint European Conference on Machine Learning and Knowledge Discovery in Databases; 2018; Dublin, Ireland.
Google Scholar
40Zhu J, Kaplan R, Johnson J, Fei-Fei L. Hidden: hiding data with deep networks. In: Proceedings of the European Conference on Computer Vision (ECCV); 2018; Munich, Germany.
Google Scholar
41Gilad-Bachrach R, Dowlin N, Laine K, Lauter K, Naehrig M, Wernsing J. Cryptonets: applying neural networks to encrypted data with high throughput and accuracy. Paper presented at: International Conference on Machine Learning; 2016; New York, NY.
Google Scholar
42Chabanne H, de Wargny A, Milgram J, Morel C, Prouff E. Privacy-preserving classification on deep neural network. IACR Cryptology ePrint Archive 2017. 2017.
Google Scholar
43Huang C, Kairouz P, Chen X, Sankar L, Rajagopal R. Context-aware generative adversarial privacy. Entropy. 2017; 19(12): 656.
10.3390/e19120656
Web of Science® Google Scholar
44Takabi H, Hesamifard E, Ghasemi M. Privacy preserving multi-party machine learning with homomorphic encryption. Paper presented at: 29th Annual Conference on Neural Information Processing Systems (NIPS); 2016; Barcelona, Spain.
Google Scholar
45Hesamifard E, Takabi H, Ghasemi M. Cryptodl: towards deep learning over encrypted data. Paper presented at: Annual Computer Security Applications Conference (ACSAC 2016); 2016; Los Angeles, CA.
Google Scholar
46Ramamurthy R, Bauckhage C, Buza K, Wrobel S. Using echo state networks for cryptography. Paper presented at: International Conference on Artificial Neural Networks; 2017; Alghero, Italy.
Google Scholar
47Muñoz A, Escribano JI. Criptografía adversaria usando deep learning. limitaciones y oportunidades. Actas de la XV Reunión Española sobre Criptología y Seguridad de la Información. RECSI. 2018.
Google Scholar
48Papernot N. A Marauder's map of security and privacy in machine learning: an overview of current and future research directions for making machine learning secure and private. In: Proceedings of the 11th ACM Workshop on Artificial Intelligence and Security; 2018; Toronto, Canada.
Google Scholar
49Abadi M, Andersen DG. Learning to protect communications with adversarial neural cryptography. arXiv preprint arXiv:1610.06918 2016. 2016.
Google Scholar
50Metropolis N, Ulam S. The Monte Carlo method. J Am Stat Assoc. 1949; 44(247): 335-341.
10.1080/01621459.1949.10483310
CAS PubMed Web of Science® Google Scholar

2 The notion of distance in the cited work23 refers to directed modular distance, ie, the distance from one point “up” to the other point, wrapping up the space if needed (noncommutative distance).
3 All datasets cited in this document can be downloaded from https://www.kaggle.com/datasets, and used under CC0 public license. Last access:August 24, 2019.
4 All descriptions provided are summarized from dataset page.

Citing Literature

All articles

Cryptography for big data environments: Current status, challenges, and opportunities

Abstract

1 INTRODUCTION