Anomalies in the convergence of Traub-type methods with memory
Abstract
The stability analysis of a new family of iterative methods with memory is introduced. This family, designed from Traub's method, allows to add memory through the introduction of an accelerating parameter. Hence, the speed of convergence of the iterative method increases up to 3.30, with no new functional evaluations. A dynamical study of the proposed family on quadratic polynomials is presented obtaining interesting qualitative properties.
1 INTRODUCTION
Iterative methods are useful tools to approximate the solution α of a nonlinear equation f (x)=0, where
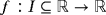 or of a nonlinear system of equations F(x)=0,
or of a nonlinear system of equations F(x)=0,
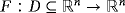 . This area of numerical analysis has experienced great growth in recent years, with the design of new iterative schemes that improve the speed of convergence and the computational efficiency of the classical methods. Possibly, advances in the computational field of mathematics have enabled this development.
. This area of numerical analysis has experienced great growth in recent years, with the design of new iterative schemes that improve the speed of convergence and the computational efficiency of the classical methods. Possibly, advances in the computational field of mathematics have enabled this development.
Given the variety of iterative schemes that exist in the literature, different classifications can be considered. The order of convergence1 gives an idea about the speed of convergence of the method to find the solution. The efficiency index, introduced by Ostrowsky2, links the order of convergence with the number of functional evaluations in each iteration. The presence or absence of derivatives in the iterative expression of the scheme restricts the problems that can be solved if these derivatives cannot be calculated. Moreover, iterative methods are classified depending if only one previous iteration is required (scheme without memory) or it is necessary to employ more than one (scheme with memory).
According to the Kung-Traub conjecture,3 iterative methods without memory with d functional evaluations per iteration have order of convergence at most 2d−1. For this reason, the order of convergence of a method can be improved by including information from several previous iterations to get the next estimation, transforming it in a method with memory. When this upper bound is reached, the scheme is called optimal. This upper bound can be avoided if we work with methods with memory. We found in the literature several researchers with important results in this area, highlighting the works of Petković,4-6 Chun and Neta,7 or Soleymani et al8, 9 among others.10-13 Most of these works are based on the inclusion of an accelerating parameter in the iterative expression of a usually known iterative scheme.
To analyze the order of convergence of an iterative method with memory, we use the following result. 14
Theorem 1.Let ψ be an iterative method with memory that generates a sequence {xk} of approximations of root α, and let this sequence converge to α. If there exist a nonzero constant η and nonnegative numbers ti, i=0,1,…,m such that the inequality
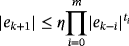
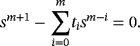
It is known14 that R-order implies the classical order of convergence and we denote by {fk}∼{gk} when sequence {fk/gk} tends to a constant when k→+∞.
In recent years, it is usual to analyze the stability of known and new iterative methods in terms of the wideness of the set of converging initial approximations when they are applied on low-degree polynomials. This analysis is usually made by using techniques from complex discrete dynamical systems. However, when memory is introduced in the iterative methods, these tools cannot be applied. Campos et al15, 16 introduced a new procedure that constructs multidimensional real dynamical systems from these schemes with memory in order to analyze their dependence on initial estimations. When there exists a dependence on a real parameter, also it is possible to select those members of the parametric family with better stability properties.
In this work, starting from a well-known third-order method without memory, we perform in Section 2 a new family of iterative methods by including parameters on the original scheme. Then, we develop step by step the inclusion of memory on the resulting scheme to enhance the original order of convergence. The result is a uniparametric family of iterative methods with memory with higher order of convergence. After we introduce some basics on real dynamics with memory in Section 3, the stability analysis of the family with memory is studied in Section 4 by using real dynamical tools on the multidimensional rational function resulting from applying the proposed class of iterative methods on low-degree polynomial. Finally, Section 5 is devoted to the main conclusions of this work.
2 DESIGNING THE FAMILY OF METHODS WITH MEMORY
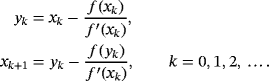 (1)
(1)In this work, method 1 is modified by including two parameters and analyzing their role in the error equation. In particular, one of these parameters will be properly fixed to generate a family of iterative methods with memory, capitalizing this role. The dynamical analysis of the iterative methods allows the knowledge of their stability in terms of dependence of initial estimations. Therefore, the resulting family with memory will be applied on arbitrary quadratic polynomials.
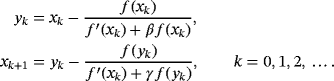 (2)
(2)The biparametric family 2 holds the original order of convergence, for all real β and γ, as shows the following result.
Theorem 2.Let
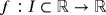 be a real differentiable function in an open interval I. If α∈I is a simple real root of f (x)=0 and x0 is close enough to α, then sequence {xk} generated by 2 converges to α with order of convergence 3 for any real value of parameters β and γ, being the error equation:
be a real differentiable function in an open interval I. If α∈I is a simple real root of f (x)=0 and x0 is close enough to α, then sequence {xk} generated by 2 converges to α with order of convergence 3 for any real value of parameters β and γ, being the error equation:
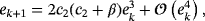 (3)
(3)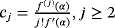 .
.
Proof.By using Taylor expansions around α, f (xk) can be written as
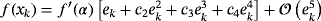
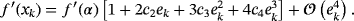
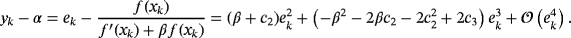
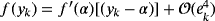 and the previous ones, the error equation of family 2 is
and the previous ones, the error equation of family 2 is
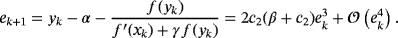
Although family 2 has third order of convergence as Traub's method, the presence of parameter β in the lower term of the error equation allows the inclusion of memory. Let us note in Equation 3 that, for β=−c2, the method reaches order 4 but c2 cannot be used as α is unknown. Therefore, an approximation of
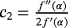 is needed to increase the order of convergence.
is needed to increase the order of convergence.
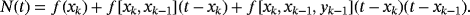 (4)
(4)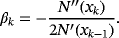 (5)
(5)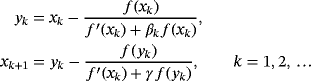 (6)
(6)The following result shows that the order of convergence of family 6, which is denoted by MMγ, results in 3.30.
Theorem 3.Let
 be a real differentiable function in an open interval I. Let α∈I be a simple real root of f (x)=0. Then, if x0 and x1 are close enough to α, the sequence generated by MMγ converges to α with order of convergence 3.30 for all value of parameter γ.
be a real differentiable function in an open interval I. Let α∈I be a simple real root of f (x)=0. Then, if x0 and x1 are close enough to α, the sequence generated by MMγ converges to α with order of convergence 3.30 for all value of parameter γ.
Proof.The error equation 3 can be written as
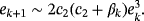 (7)
(7)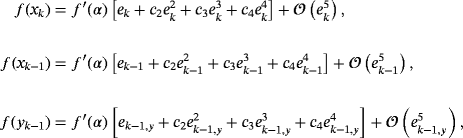
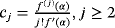 .
.From the previous developments and the definition of N(t) given by 4, the lower terms for parameter βk are
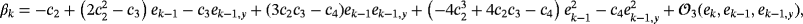
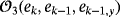 denotes all the elements that the sum of the exponents of ek, ek−1 and ek−1,y is at least 3.
denotes all the elements that the sum of the exponents of ek, ek−1 and ek−1,y is at least 3.Then, it is satisfied
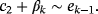 (8)
(8)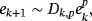
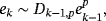 (9)
(9)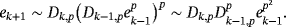 (10)
(10)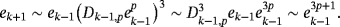 (11)
(11)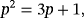
Section 3 is devoted to describe the dynamical tools that we need to analyze the dynamical behavior of family MMγ (Section 4).
3 BASICS ON REAL MULTIDIMENSIONAL DYNAMICS
The main fundamentals about dynamical analysis for iterative procedures that include memory are introduced in the following. Further information can be found in other work Campos et al15, 16 and Chicharro et al,17, 18 wherein these fundamentals are developed. Moreover, the application of these concepts on diverse schemes with memory is also performed in the aforementioned references.
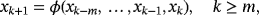
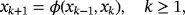
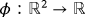 cannot have fixed points. Therefore, we define an auxiliary map
cannot have fixed points. Therefore, we define an auxiliary map
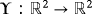 such that
such that
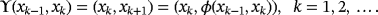
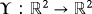 is defined as
is defined as
 (12)
(12)The orbit of a point x by Υ is defined as the set of images {x,Υ(x),Υ2(x),…,Υn(x),…}.
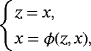
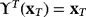 and
and
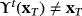 , for t<T. A T-periodic point is hyperbolic when the eigenvalues of the associated Jacobian matrix Υ′(xT) satisfy |λj|≠1, for all j. The asymptotical behavior of a periodic hyperbolic point xT is characterized in the following result.19
, for t<T. A T-periodic point is hyperbolic when the eigenvalues of the associated Jacobian matrix Υ′(xT) satisfy |λj|≠1, for all j. The asymptotical behavior of a periodic hyperbolic point xT is characterized in the following result.19
Theorem 4.Let
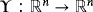 be
be
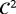 . Let us suppose xT is T-periodic. Let λ1,λ2,…,λn be the eigenvalues of
. Let us suppose xT is T-periodic. Let λ1,λ2,…,λn be the eigenvalues of
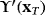 . Then,
. Then,
- xT is an attracting point when |λj|<1, ∀j;
- xT is unstable (repelling or saddle) if, at least, one eigenvalue
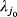 satisfies
satisfies
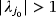 ;
; - xT is a repelling point when |λj|>1, ∀j.
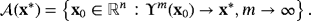
4 DYNAMICS ON MMγ
Based on the concepts introduced in Section 3, the dynamics of the family with memory MMγ when it is applied on quadratic polynomials is analyzed in this section.
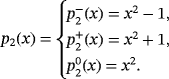
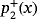 does not have real roots, the polynomial
does not have real roots, the polynomial
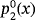 has a unique real root in x∗=0 with multiplicity 2, and the polynomial
has a unique real root in x∗=0 with multiplicity 2, and the polynomial
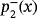 has two real roots
has two real roots
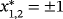 .
.4.1 Analysis of the rational functions
In order to analyze the dynamical features, family MMγ is applied on the quadratic polynomials introduced previously. The resulting rational functions are analyzed in order to find their associated fixed points and their asymptotical behavior, showing the performance of the family depending on the initial estimations.
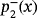 , we get the fixed-point operator
, we get the fixed-point operator
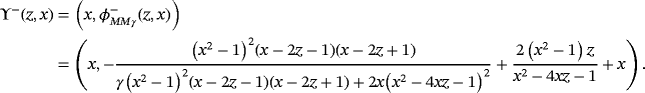 (13)
(13)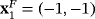 and
and
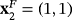 , that agree with the roots of the considered polynomial. In addition, the roots of the polynomial
, that agree with the roots of the considered polynomial. In addition, the roots of the polynomial
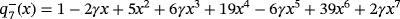
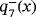 , we only consider the strange fixed points in those regions where they are real. Then, the operator has a strange fixed point for all value of γ, denoted by
, we only consider the strange fixed points in those regions where they are real. Then, the operator has a strange fixed point for all value of γ, denoted by
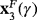 , and two strange fixed points,
, and two strange fixed points,
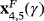 , defined only when γ∈(−∞,−γ∗)∪(γ∗,+∞), being γ∗≈3.38143 one of the roots of the polynomial
, defined only when γ∈(−∞,−γ∗)∪(γ∗,+∞), being γ∗≈3.38143 one of the roots of the polynomial
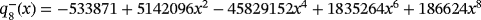 .
.Their stability depends on the value of the parameter. By analyzing the eigenvalues of the Jacobian matrix (Υ−)′(z,x) for each strange fixed point according to Theorem 4, we obtain that
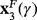 is always repelling for all real γ≠0 (see Figure 1A, where both eigenvalues are coincident and bigger than one, in absolute value),
is always repelling for all real γ≠0 (see Figure 1A, where both eigenvalues are coincident and bigger than one, in absolute value),
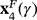 is a saddle point for γ∈(−∞,−γ∗)∪(γ∗,+∞) (it can be seen in Figure 1B that one eigenvalue is very close but lower than one and the other eigenvalue is bigger than one, in absolute value) and
is a saddle point for γ∈(−∞,−γ∗)∪(γ∗,+∞) (it can be seen in Figure 1B that one eigenvalue is very close but lower than one and the other eigenvalue is bigger than one, in absolute value) and
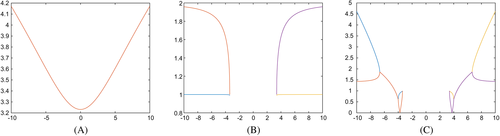
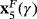 is saddle or attracting depending on the value of γ (in Figure 1C, different areas are observed where both eigenvalues are lower or bigger than one, in absolute value).
is saddle or attracting depending on the value of γ (in Figure 1C, different areas are observed where both eigenvalues are lower or bigger than one, in absolute value).
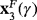 ; B,
; B,
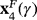 ; C,
; C,
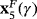
Due to the diversity of behavior of strange fixed points, these details can be summarized in Table 1 and Proposition 1.
| γ |
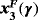 |
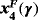 |
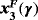 |
|---|---|---|---|
| ]−∞,−γ∗∗] | Repelling | Saddle point | Repelling |
| ]−γ∗∗,−γ∗] | Repelling | Saddle point | Attracting |
| ]−γ∗,0[ | Repelling | Not real | Not real |
| ]0,−γ∗[ | Repelling | Not real | Not real |
| [−γ∗,γ∗∗[ | Repelling | Saddle point | Attracting (γ∗≠γ∗∗) |
| ]γ∗∗,+∞[ | Repelling | Saddle point | Repelling |
Proposition 1.Rational function Υ−(z,x) has different number of fixed points,
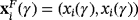 (i∈{1,2,3,4,5}), depending on the value of parameter γ. In particular,
(i∈{1,2,3,4,5}), depending on the value of parameter γ. In particular,
- (i)
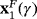 and
and
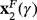 , whose components correspond to the roots of polynomial
, whose components correspond to the roots of polynomial
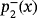 , are superattracting fixed points, with independence of the value of γ. In case of γ=0, the rational operator is simplified and points
, are superattracting fixed points, with independence of the value of γ. In case of γ=0, the rational operator is simplified and points
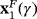 and
and
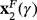 are the only fixed points of Υ−(z,x);
are the only fixed points of Υ−(z,x); - (ii)
when γ≠0, three roots of polynomial
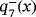 can be real:
can be real:
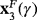 is real for any γ≠0 and it is a repelling strange fixed point;
is real for any γ≠0 and it is a repelling strange fixed point;
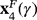 is real for γ∈]−∞,−γ∗[∪[γ∗,+∞[, being γ∗≈3.38143, and it is a saddle strange fixed point in all its domain; finally,
is real for γ∈]−∞,−γ∗[∪[γ∗,+∞[, being γ∗≈3.38143, and it is a saddle strange fixed point in all its domain; finally,
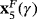 is real for γ∈]−∞,−γ∗]∪]γ∗,+∞[, and it is an attracting strange fixed point in ]−γ∗∗,−γ∗[∪]γ∗,γ∗∗[, being γ∗∗≈4.4668, and repelling in γ∈]−∞,−γ∗]∪]γ∗∗,+∞[; in the boundaries of these intervals, it is a neutral or parabolic strange fixed point.
is real for γ∈]−∞,−γ∗]∪]γ∗,+∞[, and it is an attracting strange fixed point in ]−γ∗∗,−γ∗[∪]γ∗,γ∗∗[, being γ∗∗≈4.4668, and repelling in γ∈]−∞,−γ∗]∪]γ∗∗,+∞[; in the boundaries of these intervals, it is a neutral or parabolic strange fixed point.
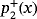 , the resulting rational operator is
, the resulting rational operator is
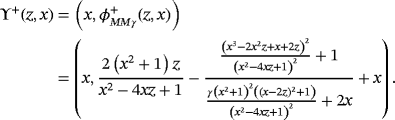 (14)
(14)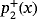 does not have real roots. In the following result, we establish the number and stability of the strange fixed points; moreover, the proof is omitted, as it is similar to that of Proposition 1.
does not have real roots. In the following result, we establish the number and stability of the strange fixed points; moreover, the proof is omitted, as it is similar to that of Proposition 1.
Proposition 2.Rational function Υ+(z,x) has different number of fixed points,
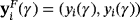 (i∈{1,2,3}), depending on the value of γ. In particular,
(i∈{1,2,3}), depending on the value of γ. In particular,
- (i) if γ=0, the rational operator is simplified and there are no strange fixed point;
- (ii)
when γ≠0, three roots of polynomial
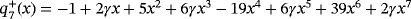 can be real:
can be real:
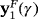 is real for any γ≠0 and it is a repelling strange fixed point;
is real for any γ≠0 and it is a repelling strange fixed point;
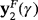 and
and
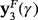 are real for γ∈]−γ♯,0[∪]0,γ♯[, being γ♯≈4.62389, being their character repelling.
are real for γ∈]−γ♯,0[∪]0,γ♯[, being γ♯≈4.62389, being their character repelling.
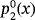 is
is
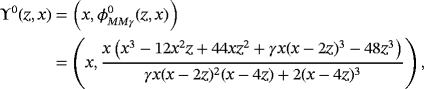 (15)
(15)
Proposition 3.Rational function Υ0(z,x) has an only attracting fixed point
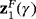 , whose components correspond to the roots of polynomial
, whose components correspond to the roots of polynomial
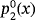 for any value of parameter γ. Moreover, it has a strange fixed point
for any value of parameter γ. Moreover, it has a strange fixed point
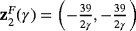 , being γ≠0, that is repelling.
, being γ≠0, that is repelling.
Then, after explaining some fundamentals about the main dynamical representations for methods with memory, the basins of attraction corresponding to the attracting fixed points of operators Υ−, Υ+, and Υ0 are depicted.
4.2 Dependence on the initial estimations
The basins of attraction of the corresponding periodic points of a method are represented in the dynamical plane. Several implementations have been made, such as in the works of Chicharro et al20 and Varona.21 However, there are some modifications in the dynamical planes when we work with two-dimensional real dynamics instead of complex dynamics. For the first case, the current iterate xk and the previous iterate xk−1 are represented as the abscissae and the ordinates, respectively. Operator Υ(z,x) is studied on a mesh of values of z and x as initial guesses that correspond to the previous and the current iterates xk−1 and xk, respectively. The basin of each attracting point is depicted with a different nonblack color. Taking a point of the mesh as an initial estimation, we paint it with the color associated to the basin of the attracting fixed point which it falls in; otherwise, the starting point is plotted in black. As described in Section 4.1, the analysis is performed over the second-degree polynomial.
The dynamical planes of some methods belonging to family MMγ when it is applied on quadratic polynomials are shown in Figures 2-6. For each operator, different values of γ have been chosen by selecting regions where the number of strange fixed points varies. Orange color denotes convergence to
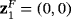 for
for
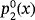 or to
or to
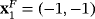 for
for
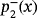 . Blue color is used to denote the convergence to
. Blue color is used to denote the convergence to
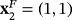 for
for
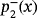 . The attracting points are represented with white stars, whereas the strange fixed points with white squares. In addition, if there is convergence to a strange fixed point, the initial guess is depicted in purple. The starting points are selected over a mesh of 500×500 points in (z,x)∈[−20,20]×[−20,20]. We set the convergence of each initial iterate to an attracting point when the difference between its successive iterates and one of the attracting points is less than 10−6 being the number of iterations lower than 50.
. The attracting points are represented with white stars, whereas the strange fixed points with white squares. In addition, if there is convergence to a strange fixed point, the initial guess is depicted in purple. The starting points are selected over a mesh of 500×500 points in (z,x)∈[−20,20]×[−20,20]. We set the convergence of each initial iterate to an attracting point when the difference between its successive iterates and one of the attracting points is less than 10−6 being the number of iterations lower than 50.
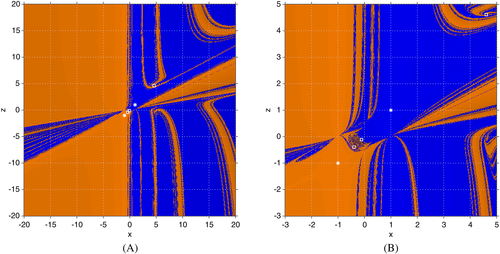
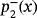 for γ=−5
for γ=−5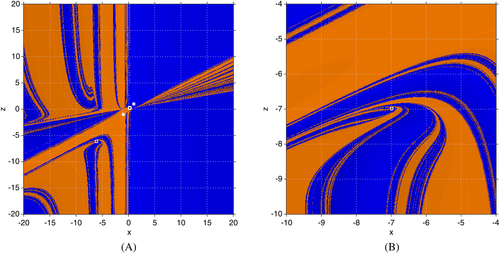
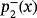 for γ=3
for γ=3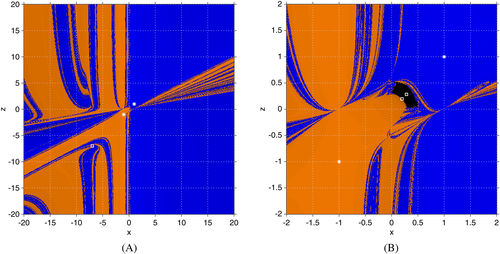
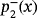 for γ=3.5
for γ=3.5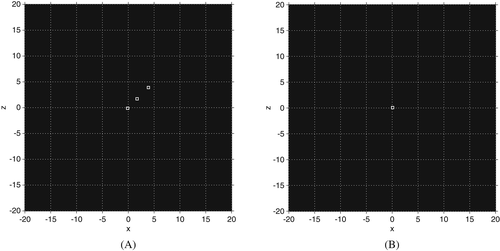
 for different values of γ. A, γ=−4; B, γ=6
for different values of γ. A, γ=−4; B, γ=6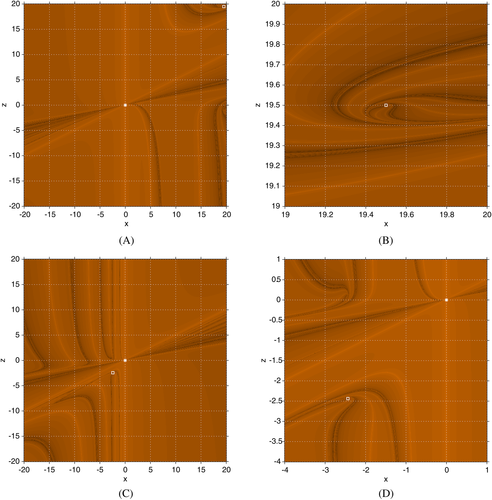
 for different values of γ. A, γ=−1; B, γ=−1, a detail; C, γ=8; D, γ=8, a detail
for different values of γ. A, γ=−1; B, γ=−1, a detail; C, γ=8; D, γ=8, a detailFigures 2-4 represents some dynamical planes of Υ−(z,x). The values for the parameter γ∈{−5,3.5,3} have been chosen. Then, for γ=−5, the associated methods of MMγ have three strange fixed points
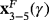 , and for γ=3, there is only one strange fixed point,
, and for γ=3, there is only one strange fixed point,
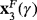 . As we can see, in these cases, there is full convergence to
. As we can see, in these cases, there is full convergence to
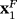 or
or
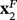 . This is the expected behavior for Figures 2 and 3 as the strange fixed points are repelling or saddle (and there are no attracting periodic orbit). The strange fixed points are represented with white squares and laid in the Julia set, as it is expected.
. This is the expected behavior for Figures 2 and 3 as the strange fixed points are repelling or saddle (and there are no attracting periodic orbit). The strange fixed points are represented with white squares and laid in the Julia set, as it is expected.
The dynamical planes of family MMγ on
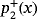 for the values of the parameter considered are shown in Figure 5. For γ=−4, methods have two repelling strange fixed points
for the values of the parameter considered are shown in Figure 5. For γ=−4, methods have two repelling strange fixed points
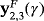 . Moreover, in the second case,
. Moreover, in the second case,
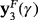 is a saddle point. It is observed that the dynamical planes are always completely black since the initial estimations do not reach to any real zero. This result agrees with the previous analysis, where it has been obtained that the only fixed points of the rational operator Υ+ where strange fixed points and they were not attracting in any case.
is a saddle point. It is observed that the dynamical planes are always completely black since the initial estimations do not reach to any real zero. This result agrees with the previous analysis, where it has been obtained that the only fixed points of the rational operator Υ+ where strange fixed points and they were not attracting in any case.
The application of MMγ on
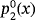 results in a dynamical plane whose behavior is the expected one since the strange point
results in a dynamical plane whose behavior is the expected one since the strange point
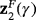 is always repelling and lay in the Julia set; in Figure 6, all the starting approximations in the Fatou set tend to the unique zero of the polynomial.
is always repelling and lay in the Julia set; in Figure 6, all the starting approximations in the Fatou set tend to the unique zero of the polynomial.
5 CONCLUSIONS
A new family of iterative methods with memory have been constructed starting from the classical Traub's method of third order of convergence. The proposed family has performed the inclusion of memory by including parameters in the iterative expression. The proper replacement of an accelerating parameter by using the expression of the error equation and the Newton's interpolation polynomial of second order has given a uniparametric family with order of convergence 3.30. Regarding the original iterative method, the value of the order of convergence has increased.
The study of the stability has been performed by means of dynamical analysis. Since the iterative scheme include memory, the complex dynamics has been replaced by the multidimensional real dynamics. Quadratic polynomials have been used as nonlinear functions for the analysis of the method. The choice of the polynomials is based on the different number of roots. For each particular case, we have chosen a particular value of the parameter to represent the basins of attraction of the associated method of the family.
In all cases, the stability has shown a good performance, as it is represented in the dynamical planes. In particular, for the polynomials that have real roots, every initial guess not only converges but also tends its orbit to the real root, showing that family MMγ behaves properly.
ACKNOWLEDGEMENTS
This research was partially supported by the Ministerio de Ciencia, Innovación y Universidades (Spain) (PGC2018-095896-B-C22) and Generalitat Valenciana (PROMETEO/2016/089). In addition, the authors would like to thank the anonymous reviewers for their suggestions and comments that have improved the final version of this manuscript.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
Biographies

Francisco I. Chicharro received the PhD in Mathematics in 2017 and the PhD in Telecommunications in 2018, both at the Universitat Politècnica de València. He is an assistant professor at the Universidad Internacional de La Rioja (UNIR). He is an author of more than ten research papers covering the areas of mathematical computation and optical transmission of OFDM signals.

Alicia Cordero received the PhD in Mathematics in 2003 at the Universitat Jaume I. She is a full professor of Mathematics at the Universitat Politècnica de València. She is an author of more than one hundred research papers. Her current research focuses on dynamical systems and numerical analysis, highlighting the iterative methods for solving nonlinear equations and systems, as well as the dynamical study of the rational functions involved in these processes.

Neus Garrido obtained the Master of Mathematics in 2017 at the Universitat Politècnica de València. She serves as a researcher for the Department of Mathematics at the Universitat Politècnica de València. She is carrying out with the PhD studies in Mathematics. Her research lines are iterative methods for solving nonlinear equations and systems.

Juan R. Torregrosa received the PhD in Mathematics in 1990 at the Universitat de València. He is a full professor of Mathematics at Universitat Politècnica de València. He has published more than 200 research papers. His current research is devoted to numerical analysis. He focuses on different problems about the solution of nonlinear equations and systems, matrix equations, and dynamical analysis of rational functions involving the iterative methods.




