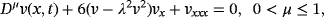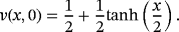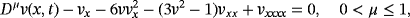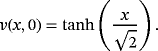Two novel computational techniques for fractional Gardner and Cahn-Hilliard equations
Abstract
The numerical solutions for nonlinear fractional Gardner and Cahn-Hilliard equations arising in fluids flow are obtained with the aid of two novel techniques, namely, fractional natural decomposition method (FNDM) and q-homotopy analysis transform method (q-HATM). Both featured techniques are different from each other since FNDM is algorithmic by the aid of Adomian polynomial and q-HATM is defined by the help of homotopy polynomial. The numerical simulations have been conducted to verify that the proposed schemes are reliable and accurate. The outcomes are revealed through the plots and tables. The comparison of solution obtained by proposed schemes with the available solutions exhibits that both the featured schemes are methodical, efficient, and very exact in solving the nonlinear complex phenomena.
1 INTRODUCTION
Integration and differentiation with noninteger order is called as fractional calculus (FC), which is the general expansion of the integer-order calculus to arbitrary order. The history of FC is traced back to 1695, while l'Hopital wrote a letter to Leibniz about the possible meaning of
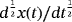 , which symbolize the semiderivative of x(t) with respect to t. Recently, FC becomes a powerful tool due to its favorable properties such as analyticity, linearity, and nonlocality. Moreover, many pioneering references are available for diverse definitions of FC, which laid the groundwork for FC.1-6 With the swift growth of digital computer knowledge, many researchers begin to work on the theory and applications of the FC. The theory of fractional-order calculus has been related to practical projects and it has been applied to chaos theory,7 signal processing,8 noisy environment,9 optics,10 and other areas.11-17 The analytical and numerical solutions for differential equations of arbitrary order arose in the above phenomena play a vital role in describing the characters of nonlinear problems exist in daily life.
, which symbolize the semiderivative of x(t) with respect to t. Recently, FC becomes a powerful tool due to its favorable properties such as analyticity, linearity, and nonlocality. Moreover, many pioneering references are available for diverse definitions of FC, which laid the groundwork for FC.1-6 With the swift growth of digital computer knowledge, many researchers begin to work on the theory and applications of the FC. The theory of fractional-order calculus has been related to practical projects and it has been applied to chaos theory,7 signal processing,8 noisy environment,9 optics,10 and other areas.11-17 The analytical and numerical solutions for differential equations of arbitrary order arose in the above phenomena play a vital role in describing the characters of nonlinear problems exist in daily life.
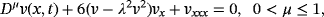 (1)
(1)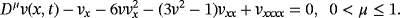 (2)
(2)The lost thirty years have been the witness for the development of a number of new and advanced schemes to study the nonlinear differential system having fractional order, and in parallel to the formation of new computational algorithms and symbolic programming. Most of the complex phenomena including chaos, solitons, asymptotic properties, and singular formation are remained undetected or at feebly projected in the precomputer era. New mathematical theories and analytical techniques are combined with recent computational algorithms that have precipitated this revolution in our understanding and aid us to study the nonlinear complex phenomena.
The analytical and numerical solutions for the nonlinear fractional differential equations have fundamental importance.27-33 Since most of the complex phenomena are modeled mathematically by nonlinear fractional differential equations, there are many methods in the literature to solve these equations. The Gardner and Cahn-Hilliard equations are studied through distinct techniques such as reduced differential transform method,34 the modified Kudryashov technique,35 Adomian decomposition method (ADM),36 improved (G′/G) − expansion method,37 homotopy perturbation method (HPM),26 residual power series method (RPSM),22 and many others.38, 39 In this framework, we employ two distinct and efficient techniques, ie, fractional natural decomposition method (FNDM) and q-homotopy analysis transform methodq-HATM, to find the solution for both cited equations.
2 PRELIMINARIES
We recall the definitions and notations of FC and Laplace transform (LT), which shall be employed in this framework
Definition 1.The fractional integral of a function f (t) ∈ Cδ(δ ≥ −1) and of order μ > 0, initially defined by Riemann-Liouville, which is presented1, 2 as
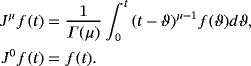 (3)
(3)Definition 2.The fractional derivative of
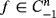 in the Caputo3 sense is defined as
in the Caputo3 sense is defined as
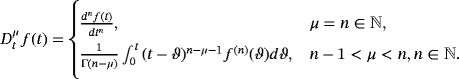 (4)
(4)Definition 3.The LT of a Caputo fractional derivative
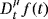 is represented4, 5 as
is represented4, 5 as
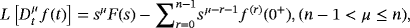 (5)
(5)Definition 4.The Mittag-Leffler type of one-parameter function is defined by the series expansion40
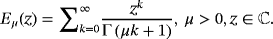 (6)
(6)Definition 5.The natural transform (NT) of the function f (t) is denoted by ℕ[ f (t)] for t ∈ ℝ and defined41 by
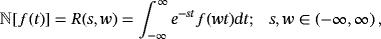
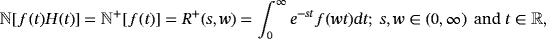 (7)
(7)
Theorem 1. (See the work of Rawashdeh[42])Let R (s, w) be the NT of the function f (t), then the NT Rμ(s, w) of the Riemann-Liouville fractional derivative of f (t) is symbolize by Dμ f (t), and which is presented as
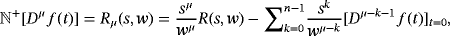 (8)
(8)Theorem 2. (See the work of Rawashdeh[42])Let R (s, w) be the NT of the function f (t), then the NT Rμ(s, w) of the Caputo fractional derivative of f (t) is symbolize by cDμ f (t), and which is presented as
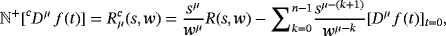 (9)
(9)3 FUNDAMENTAL IDEA OF FNDM AND q-HATM
Case (i): Fractional Natural Decomposition Method
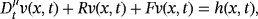 (10)
(10)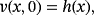 (11)
(11)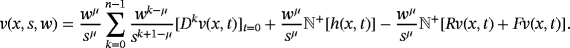 (12)
(12)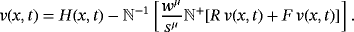 (13)
(13)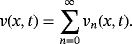 (14)
(14)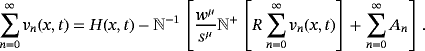 (15)
(15)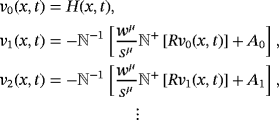
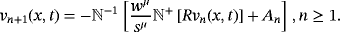 (16)
(16)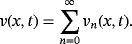
In 1992, Liao proposed homotopy analysis method (HAM)47, 48 by employing the fundamental concept of differential geometry and topology, called homotopy. The HAM has been effectively aided to find the solution for problems arises in connected areas of science and technology. Furthermore, q-HATM was proposed by Singh et al,49 which is an elegant amalgamation of q-HAM and LT. Recently, many authors study the different phenomena situated in different areas with the help of q-HATM, such as Srivastava et al studied the model of vibration equation of arbitrary order,50 Singh et al are employed to find the solution for advection-dispersion equation,51 Bulut et al analyze HIV infection of CD4+T lymphocyte cells of fractional model,52 Veeresha et al find the solution for fractional KdV-Burgers equation,53 Kumar et al analyze the model of Lienard's equation,54 and many others.55-58
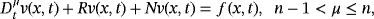 (17)
(17)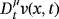 denotes the Caputo's fractional derivative of the function v (x, t), R is the bounded linear differential operator in x and t, (ie, for a number ε > 0, we have ‖Rv‖ ≤ ε‖v‖), N specifies the nonlinear differential operator and Lipschitz continuous with σ > 0 satisfying |Nv − Nw| ≤ σ|v − w|, and f (x, t) represents the source term.
denotes the Caputo's fractional derivative of the function v (x, t), R is the bounded linear differential operator in x and t, (ie, for a number ε > 0, we have ‖Rv‖ ≤ ε‖v‖), N specifies the nonlinear differential operator and Lipschitz continuous with σ > 0 satisfying |Nv − Nw| ≤ σ|v − w|, and f (x, t) represents the source term.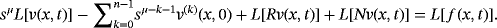 (18)
(18)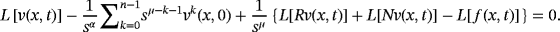 (19)
(19)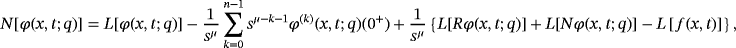 (20)
(20)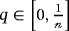 , and φ(x, t; q) is real function of x, t, and q. For nonzero auxiliary function, we construct a homotopy as follows:
, and φ(x, t; q) is real function of x, t, and q. For nonzero auxiliary function, we construct a homotopy as follows:
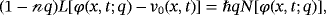 (21)
(21)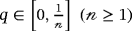 is the embedding parameter, ℏ ≠ 0 is an auxiliary parameter, φ(x, t; q) is an unknown function, and v0(x, t) is an initial guess of v(x, t). The following results hold, respectively, for q = 0 and
is the embedding parameter, ℏ ≠ 0 is an auxiliary parameter, φ(x, t; q) is an unknown function, and v0(x, t) is an initial guess of v(x, t). The following results hold, respectively, for q = 0 and
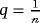 ;
;
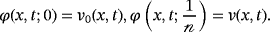 (22)
(22)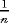 , the solution φ(x, t; q) converges from v0(x, t) to the solution v(x, t). Expanding the function φ(x, t; q) in series form by employing Taylor theorem59 near to q, one can get
, the solution φ(x, t; q) converges from v0(x, t) to the solution v(x, t). Expanding the function φ(x, t; q) in series form by employing Taylor theorem59 near to q, one can get
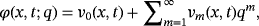 (23)
(23)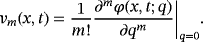 (24)
(24)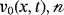 , and ℏ, the series 23 converges at
, and ℏ, the series 23 converges at
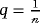 and then it yields one of the solutions for Equation 17
and then it yields one of the solutions for Equation 17
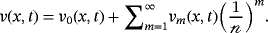 (25)
(25)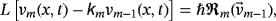 (26)
(26)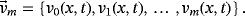 (27)
(27)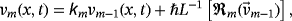 (28)
(28)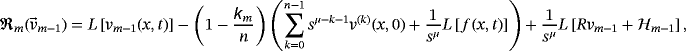 (29)
(29)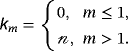 (30)
(30)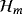 denotes homotopy polynomial and defined as
denotes homotopy polynomial and defined as
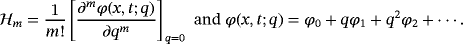 (31)
(31)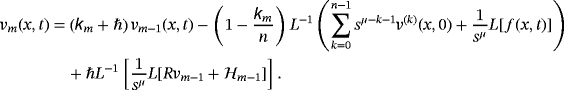 (32)
(32)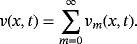 (33)
(33)4 SOLUTION FOR TIME-FRACTIONAL GARDNER EQUATIONS
In this part, we consider two examples to validate the applicability and efficiency of the proposed algorithms.
Case (i): FNDM for FG equation
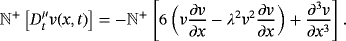 (36)
(36)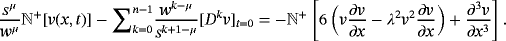 (37)
(37)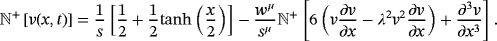 (38)
(38)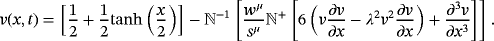 (39)
(39)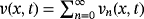 . Note that,
. Note that,
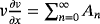 and
and
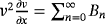 are the Adomian polynomial, which signify the nonlinear term. Now, we rewrite Equation 39 as
are the Adomian polynomial, which signify the nonlinear term. Now, we rewrite Equation 39 as
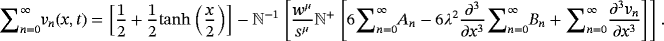 (40)
(40)
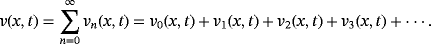
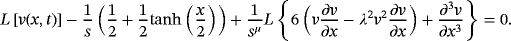 (41)
(41)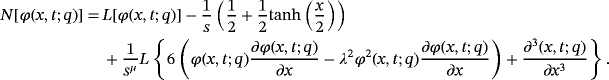 (42)
(42)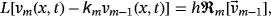 (43)
(43)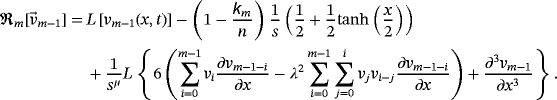 (44)
(44)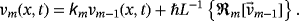 (45)
(45)
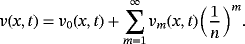 (46)
(46)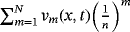 converges to the exact solution
converges to the exact solution
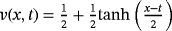 of the classical-order Gardner equation as N → ∞.
of the classical-order Gardner equation as N → ∞.
Case (i): FNDM for FCH equation
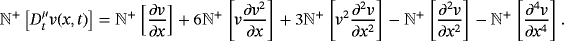 (49)
(49)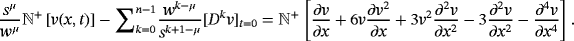 (50)
(50)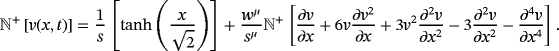 (51)
(51)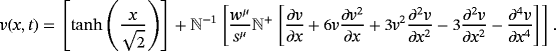 (52)
(52)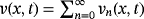 . Note that,
. Note that,
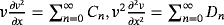 is the Adomian polynomial, which signifies the nonlinear term. Then, we can rewrite Equation 52 as
is the Adomian polynomial, which signifies the nonlinear term. Then, we can rewrite Equation 52 as
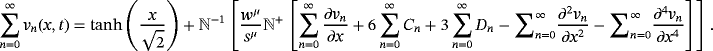 (53)
(53)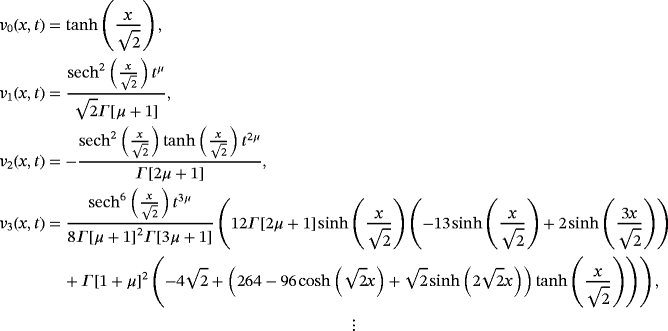
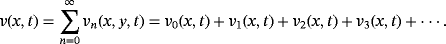
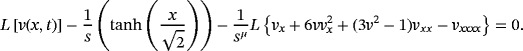 (54)
(54)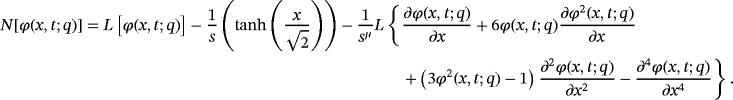 (55)
(55)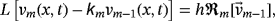 (56)
(56)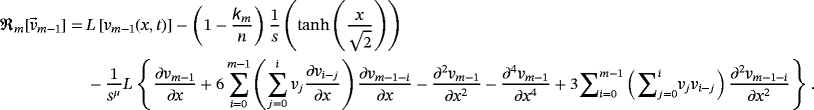 (57)
(57)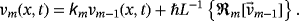 (58)
(58)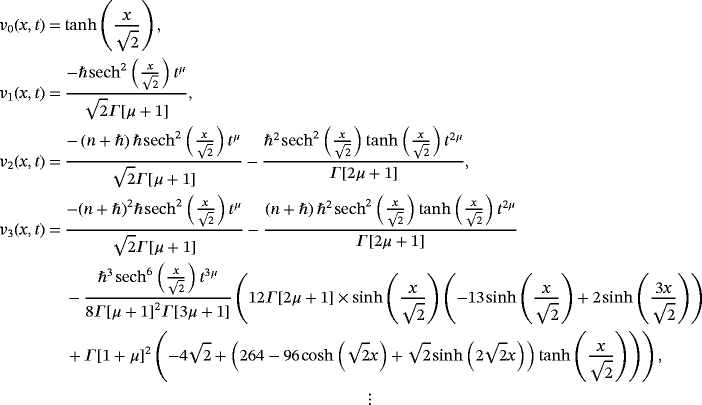
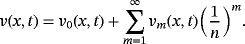 (59)
(59)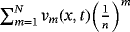 converges to the exact solution
converges to the exact solution
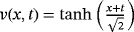 of the classical-order Cahn-Hilliard equation as N → ∞.
of the classical-order Cahn-Hilliard equation as N → ∞.5 NUMERICAL RESULTS AND DISCUSSION
In this segment, we conducted the numerical simulation for fractional-order Gardner and Cahn-Hilliard equations obtained with FNDM and q-HATM. In Table 1, we present the comparative study of the obtained solution for FG equation with RPS, q-HAM, FNDM, and q-HATM in terms of absolute error and which reveals that the proposed sachems are highly accurate in comparison with RPS and q-HAM. Furthermore, the error analysis has been conducted for the obtained solution with the help of q-HATM, which is cited in Table 2. Similarly, the Table 3 exhibits the comparison of solution for FCH equation obtained with the aid of RPS, HPM, FNDM, and q-HATM, which is studied in Example 2 and moreover, the error analysis for the obtained solution with the aid of q-HATM for the corresponding equation is presented in Table 4. The considered algorithms are very effective and accurate as compared to RPS and HPM where solving the FCH equation is shown in Table 3. From the cited tables, we can say that the projected schemes are highly accurate and moreover, as value of μ increases from μ = 0.6 to 1, the solution gets closer to the exact solution.
| x | RPS | q-HAM | FNDM | q-HATM |
|---|---|---|---|---|
| 0.1 | 1.66002 × 10−4 | 1.66002 × 10−4 | 9.95627 × 10−7 | 9.95627 × 10−7 |
| 0.2 | 1.62707 × 10−4 | 1.62707 × 10−4 | 2.61331 × 10−6 | 2.61331 × 10−6 |
| 0.3 | 1.56257 × 10−4 | 1.56257 × 10−4 | 4.12217 × 10−6 | 4.12217 × 10−6 |
| 0.4 | 1.46917 × 10−4 | 1.46917 × 10−4 | 5.46303 × 10−6 | 5.46303 × 10−6 |
| 0.5 | 1.35064 × 10−4 | 1.35064 × 10−4 | 6.58827 × 10−6 | 6.58827 × 10−6 |
- Abbreviations: FG, fractional Gardner; FNDM, fractional natural decomposition method; q-HAM, q-homotopy analysis method; q-HATM, q-homotopy analysis transform method; RPS, residual power series.
| x | t | μ = 0.60 | μ = 0.75 | μ = 0.90 | μ = 1 |
|---|---|---|---|---|---|
| 0.2 | 5.34035 × 10−2 | 2.86199 × 10−2 | 9.81980 × 10−3 | 8.34333 × 10−6 | |
| 0.4 | 6.47134 × 10−2 | 3.76411 × 10−2 | 1.39023 × 10−2 | 1.34315 × 10−4 | |
| 1 | 0.6 | 6.52772 × 10−2 | 4.06362 × 10−2 | 1.61462 × 10−2 | 6.78915 × 10−4 |
| 0.8 | 5.92624 × 10−2 | 3.98561 × 10−2 | 1.75425 × 10−2 | 2.12499 × 10−3 | |
| 1 | 4.89233 × 10−2 | 3.67019 × 10−2 | 1.89179 × 10−2 | 5.09463 × 10−3 | |
| 0.2 | 3.32479 × 10−2 | 1.71649 × 10−2 | 5.73268 × 10−3 | 1.62645 × 10−6 | |
| 0.4 | 4.54214 × 10−2 | 2.51691 × 10−2 | 8.91057 × 10−3 | 3.01592 × 10−5 | |
| 2 | 0.6 | 5.17971 × 10−2 | 3.03883 × 10−2 | 1.13275 × 10−2 | 1.74872 × 10−4 |
| 0.8 | 5.37678 × 10−2 | 3.34492 × 10−2 | 1.32775 × 10−2 | 6.25916 × 10−4 | |
| 1 | 5.18980 × 10−2 | 3.46407 × 10−2 | 1.50278 × 10−2 | 1.71161 × 10−3 | |
| 0.2 | 1.56221 × 10−2 | 7.85701 × 10−3 | 2.57966 × 10−3 | 1.23118 × 10−6 | |
| 0.4 | 2.29258 × 10−2 | 1.22352 × 10−2 | 4.19626 × 10−3 | 1.92925 × 10−5 | |
| 3 | 0.6 | 2.80066 × 10−2 | 1.56509 × 10−2 | 5.51982 × 10−3 | 9.48253 × 10−5 |
| 0.8 | 3.10943 × 10−2 | 1.81258 × 10−2 | 6.51345 × 10−3 | 2.87866 × 10−4 | |
| 1 | 3.20344 × 10−2 | 1.94719 × 10−2 | 7.05633 × 10−3 | 6.66089 × 10−4 | |
| 0.2 | 6.35626 × 10−3 | 3.15624 × 10−3 | 1.02791 × 10−3 | 9.18507 × 10−7 | |
| 0.4 | 9.63214 × 10−3 | 5.04774 × 10−3 | 1.70447 × 10−3 | 1.50782 × 10−5 | |
| 4 | 0.6 | 1.21161 × 10−2 | 6.61761 × 10−3 | 2.27076 × 10−3 | 7.82389 × 10−5 |
| 0.8 | 1.38157 × 10−2 | 7.81892 × 10−3 | 2.67148 × 10−3 | 2.53112 × 10−4 | |
| 1 | 1.45701 × 10−2 | 8.49637 × 10−3 | 2.79119 × 10−3 | 6.31476 × 10−4 | |
| 0.2 | 2.43086 × 10−3 | 1.20075 × 10−3 | 3.89768 × 10−4 | 4.17037 × 10−7 | |
| 0.4 | 3.73067 × 10−3 | 1.94069 × 10−3 | 6.51151 × 10−4 | 6.91883 × 10−6 | |
| 5 | 0.6 | 4.74585 × 10−3 | 2.56862 × 10−3 | 8.71563 × 10−4 | 3.63343 × 10−5 |
| 0.8 | 5.46580 × 10−3 | 3.05772 × 10−3 | 1.02320 × 10−3 | 1.19162 × 10−4 | |
| 1 | 5.81250 × 10−3 | 3.33519 × 10−3 | 1.05026 × 10−3 | 3.01956 × 10−4 |
| x | RPS | HPM | FNDM | q-HATM |
|---|---|---|---|---|
| 0.1 | 2.55541 × 10−5 | 2.55541 × 10−5 | 7.55258 × 10−6 | 7.55258 × 10−6 |
| 0.2 | 4.15291 × 10−5 | 4.15291 × 10−5 | 1.27010 × 10−5 | 1.27010 × 10−5 |
| 0.3 | 5.42246 × 10−5 | 5.42246 × 10−5 | 1.68403 × 10−5 | 1.68403 × 10−5 |
| 0.4 | 6.28898 × 10−5 | 6.28898 × 10−5 | 1.97175 × 10−5 | 1.97175 × 10−5 |
| 0.5 | 6.72637 × 10−5 | 6.72637 × 10−5 | 2.12349 × 10−5 | 2.12349 × 10−5 |
- Abbreviations: FCH, fractional Cahn-Hilliard; FNDM, fractional natural decomposition method; HPM, homotopy perturbation method; q-HATM, q-homotopy analysis transform method; RPS, residual power series.
| x | t | μ = 0.60 | μ = 0.75 | μ = 0.90 | μ = 1 |
|---|---|---|---|---|---|
| 0.2 | 3.58178 × 10−2 | 1.61270 × 10−2 | 4.66145 × 10−3 | 4.50019 × 10−9 | |
| 0.4 | 4.80657 × 10−2 | 2.35822 × 10−2 | 7.35085 × 10−3 | 7.14309 × 10−8 | |
| 1 | 0.6 | 5.55786 × 10−2 | 2.86384 × 10−2 | 9.34176 × 10−3 | 3.58715 × 10−7 |
| 0.8 | 6.06108 × 10−2 | 3.22934 × 10−2 | 1.08857 × 10−2 | 1.12452 × 10−6 | |
| 1 | 6.40816 × 10−2 | 3.49898 × 10−2 | 1.21017 × 10−2 | 2.72292 × 10−6 | |
| 0.2 | 1.14677 × 10−2 | 5.28714 × 10−3 | 1.54270 × 10−3 | 9.21831 × 10−10 | |
| 0.4 | 1.48415 × 10−2 | 7.58650 × 10−3 | 2.40425 × 10−3 | 1.48086 × 10−8 | |
| 2 | 0.6 | 1.65156 × 10−2 | 9.03364 × 10−3 | 3.01844 × 10−3 | 7.52569 × 10−8 |
| 0.8 | 1.72692 × 10−2 | 9.97415 × 10−3 | 3.47280 × 10−3 | 2.38723 × 10−7 | |
| 1 | 1.74227 × 10−2 | 1.05622 × 10−2 | 3.80936 × 10−3 | 5.84864 × 10−7 | |
| 0.2 | 3.02520 × 10−3 | 1.39445 × 10−3 | 4.07512 × 10−4 | 5.99891 × 10−10 | |
| 0.4 | 3.93046 × 10−3 | 1.99655 × 10−3 | 6.33354 × 10−4 | 9.55773 × 10−9 | |
| 3 | 0.6 | 4.41107 × 10−3 | 2.37627 × 10−3 | 7.93384 × 10−4 | 4.81816 × 10−8 |
| 0.8 | 4.67260 × 10−3 | 2.62688 × 10−3 | 9.11323 × 10−4 | 1.51634 × 10−7 | |
| 1 | 4.79913 × 10−3 | 2.79033 × 10−3 | 9.98715 × 10−4 | 3.68635 × 10−7 | |
| 0.2 | 7.51642 × 10−4 | 3.46050 × 10−4 | 1.01150 × 10−4 | 1.75152 × 10−10 | |
| 0.4 | 9.79798 × 10−4 | 4.95461 × 10−4 | 1.57115 × 10−4 | 2.78759 × 10−9 | |
| 4 | 0.6 | 1.10541 × 10−3 | 5.90122 × 10−4 | 1.96743 × 10−4 | 1.40376 × 10−8 |
| 0.8 | 1.17939 × 10−3 | 6.53342 × 10−4 | 2.25972 × 10−4 | 4.41323 × 10−8 | |
| 1 | 1.22250 × 10−3 | 6.95631 × 10−4 | 2.47702 × 10−4 | 1.07179 × 10−7 | |
| 0.2 | 1.83731 × 10−4 | 8.45558 × 10−5 | 2.47164 × 10−5 | 4.44363 × 10−11 | |
| 0.4 | 2.39737 × 10−4 | 1.21068 × 10−4 | 3.83865 × 10−5 | 7.07046 × 10−10 | |
| 5 | 0.6 | 2.70883 × 10−4 | 1.44234 × 10−4 | 4.80652 × 10−5 | 3.55968 × 10−9 |
| 0.8 | 2.89599 × 10−4 | 1.59760 × 10−4 | 5.52062 × 10−5 | 1.11885 × 10−8 | |
| 1 | 3.00949 × 10−4 | 1.70218 × 10−4 | 6.05207 × 10−5 | 2.71662 × 10−8 |
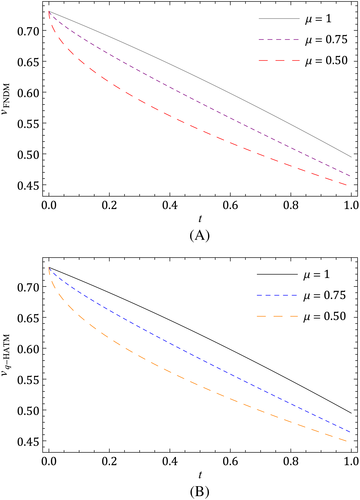
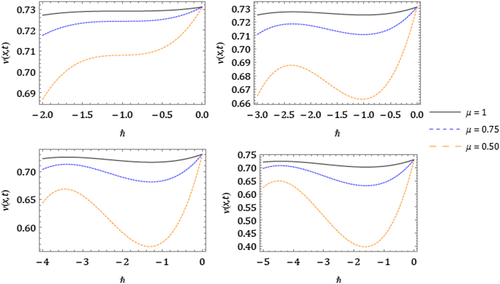
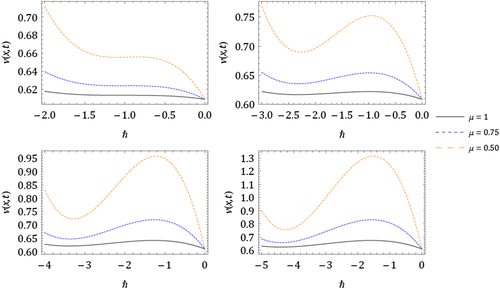
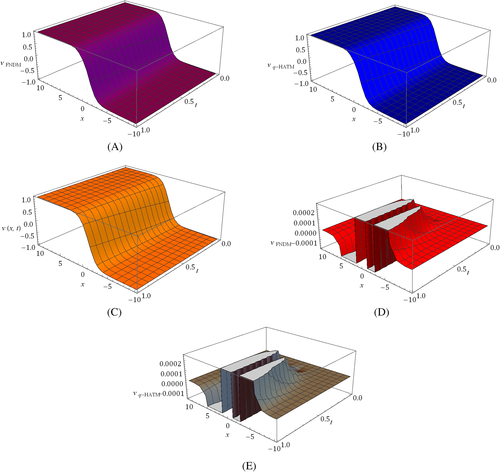
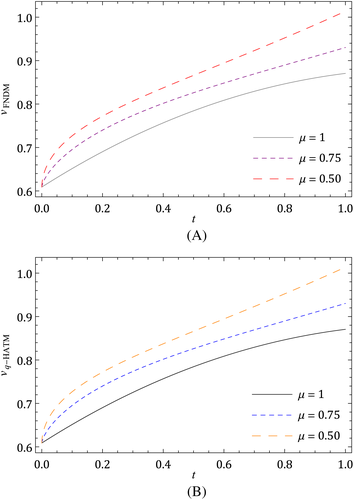
The nature of the solution v(x, t) obtained by FNDM and q-HATM for Example 1 are, respectively, presented in Figures 1A and 1B. The surface of the exact solution for Equation 33 is illustrated in Figure 1C and the behavior of absolute error for corresponding equation obtained both techniques is plotted in Figures 1D and 1E. Figures 2A and 2B are the response of the obtained solution by the two cases of Example 1 with distinct fractional Brownian motion and standard motion (μ = 1). We can see that, as time increases, the solution of FG equation decreases. Figures 3 and 4 represent the ℏ-curves with diverse values of μ and n obtained by q-HATM, respectively, for FG and FCH equations, which help us to control and adjust the convergence region of the series solution. In the similar manner, we plotted the surfaces of FNDM and q-HATM solutions, exact solution, and absolute error for the FCH equation in Figures 5A and 5E. The behavior of solution obtained by the cases (i) and (ii) studied in Example 2 with diverse values μ are presented, respectively, in Figures 6A and 6B. From the plots, we can say that, as time increases, the solution of FCH equation also increases.
6 CONCLUSION
In this investigation, we profitably employed two numerical techniques called FNDM and q-HATM to find the solution for Cahn-Hilliard and Gardner equations of arbitrary order. The novelty of the proposed techniques is that they provide nonlocal effect, straightforward solution procedure, promising large convergence region, moreover, free from any assumption, discretization, and perturbation. From the obtained results and numerical simulation, we can see that the considered methods are highly accurate as compared to HPM, q-HAM, and RPSM. The outcomes expose that the results achieved with the aid of q-HATM are more general and contain the results of RPSM, HPM, q-HAM, and FNDM as particular case. The q-HATM algorithm controls and manipulates the series solution, which quickly converges to the exact solution in a short permissible region. Finally, we can conclude that both the proposed algorithms are highly methodical and more accurate, which can be used to study nonlinear problems arisen in complex phenomena.
ACKNOWLEDGEMENT
All authors would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.
Biographies

D. G. Prakasha is a faculty member in the Department of Mathematics, Karnatak University, Dharwad, India. His areas of research interests are differential geometry of manifolds, applied mathematics, fractional calculus, numerical analysis, and theory of relativity. He published more than 70 research papers in national and international journal of repute.

P. Veeresha is a research scholar in the Department of Mathematics, Karnatak University. He received his MSc degree (2014) from Davangere University, Shivagangotri, Davangere, India. His areas of research interests are applied mathematics, fractional calculus, numerical analysis, and differential geometry of manifolds.

Haci Mehmet Baskonus is currently an associate professor in Department of Mathematics and Science Education, Faculty of Education, Harran University, Sanliurfa, Turkey. He has published more than 115 articles in various reputed and leading journals being SCI, SCI-E, E-SCI, and many others. His research interests include ordinary and partial differential equations, analytical methods for linear and nonlinear differential equations, mathematical physics, numerical solutions of the partial differential equations, fractional differential equations (of course ordinary and partial), and computer programmings such as mathematica, Pascal, and Maple.