Canadian Journal of Statistics
Early View e70012
Research Article
Open Access

Restricted Tweedie stochastic block models

Jie Jian, 

Corresponding Author

Jie Jian

Data Science Institute, The University of Chicago, Chicago, Illinois, USA

Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Canada

Corresponding author [email protected]

Search for more papers by this author
Mu Zhu, 

Mu Zhu

Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Canada

Search for more papers by this author
Peijun Sang, 

Peijun Sang

Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Canada

Search for more papers by this author
First published: 23 June 2025
https://doi.org/10.1002/cjs.70012

Abstract

en

The stochastic block model (SBM) is a widely used framework for community detection in networks, where the network structure is typically represented by an adjacency matrix. However, conventional SBMs are not directly applicable to an adjacency matrix that consists of nonnegative zero-inflated continuous edge weights. To model the international trading network, where edge weights represent trading values between countries, we propose an SBM based on a restricted Tweedie distribution. Additionally, we incorporate nodal information, such as the geographical distance between countries, and account for its dynamic effect on edge weights. Notably, we show that given a sufficiently large number of nodes, estimating this covariate effect becomes independent of community labels of each node when computing the maximum likelihood estimator of parameters in our model. This result enables the development of an efficient two-step algorithm that separates the estimation of covariate effects from other parameters. We demonstrate the effectiveness of our proposed method through extensive simulation studies and an application to international trading data.

Résumé

fr

Le modèle à blocs stochastiques (SBM) constitue un cadre de référence largement utilisé pour la détection de communautés au sein des réseaux, dans lesquels la structure est généralement représentée par une matrice d'adjacence. Cependant, les SBM classiques ne sont pas directement adaptés à une matrice d'adjacence comportant des poids d'arêtes continus, non négatifs et sujets à une inflation en zéros. Afin de modéliser le réseau commercial international, où les poids des arêtes correspondent aux valeurs des échanges entre pays, les auteurs proposent un SBM fondé sur une distribution de Tweedie restreinte. Par ailleurs, ils intègrent des informations nodales, telles que la distance géographique entre les pays, et prennent en compte l'effet dynamique de ces informations sur les poids des arêtes. Ils démontrent notamment que, lorsque le nombre de nœuds est suffisamment élevé, l'estimation de cet effet de covariable devient indépendante des étiquettes communautaires de chaque nœud lors du calcul de l'estimateur du maximum de vraisemblance des paramètres du modèle. Ce résultat permet de concevoir un algorithme efficace en deux étapes, séparant l'estimation des effets de covariables de celle des autres paramètres. L'efficacité de la méthode proposée est attestée par des études de simulation approfondies ainsi que par une application aux données du commerce international.

1 Introduction

1.1 Background

A community can be conceptualized as a collection of nodes that exhibit similar connection patterns in a network. Community detection is a fundamental problem in network analysis, with wide applications in social networks (Bedi and Sharma, 2016), marketing (Bakhthemmat and Izadi, 2021), recommendation systems (Gasparetti et al., 2021), and political polarization detection (Guerrero-Solé, 2017). Identifying communities in a network not only enables nodes to be clustered according to their connections with each other, but also reveals the hierarchical structure that many real-world networks exhibit. Furthermore, it can facilitate network data processing, analysis, and storage (Lu et al., 2018).

Among various methods for detecting communities in a network, the stochastic block model (SBM) stands out as a probabilistic graph model. It is founded based on the stochastic equivalence assumption, positing that the connecting probability between node i $$ i $$ and node j $$ j $$ depends solely on their community memberships (Holland et al., 1983). We assume that given the community memberships of two nodes i $$ i $$ and j $$ j $$ , denoted by c i $$ {c}_i $$ and c j $$ {c}_j $$ , the edge weight between them is Bernoulli distributed. In particular, letting Y i j $$ {Y}_{ij} $$ denote this weight, the adjacency matrix Y = ( Y i j ) $$ Y=\left({Y}_{ij}\right) $$ is generated as
Y i j | c i = k , c j = ℓ ∼ Bernoulli ( B k ℓ ) , $$ {Y}_{ij}\kern.15em \mid \kern.15em {c}_i=k,{c}_j=\ell \sim \mathrm{Bernoulli}\left({B}_{k\mathit{\ell}}\right), $$ (1)
where B k ℓ $$ {B}_{k\mathit{\ell}} $$ denotes the probability of connectivity between the nodes from the k th $$ k\mathrm{th} $$ and ℓ th $$ \ell \mathrm{th} $$ communities.

As indicated in the assumption labelled (1), an SBM provides an interpretable representation of the network's community structure. Moreover, an SBM can be efficiently fitted with various algorithms, such as maximum likelihood estimation and Bayesian inference (Lee and Wilkinson, 2019). In recent years, there has been extensive research into the theoretical properties of the estimators obtained from these algorithms (Lee and Wilkinson, 2019).

In this paper, we are motivated to leverage the capability of the SBM in detecting latent community structures to tackle an interesting problem—clustering countries into different groups based on their international trading patterns. However, in this application we encounter three fundamental challenges that cannot be addressed by existing SBM models.

1.2 Three main challenges

1.2.1 Edge weights

The classical SBM, as originally proposed by Holland et al. (1983), is primarily designed for binary networks, as indicated in assumption (1). However, in the context of the international trading network, we are presented with richer data, encompassing not only the presence or absence of trading relations between countries but also the specific trading volumes in dollars. These trading volumes serve as the intensity and strength of the trading relationships between countries. In such cases, thresholding the data to form a binary network would inevitably result in a loss of valuable information.

In the literature, several methods have been developed to extend the modelling of edge weights beyond the binary range. Some methods leverage distributions capable of handling edge weights. For instance, Aicher et al. (2013, 2015) adopted a Bayesian approach to model edge weights using distributions from the exponential family. Ludkin (2020) allowed for arbitrary distributions in modelling edge weights and sampled the posterior distribution using a reversible jump Markov Chain Monte Carlo method. Ng and Murphy (2021) and Motalebi et al. (2021) used a compound Bernoulli-Gamma distribution and a Hurdle model to represent edge weights, respectively. Haj et al. (2022) applied the binomial distribution to networks with integer-valued edge weights that are bounded from above. Moreover, there is a growing interest in multilayer networks, where edge weights are aggregated across network layers. Notable examples of research in this area include the work by MacDonald et al. (2022) and Chen and Mo (2022).

However, the above approaches cannot properly deal with financial data that involve nonnegative continuous random variables with a large number of zeros and a right-skewed distribution.

1.2.2 Incorporating nodal information

Many SBMs assume that nodes within the same community exhibit stochastic equivalence. However, this assumption can be restrictive and unrealistic, as real-world networks are influenced by environmental factors, individual node characteristics, and edge properties, leading to heterogeneity among community members that affects network formation. Depending on the relationship between communities and covariates, there are generally three classes of models, as shown in Figure 1. Models (b) and (c) have been previously discussed in Huang et al. (2023). We are particularly interested in model (c), where latent community labels and covariates jointly shape the network structure. In our study of international trading networks, factors such as the geographical distance between countries, along with community labels, play critical roles in shaping trading relations. Neglecting these influential factors can significantly compromise the accuracy of SBM estimation.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Three network models with covariates. The symbols X $$ X $$ , Y $$ Y $$ , and c $$ c $$ represent covariates, network connection, and community memberships, respectively. A shaded/unshaded cell means the corresponding quantity is observable/latent. (a) Covariates-driven, (b) covariates-confounding, (c) covariates-adjusted.

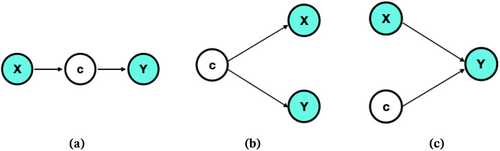
Various investigators have considered the incorporation of nodal information. For instance, Roy et al. (2019) and Choi et al. (2012) considered a pairwise covariate effect in the logistic link function when modelling the edge between two nodes. In contrast, Ma et al. (2020) and Hoff et al. (2002) incorporated the pairwise covariate effect but with a latent space model. Other research considering covariates in an SBM includes Tallberg (2004), Vu et al. (2013) and Peixoto (2018). Moreover, Mariadassou et al. (2010) and Huang et al. (2023) addressed the dual challenge of incorporating the covariates and modelling the edge weights by assuming that each integer-valued edge weight follows a Poisson distribution and accounting for the pairwise covariates in the mean structure.

While the aforementioned literature has made significant progress in incorporating covariate information into network modelling, the complexity escalates when we confront the third challenge—the observed network is changing over time. This challenge necessitates a deeper exploration of how covariates influence network formation dynamically—a facet that remains unaddressed in the existing literature.

1.2.3 Dynamic network

Recent advances in capturing temporal network data demand the extension of classic SBMs to dynamic settings, as previous research predominantly focused on static networks.

Researchers have attempted to adapt SBMs to dynamic settings, employing various strategies such as state-space models, hidden Markov chains, and change point detection. Fu et al. (2009) and Xing et al. (2010) extended a mixed membership SBM for static networks to dynamic networks by characterizing the evolving community memberships and block connection probabilities with a state space model. Both Yang et al. (2011) and Xu and Hero (2014) studied a sequence of SBMs, where the parameters were dynamically linked by a hidden Markov chain. Matias and Miele (2017) applied Markov chains to the evolution of the node community labels over time. Bhattacharjee et al. (2020) proposed a method to detect a single change point such that the community connection probabilities are different constants within the two intervals separated by it. Xin et al. (2017) characterized the occurrence of a connection between any two nodes in an SBM using an inhomogeneous Poisson process. Zhang et al. (2020) proposed a regularization method for estimating the network parameters at adjacent time points to achieve smoothness.

1.3 Our contributions

The main contribution of this paper is to extend the classical SBM to address the three challenges mentioned above. Given the community membership of each node, we generalize the assumption that edges in the network follow Bernoulli distributions to one where they follow compound Poisson-Gamma distributions instead (Section 2). This allows us to model edges that can take on any nonnegative real value, including exactly zero itself. In Section 6, we apply the proposed model to an international trading network, where each edge between two countries represents the dollar amount of their trading values, for which our model is more appropriate than the classical one. Moreover, not only do we incorporate nodal information in the form of covariates, we also allow the effects of these covariates to be time-varying (Section 2).

We use a variational approach (Section 4) to conduct statistical inference for such a time-varying network. We also prove an interesting result (Section 3) that, asymptotically, the covariate effects in our model can be estimated irrespective of how community labels are assigned to each node. This result enables us to use an efficient two-step algorithm (Section 4), separating the estimation of the covariate effects and that of the other parameters—including the unknown community labels. A similar two-step procedure is also used by Huang et al. (2023).

2 Methodology

In this section, we first give a brief review of the Tweedie distribution, which can be used to model network edges with zero or positive continuous weights. Next, we propose a general SBM using the Tweedie distribution in three successive steps, each addressing one of the challenges mentioned in Section 1.2. More specifically, we start with a vanilla model, a variation of the classic SBM where each edge value between two nodes now follows the Tweedie distribution rather than the Bernoulli distribution. We then incorporate covariate terms into the model, before finally arriving at a time-varying version of the model by allowing the covariates to have dynamic effects that change over time.

2.1 The Tweedie distribution

Let N $$ N $$ be a random variable following the Poisson distribution with mean λ $$ \lambda $$ , conditional on N = n $$ N=n $$ , Z 1 , … , Z n ˜ i i d 𝒢 ( α , σ ) where α $$ \alpha $$ and σ $$ \sigma $$ are the shape and scale parameters of the Gamma distribution, respectively. Define
Y = 0 , if N = 0 , Z 1 + Z 2 + ⋯ + Z N , if N ∈ ℕ . $$ Y=\left\{\begin{array}{ll}0,\kern2.20em & \kern1em \mathrm{if}\kern1em N=0,\\ {}{Z}_1+{Z}_2+\cdots +{Z}_N,& \kern1em \mathrm{if}\kern1em N\in \mathbb{N}.\end{array}\right. $$
Then Y $$ Y $$ has a compound Poisson-Gamma distribution, with a nonzero probability mass at 0. As Y = 0 $$ Y=0 $$ if and only if N = 0 $$ N=0 $$ , ℙ ( Y = 0 ) = ℙ ( N = 0 ) = exp ( − λ ) $$ \mathbb{P}\left(Y=0\right)=\mathbb{P}\left(N=0\right)=\exp \left(-\lambda \right) $$ . Conditional on N = n > 0 $$ N=n>0 $$ , Y $$ Y $$ follows a Gamma distribution with mean n α σ $$ n\alpha \sigma $$ and variance n α σ 2 $$ n\alpha {\sigma}^2 $$ . In the context of international trading (see also Section 6 below), N $$ N $$ may be the number of trades in a given year; Z 1 , … , Z N $$ {Z}_1,\dots, {Z}_N $$ may be the dollar amount of each trade, and then Y $$ Y $$ represents the total amount traded in that year.

The compound Poisson-Gamma distribution, known as a special case of the Tweedie distribution (Tweedie, 1984), is related to an exponential dispersion (ED) family. If Y $$ Y $$ follows an ED family distribution with mean μ $$ \mu $$ and variance function V $$ V $$ , then var ( Y ) = ϕ V ( μ ) $$ \operatorname{var}(Y)=\phi V\left(\mu \right) $$ for some dispersion parameter ϕ $$ \phi $$ . The Tweedie distribution belongs to the ED family with V ( μ ) = μ ρ $$ V\left(\mu \right)={\mu}^{\rho } $$ for some constant ρ $$ \rho $$ . Specified by different values of ρ $$ \rho $$ , the Tweedie distribution includes the normal ( ρ = 0 $$ \rho =0 $$ ), the Gamma ( ρ = 2 $$ \rho =2 $$ ), the inverse Gaussian ( ρ = 3 $$ \rho =3 $$ ), and the scaled Poisson ( ρ = 1 $$ \rho =1 $$ ). Tweedie distributions exist for all values of ρ $$ \rho $$ outside ( 0 , 1 ) $$ \left(0,1\right) $$ . Of special interest to us here is the restricted Tweedie distribution with 1 < ρ < 2 $$ 1<\rho <2 $$ , which is the aforementioned compound Poisson-Gamma distribution with a positive mass at zero but a continuous distribution of positive values elsewhere. We use the word “restricted” to indicate that ρ $$ \rho $$ is constrained to lie in ( 1 , 2 ) $$ \left(1,2\right) $$ in this Tweedie distribution. In Section 4 it will become clear that this restriction simplifies the overall estimation procedure.

Specifically, the aforementioned compound Poisson-Gamma distribution, characterized by parameters ( λ , α , σ ) $$ \left(\lambda, \alpha, \sigma \right) $$ where λ $$ \lambda $$ is the Poisson rate and ( α , σ ) $$ \left(\alpha, \sigma \right) $$ are the shape and scale parameters of the Gamma distribution, can be reparameterized as a restricted Tweedie distribution, Tw ( μ , ϕ , ρ ) $$ \left(\mu, \phi, \rho \right) $$ , with parameters ( μ , ϕ , ρ ) $$ \left(\mu, \phi, \rho \right) $$ satisfying 1 < ρ < 2 $$ 1<\rho <2 $$ and the following relationships (Tweedie, 1984; Dunn and Smyth, 2005):
λ = μ 2 − ρ ϕ ( 2 − ρ ) , α = 2 − ρ ρ − 1 , σ = ϕ ( ρ − 1 ) μ ρ − 1 . $$ \lambda =\frac{\mu^{2-\rho }}{\phi \left(2-\rho \right)},\kern1em \alpha =\frac{2-\rho }{\rho -1},\kern1em \sigma =\phi \left(\rho -1\right){\mu}^{\rho -1}. $$
Then the resulting distribution of Y $$ Y $$ can be re-expressed as
f ( y | μ , ϕ , ρ ) = a ( y , ϕ , ρ ) · exp 1 ϕ y μ 1 − ρ 1 − ρ − μ 2 − ρ 2 − ρ , $$ f\left(y\kern.15em |\kern.15em \mu, \phi, \rho \right)=a\left(y,\phi, \rho \right)\cdotp \exp \left\{\frac{1}{\phi}\left(\frac{y{\mu}^{1-\rho }}{1-\rho }-\frac{\mu^{2-\rho }}{2-\rho}\right)\right\}, $$ (2)
where y ∈ [ 0 , + ∞ ) $$ y\in \left[0,+\infty \right) $$ and 1 < ρ < 2 $$ 1<\rho <2 $$ , with
a ( y , ϕ , ρ ) = 1 y ∑ j = 1 ∞ y j α ( ρ − 1 ) j α ϕ j ( 1 + α ) ( 2 − ρ ) j j ! Γ ( j α ) , for y > 0 , 1 , for y = 0 . $$ a\left(y,\phi, \rho \right)=\left\{\begin{array}{ll}\frac{1}{y}\sum \limits_{j=1}^{\infty}\frac{y^{j\alpha}}{{\left(\rho -1\right)}^{j\alpha}{\phi}^{j\left(1+\alpha \right)}{\left(2-\rho \right)}^jj!\Gamma \left( j\alpha \right)},& \kern1em \mathrm{for}\kern1em y>0,\\ {}1,\kern15.60em & \kern1em \mathrm{for}\kern1em y=0.\end{array}\right. $$

2.2 The vanilla model

Let G = ( V , E ) $$ G=\left(V,E\right) $$ denote a weighted graph, where V $$ V $$ represents a set of nodes with cardinality | V | = n $$ \mid V\mid =n $$ and E $$ E $$ denotes the set of edges between the nodes. For SBMs, each node in the network can belong to one of K $$ K $$ non-overlapping groups. Throughout this paper, we assume that the number of groups K $$ K $$ is pre-specified. When K $$ K $$ is unknown, how to determine its “right” value is an active research problem on its own (e.g., Lei, 2016; Ma et al., 2021; Le and Levina, 2022; Wang et al., 2023). While there is no universal consensus on how to make this decision, a very common practice is to rely on the Bayesian information criterion or some of its variants. Instead of adopting this approach, for the real-data analysis in Section 6, we will simply report results for a few different choices of K $$ K $$ . In fact, we think this is more informative for real problems anyway, as we do not really believe there is just one “right” answer. Let c i ∈ { 1 , … , K } $$ {c}_i\in \left\{1,\dots, K\right\} $$ denote the unobserved community membership of node i $$ i $$ ; it follows a multinomial distribution with the probability π = ( π 1 , … , π K ) $$ \pi =\left({\pi}_1,\dots, {\pi}_K\right) $$ .

Usually, E $$ E $$ is represented by an n × n $$ n\times n $$ matrix Y = [ y i j ] ∈ ℝ n × n $$ \mathbf{Y}=\left[{y}_{ij}\right]\in {\mathbb{R}}^{n\times n} $$ . In classical SBMs, each y i j $$ {y}_{ij} $$ is modelled either as a Bernoulli random variable taking on binary values of 0 or 1, or as a Poisson random variable taking on nonnegative integer values. We first relax this restriction by allowing y i j $$ {y}_{ij} $$ to take on nonnegative real values. Since we focus on undirected weighted networks without self-loops, for us Y $$ \mathbf{Y} $$ is a symmetric matrix with nonnegative, real-valued entries and zeros on the diagonal.

Given the observed dataset D = { y i j } 1 ≤ i < j ≤ n $$ D={\left\{{y}_{ij}\right\}}_{1\le i<j\le n} $$ , we assume that each y i j $$ {y}_{ij} $$ follows a restricted Tweedie distribution
y i j ∼ Tw ( μ i j , ϕ , ρ ) , 1 < ρ < 2 , $$ {y}_{ij}\sim \mathrm{Tw}\left({\mu}_{ij},\phi, \rho \right),\kern1em 1<\rho <2, $$ (3)
where the mean μ i j $$ {\mu}_{ij} $$ is modelled as a positive constant determined by the latent community label of nodes i $$ i $$ and j $$ j $$ through a log-link function, i.e.,
log ( μ i j ) = β 0 k ℓ , if c i = k and c j = ℓ , $$ \log \left({\mu}_{ij}\right)={\beta}_0^{k\mathit{\ell}},\kern1em \mathrm{if}\kern1em {c}_i=k\kern1em \mathrm{and}\kern1em {c}_j=\ell, $$ (4)
where β 0 = [ β 0 k ℓ ] ∈ ℝ K × K $$ {\beta}_0=\left[{\beta}_0^{k\mathit{\ell}}\right]\in {\mathbb{R}}^{K\times K} $$ is a symmetric matrix. For a constant model, the log-link may not appear to be necessary, but it will become more useful when we incorporate covariates into this baseline model.

2.3 A model with covariates

In many real-life situations, we observe additional information about the network. For example, in addition to the relative existence or importance of each edge, a collection of p $$ p $$ symmetric covariate matrices X ( 1 ) , … , X ( p ) ∈ ℝ n × n $$ {\mathbf{X}}^{(1)},\dots, {\mathbf{X}}^{(p)}\in {\mathbb{R}}^{n\times n} $$ may also be available, where the ( i , j ) $$ \left(i,j\right) $$ -th entry x i j ( u ) $$ {x}_{ij}^{(u)} $$ of each X ( u ) $$ {\mathbf{X}}^{(u)} $$ represents a pairwise covariate containing some information about the connection between node i $$ i $$ and node j $$ j $$ , and x i i ( u ) = 0 $$ {x}_{ii}^{(u)}=0 $$ for i ∈ { 1 , … , n } $$ i\in \left\{1,\dots, n\right\} $$ and u ∈ { 1 , … , p } $$ u\in \left\{1,\dots, p\right\} $$ . Given a dataset D = { Y , X ( 1 ) , … , X ( p ) } $$ D=\left\{\mathbf{Y},{\mathbf{X}}^{(1)},\dots, {\mathbf{X}}^{(p)}\right\} $$ , the vanilla model from Section 2.2 can be easily extended by replacing statement (4) with
log ( μ i j ) = β 0 k ℓ + x i j ⊤ β , if c i = k and c j = ℓ , $$ \log \left({\mu}_{ij}\right)={\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta}, \kern1em \mathrm{if}\kern1em {c}_i=k\kern1em \mathrm{and}\kern1em {c}_j=\ell, $$ (5)
so that μ i j $$ {\mu}_{ij} $$ is affected not only by the community labels c i , c j $$ {c}_i,{c}_j $$ but also by the covariates contained in x i j $$ {\boldsymbol{x}}_{ij} $$ . Here, both x i j ≡ ( x i j ( 1 ) , … , x i j ( p ) ) ⊤ $$ {\boldsymbol{x}}_{ij}\equiv {\left({x}_{ij}^{(1)},\dots, {x}_{ij}^{(p)}\right)}^{\top } $$ and β $$ \boldsymbol{\beta} $$ are p $$ p $$ -dimensional vectors.

2.4 A time-varying model

Now suppose we observe an evolving network at a series of T $$ T $$ discrete time points { t 1 , … , t T } $$ \left\{{t}_1,\dots, {t}_T\right\} $$ , with a common set of n $$ n $$ nodes. Specifically, our dataset is of the form D = { Y ( t 1 ) , … , Y ( t T ) ; X ( 1 ) , … , X ( p ) } $$ D=\left\{\mathbf{Y}\left({t}_1\right),\dots, \mathbf{Y}\left({t}_T\right);{\mathbf{X}}^{(1)},\dots, {\mathbf{X}}^{(p)}\right\} $$ . Without loss of generality, we assume t ν ∈ [ 0 , 1 ] $$ {t}_{\nu}\in \left[0,1\right] $$ for ν ∈ { 1 , … , T } $$ \nu \in \left\{1,\dots, T\right\} $$ .

To model such data, we assume that the latent community labels c 1 , … , c n $$ {c}_1,\dots, {c}_n $$ are fixed over time but allow the covariate effects to change over time through a varying-coefficient model. In reality, the community labels may also change over time, but a fundamentally different set of tools will be required to model these changes and we will study them separately—not in this paper. Here we simply assume that the model specified in statement (3) holds pointwise at every time point t $$ t $$ , i.e.,
y i j ( t ) ∼ Tw ( μ i j ( t ) , ϕ , ρ ) , 1 < ρ < 2 , $$ {y}_{ij}(t)\sim \mathrm{Tw}\left({\mu}_{ij}(t),\phi, \rho \right),\kern1em 1<\rho <2, $$ (6)
and
log { μ i j ( t ) } = β 0 k ℓ + x i j ⊤ β ( t ) , if c i = k and c j = ℓ , $$ \log \left\{{\mu}_{ij}(t)\right\}={\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} (t),\kern1em \mathrm{if}\kern1em {c}_i=k\kern1em \mathrm{and}\kern1em {c}_j=\ell, $$ (7)
where β ( t ) ≡ ( β 1 ( t ) , … , β p ( t ) ) ⊤ $$ \boldsymbol{\beta} (t)\equiv {\left({\beta}_1(t),\dots, {\beta}_p(t)\right)}^{\top } $$ and each β u ( t ) $$ {\beta}_u(t) $$ is a smooth function of time. The full likelihood function corresponding to our time-varying model identified in statements (6) and (7) is given by
L ( β 0 , β ( t ) , π , ϕ , ρ ; D , c ) = ∏ i = 1 n ∏ k = 1 K π k 1 ( c i = k ) ∏ ν = 1 T ∏ 1 ≤ i < j ≤ n ∏ k , ℓ = 1 K a ( y i j ( t ν ) , ϕ , ρ ) × exp 1 ϕ y i j ( t ν ) exp [ ( 1 − ρ ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] 1 − ρ − exp [ ( 2 − ρ ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] 2 − ρ 1 ( c i = k , c j = ℓ ) . $$ {\displaystyle \begin{array}{ll}\hfill L\left({\beta}_0,\boldsymbol{\beta} (t),\pi, \phi, \rho; D,c\right)& =\prod \limits_{i=1}^n\prod \limits_{k=1}^K{\pi}_k^{\mathbbm{1}\left({c}_i=k\right)}\prod \limits_{\nu =1}^T\prod \limits_{1\le i<j\le n}\prod \limits_{k,\ell =1}^K\left[a\Big({y}_{ij}\left({t}_{\nu}\right),\phi, \rho \Big)\right.\\ {}\hfill & \kern1em \times \exp \left\{\frac{1}{\phi}\left(\frac{y_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-\rho \right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{1-\rho }-\right.\right.\\ {}\hfill & \kern5em {\left.\left.\left.\frac{\exp \left[\left(2-\rho \right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{2-\rho}\right)\right\}\right]}^{\mathbbm{1}\left({c}_i=k,{c}_j=\ell \right)}.\end{array}} $$ (8)

The likelihood functions for the vanilla model (Section 2.2) and for the static model with covariates (Section 2.3) are simply special cases of equation (8).

3 Theory

The log-likelihood based on equation (8) contains three additive terms: the first involves only π $$ \pi $$ ; the second involves only ( ϕ , ρ ) $$ \left(\phi, \rho \right) $$ ; and the third is the only term that involves both β 0 $$ {\beta}_0 $$ and β ( t ) $$ \boldsymbol{\beta} (t) $$ . Define
ℓ n ( β ( t ) , ϕ 0 , ρ 0 ; D , z ) ≡ 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n ∑ k , l = 1 K 1 ( z i = k , z j = ℓ ) ϕ 0 × y i j ( t ν ) exp [ ( 1 − ρ 0 ) { β ^ 0 k l ( β ( t ν ) ) + x i j ⊤ β ( t ν ) } ] 1 − ρ 0 − exp [ ( 2 − ρ 0 ) { β ^ 0 k l ( β ( t ν ) ) + x i j ⊤ β ( t ν ) } ] 2 − ρ 0 $$ {\displaystyle \begin{array}{ll}\hfill {\ell}_n\left(\boldsymbol{\beta} (t),{\phi}_0,{\rho}_0;D,z\right)& \equiv \frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\sum \limits_{k,l=1}^K\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\\ {}\hfill & \kern1em \times \left(\frac{y_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-{\rho}_0\right)\left\{{\hat{\beta}}_0^{kl}\left(\boldsymbol{\beta} \left({t}_{\nu}\right)\right)+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{1-{\rho}_0}-\right.\\ {}\hfill & \kern3em \left.\frac{\exp \left[\left(2-{\rho}_0\right)\left\{{\hat{\beta}}_0^{kl}\left(\boldsymbol{\beta} \left({t}_{\nu}\right)\right)+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{2-{\rho}_0}\right)\end{array}} $$ (9)
to be the aforementioned third term after having
  • •

    replaced the unknown labels c = ( c 1 , … , c n ) $$ c=\left({c}_1,\dots, {c}_n\right) $$ with an arbitrary set of labels z = ( z 1 , … , z n ) $$ z=\left({z}_1,\dots, {z}_n\right) $$ , where each z i $$ {z}_i $$ is independently multinomial with probability ( p 1 , … , p K ) $$ \left({p}_1,\dots, {p}_K\right) $$ ;

  • •

    profiled out the parameter β 0 $$ {\beta}_0 $$ by replacing it with β ^ 0 ( β ( t ) ) $$ {\hat{\beta}}_0\left(\boldsymbol{\beta} (t)\right) $$ , while presuming ϕ = ϕ 0 $$ \phi ={\phi}_0 $$ and ρ = ρ 0 $$ \rho ={\rho}_0 $$ to be known and fixed; and

  • •

    re-scaled it by the total number of pairs, n 2 $$ \left(\genfrac{}{}{0ex}{}{n}{2}\right) $$ .

This quantity identified in equation (9) turns out to be very interesting. Not only does β ^ 0 ( β ( t ) ) $$ {\hat{\beta}}_0\left(\boldsymbol{\beta} (t)\right) $$ have an explicit expression, but the function identified in equation (9) itself can also be shown to converge to a quantity not dependent on z $$ z $$ as n $$ n $$ tends to infinity.

In other words, it does not matter that z $$ z $$ is a set of arbitrarily assigned labels! This has immediate computational implications (see Section 4). Some high-level details of this theory are spelled out below in Section 3.1, while actual proofs are given in Appendix B.

3.1 Details

To simplify the notation, we first define two population parameters,
θ = ∑ ν = 1 T 𝔼 [ y i j ( t ν ) exp { ( 1 − ρ 0 ) x i j ⊤ β ( t ν ) } ] and γ = ∑ ν = 1 T 𝔼 [ exp { ( 2 − ρ 0 ) x i j ⊤ β ( t ν ) } ] .
For these to be properly defined, we require the following two conditions, which are fairly standard and not fundamentally restrictive.

Condition 3.1.The covariates { x i j , 1 ≤ i < j ≤ n } $$ \left\{{\boldsymbol{x}}_{ij},1\le i<j\le n\right\} $$ are i.i.d., and there exists some α > 0 $$ \alpha >0 $$ such that ℙ ( exp { x i j ⊤ u } ≥ δ ) ≤ 2 exp ( − δ 2 / α ) $$ \mathbb{P}\left(\exp \left\{{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{u}\right\}\ge \delta \right)\le 2\exp \left(-{\delta}^2/\alpha \right) $$ for any δ > 0 $$ \delta >0 $$ , i ≠ j $$ i\ne j $$ and u ∈ ℝ p $$ \boldsymbol{u}\in {\mathbb{R}}^p $$ satisfying ‖ u ‖ 2 = u 1 2 + ⋯ + u p 2 = 1 $$ {\left\Vert \boldsymbol{u}\right\Vert}_2=\sqrt{u_1^2+\cdots +{u}_p^2}=1 $$ .

Condition 3.2.The function β u ( t ) $$ {\beta}_u(t) $$ is continuous on [ 0 , 1 ] $$ \left[0,1\right] $$ , for all u ∈ { 1 , … , p } $$ u\in \left\{1,\dots, p\right\} $$ .

The corresponding empirical versions of θ $$ \theta $$ and γ $$ \gamma $$ between any two groups, k $$ k $$ and ℓ $$ \ell $$ , according to an arbitrary community label assignment, z $$ z $$ , are given by
θ ^ k ℓ = 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n y i j ( t ν ) exp [ ( 1 − ρ 0 ) x i j ⊤ β ( t ν ) ] 1 ( z i = k , z j = ℓ ) , γ ^ k ℓ = 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n exp [ ( 2 − ρ 0 ) x i j ⊤ β ( t ν ) ] 1 ( z i = k , z j = ℓ ) . $$ {\displaystyle \begin{array}{ll}\hfill {\hat{\theta}}_{k\mathit{\ell}}& =\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}{y}_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-{\rho}_0\right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right),\\ {}\hfill {\hat{\gamma}}_{k\mathit{\ell}}& =\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\exp \left[\left(2-{\rho}_0\right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right).\end{array}} $$
We can then establish the following main theorem.

Theorem 1.As n → ∞ $$ n\to \infty $$ while K $$ K $$ remains constant,

ℓ n ( β ( t ) , ϕ 0 , ρ 0 ; D , z ) = 1 ϕ 0 1 ( 1 − ρ 0 ) ( 2 − ρ 0 ) ∑ k , ℓ = 1 K θ ^ k ℓ 2 − ρ 0 · γ ^ k ℓ ρ 0 − 1 = 1 ϕ 0 1 ( 1 − ρ 0 ) ( 2 − ρ 0 ) θ 2 − ρ 0 · γ ρ 0 − 1 + o p ( 1 ) . $$ {\displaystyle \begin{array}{ll}\hfill {\ell}_n\left(\boldsymbol{\beta} (t),{\phi}_0,{\rho}_0;D,z\right)& =\frac{1}{\phi_0}\frac{1}{\left(1-{\rho}_0\right)\left(2-{\rho}_0\right)}\sum \limits_{k,\ell =1}^K{\hat{\theta}}_{k\mathit{\ell}}^{2-{\rho}_0}\cdotp {\hat{\gamma}}_{k\mathit{\ell}}^{\rho_0-1}\\ {}\hfill & =\frac{1}{\phi_0}\frac{1}{\left(1-{\rho}_0\right)\left(2-{\rho}_0\right)}{\theta}^{2-{\rho}_0}\cdotp {\gamma}^{\rho_0-1}+{o}_p(1).\end{array}} $$ (10)

Remark 1.So far, we have simply written θ ^ k ℓ $$ {\hat{\theta}}_{k\mathit{\ell}} $$ , γ ^ k ℓ $$ {\hat{\gamma}}_{k\mathit{\ell}} $$ , θ $$ \theta $$ and γ $$ \gamma $$ in order to keep the notation short. To better appreciate the conclusion of the theorem, however, it is perhaps important for us to emphasize here that these quantities are more properly written as θ ^ k ℓ ( β ( t ) , ρ 0 ; D , z ) $$ {\hat{\theta}}_{k\mathit{\ell}}\left(\boldsymbol{\beta} (t),{\rho}_0;D,z\right) $$ , γ ^ k ℓ ( β ( t ) , ρ 0 ; D , z ) $$ {\hat{\gamma}}_{k\mathit{\ell}}\left(\boldsymbol{\beta} (t),{\rho}_0;D,z\right) $$ , θ ( β ( t ) , ρ 0 ; D ) $$ \theta \left(\boldsymbol{\beta} (t),{\rho}_0;D\right) $$ , and γ ( β ( t ) , ρ 0 ; D ) $$ \gamma \left(\boldsymbol{\beta} (t),{\rho}_0;D\right) $$ .

The implication of Theorem 1 is that, asymptotically, our inference about β ( t ) $$ \boldsymbol{\beta} (t) $$ is not affected by the community labels—nor is it affected by the total number of communities, K $$ K $$ , since z $$ z $$ can follow any multinomial distributions with probabilities ( p 1 , … , p K ) $$ \left({p}_1,\dots, {p}_K\right) $$ , including those with some p k = 0 $$ {p}_k=0 $$ . Thus, even if we got K $$ K $$ wrong, our inference about β ( t ) $$ \boldsymbol{\beta} (t) $$ would still be correct.

4 Estimation method

4.1 Two-step estimation

In this section, we outline an algorithm to fit the restricted Tweedie SBM. Since, for us, the parameter ρ $$ \rho $$ is restricted to the interval ( 1 , 2 ) $$ \left(1,2\right) $$ , we find it sufficient to simply perform a grid search (e.g., Dunn and Smyth, 2005, 2008; Lian et al., 2023) over an equally spaced sequence, say, 1 < ρ 1 < ⋯ < ρ m < 2 $$ 1<{\rho}_1<\cdots <{\rho}_m<2 $$ , to determine its “optimal” value. However, our empirical experiences also indicate that a sufficiently accurate estimate of ρ $$ \rho $$ is important for making correct inferences on other quantities of interest, including the latent community labels c $$ c $$ .

For any given ρ 0 $$ {\rho}_0 $$ in a pre-specified sequence/grid, we propose an efficient two-step algorithm to estimate the other parameters. In Step 1 (Section 4.1.1), we obtain an estimate β ^ ρ 0 ( t ) $$ {\hat{\boldsymbol{\beta}}}_{\rho_0}(t) $$ of β ( t ) $$ \boldsymbol{\beta} (t) $$ using an arbitrary set of community labels. This is made possible by the theoretical result identified earlier in Section 3. In Step 2 (Section 4.1.2), we obtain estimates of the remaining parameters— β ^ 0 ( ρ 0 ) , π ^ ( ρ o ) , ϕ ^ ( ρ 0 ) $$ {\hat{\beta}}_0\left({\rho}_0\right),\hat{\pi}\left({\rho}_o\right),\hat{\phi}\left({\rho}_0\right) $$ —as well as inferred labels— ĉ ( ρ 0 ) $$ \hat{c}\left({\rho}_0\right) $$ —while keeping β ^ ρ 0 ( t ) $$ {\hat{\boldsymbol{\beta}}}_{\rho_0}(t) $$ fixed. The optimal ρ $$ \rho $$ is then chosen to be
ρ ^ = argmax ρ 0 ∈ { ρ 1 , … , ρ m } L ( β ^ 0 ( ρ 0 ) , β ^ ρ 0 ( t ) , π ^ ( ρ 0 ) , ϕ ^ ( ρ 0 ) , ρ 0 ; D , ĉ ( ρ 0 ) ) . $$ \hat{\rho}=\underset{\rho_0\in \left\{{\rho}_1,\dots, {\rho}_m\right\}}{\mathrm{argmax}}L\left({\hat{\beta}}_0\left({\rho}_0\right),{\hat{\boldsymbol{\beta}}}_{\rho_0}(t),\hat{\pi}\left({\rho}_0\right),\hat{\phi}\left({\rho}_0\right),{\rho}_0;D,\hat{c}\left({\rho}_0\right)\right). $$

4.1.1 Step 1: Estimating the covariate coefficients

It is clear from Theorem 1 in Section 3 that, when ρ = ρ 0 $$ \rho ={\rho}_0 $$ is given and fixed, the log-likelihood function identified in expression (9) serves as an objective function for estimating β ( t ) $$ \boldsymbol{\beta} (t) $$ . To begin, here one can fix the parameter ϕ $$ \phi $$ at ϕ 0 = 1 $$ {\phi}_0=1 $$ , since it only appears as a scaling constant in ℓ n ( · ) $$ {\ell}_n\left(\cdotp \right) $$ and the maximizer β ( t ) $$ \boldsymbol{\beta} (t) $$ is not affected. The main computational saving afforded by Theorem 1 is that we can use an arbitrary set of labels z $$ z $$ to carry out this step, estimating β ( t ) $$ \boldsymbol{\beta} (t) $$ separately without simultaneously concerning ourselves with β 0 $$ {\beta}_0 $$ or having to make inference on c $$ c $$ . Both of those tasks can be temporarily delayed until after β ( t ) $$ \boldsymbol{\beta} (t) $$ has been estimated.

For our static model (Section 2.3), we use the optim function in R to maximize the function ℓ n ( · ) $$ {\ell}_n\left(\cdotp \right) $$ directly over β $$ \boldsymbol{\beta} $$ , with T = 1 $$ T=1 $$ . For our time-varying model (Section 2.4), we add (component-wise) smoothness penalties to ℓ n ( · ) $$ {\ell}_n\left(\cdotp \right) $$ and estimate β ( t ) $$ \boldsymbol{\beta} (t) $$ as
β ^ ρ 0 ( t ) = argmax β u ( t ) ∈ ℬ ℓ n ( β ( t ) , 1 , ρ 0 ; D , z ) − 1 2 ∑ u = 1 p ξ u · ∫ { β u ′ ′ ( t ) } 2 d t , $$ {\hat{\boldsymbol{\beta}}}_{\rho_0}(t)=\underset{{\boldsymbol{\beta}}_u(t)\in \mathcal{B}}{\mathrm{argmax}}\kern0.3em {\ell}_n\left(\boldsymbol{\beta} (t),1,{\rho}_0;D,z\right)-\frac{1}{2}\sum \limits_{u=1}^p{\xi}_u\cdotp \int {\left\{{\boldsymbol{\beta}}_u^{\prime \prime }(t)\right\}}^2 dt, $$ (11)
where ℬ $$ \mathcal{B} $$ is chosen as the class of functions that are Hölder continuous (Stone, 1985). According to Stone (1985), each β u $$ {\beta}_u $$ can be well approximated by spline functions, which are defined as follows. Let 0 = κ 0 < κ 1 < ⋯ < κ J < κ J + 1 = 1 $$ 0={\kappa}_0<{\kappa}_1<\cdots <{\kappa}_J<{\kappa}_{J+1}=1 $$ be a sequence of knots that constitute a partition on [ 0 , 1 ] $$ \left[0,1\right] $$ . Given a positive integer m $$ m $$ , a spline function h $$ h $$ satisfies the following conditions: (i) at each subinterval [ κ j , κ j + 1 ] $$ \left[{\kappa}_j,{\kappa}_{j+1}\right] $$ where j ∈ { 0 , … , J } $$ j\in \left\{0,\dots, J\right\} $$ , h $$ h $$ is a polynomial of degree m − 1 $$ m-1 $$ ; (ii) the derivative of h $$ h $$ of order ( m − 2 ) $$ \left(m-2\right) $$ is continuous. Moreover, there exist J + m $$ J+m $$ normalized B-spline basis functions { B j ( t ) : j ∈ { 1 , … , J + m } } $$ \left\{{B}_j(t):j\in \left\{1,\dots, J+m\right\}\right\} $$ such that h ( t ) = ∑ j = 1 J + m b j B j ( t ) $$ h(t)={\sum}_{j=1}^{J+m}{b}_j{B}_j(t) $$ for some ( b 1 , … , b J + m ) ⊤ ∈ ℝ J + m $$ {\left({b}_1,\dots, {b}_{J+m}\right)}^{\top}\in {\mathbb{R}}^{J+m} $$ . The penalty parameters ξ 1 , … , ξ p $$ {\xi}_1,\dots, {\xi}_p $$ are chosen by cross-validation (see Section 4.2 below). With given penalty parameters, the estimation of β ^ ρ 0 ( t ) $$ {\hat{\boldsymbol{\beta}}}_{\rho_0}(t) $$ is performed using B-splines, with technical details for solving expression (11) provided in the Supplementary Material.

4.1.2 Step 2: Variational inference

In Step 2, with the estimate β ^ ρ 0 ( t ) $$ {\hat{\boldsymbol{\beta}}}_{\rho_0}(t) $$ from Step 1 (and, again, a pre-fixed ρ = ρ 0 $$ \rho ={\rho}_0 $$ ), we estimate the remaining parameters β 0 $$ {\beta}_0 $$ , π $$ \pi $$ , and ϕ $$ \phi $$ , as well as make inferences on the latent label c $$ c $$ .

If we directly maximized the likelihood function identified in expression (8) using the EM algorithm, the E-step would require us to compute 𝔼 c | D ( · ) but, here, the conditional distribution of the latent variable c $$ c $$ given D $$ D $$ is complicated because c i $$ {c}_i $$ and c j $$ {c}_j $$ are not conditionally independent in general. We will use a variational approach instead.

To proceed, it will be more natural for us to emphasize the fact that the likelihood function in equation (8) is really just the joint distribution of ( D , c ) $$ \left(D,c\right) $$ . Thus, instead of writing it as L ( β 0 , β ( t ) , π , ϕ , ρ ; D , c ) $$ L\left({\beta}_0,\boldsymbol{\beta} (t),\pi, \phi, \rho; D,c\right) $$ , in this section we will write it simply as ℙ ( D , c ; β 0 , π , ϕ ) $$ \mathbb{P}\left(D,c;{\beta}_0,\pi, \phi \right) $$ , where we have also dropped β ( t ) $$ \boldsymbol{\beta} (t) $$ and ρ $$ \rho $$ to keep the notation short because, within this step, ρ = ρ 0 $$ \rho ={\rho}_0 $$ and β ( t ) = β ^ ρ 0 ( t ) $$ \boldsymbol{\beta} (t)={\hat{\boldsymbol{\beta}}}_{\rho_0}(t) $$ are both fixed and not being estimated.

Ideally, since the latent variable c $$ c $$ is not observable, one may want to work with the marginal distribution of D $$ D $$ and estimate ( β 0 , π , ϕ ) $$ \left({\beta}_0,\pi, \phi \right) $$ as:
β ^ 0 , π ^ , ϕ ^ = argmax β 0 , π , ϕ log ℙ ( D ; β 0 , π , ϕ ) = argmax β 0 , π , ϕ log ∑ c ∈ [ K ] n ℙ ( D , c ; β 0 , π , ϕ ) , $$ {\displaystyle \begin{array}{ll}\hfill \left({\hat{\beta}}_0,\hat{\pi},\hat{\phi}\right)& =\underset{\beta_0,\pi, \phi }{\mathrm{argmax}}\log \mathbb{P}\left(D;{\beta}_0,\pi, \phi \right)\\ {}\hfill & =\underset{\beta_0,\pi, \phi }{\mathrm{argmax}}\kern0.3em \log \sum \limits_{c\in {\left[K\right]}^n}\mathbb{P}\left(D,c;{\beta}_0,\pi, \phi \right),\end{array}} $$ (12)
where c = [ c 1 , … , c n ] $$ c=\left[{c}_1,\dots, {c}_n\right] $$ represents a set of latent random variables associated with vertices 1 , … , n $$ 1,\dots, n $$ , each taking values in [ K ] ≡ { 1 , … , K } $$ \left[K\right]\equiv \left\{1,\dots, K\right\} $$ . However, this optimization is difficult due to the summation over K n $$ {K}^n $$ terms. The key idea of variational inference is to approximate ℙ ( c | D ; β 0 , π , ϕ ) $$ \mathbb{P}\left(c\kern.15em |\kern.15em D;{\beta}_0,\pi, \phi \right) $$ with a distribution q ( c ) $$ q(c) $$ from a more tractable family and to decompose the objective function in expression (12) into two terms:
log ℙ ( D ; β 0 , π , ϕ ) = ∑ c ∈ [ K ] n log ℙ ( D ; β 0 , π , ϕ ) · q ( c ) = ∑ c ∈ [ K ] n log ℙ ( D ; β 0 , π , ϕ ) · q ( c ) ℙ ( D , c ; β 0 , π , ϕ ) + log ℙ ( D , c ; β 0 , π , ϕ ) q ( c ) · q ( c ) = 𝔼 q log q ( c ) ℙ ( c | D ; β 0 , π , ϕ ) ⏟ KL + 𝔼 q log ℙ ( D , c ; β 0 , π , ϕ ) q ( c ) ⏟ ELBO . (13)
The first term in equation (13) can be recognized as the Kullback–Leibler (KL) divergence between q ( c ) $$ q(c) $$ and ℙ ( c | D ; · ) $$ \mathbb{P}\left(c\kern.15em |\kern.15em D;\cdotp \right) $$ , which is nonnegative. This makes the second term in equation (13) a lower bound of the objective function. It is referred to as the “evidence lower bound” (ELBO) and is equal to the objective function itself when the first term is zero, i.e., when q ( c ) = ℙ ( c | D ; · ) $$ q(c)=\mathbb{P}\left(c\kern.15em |\kern.15em D;\cdotp \right) $$ . The distribution q ( c ) $$ q(c) $$ is also referred to as the “variational distribution” in this context.

Instead of maximizing expression (12) directly, one maximizes the ELBO term—not only over ( β 0 , π , ϕ ) $$ \left({\beta}_0,\pi, \phi \right) $$ , but also over q $$ q $$ . Since the original objective function—the left-hand side of expression (13)—does not depend on q $$ q $$ , maximizing the ELBO term over q $$ q $$ is also equivalent to minimizing the KL term. When the KL term is small, not only is the variational distribution q ( c ) $$ q(c) $$ close to ℙ ( c | D ; · ) $$ \mathbb{P}\left(c\kern.15em |\kern.15em D;\cdotp \right) $$ , but the ELBO term is also automatically close to the original objective function, which justifies why this approach often gives a good approximate solution to the otherwise intractable problem stated in expression (12) and why the variational distribution q ( c ) ≈ ℙ ( c | D ; · ) $$ q(c)\approx \mathbb{P}\left(c\kern.15em |\kern.15em D;\cdotp \right) $$ can be used to make approximate inferences about c $$ c $$ .

Since the decomposition identified in expression (13) holds for any q $$ q $$ , in practice one usually chooses it from a “convenient” family of distributions so that 𝔼 q ( · ) is easy to compute. In particular, we can choose
q ( c ) = ∏ i = 1 n q i ( c i ) $$ q(c)=\prod \limits_{i=1}^n{q}_i\left({c}_i\right) $$
to be a completely factorizable distribution; here, each q i $$ {q}_i $$ is simply a standalone multinomial distribution with probability vector ( τ i 1 , … , τ i K ) $$ \left({\tau}_{i1},\dots, {\tau}_{iK}\right) $$ . Under this choice, 𝔼 q [ 1 ( c i = k ) ] = τ i k , 𝔼 q [ 1 ( c i = k , c j = ℓ ) ] = τ i k τ j ℓ , and the ELBO term in expression (13) is simply
ELBO ( τ , β 0 , π , ϕ ; D ) = ∑ i = 1 n ∑ k = 1 K τ i k · log ( π k ) + ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n log a ( y i j ( t ν ) , ϕ , ρ 0 ) + ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n ∑ k , l = 1 K τ i k τ j ℓ ϕ ( y i j ( t ν ) exp [ ( 1 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ^ ρ 0 ( t ν ) } ] 1 − ρ 0 − exp [ ( 2 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ^ ρ 0 ( t ν ) } ] 2 − ρ 0 ) − ∑ i = 1 n ∑ k = 1 K τ i k · log ( τ i k ) , $$ {\displaystyle \begin{array}{ll}\mathrm{ELBO}\left(\tau, {\beta}_0,\pi, \phi; D\right)& =\sum \limits_{i=1}^n\sum \limits_{k=1}^K{\tau}_{ik}\cdotp \log \left({\pi}_k\right)+\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\log a\left({y}_{ij}\left({t}_{\nu}\right),\phi, {\rho}_0\right)\\ {}& \kern1em +\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\kern.2em \sum \limits_{k,l=1}^K\frac{\tau_{ik}{\tau}_{j\mathit{\ell}}}{\phi}\Big({y}_{ij}\left({t}_{\nu}\right)\frac{\exp \left[\left(1-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right\}\right]}{1-{\rho}_0}\\ {}& \kern1em -\frac{\exp \left[\left(2-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right\}\right]}{2-{\rho}_0}\Big)-\sum \limits_{i=1}^n\sum \limits_{k=1}^K{\tau}_{ik}\cdotp \log \left({\tau}_{ik}\right),\end{array}} $$ (14)
which is easy to maximize in a coordinate-wise fashion, i.e., successively over τ $$ \tau $$ , β 0 $$ {\beta}_0 $$ , π $$ \pi $$ and ϕ $$ \phi $$ .
The maximum of expression (14) with respect to τ $$ \tau $$ and π $$ \pi $$ can be found by the method of Lagrange multipliers, as there are implicit equality constraints: ∑ k = 1 K τ i k = 1 $$ {\sum}_{k=1}^K{\tau}_{ik}=1 $$ for any i $$ i $$ , and ∑ k = 1 K π k = 1 $$ {\sum}_{k=1}^K{\pi}_k=1 $$ . Specifically, at iteration step h $$ h $$ , their respective updates are
τ i k ( h ) = f i k f i 1 + ⋯ + f i K , k ∈ { 1 , … , K } and i ∈ { 1 , … , n } , $$ {\tau}_{ik}^{(h)}=\frac{f_{ik}}{f_{i1}+\cdots +{f}_{iK}},\kern0.3em k\in \left\{1,\dots, K\right\}\kern0.3em \mathrm{and}\kern0.3em i\in \left\{1,\dots, n\right\}, $$
where
f i k = π k ( h − 1 ) · exp ∑ ν = 1 T ∑ j ≠ i ∑ ℓ = 1 K τ j ℓ ( h − 1 ) ϕ ( h − 1 ) y i j ( t ) exp [ ( 1 − ρ 0 ) { ( β 0 k ℓ ) ( h − 1 ) + x i j ⊤ β ^ ρ 0 ( t ν ) } ] 1 − ρ 0 − exp [ ( 2 − ρ 0 ) { ( β 0 k ℓ ) ( h − 1 ) + x i j ⊤ β ^ ρ 0 ( t ν ) } ] 2 − ρ 0 , $$ {\displaystyle \begin{array}{ll}{f}_{ik}& ={\pi}_k^{\left(h-1\right)}\cdotp \exp \left[\sum \limits_{\nu =1}^T\sum \limits_{j\ne i}\kern.2em \sum \limits_{\ell =1}^K\frac{\tau_{j\mathit{\ell}}^{\left(h-1\right)}}{\phi^{\left(h-1\right)}}\left\{{y}_{ij}(t)\frac{\exp \left[\left(1-{\rho}_0\right)\left\{{\left({\beta}_0^{k\mathit{\ell}}\right)}^{\left(h-1\right)}+{\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right\}\right]}{1-{\rho}_0}\right.\right.\\ {}& \kern1em \left.\left.-\frac{\exp \left[\left(2-{\rho}_0\right)\left\{{\left({\beta}_0^{k\mathit{\ell}}\right)}^{\left(h-1\right)}+{\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right\}\right]}{2-{\rho}_0}\right\}\right],\end{array}} $$
and
π k ( h ) = τ 1 k ( h ) + ⋯ + τ n k ( h ) n , k ∈ { 1 , … , K } . $$ {\pi}_k^{(h)}=\frac{\tau_{1k}^{(h)}+\cdots +{\tau}_{nk}^{(h)}}{n},\kern0.3em k\in \left\{1,\dots, K\right\}. $$
The objective function identified in equation (14) is concave in β 0 k ℓ $$ {\beta}_0^{k\mathit{\ell}} $$ for each community label pair ( k , ℓ ) $$ \left(k,\ell \right) $$ . This allows us to simply update the parameter β 0 $$ {\beta}_0 $$ by solving the first-order equation ∂ ELBO ( τ ( h ) , β 0 , π ( h ) , ϕ ( h ) ; D ) / ∂ β 0 = 0 $$ \partial \mathrm{ELBO}\left({\tau}^{(h)},{\beta}_0,{\pi}^{(h)},{\phi}^{(h)};D\right)/\partial {\beta}_0=0 $$ analytically for each pair ( k , ℓ ) $$ \left(k,\ell \right) $$ , which yields:
( β 0 k ℓ ) ( h ) = log ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n y i j ( t ) exp [ ( 1 − ρ 0 ) x i j ⊤ β ^ ρ 0 ( t ν ) ] · τ i k ( h ) τ j ℓ ( h ) ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n exp [ ( 2 − ρ 0 ) x i j ⊤ β ^ ρ 0 ( t ν ) ] · τ i k ( h ) τ j ℓ ( h ) . $$ {\left({\beta}_0^{k\mathit{\ell}}\right)}^{(h)}=\log \frac{\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}{y}_{ij}(t)\exp \left[\left(1-{\rho}_0\right){\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right]\cdotp {\tau}_{ik}^{(h)}{\tau}_{j\mathit{\ell}}^{(h)}}{\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\exp \left[\left(2-{\rho}_0\right){\boldsymbol{x}}_{ij}^{\top }{\hat{\boldsymbol{\beta}}}_{\rho_0}\left({t}_{\nu}\right)\right]\cdotp {\tau}_{ik}^{(h)}{\tau}_{j\mathit{\ell}}^{(h)}}. $$
With π k ( h ) $$ {\pi}_k^{(h)} $$ , τ i k ( h ) $$ {\tau}_{ik}^{(h)} $$ and β 0 ( h ) $$ {\beta}_0^{(h)} $$ fixed, we can in principle directly maximize the function identified in equation (14) over ϕ $$ \phi $$ . However, the function a ( y i j ( t ν ) , ϕ , ρ 0 ) $$ a\left({y}_{ij}\left({t}_{\nu}\right),\phi, {\rho}_0\right) $$ is cumbersome to compute directly, so we use the R package tweedie (Dunn and Smyth, 2005, 2008) to compute the distribution of Y $$ Y $$ identified in statement (2), and update ϕ $$ \phi $$ by letting ĉ i ( h ) = argmax k ∈ { 1 , … , K } τ i k ( h ) $$ {\hat{c}}_i^{(h)}={\mathrm{argmax}}_{k\in \left\{1,\dots, K\right\}}{\tau}_{ik}^{(h)} $$ and maximizing over the original log-likelihood function instead, i.e.,
ϕ ( h ) = argmax ϕ log ℙ ( D , ĉ ( h ) ; β 0 ( h ) , π ( h ) , ϕ ) . $$ {\phi}^{(h)}=\underset{\phi }{\mathrm{argmax}}\kern0.3em \log \mathbb{P}\left(D,{\hat{c}}^{(h)};{\beta}_0^{(h)},{\pi}^{(h)},\phi \right). $$ (15)
We do this directly using the R function optim (R Core Team, 2022).

4.2 Tuning parameter selection

We use leave-one-out cross-validation to choose the tuning parameters ξ 1 , … , ξ p $$ {\xi}_1,\dots, {\xi}_p $$ when fitting our model. In particular, each time we utilize observations made at T − 1 $$ T-1 $$ time points to train the model and then test the trained model on the observations made at the remaining time point. To avoid boundary effects, our leave-one-out procedure is repeated only T − 2 $$ T-2 $$ times (as opposed to the usual T $$ T $$ times), because we always retain the observations at times t 1 $$ {t}_1 $$ and t T $$ {t}_T $$ in the training set—only those at times t 2 , … , t T − 1 $$ {t}_2,\dots, {t}_{T-1} $$ are used (one at a time) as test points. In our implementation, the loss is defined as the negative log-likelihood of the fitted model, and the overall loss is taken as the average across the T − 2 $$ T-2 $$ repeats. We select the ξ $$ \xi $$ 's that give rise to the smallest loss.

5 Simulations

In this section, we report the results of simulation studies that demonstrate the performance of our restricted Tweedie SBM. In Section 5.1, we focus on the vanilla model alone; and in Section 5.2, we consider both fixed and time-varying covariate effects.

We mainly considered two aspects of the performance, the clustering quality and the accuracy of the estimated covariate effects. We measure the latter by the mean squared error and the former by a metric called “normalized mutual information” (NMI) (Danon et al., 2005). If C 1 $$ {C}_1 $$ and C 2 $$ {C}_2 $$ are the estimated and true community labels of the same set of N $$ N $$ nodes, the NMI is simply their mutual information normalized by the sum of their respective entropies, i.e.,
NMI ( C 1 , C 2 ) = 2 ∑ i = 1 K ∑ j = 1 K m i j N log ( m i j / N ) ( m i · / N ) ( m · j / N ) − ∑ i = 1 K m i · N log m i · N − ∑ j = 1 K m · j N log m · j N , $$ \mathrm{NMI}\left({C}_1,{C}_2\right)=\frac{2\sum \limits_{i=1}^K\sum \limits_{j=1}^K\frac{m_{ij}}{N}\log \frac{\left({m}_{ij}/N\right)}{\left({m}_{i\cdotp }/N\right)\left({m}_{\cdotp j}/N\right)}}{-\sum \limits_{i=1}^K\frac{m_{i\cdotp }}{N}\log \frac{m_{i\cdotp }}{N}-\sum \limits_{j=1}^K\frac{m_{\cdotp j}}{N}\log \frac{m_{\cdotp j}}{N}}, $$ (16)
where m i j $$ {m}_{ij} $$ is the number of nodes assigned to community i $$ i $$ by C 1 $$ {C}_1 $$ and simultaneously to community j $$ j $$ by C 2 $$ {C}_2 $$ , while m i · $$ {m}_{i\cdotp } $$ is the number of nodes assigned to community i $$ i $$ by C 1 $$ {C}_1 $$ regardless of their assignments by C 2 $$ {C}_2 $$ , and m · j $$ {m}_{\cdotp j} $$ the number of nodes assigned to community j $$ j $$ by C 2 $$ {C}_2 $$ regardless of their assignments by C 1 $$ {C}_1 $$ . The NMI ranges from 0 to 1, with values closer to 1 indicating better agreement between the estimated and true community labels.

For all simulations, we fixed the true number of communities to be K = 3 $$ K=3 $$ , with prior probabilities π = ( 0 . 2 , 0 . 3 , 0 . 5 ) $$ \pi =\left(0.2,0.3,0.5\right) $$ . For the true matrix β 0 $$ {\beta}_0 $$ , we set all diagonal entries β 0 k k $$ {\beta}_0^{kk} $$ to be equal, and all off-diagonal entries β 0 k ℓ $$ {\beta}_0^{k\mathit{\ell}} $$ to be equal as well—this way, the entire matrix is completely specified by just two numbers.

To avoid getting stuck at poor local optima, we used multiple initial values in each run.

5.1 Simulation from the vanilla model

First, we assessed the performance of our vanilla model (Section 2.2), and compared it with the Poisson SBM and spectral clustering. The Poisson SBM assumes the edges follow Poisson distributions; we simply rounded each y i j $$ {y}_{ij} $$ into an integer and fitted it using the function estimateSimpleSBM in the R package sbm (Chiquet et al., 2023, v0.4.5). To implement spectral clustering, we used the function reg.SSP from the R package randnet (Li et al., 2022, v0.5). The function estimateSimpleSBM uses results from a bipartite SBM as its initial values. To make a more informative comparison, we used two different initialization strategies to fit our model: (i) starting from 30 sets of randomly drawn community labels and picking the best solution afterward, and (ii) starting from the Poisson SBM result itself.

We generated Y $$ Y $$ using nine different combinations of ( ϕ , ρ ) $$ \left(\phi, \rho \right) $$ with ϕ = 0 . 5 , 1 , 2 $$ \phi =0.5,1,2 $$ and ρ = 1 . 2 , 1 . 5 , 1 . 8 $$ \rho =1.2,1.5,1.8 $$ , and three different matrices for β 0 $$ {\boldsymbol{\beta}}_0 $$ :
Scenario 1: ( β 0 k k , β 0 k ℓ ) = ( 1 . 0 , 0 . 0 ) ⇒ exp ( β 0 k k ) − exp ( β 0 k ℓ ) ≈ 1 . 72 ; Scenario 2: ( β 0 k k , β 0 k ℓ ) = ( 0 . 5 , − 0 . 5 ) ⇒ exp ( β 0 k k ) − exp ( β 0 k ℓ ) ≈ 1 . 04 ; Scenario 3: ( β 0 k k , β 0 k ℓ ) = ( 0 . 0 , − 1 . 0 ) ⇒ exp ( β 0 k k ) − exp ( β 0 k ℓ ) ≈ 0 . 63 . $$ {\displaystyle \begin{array}{ll}\hfill \mathrm{Scenario}\ 1:\kern0.3em \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(1.0,0.0\right)\Rightarrow & \exp \left({\beta}_0^{k k}\right)-\exp \left({\beta}_0^{k\mathit{\ell}}\right)\approx 1.72;\\ {}\hfill \mathrm{Scenario}\ 2:\kern0.3em \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.5,-0.5\right)\Rightarrow & \exp \left({\beta}_0^{k k}\right)-\exp \left({\beta}_0^{k\mathit{\ell}}\right)\approx 1.04;\\ {}\hfill \mathrm{Scenario}\ 3:\kern0.3em \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.0,-1.0\right)\Rightarrow & \exp \left({\beta}_0^{k k}\right)-\exp \left({\beta}_0^{k\mathit{\ell}}\right)\approx 0.63.\end{array}} $$

According to the discrepancy in μ i j $$ {\mu}_{ij} $$ between ( i , j ) $$ \left(i,j\right) $$ -pairs that belong to the same group and those that belong to different groups, the clustering difficulty of the three designs can be roughly ordered as Scenario 1 < $$ < $$ Scenario 2 < $$ < $$ Scenario 3.

Tables 1–3 summarize the averages and the standard errors of NMI for different methods over 50 simulation runs, respectively, for Scenarios 1–3. As expected, all methods perform the best in Scenario 1 and the worst in Scenario 3. Their performances improved as the sample size n $$ n $$ increased, or as the parameter ϕ $$ \phi $$ decreased; as the dispersion parameter, a smaller ϕ $$ \phi $$ means a reduced variance and an easier problem.

Table 1. Summary of the NMI in Scenario 1, ( β 0 k k , β 0 k ℓ ) = ( 1 , 0 ) $$ \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(1,0\right) $$ , over 50 simulation runs.
ϕ $$ \phi $$ ρ $$ \rho $$ n $$ n $$ Restricted Tweedie SBM Poisson Spectral
Random Init. Poisson Init. SBM Clustering
2 1.2 50 0.9097 (0.016) 0.8275 (0.023) 0.8099 (0.022) 0.5547 (0.012)
100 0.9958 (0.002) 0.9958 (0.002) 0.9950 (0.002) 0.9185 (0.019)
1.5 50 0.8647 (0.019) 0.7780 (0.020) 0.7275 (0.020) 0.5152 (0.012)
100 0.9878 (0.003) 0.9878 (0.003) 0.9865 (0.003) 0.7690 (0.025)
1.8 50 0.7644 (0.017) 0.7180 (0.020) 0.6539 (0.020) 0.4857 (0.015)
100 0.9828 (0.004) 0.9828 (0.004) 0.9826 (0.004) 0.6597 (0.015)
1 1.2 50 0.9918 (0.005) 0.9946 (0.004) 0.9880 (0.004) 0.7529 (0.027)
100 1 (0) 1 (0) 1 (0) 1 (0)
1.5 50 0.9778 (0.008) 0.9859 (0.006) 0.9745 (0.008) 0.7034 (0.023)
100 1 (0) 1 (0) 1 (0) 0.9991 (0.001)
1.8 50 0.9653 (0.010) 0.9644 (0.010) 0.9512 (0.012) 0.6702 (0.019)
100 0.9992 (0.001) 0.9992 (0.001) 0.9992 (0.001) 0.9656 (0.013)
0.5 1.2 50 1 (0) 1 (0) 1 (0) 0.9934 (0.007)
100 1 (0) 1 (0) 1 (0) 1 (0)
1.5 50 1 (0) 1 (0) 1 (0) 0.9297 (0.019)
100 1 (0) 1 (0) 1 (0) 1 (0)
1.8 50 1 (0) 1 (0) 0.9985 (0.001) 0.8307 (0.025)
100 1 (0) 1 (0) 1 (0) 1 (0)
Table 2. Summary of NMI in Scenario 2, ( β 0 k k , β 0 k ℓ ) = ( 0 . 5 , − 0 . 5 ) $$ \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.5,-0.5\right) $$ , over 50 runs. A superscript “ † $$ \dagger $$ ” denotes a case in which (restricted Tweedie SBM with random initialization) < $$ < $$ (Poisson SBM) ≤ $$ \le $$ (restricted Tweedie SBM with Poisson initialization) in their respective clustering performances.
ϕ $$ \phi $$ ρ $$ \rho $$ n $$ n $$ Restricted Tweedie SBM Poisson Spectral
Random Init. Poisson Init. SBM Clustering
2 1.2 50 0.7490 (0.023) 0.6713 (0.024) 0.640 (0.021) 0.4515 (0.014)
100 0.9698 (0.007) 0.9592 (0.011) 0.9603 (0.011) 0.6936 (0.023)
1.5 50 0.6921 (0.023) 0.6327 (0.021) 0.6031 (0.021) 0.4596 (0.018)
100 0.9568 (0.009) 0.9650 (0.007) 0.9430 (0.011) 0.6133 (0.014)
1.8 50 0.7052 (0.022) 0.6315 (0.023) 0.5727 (0.020) 0.4174 (0.020)
100 0.9803 (0.004) 0.9539 (0.013) 0.9362 (0.013) 0.6433 (0.012)
1 1.2 50 0.9490 (0.013) 0.9284 (0.014) 0.9037 (0.013) 0.6489 (0.021)
100 0.9992 (0.001) 0.9992 (0.001) 0.9984 (0.001) 0.9918 (0.003)
1.5 50 0.9330 (0.014) 0.9193 (0.014) 0.9127 (0.014) 0.6304 (0.018)
100 1 (0) 1 (0) 0.9976 (0.001) 0.9926 (0.003)
1.8 50 0.9288 (0.013) 0.9235 (0.014) 0.9103 (0.014) 0.6437 (0.015)
100 0.9992 (0.001) 0.9992 (0.001) 0.9967 (0.002) 0.9375 (0.017)
0.5 1.2 50 † $$ {}^{\dagger } $$ 0.9961 (0.004) 1 (0) 1 (0) 0.8504 (0.027)
100 1 (0) 1 (0) 1 (0) 0.9991 (0.001)
1.5 50 † $$ {}^{\dagger } $$ 0.9847 (0.009) 1 (0) 1 (0) 0.8193 (0.026)
100 1 (0) 1 (0) 1 (0) 1 (0)
1.8 50 † $$ {}^{\dagger } $$ 0.9879 (0.007) 1 (0) 0.9973 (0.002) 0.7947 (0.026)
100 1 (0) 1 (0) 1 (0) 1 (0)
Table 3. Summary of NMI in Scenario 3, ( β 0 k k , β 0 k ℓ ) = ( 0 , − 1 ) $$ \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0,-1\right) $$ , over 50 simulation runs. A superscript “ † $$ \dagger $$ ” denotes a case in which (restricted Tweedie SBM with random initialization) < $$ < $$ (Poisson SBM) ≤ $$ \le $$ (restricted Tweedie SBM with Poisson initialization) in their respective clustering performances.
ϕ $$ \phi $$ ρ $$ \rho $$ n $$ n $$ Restricted Tweedie SBM Poisson Spectral
Random Init. Poisson Init. SBM Clustering
2 1.2 50 0.4385 (0.032) 0.4340 (0.027) 0.4243 (0.025) 0.2889 (0.022)
100 0.8497 (0.013) 0.8025 (0.019) 0.774 (0.020) 0.5134 (0.016)
1.5 50 0.5611 (0.023) 0.5226 (0.023) 0.5071 (0.022) 0.3462 (0.018)
100 0.9097 (0.012) 0.8606 (0.016) 0.8146 (0.017) 0.5737 (0.012)
1.8 50 0.6179 (0.022) 0.5771 (0.024) 0.522 (0.021) 0.4102 (0.018)
100 0.9567 (0.009) 0.8736 (0.020) 0.8377 (0.020) 0.5985 (0.013)
1 1.2 50 0.8710 (0.016) 0.7404 (0.017) 0.7325 (0.016) 0.5379 (0.011)
100 0.9893 (0.006) 0.9967 (0.002) 0.9842 (0.003) 0.862 (0.022)
1.5 50 0.8709 (0.016) 0.7763 (0.017) 0.7684 (0.016) 0.5601 (0.012)
100 0.9950 (0.004) 0.9992 (0.001) 0.9876 (0.003) 0.8311 (0.022)
1.8 50 0.8806 (0.017) 0.8039 (0.019) 0.7901 (0.018) 0.6092 (0.013)
100 0.9992 (0.001) 0.9992 (0.001) 0.9934 (0.002) 0.8876 (0.022)
0.5 1.2 50 0.9414 (0.014) 0.8998 (0.017) 0.8817 (0.016) 0.7379 (0.028)
100 † $$ {}^{\dagger } $$ 0.9956 (0.004) 1 (0) 1 (0) 0.9983 (0.001)
1.5 50 0.9591 (0.012) 0.9112 (0.015) 0.8999 (0.015) 0.7354 (0.026)
100 1 (0) 1 (0) 1 (0) 1 (0)
1.8 50 1 (0) 0.9727 (0.01) 0.9550 (0.01) 0.7549 (0.022)
100 1 (0) 1 (0) 1 (0) 1 (0)

Overall, our restricted Tweedie SBM and the Poisson SBM tended to outperform spectral clustering. Among all 54 sets of simulation results, our model with a random initialization compares favourably with other methods in 50 out of 54 cases. In the remaining four sets (marked by a superscript “ † $$ \dagger $$ ” in the tables), the Poisson SBM was slightly better. But our method could still be superior to the Poisson SBM in these four sets if we had initialized our algorithm with the estimates from the Poisson SBM. It is evident that in all cases our restricted Tweedie SBM can further improve the clustering result of the Poisson SBM.

5.2 Simulation from a model with covariates

We now study the more general version of our model which includes both time-fixed ( β $$ \boldsymbol{\beta} $$ ) and time-varying ( β ( t ) $$ \boldsymbol{\beta} (t) $$ ) coefficients:
y i j ( t ) ∼ Tw ( μ i j ( t ) , ϕ , ρ ) , 1 < ρ < 2 , where log ( μ i j ( t ) ) = β 0 k ℓ + w i j ⊤ β + x i j ⊤ β ( t ) , if c i = k and c j = ℓ . $$ {\displaystyle \begin{array}{ll}\hfill & {y}_{ij}(t)\sim \mathrm{Tw}\left({\mu}_{ij}(t),\phi, \rho \right),\kern1em 1<\rho <2,\\ {}\hfill \mathrm{where}\kern0.3em & \log \left({\mu}_{ij}(t)\right)={\beta}_0^{k\mathit{\ell}}+{\boldsymbol{w}}_{ij}^{\top}\boldsymbol{\beta} +{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} (t),\kern0.3em \mathrm{if}\kern0.3em {c}_i=k\kern0.3em \mathrm{and}\kern0.3em {c}_j=\ell .\end{array}} $$
We fixed the parameter ρ $$ \rho $$ at 1.5, as it represents a moderate value in our restricted range of ( 1 , 2 ) $$ \left(1,2\right) $$ , and explored two different values for the parameter ϕ $$ \phi $$ : ϕ = 1 $$ \phi =1 $$ and ϕ = 2 $$ \phi =2 $$ . We used two scenarios for the true matrix β 0 $$ {\beta}_0 $$ :
Scenario 4: ( β 0 k k , β 0 k ℓ ) = ( 0 . 25 , − 0 . 25 ) ⇒ exp ( β 0 k k ) − exp ( β 0 k ℓ ) ≈ 0 . 51 ; Scenario 5: ( β 0 k k , β 0 k ℓ ) = ( 0 . 15 , − 0 . 15 ) ⇒ exp ( β 0 k k ) − exp ( β 0 k ℓ ) ≈ 0 . 30 . $$ {\displaystyle \begin{array}{ll}\hfill \mathrm{Scenario}\ 4:\kern0.3em \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.25,-0.25\right)\Rightarrow & \exp \left({\beta}_0^{k k}\right)-\exp \left({\beta}_0^{k\mathit{\ell}}\right)\approx 0.51;\\ {}\hfill \mathrm{Scenario}\ 5:\kern0.3em \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.15,-0.15\right)\Rightarrow & \exp \left({\beta}_0^{k k}\right)-\exp \left({\beta}_0^{k\mathit{\ell}}\right)\approx 0.30.\end{array}} $$
These are similar to the earlier Scenarios 1, 2 and 3, but even more difficult to cluster.

We considered 20 time-fixed covariates w i j ∈ ℝ 20 $$ {\boldsymbol{w}}_{ij}\in {\mathbb{R}}^{20} $$ and 5 time-varying covariates x i j ∈ ℝ 5 $$ {\boldsymbol{x}}_{ij}\in {\mathbb{R}}^5 $$ , all independently generated from the uniform distribution on ( − 1 , 1 ) $$ \left(-1,1\right) $$ . The true time-fixed covariate effect β $$ \boldsymbol{\beta} $$ consisted of 20 equally spaced values ranging from −1 to 1. The five true time-varying coefficients β ( t ) $$ \boldsymbol{\beta} (t) $$ were specified as: β 1 ( t ) = 2 t − 1 $$ {\beta}_1(t)=2t-1 $$ , β 2 ( t ) = sin ( 2 π t ) + 1 $$ {\beta}_2(t)=\sin \left(2\pi t\right)+1 $$ , β 3 ( t ) = − 17 ( t − 0 . 1 ) ( t − 0 . 5 ) ( t − 0 . 8 ) + 0 . 5 $$ {\beta}_3(t)=-17\left(t-0.1\right)\left(t-0.5\right)\left(t-0.8\right)+0.5 $$ , β 4 ( t ) = cos ( 4 π t ) $$ {\beta}_4(t)=\cos \left(4\pi t\right) $$ , and β 5 ( t ) = − 1 + 2 exp ( − 3 t ) $$ {\beta}_5(t)=-1+2\exp \left(-3t\right) $$ . Finally, the datasets were simulated in such a way that the network was observed at T = 20 $$ T=20 $$ equally spaced time points on [ 0 , 1 ] $$ \left[0,1\right] $$ .

We used 10 different sets of initial values for each simulation run. To evaluate the performance of the estimated β ^ $$ \hat{\boldsymbol{\beta}} $$ , we calculated the overall mean squared error as
Err ( β ^ ) = 1 20 ∑ j = 1 20 ( β ^ j − β j ) 2 . $$ \mathrm{Err}\left(\hat{\boldsymbol{\beta}}\right)=\frac{1}{20}\sum \limits_{j=1}^{20}{\left({\hat{\boldsymbol{\beta}}}_j-{\boldsymbol{\beta}}_j\right)}^2. $$ (17)
To evaluate the performance of the estimated time-varying coefficients β ^ j ( t ) $$ {\hat{\beta}}_j(t) $$ for each of j ∈ { 1 , … , 5 } $$ j\in \left\{1,\dots, 5\right\} $$ , we approximated the estimation error:
Err ( β ^ j ( t ) ) = ∫ 0 1 [ β ^ j ( t ) − β j ( t ) ] 2 d t , $$ \mathrm{Err}\left({\hat{\beta}}_j(t)\right)={\int}_0^1{\left[{\hat{\beta}}_j(t)-{\beta}_j(t)\right]}^2 dt, $$
with a Riemann sum over a finite set of time points.

In general, the tuning parameters ξ 1 , … , ξ 5 $$ {\xi}_1,\dots, {\xi}_5 $$ are to be selected by cross-validation. To reduce the computational cost, here we simply fixed all of them at ξ = 0 . 5 $$ \xi =0.5 $$ . The Supplementary Material contains a small sensitivity study using ξ = 0 . 1 < 0 . 5 $$ \xi =0.1<0.5 $$ and ξ = 1 . 0 > 0 . 5 $$ \xi =1.0>0.5 $$ , from which one can see that the clustering performance is minimally affected by the choice of ξ $$ \xi $$ , but larger ξ $$ \xi $$ values lead to smoother estimates of β ( t ) $$ \boldsymbol{\beta} (t) $$ . We can also see that the optimal tuning parameter is not the same for each function. Most notably, the function β 4 ( t ) $$ {\beta}_4(t) $$ has a substantially larger total variation than the other four functions, and would require a smaller tuning parameter as a result. The inclusion of such a function in our simulation study has indeed been deliberate, so that we can highlight this important point.

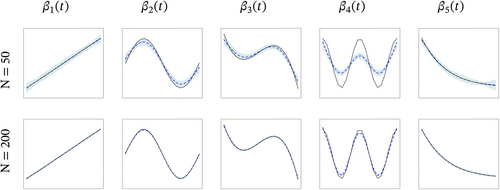
For all simulated cases with different combinations of β 0 $$ {\beta}_0 $$ and ϕ $$ \phi $$ , Table 4 summarizes the metrics, NMI, Err ( β ^ ) $$ \mathrm{Err}\left(\hat{\boldsymbol{\beta}}\right) $$ and Err ( β ^ j ( t ) ) $$ \mathrm{Err}\left({\hat{\beta}}_j(t)\right) $$ , for j ∈ { 1 , … , 5 } $$ j\in \left\{1,\dots, 5\right\} $$ , across 50 repeated simulation runs. Figure 2 shows visually how well the time-varying coefficients were estimated for Scenario 5 with ϕ = 2 $$ \phi =2 $$ , the most challenging case in our entire simulation study. In particular, the pointwise mean and five times the standard deviation of each β ^ j ( t ) $$ {\hat{\beta}}_j(t) $$ are plotted, for n = 50 $$ n=50 $$ and 200. Similar plots for Scenario 4 and Scenario 5 with ϕ = 1 $$ \phi =1 $$ are included in the Supplementary Material. From these plots, as well as from Table 4 itself, it is quite clear that the estimation performance of covariate effects across different scenarios is largely unaffected by the varying levels of clustering difficulty, as foreshadowed by Theorem 1. Finally, we also report computational times in the Supplementary Material for all simulation scenarios.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Visualizing the estimation performance of the time-varying coefficients in Scenario 5 with ϕ = 2 $$ \phi =2 $$ , using a fixed tuning parameter of ξ = 0 . 5 $$ \xi =0.5 $$ . The black solid line represents the true function of β j ( t ) $$ {\beta}_j(t) $$ ; the blue dashed line shows the pointwise mean of the estimated β ^ j ( t ) $$ {\hat{\beta}}_j(t) $$ over 50 simulation runs; and the light blue shading captures the pointwise confidence band of plus and minus five times the standard deviation.
Table 4. Summary of clustering and estimation performance (using ξ = 0 . 5 $$ \xi =0.5 $$ ) from a model with covariates over 50 simulation runs, with ρ = 1 . 5 $$ \rho =1.5 $$ .
Scenario 4: ( β 0 k k , β 0 k ℓ ) = ( 0 . 25 , − 0 . 25 ) $$ \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.25,-0.25\right) $$
( ϕ , n ) $$ \left(\phi, n\right) $$ ( 1 , 50 ) $$ \left(1,50\right) $$ ( 1 , 200 ) $$ \left(1,200\right) $$ ( 2 , 50 ) $$ \left(2,50\right) $$ ( 2 , 200 ) $$ \left(2,200\right) $$
NMI 1 1 1 1
(0) (0) (0) (0)
Err( β ^ $$ \hat{\boldsymbol{\beta}} $$ ) 3 . 8 × 1 0 − 4 $$ 3.8\times 1{0}^{-4} $$ 1 . 9 × 1 0 − 5 $$ 1.9\times 1{0}^{-5} $$ 4.7 × 10 − 4 $$ 4.7\times {10}^{-4} $$ 2 . 5 × 1 0 − 5 $$ 2.5\times 1{0}^{-5} $$
( 1 . 4 × 1 0 − 5 $$ 1.4\times 1{0}^{-5} $$ ) ( 7 . 1 × 1 0 − 7 $$ 7.1\times 1{0}^{-7} $$ ) ( 1 . 9 × 1 0 − 5 $$ 1.9\times 1{0}^{-5} $$ ) ( 1 . 0 × 1 0 − 6 $$ 1.0\times 1{0}^{-6} $$ )
Err( β ^ 1 ( t ) $$ {\hat{\beta}}_1(t) $$ ) 4.7 × 10 − 4 $$ 4.7\times {10}^{-4} $$ 4 . 6 × 1 0 − 5 $$ 4.6\times 1{0}^{-5} $$ 8.9 × 10 − 4 $$ 8.9\times {10}^{-4} $$ 1.0 × 10 − 4 $$ 1.0\times {10}^{-4} $$
( 3 . 5 × 1 0 − 5 $$ 3.5\times 1{0}^{-5} $$ ) 3 . 9 × 1 0 − 6 $$ 3.9\times 1{0}^{-6} $$ ) ( 8 . 1 × 1 0 − 5 $$ 8.1\times 1{0}^{-5} $$ ) ( 6 . 7 × 1 0 − 6 $$ 6.7\times 1{0}^{-6} $$ )
Err( β ^ 2 ( t ) $$ {\hat{\beta}}_2(t) $$ ) 1.2 × 10 − 2 $$ 1.2\times {10}^{-2} $$ 1.5 × 10 − 4 $$ 1.5\times {10}^{-4} $$ 1.2 × 10 − 2 $$ 1.2\times {10}^{-2} $$ 1.8 × 10 − 4 $$ 1.8\times {10}^{-4} $$
( 2.1 × 10 − 4 $$ 2.1\times {10}^{-4} $$ ) ( 7 . 5 × 1 0 − 6 $$ 7.5\times 1{0}^{-6} $$ ) ( 3.5 × 10 − 4 $$ 3.5\times {10}^{-4} $$ ) ( 1 . 1 × 1 0 − 5 $$ 1.1\times 1{0}^{-5} $$ )
Err( β ^ 3 ( t ) $$ {\hat{\beta}}_3(t) $$ ) 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ 4.1 × 10 − 4 $$ 4.1\times {10}^{-4} $$ 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ 4.6 × 10 − 4 $$ 4.6\times {10}^{-4} $$
( 2.4 × 10 − 4 $$ 2.4\times {10}^{-4} $$ ) ( 8 . 0 × 1 0 − 6 $$ 8.0\times 1{0}^{-6} $$ ) ( 2.9 × 10 − 4 $$ 2.9\times {10}^{-4} $$ ) ( 1 . 6 × 1 0 − 5 $$ 1.6\times 1{0}^{-5} $$ )
Err( β ^ 4 ( t ) $$ {\hat{\beta}}_4(t) $$ ) 1.6 × 10 − 1 $$ 1.6\times {10}^{-1} $$ 8.3 × 10 − 3 $$ 8.3\times {10}^{-3} $$ 1.5 × 10 − 1 $$ 1.5\times {10}^{-1} $$ 8.4 × 10 − 3 $$ 8.4\times {10}^{-3} $$
( 5.1 × 10 − 4 $$ 5.1\times {10}^{-4} $$ ) ( 4 . 3 × 1 0 − 5 $$ 4.3\times 1{0}^{-5} $$ ) ( 5.9 × 10 − 4 $$ 5.9\times {10}^{-4} $$ ) ( 6 . 5 × 1 0 − 5 $$ 6.5\times 1{0}^{-5} $$ )
Err( β ^ 5 ( t ) $$ {\hat{\beta}}_5(t) $$ ) 6.6 × 10 − 4 $$ 6.6\times {10}^{-4} $$ 6 . 3 × 1 0 − 5 $$ 6.3\times 1{0}^{-5} $$ 1.1 × 10 − 3 $$ 1.1\times {10}^{-3} $$ 1.1 × 10 − 4 $$ 1.1\times {10}^{-4} $$
( 4 . 8 × 1 0 − 5 $$ 4.8\times 1{0}^{-5} $$ ) ( 3 . 9 × 1 0 − 6 $$ 3.9\times 1{0}^{-6} $$ ) ( 1.0 × 10 − 4 $$ 1.0\times {10}^{-4} $$ ) ( 7 . 4 × 1 0 − 6 $$ 7.4\times 1{0}^{-6} $$ )
Scenario 5: ( β 0 k k , β 0 k ℓ ) = ( 0 . 15 , − 0 . 15 ) $$ \left({\beta}_0^{k k},{\beta}_0^{k\mathit{\ell}}\right)=\left(0.15,-0.15\right) $$
( ϕ , n ) $$ \left(\phi, n\right) $$ ( 1 , 50 ) $$ \left(1,50\right) $$ ( 1 , 200 ) $$ \left(1,200\right) $$ ( 2 , 50 ) $$ \left(2,50\right) $$ ( 2 , 200 ) $$ \left(2,200\right) $$
NMI 9.7 × 10 − 1 $$ 9.7\times {10}^{-1} $$ 1 9.6 × 10 − 1 $$ 9.6\times {10}^{-1} $$ 1
( 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ ) (0) ( 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ ) (0)
Err( β ^ $$ \hat{\boldsymbol{\beta}} $$ ) 2.2 × 10 − 4 $$ 2.2\times {10}^{-4} $$ 1 . 0 × 1 0 − 5 $$ 1.0\times 1{0}^{-5} $$ 3.1 × 10 − 4 $$ 3.1\times {10}^{-4} $$ 1 . 7 × 1 0 − 5 $$ 1.7\times 1{0}^{-5} $$
( 7 . 6 × 1 0 − 6 $$ 7.6\times 1{0}^{-6} $$ ) ( 5 . 0 × 1 0 − 7 $$ 5.0\times 1{0}^{-7} $$ ) ( 1 . 1 × 1 0 − 5 $$ 1.1\times 1{0}^{-5} $$ ) ( 7 . 1 × 1 0 − 7 $$ 7.1\times 1{0}^{-7} $$ )
Err( β ^ 1 ( t ) $$ {\hat{\beta}}_1(t) $$ ) 4.3 × 10 − 4 $$ 4.3\times {10}^{-4} $$ 4 . 7 × 1 0 − 5 $$ 4.7\times 1{0}^{-5} $$ 8.2 × 10 − 4 $$ 8.2\times {10}^{-4} $$ 8 . 6 × 1 0 − 5 $$ 8.6\times 1{0}^{-5} $$
( 3 . 4 × 1 0 − 5 $$ 3.4\times 1{0}^{-5} $$ ) ( 3 . 8 × 1 0 − 6 $$ 3.8\times 1{0}^{-6} $$ ) ( 7 . 0 × 1 0 − 5 $$ 7.0\times 1{0}^{-5} $$ ) ( 6 . 0 × 1 0 − 6 $$ 6.0\times 1{0}^{-6} $$ )
Err( β ^ 2 ( t ) $$ {\hat{\beta}}_2(t) $$ ) 1.2 × 10 − 2 $$ 1.2\times {10}^{-2} $$ 1.2 × 10 − 4 $$ 1.2\times {10}^{-4} $$ 1.2 × 10 − 2 $$ 1.2\times {10}^{-2} $$ 1.7 × 10 − 4 $$ 1.7\times {10}^{-4} $$
( 2.3 × 10 − 4 $$ 2.3\times {10}^{-4} $$ ) ( 5 . 3 × 1 0 − 6 $$ 5.3\times 1{0}^{-6} $$ ) ( 3.7 × 10 − 4 $$ 3.7\times {10}^{-4} $$ ) ( 9 . 2 × 1 0 − 6 $$ 9.2\times 1{0}^{-6} $$ )
Err( β ^ 3 ( t ) $$ {\hat{\beta}}_3(t) $$ ) 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ 4.0 × 10 − 4 $$ 4.0\times {10}^{-4} $$ 1.1 × 10 − 2 $$ 1.1\times {10}^{-2} $$ 4.3 × 10 − 4 $$ 4.3\times {10}^{-4} $$
( 2.0 × 10 − 4 $$ 2.0\times {10}^{-4} $$ ) ( 1 . 1 × 1 0 − 5 $$ 1.1\times 1{0}^{-5} $$ ) ( 2.9 × 10 − 4 $$ 2.9\times {10}^{-4} $$ ) ( 1 . 2 × 1 0 − 5 $$ 1.2\times 1{0}^{-5} $$ )
Err( β ^ 4 ( t ) $$ {\hat{\beta}}_4(t) $$ ) 1.5 × 10 − 1 $$ 1.5\times {10}^{-1} $$ 8.3 × 10 − 3 $$ 8.3\times {10}^{-3} $$ 1.5 × 10 − 1 $$ 1.5\times {10}^{-1} $$ 8.3 × 10 − 3 $$ 8.3\times {10}^{-3} $$
( 5.0 × 10 − 4 $$ 5.0\times {10}^{-4} $$ ) ( 4 . 4 × 1 0 − 5 $$ 4.4\times 1{0}^{-5} $$ ) ( 6.3 × 10 − 4 $$ 6.3\times {10}^{-4} $$ ) ( 6 . 2 × 1 0 − 5 $$ 6.2\times 1{0}^{-5} $$ )
Err( β ^ 5 ( t ) $$ {\hat{\beta}}_5(t) $$ ) 7.4 × 10 − 4 $$ 7.4\times {10}^{-4} $$ 6 . 5 × 1 0 − 5 $$ 6.5\times 1{0}^{-5} $$ 9.9 × 10 − 4 $$ 9.9\times {10}^{-4} $$ 1.1 × 10 − 4 $$ 1.1\times {10}^{-4} $$
( 4 . 6 × 1 0 − 5 $$ 4.6\times 1{0}^{-5} $$ ) ( 3 . 9 × 1 0 − 6 $$ 3.9\times 1{0}^{-6} $$ ) ( 8 . 0 × 1 0 − 5 $$ 8.0\times 1{0}^{-5} $$ ) ( 7 . 0 × 1 0 − 6 $$ 7.0\times 1{0}^{-6} $$ )

6 An application: International trading

In this section, we apply the restricted Tweedie SBM to study international trading relationships among different countries and how these relationships are influenced by geographical distances. As an example, we focus on the trading of apples—not only are these data readily available from the World Bank (World Integrated Trade Solution, 2023), but one can also surmise a priori that geographical distances will likely have a substantial impact on the trading due to the weight and perishable nature of this product.

From the international trading datasets provided by the World Bank (World Integrated Trade Solution, 2023), we have collected annual import and export values of edible and fresh apples among n = 66 $$ n=66 $$ countries from t 1 = 2002 $$ {t}_1=2002 $$ to t 20 = 2021 $$ {t}_{20}=2021 $$ . In each given year t ν $$ {t}_{\nu } $$ , we observe a 66-by-66 matrix Y ( t ν ) $$ Y\left({t}_{\nu}\right) $$ where each cell y i j ( t ν ) $$ {y}_{ij}\left({t}_{\nu}\right) $$ represents the trading value from country i $$ i $$ to country j $$ j $$ in thousands of US dollars during that year. We then average Y ( t ν ) $$ Y\left({t}_{\nu}\right) $$ with its transpose to ensure symmetry. Finally, a small number of entries with values ranging from 0 to 1 (i.e., total trading values less than $1,000) are thresholded to 0, and the remaining entries are logarithmically transformed. For the covariate x i j $$ {x}_{ij} $$ , we use the shortest geographical distance between the two trading countries based on their borders, which we calculate using R packages maps (code by Becker et al., 2022, v3.4.1) and geosphere (Hijmans, 2022, v1.5–18).

We employ the cross-validation procedure outlined in Section 4.2 to choose the tuning parameter ξ $$ \xi $$ . Figure 3 displays the CV error, showing the optimal tuning parameter to be ξ ∗ = 0 . 1 $$ {\xi}^{\ast }=0.1 $$ .

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Cross-validation errors change across a range of plausible values for the tuning parameter ξ $$ \xi $$ .

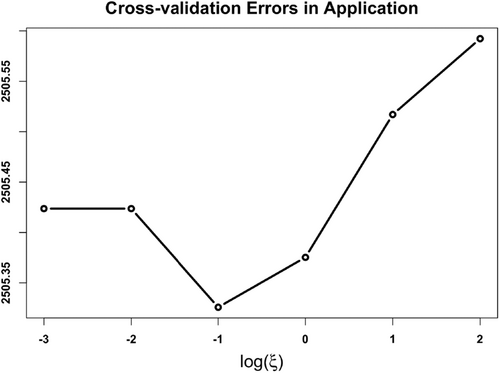
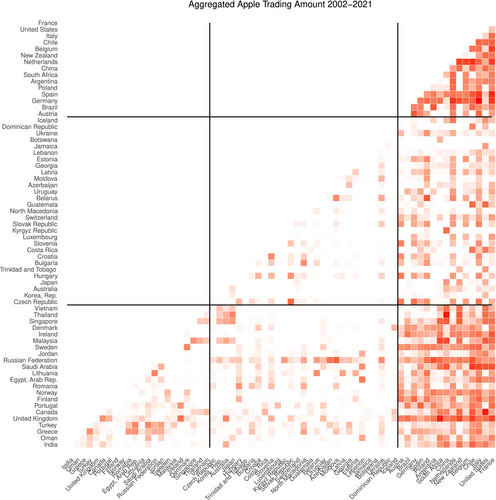
Table 5 shows how the 66 countries are clustered into three communities by our method. Figure 4 displays the aggregated matrix, Y ( 2002 ) + Y ( 2003 ) + ⋯ + Y ( 2021 ) $$ Y(2002)+Y(2003)+\cdots +Y(2021) $$ , with rows and columns having been permuted according to the inferred community labels. Clearly, countries in the first community trade intensively with each other and with countries in the third community. While both the second and third communities consist of countries that mainly trade with countries in the first community (rather than among themselves or between each other), the trading intensity with the first community is much higher for the third community than it is for the second.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The (aggregated) matrix, Y ( 2002 ) + ⋯ + Y ( 2021 ) $$ Y(2002)+\cdots +Y(2021) $$ , with rows and columns having been permuted according to the inferred community labels. Due to symmetry, only the lower half of the matrix is shown, with colour shadings being proportional to each entry's respective magnitude.
Table 5. Community detection results of 66 countries with K = 3 $$ K=3 $$ .
Community Countries
1 France, United States, Italy, Chile, Belgium, New Zealand, Netherlands, China, South Africa, Argentina, Poland, Spain, Germany, Brazil, Austria
2 Iceland, Dominican Republic, Ukraine, Botswana, Jamaica, Lebanon, Estonia, Georgia, Latvia, Moldova, Azerbaijan, Uruguay, Belarus, Guatemala, North Macedonia, Switzerland, Slovak Republic, Kyrgyz Republic, Luxembourg, Slovenia, Costa Rica, Croatia, Bulgaria, Trinidad and Tobago, Hungary, Japan, Australia, Korea Rep., Czech Republic
3 Vietnam, Thailand, Singapore, Denmark, Ireland, Malaysia, Sweden, Jordan, Russian Federation, Saudi Arabia, Lithuania, Egypt Arab Rep., Romania, Norway, Finland, Portugal, Canada, United Kingdom, Turkey, Greece, Oman, India

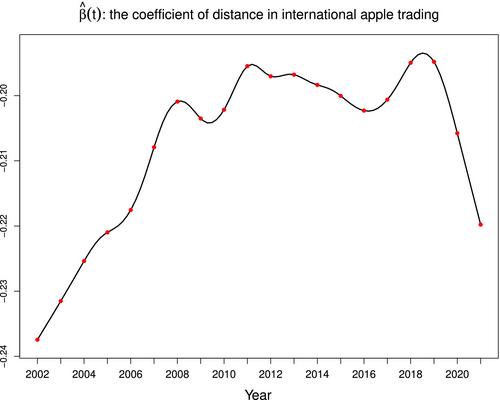
Figure 5 displays β ^ ( t ) $$ \hat{\beta}(t) $$ , the estimated effect of geographical distances on apple trading over time. We can make three pertinent observations. First, β ^ ( t ) $$ \hat{\beta}(t) $$ is negative during the entire study period—not surprising since longer distances can only increase the cost and the duration of transportation, and negatively impact fresh apple trading. Next, the magnitude of β ^ ( t ) $$ \hat{\beta}(t) $$ shows a generally decreasing trend over the twenty-year period of observation, implying that the negative effect of geographical distances is diminishing. This may be attributed to more efficient transportation methods and a reduced cost of shipment with time. Finally, two relatively big “dips” in β ^ ( t ) $$ \hat{\beta}(t) $$ are clearly visible—one after the financial crisis in 2008, and another after the onset of the COVID-19 pandemic in 2020.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Estimated covariate coefficient β ^ ( t ) $$ \hat{\beta}(t) $$ for ξ ∗ = 0 . 1 $$ {\xi}^{\ast }=0.1 $$ .

As we stated earlier in Section 2.2, methodologically we do not focus on the choice of K $$ K $$ in this paper. Instead, we include in the Supplementary Material some additional clustering results for these data using K = 5 $$ K=5 $$ and K = 9 $$ K=9 $$ , so as to provide some additional insights on the effect of varying K $$ K $$ . One key message of our paper has been that the functional estimate, β ^ ( t ) $$ \hat{\beta}(t) $$ , is unaffected by the community structure or the choice of K $$ K $$ , and indeed this is the case. For these data from 2002 to 2021, K = 9 $$ K=9 $$ appears to be “a maximum possible choice”, as an empty community occurs if K = 10 $$ K=10 $$ is chosen. The additional clustering results in the Supplementary Material indicate that, as K $$ K $$ increases, more detailed patterns start to emerge. For instance, two groups of countries—(Germany, Spain, China, Netherlands, Belgium, Italy, United States, France) and (Brazil, Argentina, South Africa, New Zealand, Chile)—are consistently clustered together whether K = 3 $$ K=3 $$ , 5, or 9. These countries are all active in apple trading. When K = 3 $$ K=3 $$ , they are clustered into a single community, but at K = 5 $$ K=5 $$ and K = 9 $$ K=9 $$ , they divide into two distinct communities. The latter group trades intensively with specific partners, while the former group trades broadly with nearly all countries. Therefore, at the lower value of K = 3 $$ K=3 $$ , general trading patterns are already detectable, whereas at larger values of K = 5 , 9 $$ K=5,9 $$ , more nuanced differences in trading behaviours are uncovered. As is often the case, there is not one “right” answer for these type of problems, and we can gain different insights by adopting various answers.

7 Discussion

In this paper, we have presented an extension of the classical SBM to address several critical challenges. Our main contributions can be summarized as follows.

First, we replaced the Bernoulli distribution with the restricted Tweedie distribution, allowing us to model nonnegative zero-inflated edge weights. This represents a significant improvement over traditional community detection approaches and addresses a previously unmet need in the existing literature for handling such network data. Moreover, this advancement is poised to have even broader applications, particularly in the analysis of financial-related network data.

Second, our methods further incorporate dynamic effects of nodal information, making them suitable for a wide range of real-world applications and providing a new mechanism for explaining the dynamics of network formation via the effect of covariates.

One of the most striking findings of our research is that, in the limit as the number of nodes approaches infinity, estimating the covariate coefficients becomes asymptotically independent of the community labels when maximizing the likelihood function. This insight has led to the development of an efficient two-step algorithm, enhancing the practicality of our framework.

The application of our model to an international trading network, focusing on the dynamic effects of geographic distance between countries, has provided valuable insights into the complexities of global economic relationships. Additionally, our simulation studies have demonstrated good clustering performance of our proposed framework, further highlighting its effectiveness in capturing hidden patterns within networks. In terms of theoretical contributions, our main focus is on showing that the profile likelihood specified in expression (9) is asymptotically independent of the initial community assignment, as established by Theorem 1. But as pointed out by one referee, it is desirable to investigate asymptotic properties such as consistency and the convergence rate of the proposed estimator. However, these are challenging problems for the following reasons. Our target is to maximize the log-likelihood function given in equation (8). As indicated in statement (12), ideally we want to maximize the marginal distribution of D $$ D $$ over a proper parameter space if we are able to compute the summation of the log-likelihood function over all possible configurations of c $$ c $$ . To deal with the infinite-dimensional objects β ( t ) $$ \beta (t) $$ in this setting, we may consider using the sieve estimation method to approximate each β ( t ) $$ \beta (t) $$ with proper basis functions. Then this problem can be formulated as a standard M $$ M $$ -estimation problem. Theoretical analysis of the large-sample properties of the estimator entails a quantification of the complexity of the sieve space. However, it should be noted that this procedure is not feasible as it is quite challenging to compute the summation over K n $$ {K}^n $$ terms for a large n $$ n $$ . Thus, we have to resort to variational inference to restrict the joint distribution of c $$ c $$ to a tractable family. Then we apply the EM algorithm to deal with the latent variable c $$ c $$ under this tractable setting. This treatment renders theoretical analysis of the asymptotic properties much more difficult, since it is no longer a standard M $$ M $$ -estimation problem. Thus, we will leave this to future work.

While our framework demonstrates its effectiveness, in practice community labels themselves may also evolve over time, which presents a promising avenue for future research. Extending our model to accommodate time-varying community labels, as demonstrated in works such as Xu and Hero (2014) and Matias and Miele (2017) where Markov chains are employed, is a straightforward next step. However, it is crucial to address the identifiability issues associated with these parameters, which will undoubtedly be a key focus of further exploration.

In conclusion, our work extends the classic SBM framework to better model nonnegative zero-inflated edge weights and analyze complex networks with dynamic nodal information. We believe that the methodologies presented here will inspire future research in the field of network analysis, opening doors to new insights and applications across various domains.

Data sharing

The R code used for conducting the simulation studies and for analyzing the trading dataset is available at https://github.com/JieJJian/TweedieSBM. The trading dataset itself can be downloaded from https://wits.worldbank.org/.

Acknowledgements

We sincerely thank the Editor, the Associate Editor, and two reviewers for their valuable feedback and constructive suggestions, which have helped improve the quality and clarity of our manuscript.

    Funding

    Mu Zhu and Peijun Sang are supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada under grants RGPIN-2023-03337 and RGPIN-2020-04602, respectively.

    Appendix A: MLE of β ^ 0 $$ {\hat{\beta}}_0 $$

    In this section, we provide the detailed derivation of β ^ 0 ( β ( t ) ) $$ {\hat{\boldsymbol{\beta}}}_0\left(\boldsymbol{\beta} (t)\right) $$ as defined in expression (9). Subsequently, we substitute this resulting maximum likelihood estimate of β ^ 0 $$ {\hat{\beta}}_0 $$ back into expression (9), demonstrating how the equation presented in the first line of statement (10) is established.

    The derivative of (9) with respect to β 0 k ℓ $$ {\beta}_0^{k\mathit{\ell}} $$ is given by
    ∂ ℓ n ( β 0 , β ( t ) , ϕ 0 , ρ 0 ; D , z ) ∂ β 0 k ℓ = 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n 1 ( z i = k , z j = ℓ ) ϕ 0 × y i j ( t ν ) · exp [ ( 1 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] − exp [ ( 2 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] . $$ {\displaystyle \begin{array}{ll}\hfill \frac{\partial {\ell}_n\left({\boldsymbol{\beta}}_0,\boldsymbol{\beta} (t),{\phi}_0,{\rho}_0;D,z\right)}{\partial {\beta}_0^{k\mathit{\ell}}}& =\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\\ {}& \kern1em \times \left\{{y}_{ij}\left({t}_{\nu}\right)\cdotp \exp \left[\left(1-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]-\exp \left[\left(2-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]\right\}.\end{array}} $$ (A1)
    Thus, the second-order derivative is
    ∂ 2 ℓ n ( β 0 , β ( t ) , ϕ 0 , ρ 0 ; D , z ) ∂ [ β 0 k ℓ ] 2 = 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n 1 ( z i = k , z j = ℓ ) ϕ 0 × ( 1 − ρ 0 ) · y i j ( t ν ) · exp [ ( 1 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] − ( 2 − ρ 0 ) · exp [ ( 2 − ρ 0 ) { β 0 k ℓ + x i j ⊤ β ( t ν ) } ] < 0 . $$ {\displaystyle \begin{array}{ll}& \frac{\partial^2{\ell}_n\left({\boldsymbol{\beta}}_0,\boldsymbol{\beta} (t),{\phi}_0,{\rho}_0;D,z\right)}{\partial {\left[{\beta}_0^{k\mathit{\ell}}\right]}^2}\\ {}& \kern1em =\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\times \left\{\left(1-{\rho}_0\right)\cdotp {y}_{ij}\left({t}_{\nu}\right)\cdotp \exp \left[\left(1-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]\right.\\ {}& \kern2em -\left.\left(2-{\rho}_0\right)\cdotp \exp \left[\left(2-{\rho}_0\right)\left\{{\beta}_0^{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]\right\}<0.\end{array}} $$
    Therefore, the MLE of β 0 k ℓ $$ {\beta}_0^{k\mathit{\ell}} $$ is given by the zero of expression (A1) as
    β ^ 0 k ℓ ( β ( t ) ) = log ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n y i j ( t ν ) exp [ ( 1 − ρ ) x i j ⊤ β ( t ν ) ] 1 ( z i = k , z j = ℓ ) ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n exp [ ( 2 − ρ ) x i j ⊤ β ( t ν ) ] 1 ( z i = k , z j = ℓ ) = log θ ^ k ℓ γ ^ k ℓ . $$ {\displaystyle \begin{array}{ll}\hfill {\hat{\beta}}_0^{k\mathit{\ell}}\left(\boldsymbol{\beta} (t)\right)& =\log \frac{\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}{y}_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\exp \left[\left(2-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}\\ {}\hfill & =\log \frac{{\hat{\theta}}_{k\mathit{\ell}}}{{\hat{\gamma}}_{k\mathit{\ell}}}.\end{array}} $$
    Plugging β ^ 0 k ℓ ( β ( t ) ) = log θ ^ k ℓ / γ ^ k ℓ $$ {\hat{\beta}}_0^{k\mathit{\ell}}\left(\boldsymbol{\beta} (t)\right)=\log {\hat{\theta}}_{k\mathit{\ell}}/{\hat{\gamma}}_{k\mathit{\ell}} $$ into expression (9), we obtain the first line of the equation presented in expression (10):
    ℓ n ( β ( t ) , ϕ 0 , ρ 0 ; D , z ) = 1 n 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n ∑ k , ℓ = 1 K 1 ( z i = k , z j = ℓ ) ϕ 0 × y i j ( t ν ) exp [ ( 1 − ρ 0 ) { log θ ^ k ℓ / γ ^ k ℓ + x i j ⊤ β ( t ν ) } ] 1 − ρ 0 − exp [ ( 2 − ρ 0 ) { log θ ^ k ℓ / γ ^ k ℓ + x i j ⊤ β ( t ν ) } ] 2 − ρ 0 = 1 n 2 ∑ k , ℓ = 1 K 1 1 − ρ 0 θ ^ k ℓ γ ^ k ℓ 1 − ρ 0 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n 1 ( z i = k , z j = ℓ ) ϕ 0 · y i j ( t ν ) exp [ ( 1 − ρ 0 ) { x i j ⊤ β ( t ν ) } ] − 1 n 2 ∑ k , ℓ = 1 K 1 2 − ρ 0 θ ^ k ℓ γ ^ k ℓ 2 − ρ 0 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n 1 ( z i = k , z j = ℓ ) ϕ 0 · exp [ ( 2 − ρ 0 ) { x i j ⊤ β ( t ν ) } ] = 1 ϕ 0 ∑ k , ℓ = 1 K 1 1 − ρ 0 θ ^ k ℓ γ ^ k ℓ 1 − ρ 0 · θ ^ k ℓ − 1 ϕ 0 ∑ k , ℓ = 1 K 1 2 − ρ 0 ( θ ^ k ℓ γ ^ k ℓ ) 2 − ρ 0 · γ ^ k ℓ = 1 ϕ 0 1 ( 1 − ρ 0 ) ( 2 − ρ 0 ) ∑ k , ℓ = 1 K θ ^ k ℓ 2 − ρ 0 · γ ^ k ℓ ρ 0 − 1 . $$ {\displaystyle \begin{array}{ll}\hfill & {\ell}_n\left(\boldsymbol{\beta} (t),{\phi}_0,{\rho}_0;D,z\right)=\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\sum \limits_{k,\ell =1}^K\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\\ {}\hfill & \kern2em \times \left[\frac{y_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-{\rho}_0\right)\left\{\log {\hat{\theta}}_{k\mathit{\ell}}/{\hat{\gamma}}_{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{1-{\rho}_0}-\frac{\exp \left[\left(2-{\rho}_0\right)\left\{\log {\hat{\theta}}_{k\mathit{\ell}}/{\hat{\gamma}}_{k\mathit{\ell}}+{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]}{2-{\rho}_0}\right]\\ {}& \kern1em =\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{k,\ell =1}^K\frac{1}{1-{\rho}_0}{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{1-{\rho}_0}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\cdotp {y}_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-{\rho}_0\right)\left\{{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]\\ {}\hfill & \kern2em -\frac{1}{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\sum \limits_{k,\ell =1}^K\frac{1}{2-{\rho}_0}{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{2-{\rho}_0}\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\frac{\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)}{\phi_0}\cdotp \exp \left[\left(2-{\rho}_0\right)\left\{{\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right\}\right]\\ {}& \kern1em =\frac{1}{\phi_0}\sum \limits_{k,\ell =1}^K\frac{1}{1-{\rho}_0}{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{1-{\rho}_0}\cdotp {\hat{\theta}}_{k\mathit{\ell}}-\frac{1}{\phi_0}\sum \limits_{k,\ell =1}^K\frac{1}{2-{\rho}_0}{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{2-{\rho}_0}\cdotp {\hat{\gamma}}_{k\mathit{\ell}}\\ {}& \kern1em =\frac{1}{\phi_0}\frac{1}{\left(1-{\rho}_0\right)\left(2-{\rho}_0\right)}\sum \limits_{k,\ell =1}^K{\hat{\theta}}_{k\mathit{\ell}}^{2-{\rho}_0}\cdotp {\hat{\gamma}}_{k\mathit{\ell}}^{\rho_0-1}.\end{array}} $$

    Appendix B: Proof of Theorem 1

    In this section, we prove Theorem 1. Before laying out the main proof, we first introduce several lemmas.

    Lemma 1.Under Conditions 3.1 and 3.2,

    γ ^ k ℓ ∑ k , ℓ γ ^ k ℓ = p k p ℓ + o p ( 1 ) . $$ \frac{{\hat{\gamma}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}}={p}_k{p}_{\ell }+{o}_p(1). $$

    Proof.According to Conditions 3.1 and 3.2, exp [ ( 2 − ρ ) x i j ⊤ β ( t ) ] $$ \exp \left[\left(2-\rho \right){x}_{ij}^{\top}\beta (t)\right] $$ and 1 ( z i = k , z j = ℓ ) $$ \mathbbm{1}\left({z}_i=k,{z}_j=\ell \right) $$ are iid random variables, with mean γ $$ \gamma $$ and p k p ℓ $$ {p}_k{p}_{\ell } $$ respectively. Specifically, γ $$ \gamma $$ is a positive constant. By the weak law of large numbers, we have

    γ ^ k ℓ ∑ k , ℓ γ ^ k ℓ = 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n exp [ ( 2 − ρ ) x i j ⊤ β ( t ν ) ] 1 ( z i = k , z j = ℓ ) / { n ( n − 1 ) } 2 ∑ ν = 1 T ∑ 1 ≤ i < j ≤ n exp [ ( 2 − ρ ) x i j ⊤ β ( t ν ) ] / { n ( n − 1 ) } = γ · p k p ℓ + o p ( 1 ) γ + o p ( 1 ) = p k p ℓ + o p ( 1 ) . $$ {\displaystyle \begin{array}{ll}\hfill \frac{{\hat{\gamma}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}}& =\frac{2\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\exp \left[\left(2-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]\mathbbm{1}\left({z}_i=k,{z}_j=\ell \right)/\left\{n\left(n-1\right)\right\}}{2\sum \limits_{\nu =1}^T\sum \limits_{1\le i<j\le n}\exp \left[\left(2-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right]/\left\{n\left(n-1\right)\right\}}\\ {}\hfill & =\frac{\gamma \cdotp {p}_k{p}_{\ell }+{o}_p(1)}{\gamma +{o}_p(1)}\\ {}\hfill & ={p}_k{p}_{\ell }+{o}_p(1).\end{array}} $$

    Lemma 2.Under Conditions 3.1 and 3.2,

    θ ^ k ℓ ∑ k , ℓ θ ^ k ℓ = p k p ℓ + o p ( 1 ) . $$ \frac{{\hat{\theta}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}}={p}_k{p}_{\ell }+{o}_p(1). $$

    Proof.The proof is similar to that of Lemma 1. If we can show that, at each time point t ν $$ {t}_{\nu } $$ , ν ∈ { 1 , … , T } $$ \nu \in \left\{1,\dots, T\right\} $$ , y i j ( t ν ) exp [ ( 1 − ρ ) x i j ⊤ β ( t ν ) ] $$ {y}_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right] $$ for i , j ∈ { 1 , … , n } $$ i,j\in \left\{1,\dots, n\right\} $$ are iid with a nonzero mean, we complete the proof. For each node pair ( i , j ) $$ \left(i,j\right) $$ , both their pairwise covariate x i j $$ {\boldsymbol{x}}_{ij} $$ and community labels c i $$ {c}_i $$ and c j $$ {c}_j $$ are iid. Moreover, y i j ( t ν ) $$ {y}_{ij}\left({t}_{\nu}\right) $$ conditional on x i j $$ {x}_{ij} $$ , c i $$ {c}_i $$ and c j $$ {c}_j $$ are iid as well. Therefore, y i j ( t ν ) exp [ ( 1 − ρ ) x i j ⊤ β ( t ν ) ] $$ {y}_{ij}\left({t}_{\nu}\right)\exp \left[\left(1-\rho \right){\boldsymbol{x}}_{ij}^{\top}\boldsymbol{\beta} \left({t}_{\nu}\right)\right] $$ for i , j ∈ { 1 , … , n } $$ i,j\in \left\{1,\dots, n\right\} $$ are iid, with mean

    𝔼 [ y i j ( t ν ) exp { ( 1 − ρ ) x i j ⊤ β ( t ν ) } ] = 𝔼 𝔼 [ y i j ( t ν ) exp { ( 1 − ρ ) x i j ⊤ β ( t ν ) } | x , c ] = 𝔼 𝔼 { y i j ( t ν ) | x , c } · exp { ( 1 − ρ ) x i j ⊤ β ( t ν ) } = 𝔼 exp { β 0 c i c j + x i j ⊤ β ( t ν ) } · exp { ( 1 − ρ ) x i j ⊤ β ( t ν ) } = ∑ k , ℓ 𝔼 exp β 0 k ℓ + ( 2 − ρ ) x i j ⊤ β ( t ν ) · p k p ℓ .
    Therefore, the expectation is a nonzero constant.

    Next, we prove Theorem 1.

    Proof of Theorem 1.By Lemmas 1 and 2 and the Continuous Mapping Theorem,

    ∑ k , ℓ θ ^ k ℓ 2 − ρ · γ ^ k ℓ ρ − 1 = ∑ k , ℓ θ ^ k ℓ ∑ k , ℓ θ ^ k ℓ 2 − ρ · γ ^ k ℓ ∑ k , ℓ γ ^ k ℓ ρ − 1 · ∑ k , ℓ θ ^ k ℓ 2 − ρ ∑ k , ℓ γ ^ k ℓ ρ − 1 = ∑ k , ℓ ( p k p ℓ ) 2 − ρ + o p ( 1 ) · ( p k p ℓ ) ρ − 1 + o p ( 1 ) · ∑ k , ℓ θ ^ k ℓ 2 − ρ ∑ k , ℓ γ ^ k ℓ ρ − 1 = ∑ k , ℓ p k p ℓ + o p ( 1 ) · ∑ k , ℓ θ ^ k ℓ 2 − ρ ∑ k , ℓ γ ^ k ℓ ρ − 1 = 1 + K ( K + 1 ) 2 o p ( 1 ) · θ + o p ( 1 ) 2 − ρ γ + o p ( 1 ) ρ − 1 = θ 2 − ρ γ ρ − 1 + o p ( 1 ) . $$ {\displaystyle \begin{array}{ll}\hfill & \sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}^{2-\rho}\cdotp {\hat{\gamma}}_{k\mathit{\ell}}^{\rho -1}\\ {}& \kern1em =\left[\sum \limits_{k,\ell }{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}}\right)}^{2-\rho}\cdotp {\left(\frac{{\hat{\gamma}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{\rho -1}\right]\cdotp {\left(\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}\right)}^{2-\rho }{\left(\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}\right)}^{\rho -1}\\ {}& \kern1em =\left[\sum \limits_{k,\ell}\left\{{\left({p}_k{p}_{\ell}\right)}^{2-\rho }+{o}_p(1)\right\}\cdotp \left\{{\left({p}_k{p}_{\ell}\right)}^{\rho -1}+{o}_p(1)\right\}\right]\cdotp {\left(\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}\right)}^{2-\rho }{\left(\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}\right)}^{\rho -1}\\ {}& \kern1em =\left[\sum \limits_{k,\ell}\left({p}_k{p}_{\ell }+{o}_p(1)\right)\right]\cdotp {\left(\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}\right)}^{2-\rho }{\left(\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}\right)}^{\rho -1}\\ {}& \kern1em =\left[1+\frac{K\left(K+1\right)}{2}{o}_p(1)\right]\cdotp {\left(\theta +{o}_p(1)\right)}^{2-\rho }{\left(\gamma +{o}_p(1)\right)}^{\rho -1}\\ {}& \kern1em ={\theta}^{2-\rho }{\gamma}^{\rho -1}+{o}_p(1).\end{array}} $$ (B1)
    Equation (B1) holds because ∑ k , ℓ θ ^ k ℓ = θ ^ = θ + o p ( 1 ) $$ {\sum}_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}=\hat{\theta}=\theta +{o}_p(1) $$ and ∑ k , ℓ γ ^ k ℓ = γ ^ = γ + o p ( 1 ) $$ {\sum}_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}=\hat{\gamma}=\gamma +{o}_p(1) $$ by the weak law of large numbers. Therefore, we have
    2 n ( n − 1 ) l z ( β ( t ) ) = 1 ϕ 1 ( 1 − ρ ) ( 2 − ρ ) ∑ k , ℓ θ ^ k ℓ 2 − ρ · γ ^ k ℓ ρ − 1 = 1 ϕ 1 ( 1 − ρ ) ( 2 − ρ ) θ 2 − ρ · γ ρ − 1 + o p ( 1 ) = 1 ϕ 1 ( 1 − ρ ) ( 2 − ρ ) θ 2 − ρ · γ ρ − 1 + o p ( 1 ) . $$ {\displaystyle \begin{array}{ll}\hfill \frac{2}{n\left(n-1\right)}{l}_z\left(\boldsymbol{\beta} (t)\right)& =\frac{1}{\phi}\frac{1}{\left(1-\rho \right)\left(2-\rho \right)}\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}^{2-\rho}\cdotp {\hat{\gamma}}_{k\mathit{\ell}}^{\rho -1}\\ {}\hfill & =\frac{1}{\phi}\frac{1}{\left(1-\rho \right)\left(2-\rho \right)}\left({\theta}^{2-\rho}\cdotp {\gamma}^{\rho -1}+{o}_p(1)\right)\\ {}\hfill & =\frac{1}{\phi}\frac{1}{\left(1-\rho \right)\left(2-\rho \right)}{\theta}^{2-\rho}\cdotp {\gamma}^{\rho -1}+{o}_p(1).\end{array}} $$

    Remark 2.By Hölder's inequality, we have

    ∑ k , ℓ θ ^ k ℓ ∑ k , ℓ θ ^ k ℓ 2 − ρ · γ ^ k ℓ ∑ k , ℓ γ ^ k ℓ ρ − 1 ≤ ∑ k , ℓ θ ^ k ℓ ∑ k , ℓ θ ^ k ℓ 2 − ρ · ∑ k , ℓ γ ^ k ℓ ∑ k , ℓ γ ^ k ℓ ρ − 1 = 1 . $$ \sum \limits_{k,\ell }{\left(\frac{{\hat{\theta}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}}\right)}^{2-\rho}\cdotp {\left(\frac{{\hat{\gamma}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{\rho -1}\le {\left(\sum \limits_{k,\ell}\frac{{\hat{\theta}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\theta}}_{k\mathit{\ell}}}\right)}^{2-\rho}\cdotp {\left(\sum \limits_{k,\ell}\frac{{\hat{\gamma}}_{k\mathit{\ell}}}{\sum \limits_{k,\ell }{\hat{\gamma}}_{k\mathit{\ell}}}\right)}^{\rho -1}=1. $$
    Then, it follows
    2 n ( n − 1 ) l z ( β ( t ) ) ≤ 1 ϕ 1 ( 1 − ρ ) ( 2 − ρ ) θ 2 − ρ · γ ρ − 1 . $$ \frac{2}{n\left(n-1\right)}{l}_z\left(\boldsymbol{\beta} (t)\right)\le \frac{1}{\phi}\frac{1}{\left(1-\rho \right)\left(2-\rho \right)}{\theta}^{2-\rho}\cdotp {\gamma}^{\rho -1}. $$ (B2)
    In fact, Lemmas 1 and 2 establish the asymptotic equality conditions, which sharpen the inequality (B2) and lead to the conclusion in Theorem 1.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.