1 Background

Radiation therapy (RT) is a crucial method for cancer treatment, working to control the spread of cancer using high-energy radiation to kill malignant cells. In recent years, there have been remarkable improvements in the treatment planning quality due to the introduction of intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT) [1, 2]. However, this progress comes with the trade-off of increased complexity, especially when planning therapy in intricate areas, and it often requires multiple attempts and invests a substantial amount of time to enhance plan quality.

Researchers have been actively working to address these challenges. Knowledge-based planning (KBP) methods [3, 4], widely applied in recent years, primarily rely on historical treatment planning data for each patient as a reference to create dose distribution plans for new clinical treatments. The dose–volume histogram (DVH) [5] is a clinical evaluation metric that is commonly used in KBP methods, which can help automate radiotherapy planning. However, KBP methods still have several critical limitations. First, they rely heavily on handcrafted features corresponding to the dose distribution [6]. The extraction of features is not only timeconsuming but also lacks accuracy. Second, the features extracted by DVH lack spatial details about dose distributions [7], due to the compression and asymmetric mapping of three-dimensional (3D) dose information. Moreover, these methods fail to consider anatomical structures and location information around tumors, thus neglecting the influence of surrounding organs.

Most recently, convolutional neural networks (CNNs) have made remarkable breakthroughs in medical image analysis [8, 9], leading to their application in radiotherapy dose prediction, with 3D UNet and its variants being the predominant models. Nguyen et al. [10] and Alexander et al. [11] proposed hierarchically densely connected UNet and attention-aware 3D UNet, respectively, for IMRT 3D dose distribution prediction in head and neck cancer. Li et al. [12] proposed a multitask attention adversarial network to automatically complete dose planning in cervical cancer, in which UNet served as the main architecture for the dose decoder and auxiliary segmentation. Similar studies can also be found in breast cancer [7], colorectal cancer [13], and prostate cancer [14].

Despite these successes, there is room for improvement in prediction accuracy. First, progressive feature fusion contributes to enhancing the depth and effectiveness of features, thus improving the modeling capability. Second, difficult regions should be considered to prevent models from taking shortcuts by optimizing only for easy areas, improving clinical relevance. Furthermore, with specifically designed training constraints, models can be explicitly guided to focus on high-dose regions, leading to increased dose prediction accuracy. Finally, most current research efforts mainly aim to enhance dose prediction accuracy. Nonetheless, a considerable lack of investigations exists on how dose prediction can influence the quality of planning, a crucial aspect of clinical care.

To this end, we propose herein DESIRE, a Dose prediction model with progrEssive feature fuSion and dIfficult Region lEarning in this study, illustrating its use in a study of patients with nasopharyngeal carcinoma (NPC) after VMAT. First, a progressive UNet was designed for feature extraction and effective information fusion, incorporating a residual dense (RD) block to enhance learning capabilities further. Moreover, to explicitly enforce the constraints closely related to the dose prediction task, we proposed a novel loss function that can guide the model to focus on difficult regions and high-dose areas during training. We compared our proposed DESIRE model with several state-of-the-art methods using an indoor validation dataset from patients with NPC to validate its feasibility in dose prediction. Meanwhile, two junior physicians were invited to reference the dose prediction results of the DESIRE for treatment planning. The quality of their plans was compared with that of senior physicians to assess the potential clinical value of the model.

2 Methods

2.3 Model and Training

2.3.1 Overall Model Architecture

As shown in Figure 1, DESIRE consists of two progressive UNet architectures (Figure 1a). It starts by employing a 4-layer UNet structure for initial feature extraction. Subsequently, a channel attention module (Figure 1d) transforms the extracted features of the four upsampling layers into attention weights, which are then applied to the second UNet. The second UNet is a five-layer structure, with each layer having twice the number of channels as the corresponding layer in the first UNet. Its input consists of the features from the previous layer and the corresponding feature generated from the first UNet. In this way, more effective feature extraction and fusion can be achieved in terms of both network depth and width.

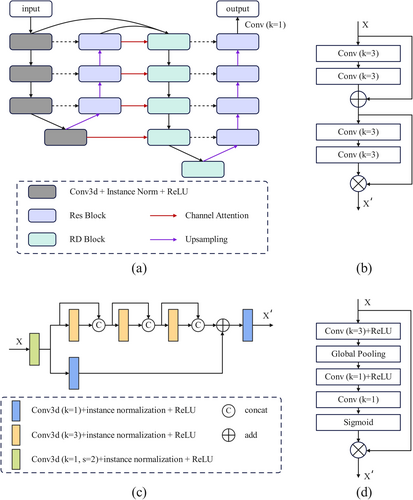
Both encoders of the two UNets replace the max-pooling layers with convolution layers with a stride of two for down-sampling operations. The first encoder utilizes a standard 3D convolution module, whereas the second encoder employs an RD block (Figure 1c) to enhance feature extraction. For the decoder, trilinear interpolation is used for feature upsampling, and feature fusion is implemented by residual modules (Figure 1b). Finally, a 1 × 1 × 1 convolution is used to generate the final prediction.

2.3.2 Residual Dense Block

The residual connections of ResNet and the dense connections from DenseNet are effectively integrated into a new RD block, as illustrated in Figure 1c. The RD block begins by down-sampling through a 3D convolution with a stride of two. Afterward, two separate processing branches are used for different feature transformations. The upper branch consists of three convolution modules, each concatenating the original feature and transformed features generated by current convolution operations. For the other branch, a 1 × 1 × 1 convolution is used to obtain local features. The results from both branches are then fused by element-wise summation, followed by another 1 × 1 × 1 convolution. In this way, the global features from the upper branch and the local features from the lower branch are integrated. All the convolution operations are followed by instance normalization and a ReLU activation function.

2.3.3 Difficult Region Learning

Dose prediction is a pixel-level regression task. With currently widely used loss functions, such as the mean average error loss, CNNs are prone to pay more attention to the regions that are easy to learn while ignoring more difficult, but important, areas. We introduced difficult region learning loss to explicitly guide the model to be more attentive to difficult regions, as illustrated in Figure 2.

First, we used the mean squared error to calculate the difference, denoted as $$$ {L}_{MSE} $$$, between the model prediction and GT. Next, we substitute the model's standard output with four dropout outputs, each with distinct probability distributions. The objective is to empower the model to acquire four outputs characterized by enhanced diversity and randomness in a single forward propagation iteration. The four dropout outputs are separately processed through two branches. In the first branch, the four dropout outputs are processed with the function $$$ {f}_1 $$$ to calculate the variance and normalization, resulting in the first weight map. The formula for $$$ {f}_1 $$$ is shown in Equation (1). In the second branch, we calculate the mean of the four dropout outputs and subtract it from the $$$ GT $$$. Then, with the function $$$ {f}_2 $$$, as shown in Equation (2), the second weight map is obtained. Afterward, the $$$ {Loss}_{MSE} $$$ is used to calculate the difference between the generated two weight maps, which is then used to obtain the final difficult region learning loss $$$ {L}_{DR} $$$, as shown in Equation (3). Here, $$$ m $$$ is the number of samples, $$$ {d}_1 $$$, $$$ {d}_2 $$$, $$$ {d}_3 $$$, and $$$ {d}_4 $$$ are the results of the four dropout predictions, $$$ Var(D) $$$ is their variance, $$$ Mean(D) $$$ is the average, and $$$ \alpha $$$ and $$$ \beta $$$ are the hyper-parameters for proper adjustment of the normalization mapping and pay more attention on difficult regions. In our experiments, we experimentally set α and β as 0.5 and 0.05, respectively.

$$$$ {f}_1=f\left({d}_1,{d}_2,{d}_3,{d}_4\right)=\frac{Var(D)}{\alpha + Var(D)} $$$$()

$$$$ {f}_2=f\left({d}_1,{d}_2,{d}_3,{d}_4\right)=\frac{\left| Mean(D)- GT\right|}{\beta +\left| Mean(D)- GT\right|} $$$$()

$$$$ {L}_{DR}=\frac{1}{m}\sum \limits_{n=1}^m\left({f}_1+{f}_2\right)\bullet {\left|{y}_n-\hat{y_n}\right|}^2 $$$$()

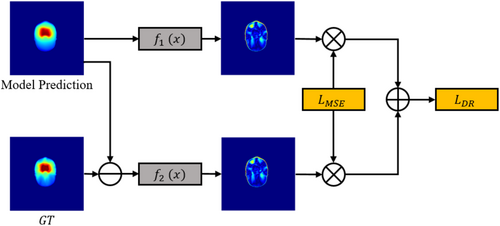
2.3.4 Auxiliary Segmentation Loss

For the dose distribution map, there are regions where the values exceed the prescribed dose, which require more attention weight. Therefore, a semantic segmentation loss function is employed to enforce the model to focus on the high-dose regions explicitly. Figure 3a represents the dose distribution map, with a prescription dose of 70 Gy for PTVnx. We labeled the regions where the dose is greater than or equal to 70 Gy as the high-dose regions (Figure 3b). The combination of the binary cross-entropy (BCE) and Dice loss functions is used to compute the difference between the dose prediction results and the $$$ GT $$$ within those high-dose regions:

$$$$ {L}_{seg}=\frac{1}{k}\sum \limits_{n=1}^k\left(0.5\times {BCELoss}_n+0.5\times {DICELoss}_n\right) $$$$()

Here, $$$ k $$$ denotes the number of high-dose regions.

2.3.5 Final Loss

The final loss $$$ {L}_{final} $$$ is the combination of mean absolute error (MAE) loss $$$ {L}_{MAE} $$$, difficult region learning loss $$$ {L}_{DR} $$$, and the auxiliary segmentation loss $$$ {L}_{seg} $$$:

$$$$ {L}_{final}={L}_{MAE}+{L}_{DR}+\gamma \times {L}_{seg} $$$$()

Here, $$$ \gamma $$$ adjusts the weight of the auxiliary segmentation loss, and we experimentally set it as 0.1 to prevent an excessively high auxiliary segmentation loss weight, which could decrease the final dose prediction performance.

3 Results

3.1 Dosimetric Metrics Comparison

Table 1 demonstrates the dosimetric metric differences for PTVs between the dose distribution predicted by DESIRE and the corresponding metrics of the actual dose distribution, expressed as means ± standard deviations. The D₉₅ values for DESIRE concerning PTV70, PTV60, and PTV55 were 70.03 Gy, 62.13 Gy, and 55.67 Gy, respectively, which meet clinical acceptability criteria. Additionally, most mean differences in D₉₈, D₉₅, D₅₀, and D_mean between DESIRE and GT were below 1 Gy, with the mean differences in D₂ being less than 1.6 Gy.

TABLE 1. Difference in dosimetric metrics between the proposed DESIRE model and ground truth (mean ± standard deviation) on testing cohort (N = 20).

		PTV70 (Gy)	PTV60 (Gy)	PTV55 (Gy)
D 98	GT	69.79 ± 0.39	60.65 ± 0.70	54.11 ± 0.47
	PRED	68.79 ± 0.35	60.88 ± 0.98	54.03 ± 0.42
	DIFF	−1.00 ± 0.41	0.23 ± 0.76	−0.08 ± 0.64
	p	0.00	0.30	0.64
D 95	GT	70.62 ± 0.69	61.68 ± 0.71	55.38 ± 0.46
	PRED	70.03 ± 0.08	62.13 ± 0.92	55.67 ± 0.53
	DIFF	−0.60 ± 0.71	0.45 ± 0.74	0.29 ± 0.71
	p	0.00	0.07	0.07
D 50	GT	72.46 ± 0.53	69.24 ± 1.48	60.46 ± 1.99
	PRED	73.43 ± 0.82	69.88 ± 1.27	61.28 ± 1.82
	DIFF	0.97 ± 1.04	0.64 ± 0.76	0.82 ± 1.69
	p	0.00	0.05	0.08
D 2	GT	73.90 ± 0.63	73.44 ± 0.59	73.33 ± 0.64
	PRED	75.45 ± 0.78	74.66 ± 0.68	74.55 ± 0.84
	DIFF	1.55 ± 0.87	1.22 ± 0.82	1.22 ± 0.88
	p	0.00	0.00	0.00
D mean	GT	72.27 ± 0.51	68.41 ± 0.82	62.45 ± 1.29
	PRED	73.19 ± 0.64	69.34 ± 0.96	63.18 ± 1.16
	DIFF	0.92 ± 0.82	0.93 ± 0.64	0.73 ± 0.67
	p	0.00	0.00	0.08

• Abbreviations: DIFF, difference, calculated by subtracting GT from PRED; GT, ground truth; PRED, prediction of DESIRE.

Table 2 displays the D₁ and D_mean for the OARs. Overall, there was no significant difference between the predictions of DESIRE and the GT in terms of both D₁ and D_mean. The mean difference in D_mean was around 1 Gy, and that in D₁ was around 1.5 Gy.

TABLE 2. $$$ {D}_{mean} $$$ and $$$ {D}_1 $$$ for OARs (mean ± standard deviation) on testing cohort (N = 20).

	Dmean (Gy)				D1 (Gy)
	GT	PRED	DIFF	p	GT	PRED	DIFF	p
Brainstem	30.12 ± 6.12	30.94 ± 4.99	0.82 ± 3.44	0.88	50.76 ± 4.95	51.26 ± 4.82	0.50 ± 4.60	0.92
L eye	7.54 ± 3.42	8.22 ± 4.11	0.67 ± 2.17	0.84	21.13 ± 9.01	23.21 ± 11.34	2.09 ± 6.29	0.64
R eye	7.55 ± 3.19	8.25 ± 4.18	0.71 ± 2.96	0.92	21.61 ± 9.79	21.99 ± 10.49	0.38 ± 7.38	0.86
L len	4.98 ± 1.57	5.63 ± 2.53	0.65 ± 1.52	0.76	6.18 ± 2.34	7.72 ± 4.21	1.54 ± 2.72	0.39
R len	4.89 ± 1.33	5.99 ± 3.57	1.10 ± 3.12	0.80	5.95 ± 1.86	7.71 ± 4.91	1.76 ± 4.40	0.62
L middle ear	47.29 ± 7.92	48.35 ± 7.88	1.05 ± 2.98	0.54	65.16 ± 5.92	64.70 ± 6.44	−0.46 ± 2.32	0.74
R middle ear	42.15 ± 8.05	43.43 ± 7.94	1.27 ± 3.68	0.49	61.34 ± 6.32	60.76 ± 6.94	−0.58 ± 2.39	0.78
L optic nerve	25.17 ± 13.99	26.35 ± 13.97	1.17 ± 4.62	0.88	40.94 ± 18.62	43.92 ± 18.24	2.98 ± 5.66	0.69
R optic nerve	23.64 ± 12.55	25.39 ± 13.31	1.76 ± 4.22	0.68	39.16 ± 16.05	42.66 ± 16.88	3.50 ± 5.30	0.34
L parotid	36.07 ± 7.21	37.11 ± 6.55	1.05 ± 3.01	0.39	66.16 ± 5.46	65.63 ± 6.04	−0.53 ± 1.99	0.86
R parotid	34.92 ± 4.16	36.51 ± 4.14	1.59 ± 2.86	0.20	67.88 ± 5.64	67.50 ± 5.35	−0.38 ± 2.55	0.84
L temporal lobe	14.57 ± 4.27	14.48 ± 4.22	−0.09 ± 1.41	0.90	59.15 ± 5.67	60.42 ± 5.06	1.27 ± 2.84	0.39
R temporal lobe	14.14 ± 4.53	13.81 ± 4.45	−0.33 ± 0.92	0.78	57.03 ± 5.86	57.94 ± 6.54	0.90 ± 2.30	0.54
L TMJ	44.22 ± 8.18	44.17 ± 7.37	−0.05 ± 2.21	0.99	59.03 ± 8.28	58.45 ± 7.37	−0.58 ± 2.00	0.95
R TMJ	39.68 ± 8.02	40.31 ± 7.41	0.64 ± 2.80	0.62	53.83 ± 9.03	53.98 ± 8.40	0.14 ± 3.01	0.95
Larynx	39.85 ± 3.40	40.33 ± 2.88	0.48 ± 3.69	0.68	60.53 ± 5.21	60.30 ± 5.17	−0.23 ± 2.10	0.95
Optic chiasma	27.46 ± 13.60	29.67 ± 14.22	2.21 ± 4.67	0.52	37.73 ± 16.55	40.36 ± 16.17	2.63 ± 5.57	0.56
Oral cavity	37.93 ± 4.27	38.78 ± 3.73	0.85 ± 1.90	0.44	62.78 ± 6.59	62.55 ± 6.03	−0.23 ± 1.65	0.97
Spinal cord	27.34 ± 2.44	27.65 ± 2.68	0.31 ± 1.44	0.76	36.89 ± 1.01	37.78 ± 2.00	0.89 ± 2.20	0.11

• Abbreviations: DIFF, difference, calculated by subtracting GT from PRED; GT, ground truth; PRED, prediction of DESIRE.

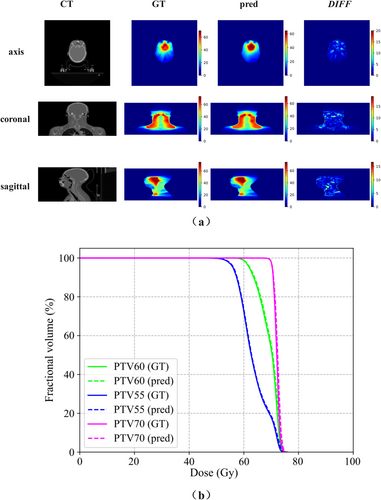
To further visualize dose differences, the qualitative results of one case are shown in Figure 4, providing a more intuitive understanding of the model's predictive capabilities. The predicted dose distribution was relatively smooth, with minimal differences in individual pixels at the edges of some target areas, indicating no significant prediction errors. Figure 4b compares the GT DVHs of the PTVs and the DVHs predicted by the DESIRE for one patient in the test set. For all three PTVs, the dose curves predicted by DESIRE closely matched the real dose distribution curves, indicating satisfactory performance and clinical applicability.

3.2 Gamma Pass Rate for PTVs

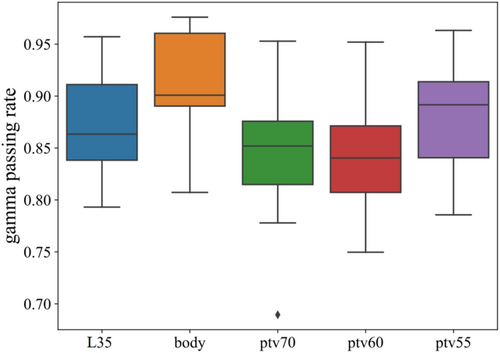
The PTVs in the 3D gamma analysis comprise the region delineated by the 35-Gy isodose line (referred to as L35), the body, PTV70, PTV60, and PTV55. The box plot illustrating the gamma passing rate for PTVs is presented in Figure 5. The average passing rates were 87.4%, 91.3%, 84.7%, 84.1%, and 88.3%.

4 Discussion

Recent technological advances have caused radiotherapy to become highly complex, with software and hardware that are almost entirely dependent on human–computer interactions. Precise automated dose prediction holds the potential to substantially enhance both the efficiency and safety of clinical treatment planning. The results obtained from 3D dose prediction can be directly applied to the ongoing optimization of radiation therapy plans within the treatment planning system. In this study, we developed DESIRE. In routine clinical practice, variations in the planning process arise due to different physicians consulting with patients, introducing an element of uncertainty in radiation therapy planning results. Employing CNN-based dose predictions to guide the plan optimization process can mitigate this uncertainty and concurrently enhance the efficiency of plan optimization.

In recent years, extensive research has applied deep learning to dose prediction tasks, with UNet and its variants predominating. Liu et al. [20] proposed a deep learning method for dose prediction based on the cascade mechanism and 3D UNet by taking advantage of data augmentations. They achieved MAE values of 2.50 Gy for a single C3D model without test-time augmentation and a DVH score of 1.55. Using an attention-gating mechanism and a 3D UNet for IMRT 3D dose distribution prediction in head and neck cancer, Osman et al. [11] also found that the average difference in predicting the D₉₉ value for the targets was 2.50 ± 1.77 Gy. For the OARs, the average differences in predicting the D_max and D_mean values were 1.43 ± 1.01 Gy and 2.44 ± 1.73 Gy, respectively. The average value of the HI was 7.99 ± 1.45, and the CI was 0.63 ± 0.17 for the predicted plans. Nguyen et al. [10] proposed a 3D radiotherapy dose prediction method in head and neck cancer with a hierarchically densely connected UNet architecture and achieved an average prediction difference of maximum dose within 6.3% and mean dose within 5.1% of the prescription dose on test data across all OARs. Previous findings have demonstrated the potential and feasibility of UNet models. Despite their success, several aspects can be further improved for higher prediction accuracy. In this study, various strategies, such as progressive feature fusion and difficult region learning, were introduced. Our model underwent rigorous training and validation using a private dataset encompassing data from 131 patients with NPC. Comprehensive quantitative assessments have validated the model's clinical significance. Furthermore, we conducted comparative analyses with several state-of-the-art UNet-based methods, the DESIRE model demonstrated dose predictions that align closely with the ground truth generated by an experienced dosimetrist, further research is needed to assess whether DESIRE's dose predictions result in optimal dose distributions and to evaluate its impact on plan quality and clinical outcomes.

Existing studies on dose prediction have mostly focused on improving the accuracy of dose prediction models while neglecting the evaluation of their true clinical applicability. In this study, we investigated how dose prediction can improve the quality of planning. Two junior physicians were invited to refer to the dose prediction results of DESIRE for planning design. The quality of the plans from these two physicians was comparable to that of the GT, designed by a senior physician with over 10 years of experience. The encouraging result demonstrates the clinical potential of using automatic planning, which not only enhances planning quality but also improves planning stability.

Patients with NPC typically experience long-term survival. However, due to the involvement of a large number of OARs in NPC radiotherapy, effects on certain tissues, such as the brainstem, optic nerves, and larynx, largely influence patient quality of life. Thus, optimizing treatment plans to minimize OAR doses while adequately irradiating PTVs poses a challenge for treatment planners. In traditional optimization processes, planners manually set dose constraint values based on the spatial relationship between PTVs and OARs, taking into account the characteristics of different technologies. This iterative optimization strategy involves modifying parameters and applying various constraints based on optimization results to develop a plan that meets clinical requirements. However, this process is time-consuming and heavily relies on planner expertise. Furthermore, achieving further reductions in healthy tissue doses necessitates continual experimentation with new dose constraints, increasing the workload.

Feasibility DVH [21] and KBP [22, 23] are two commonly used automated planning methods but with certain limitations. For example, feasibility DVH divides the normal tissue DVH into different regions (impossible, difficult, challenging, and probable); it does not provide specific dose distribution curves, and it does not take into account the interactions of different tissue doses in addition to the healthy tissue dose distribution, which is based on the premise that 100% of PTV covers the prescribed dose. In contrast, KBP-based approaches do not adequately account for individual anatomical differences and specific clinical situations and rely on predefined models or templates based on population data. While these can provide valuable insight and general guidance for treatment planning, they may overlook nuances in a patient's anatomy or unique clinical factors that may affect treatment efficacy or toxicity outcomes. Consequently, there is a risk of creating suboptimal treatment regimens that do not meet the individual needs of each patient, which can lead to poor treatment outcomes.

Despite promising results, there are several limitations in this study. First, the framework predicts dose distributions only for VMAT plans and does not account for physician-specific preferences, such as prioritizing OAR sparing over target homogeneity. Future research could address this by training preference-aware models using data stratified by institutional protocols or physician planning styles, enabling tailored predictions for diverse clinical scenarios. Extending DESIRE to other technologies like IMRT or TOMO would require retraining with technology-specific data to accommodate technical differences. Second, the model was validated on a homogeneous NPC cohort from a single institution. While DESIRE is adaptable to multi-center data, variations in accelerator systems, TPS algorithms, and institutional constraints pose challenges. Future work will focus on expanding model validation across multiple institutions to assess its generalizability. Additionally, adapting DESIRE to other anatomical sites (e.g., lung, prostate) would require retraining with site-specific datasets. Incorporating anatomical priors, such as tumor–OAR spatial relationships, would also be essential for improving model performance across different sites. Finally, while the model predicts 3D dose distributions, translating these predictions into actionable clinical plans remains unexplored. Integrating DESIRE with automated optimization engines could bridge this gap and enable end-to-end plan generation, making it clinically actionable. This will be a key direction for future research, aiming to enhance the model's clinical utility and streamline treatment planning.

5 Conclusions

Herein, we propose DESIRE, a Dose prediction model with progrEssive feature fuSion and dIfficult Region lEarning, for NPC treatment. This method has demonstrated its capability to provide highly accurate dose predictions. Unlike previous conventional DVH-based prediction methods, our approach represents a highly promising advancement. The generated 3D dose map holds significant utility in enhancing the design of radiotherapy plans, ensuring their quality and consistency, and offering valuable guidance in the task of automatic treatment planning.

Author Contributions

Junming Jian: conceptualization, funding acquisition, methodology, resources, software, validation, and writing – original draft. Xingxing Yuan: data curation, resources, supervision, and writing – review and editing. Longfei Xu: formal analysis, software, visualization, and writing – review and editing. Changfei Gong: data curation, investigation, and writing – review and editing. Xiaochang Gong: conceptualization, formal analysis, supervision, and writing – review and editing. Yun Zhang: conceptualization, funding acquisition, project administration, resources, supervision, and writing – review and editing.

Ethics Statement

The studies involving human participants were reviewed and approved by the Ethics Committee of Jiangxi Cancer Hospital (Approval ID: 2022ky012). The study was conducted following the principles of the Declaration of Helsinki and in accordance with local statutory requirements.

Conflicts of Interest

The authors declare no conflicts of interest.