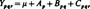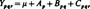Confidence Intervals on Ratios of Variance Components for the Unbalanced Two Factor Nested Model

The model considered in this article is the two-factor nested unbalanced variance component model:

for p = 1, 2, …, P; q = 1, 2, …, Q_p; and r = 1, 2, …, R_pq. The random variables Y_pqr are observable. The constant μ is an unknown parameter, and A_p, B_pq and C_pqr are (unobservable) normal and independently distributed random variables with zero means and finite variances σ²_A, σ²_B, and σ²_C, respectively. Approximate confidence intervals on ϱ_A and ϱ_B using unweighted means are derived, where The performance of these approximate confidence intervals are evaluated using computer simulation. The simulated results indicate that these proposed confidence intervals perform satisfactorily and can be used in applied problems.