1 Introduction

Survival analysis aims to model the time until the occurrence of a specific event (e.g., progression or death due to a certain disease) in dependence on a set of covariates. In clinical contexts, time-to-event data are often collected in observational studies that are prone to right censoring. Right censoring happens, for example, when patients drop out of a study or do not experience their event before the end of the observation period. In addition to a single event of interest, other event types are often recorded in observational studies and present in survival datasets. Often, the occurrence of these competing events cannot be assumed to be independent of the occurrence of the event of interest, especially if shared underlying (disease) mechanisms or shared risk factors are present.

An example would be examining kidney failure (KF) as the event of interest in patients with chronic kidney disease (CKD), while death by other causes than KF is a competing event (Hsu et al. 2017). In the German Chronic Kidney Disease (GCKD) study (Titze et al. 2015), for instance, 5217 participants with CKD are followed up annually, so data can be evaluated at the discrete time points corresponding to 1-year time intervals. One of the aims of the study is to better understand the factors underlying the progression of the disease. Potential risk factors that were collected in the study at baseline included, for example, leading kidney disease, as well as kidney function measures, such as serum creatinine, estimated glomerular filtration rate (eGFR), and U-albumin/creatinine ratio (UACR). Since CKD is a risk factor for heart failure (HF) and CKD and HF share common risk factors (Beck et al. 2015), death (e.g., from cardiovascular causes) should be considered as a competing event.

A popular approach to analyzing survival data (i.e., time to first event) in the presence of competing events is the subdistribution hazard model by Fine and Gray (1999), which extends the classical Cox proportional hazard model (Cox 1972). The Fine and Gray model introduces a subdistribution hazard function, which is a modification of the hazard function in traditional survival analysis. This function quantifies the instantaneous rate of the event of interest occurring, given that the subject has not yet experienced the event of interest until that time (assuming that the event of interest will never occur first once a competing event has already occurred (cf. Fine and Gray 1999).

As with other classical regression approaches, the subdistribution hazard model is not designed for high-dimensional data settings or complex covariate–risk relationships. In such scenarios, machine learning models such as deep survival neural networks (e.g., Giunchiglia, Nemchenko, and van der Schaar 2018; Gupta et al. 2019; Lee et al. 2018) and random survival forests (RSF) can be applied (Ishwaran et al. 2008; Schmid, Wright, and Ziegler 2016; Wright, Dankowski, and Ziegler 2017). While neural networks can be most beneficial for unstructured data, such as text and images, random forests might be advantageous for structured data exploration and for identifying important clinical covariates (Archer and Kimes 2008). Also, random forests are easy to train and require less resource-consuming hyperparameter tuning.

While numerous methods for competing events exist in classical regression, only some implementations of machine learning models for survival analysis consider competing events. In existing approaches, competing events in random forests are addressed by, for example, adapting the split rules (Ishwaran et al. 2014; Therrien and Cao 2022) or by using pseudo-value regression approaches (Mogensen and Gerds 2013). The latter method transforms the categorical event status into a continuous pseudo-value. Consequently, a random forest with regression trees is fitted instead of survival trees.

In this paper, we take a different approach for modeling competing risk data with RSF: Rather than introducing new split rules or new architectures for competing events, we transform the competing event problem into a single-event problem. This is achieved by manipulating the (input) dataset via an appropriately defined imputation scheme. More specifically, we consider three types of imputation approaches: In the first approach, the dataset is only preprocessed once before training the RSF. In the other two approaches, the dataset is adjusted directly at the tree instance of the forest: at the root node of the trees or at every node of the trees. As a consequence, well-established split rules and variable importance measures of single-event RSF can be applied. Also, the cumulative incidence function (CIF) for the event of interest can be directly calculated from the output of the single-event RSF.

The idea of using imputed censoring times instead of the observed competing event time has been applied successfully already for classical statistical modeling and neural networks: Ruan and Gray (2008) presented an imputation approach for continuous-time and semiparametric models based on Kaplan–Meier estimates. Gorgi Zadeh, Behning, and Schmid (2022) took a similar approach and proposed a method to train single-event deep neural survival networks on competing-event data, in which the unobserved censoring times of subjects with a competing event were imputed using subdistribution weights.

In this article, we describe the proposed methods and use a simulation study to evaluate their applicability and performance metrics in different situations. Finally, we report on a first application of the methods to real data obtained in the GCKD study.

2 Methods

2.4 Simulation Setup

We conducted a simulation study to investigate whether subdistribution-based imputation in the case of competing events can improve the estimation of the CIF in RSF compared to ignoring the competing events.

2.4.1 Data-Generating Mechanisms

In each simulation run, we created a set of subjects $$i = 1, \ldots, n$$, with $$n=1000$$. For each subject, we first generated a vector of 50 normally distributed covariates $$X_1, \ldots, X_{50} \sim \mathcal {N}(0,1)$$. Next, three time variables were created: a time $$T_{e_i=1}$$ for the event of interest, a time $$T_{e_i=2}$$ for the competing event, and a censoring time $$C_i$$. Afterwards, we sampled from a binary distribution with parameter $$q\in (0,1)$$ whether the event of interest ($$e_i=1$$) or the competing event ($$e_i=2$$) was observed (see below). Next, the status indicator $$\Delta _i$$ was generated as follows: the subject was censored if the censoring time was before the event time ($$\Delta _i = 0$$). If the censoring time for this subject was after the event time, the subject remained uncensored ($$\Delta _i = 1$$).

The experimental design used by Beyersmann, Allignol, and Schumacher (2011) and Berger et al. (2020) was adapted to create the event times and the censoring times. They simulated the event times $$T_{e_i=1}$$ based on a time-continuous subdistribution hazard model defined by

$$$$\begin{eqnarray*} F_1(t|X_i) &=& P(T_{cont,i} \le t, e_i = 1 \, |\, X_i) \\ &=& 1- (1-q+ q \cdot \exp (-t))^{\exp {(\eta _1(X_i}))}\text{,} \end{eqnarray*}$$$$

where $$T_{cont,i}$$ was a true underlying continuous time variable for the event of interest and $$\eta _1{(X_i})$$ was a linear predictor associated with the subdistribution time, which is described in more detail below. The parameter $$q$$ was associated with the rate of the event of interest by $$P(e_i = 1|X_i) = 1- (1-q) ^{\exp (\eta _1(X_i))}$$. The continuous event times for competing events were drawn from an exponential distribution with

$$$$\begin{equation*} T_{cont,i}| e_i = 2 \sim \text{Exp}(\lambda = \exp (\eta _2(X_i)))\,, \end{equation*}$$$$

where $$\eta _2(X_i)$$ is a linear predictor associated with the competing event time.

To discretize the continuous event times, we categorized the event times into $$k=20$$ intervals with interval borders obtained by empirical quantiles of width $$5\%$$. The empirical quantiles were pre-estimated once per parameter $$q$$ from an independent sample with 1,000,000 observations.

The discrete censoring times were generated from

$$$$\begin{equation*} P(C_i = t) = {b^{(k+1-t)}} \, \Bigg/ \, {\sum _{j=1}^{k} b^j}, \end{equation*}$$$$

where the parameter $$b$$ was associated with the overall censoring rates. As in Berger et al. (2020), the parameter $$q$$ was set to $$q \in \lbrace 0.2, 0.4, 0.8\rbrace$$ and the parameter $$b \in \lbrace 0.85, 1, 1.25 \rbrace$$, corresponding to low, medium, and high censoring rates of $$\lbrace 24\%, 47\%, 76\% \rbrace$$ (see Figures S1 and S2).

The following two covariate–risk relationships were investigated in this simulation study.

2.4.2 Setup 1: Tree-Like Covariate–Risk Relationship

To mimic a rather complex relationship between covariates and event times, we modified the linear predictor functions used in Berger et al. (2020) to have a tree-like structure as depicted in Figure 1. The covariates $$X_1, X_2, X_3, X_4, X_5$$ are associated with the event of interest, and the covariates $$X_1, X_3, X_4, X_6$$ are associated with the competing event. The tree-like predictor function for the event of interest can be written as follows:

$$$$\begin{eqnarray*} \eta _1(X_i) &= & I(X_{i1} < 0.5) \cdot (I(X_{i2} < 0) \cdot X_{i4} + I(X_{i2} \ge 0) \cdot X_{i5}) \nonumber\\ &&+\,\, I(X_{i1} \ge 0.5) \cdot (I(X_{i3} < 0) \cdot X_{i4} + I(X_{i3} \ge 0) \cdot X_{i4} \cdot X_{i5})\,, \end{eqnarray*}$$$$

where $$I(\cdot)$$ is the indicator function. The predictor for the competing event is given by

$$$$\begin{eqnarray*} \eta _2(X_i) &= & I(X_{i1} < 1) \cdot (I(X_{i1} < 0) \cdot (-X_{i4}) + I(X_{i1} \ge 0) \cdot X_{i5}) \nonumber\\ && +\,\,I(X_{i1} \ge 1) \cdot (I(X_{i3} < 0) \cdot X_{i4} + I(X_{i3} \ge 0) \cdot X_{i4} \cdot X_{i6})\,. \end{eqnarray*}$$$$

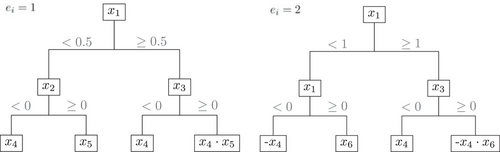
2.4.3 Setup 2: Interactions

In a second simulation setting, multiple interaction terms are included in the data-generating model. Here, the predictors for the event of interest $$e_1$$ and the competing event $$e_2$$ are specified as follows:

$$$$\begin{eqnarray*} \eta _1(X_i) &= & 2 \cdot (X_{i1} \cdot X_{i2} \cdot X_{i3} + X_{i1} \cdot X_{i4} \cdot X_{i5} + X_{i1} \cdot X_{i3} \cdot X_{i5} \nonumber\\ &&+\,\, X_{i1} \cdot X_{i3} \cdot X_{i4} + X_{i2} \cdot X_{i3} \cdot X_{i4}) \,, \end{eqnarray*}$$$$

$$$$\begin{eqnarray*} \eta _2(X_i) &= & 2 \cdot (X_{i1} \cdot X_{i3} + X_{i4} \cdot X_{i6} \cdot X_{i7} + X_{i1} \cdot X_{i4} \cdot X_{i6} \nonumber\\ &&+\,\, X_{i1} \cdot X_{i3} \cdot X_{i7} + X_{i1} \cdot X_{i3} \cdot X_{i4})\,. \end{eqnarray*}$$$$

In this setup, the covariates $$X_1, X_3$$, and $$ X_{4}$$ are associated with both events, while $$X_2$$ and $$X_5$$ are only associated with the event of interest and $$X_6$$ and $$X_7$$ are only associated with the competing event. Only the interaction term $$ X_{1} \cdot X_{3} \cdot X_{4}$$ is shared between both linear predictors. Thus, the dependency structure is similar to Setup 1, but here $$X_{7}$$ is added.

As illustrated in Table 1, the simulated datasets included event times for the event of interest as well as the competing event and censoring times. The competing event times need to be replaced by the (true or estimated) censoring times to make the simulated competing event datasets usable in the single-event RSF. After replacement, the status for the subjects with competing event was set to “censored” ($$\Delta _i =0$$). Table 2 illustrates the different imputation strategies for obtaining a reference dataset (A), a dataset preprocessed outside the RSF (B, C), and a dataset processed within the RSF (D). More specifically, the following imputation methods to estimate the CIF were compared:

• 1. Reference: If a subject $$i$$ experiences the competing event, this is replaced with the true (simulated) censoring time $$C_i$$ in the dataset. With these input data, the RSF for single events will model the true censoring rate and serves as a reference (see Table 2A).
• 2. Naive approach: Ignoring the competing event and treating the competing event time $$T_{e_i=2}$$ as if a censoring happened (see Table 2B).
• 3. Impute once (imputeOnce): Single imputed dataset before fitting the standard single-event RSF implementation (see Table 2C).
• 4. Impute in root (imputeRoot): RSF implementation with imputation in each root node, thus imputing once in each tree on all subjects available at the tree's root node (see Table 2D).
• 5. Impute in each node (imputeNode): RSF implementation with imputation in every node, thus imputing multiple times per tree on the subjects available in the respective node (see Table 2D).

TABLE 1. Example table in a simulation setting. The columns with light gray background $$ \lbrace \text{event}, T, C \rbrace$$ are produced by the data-generating mechanism but are not available during the training of the forest. The column time refers to $$\tilde{T}_i = \text{min}(T_i, C_i)$$ and the column status is defined by $$\Delta _i \cdot e_i$$.

$$i$$	Time	Status	Event	$$T$$	$$C$$	$$X_1$$	$$X_2$$	$$X_3$$	$$\ldots$$
1	15	1	1	15	18	$$-0.4411$$	$$-0.9011$$	$$-0.0924$$	$$\ldots$$
2	7	2	2	7	12	$$-1.1834$$	0.7352	$$-0.1028$$	$$\ldots$$
3	13	0	1	17	13	0.3930	$$-1.0282$$	1.2740	$$\ldots$$
4	10	2	2	10	20	0.0181	$$-1.8797$$	$$-3.5290$$	$$\ldots$$
5	3	1	1	3	14	0.7355	$$-1.0863$$	1.3222	$$\ldots$$
$$\ldots$$				$$\ldots$$

TABLE 2. Illustration of data processing: Training time and status generated from data in Table 1. (A) The event time is replaced by the simulated (true) censoring time (usually not available for training in practice). (B) The competing event time is taken as censoring time, effectively ignoring the presence of competing events. (C) The censoring time ? is replaced once before fitting the forest by an estimated censoring time (based on weights $$w_{it}$$ computed from the censoring survival function estimated from the entire training dataset). (D) The censoring time ?? is replaced repeatedly by an estimated censoring time based on weights $$w_{it}$$ computed from the censoring survival function estimated from the training data subset available in the training data subset that is available in the specific node (root node) at the random forest.

A: Simulated $$C$$			B: Naive approach			C: Impute once			D: Impute in forest
$$i$$	Time	Status	$$i$$	Time	Status	$$i$$	Time	Status	$$i$$	Time	Status
1	15	1	1	15	1	1	15	1	1	15	1
2	12	0	2	7	0	2	?	0	2	??	0
3	20	0	3	13	0	3	13	0	3	13	0
4	10	0	4	10	0	4	?	0	4	??	0
5	3	1	5	3	1	5	3	1	5	3	1

In each simulation run, we divided the dataset into a training ($$\frac{2}{3}$$) and a test set ($$\frac{1}{3}$$) before applying the methods above. Splits were stratified by the event types (event of interest, competing event, censoring). We carried out 1000 simulation runs for each combination of setup, parameters $$q$$ and $$b$$ and for each imputation method, resulting in an overall number of 90,000 simulation runs. We chose 1000 runs because this number guaranteed the width of the reference limits for the CIF (provided in Figures S6 and S7) to be smaller than 0.1 (i.e., $$2\cdot 1.96 \cdot \sqrt {0.5 \cdot (1-0.5) / 1000} = 0.0619 < 0.1$$). Apart from the described incorporated imputation approaches, the RSFs were fitted using the R package ranger from the command line interface with default parameters. This means fitting $$ntree=500$$ trees with $$mtry= 8$$ covariates selected in each node ($$mtry=\sqrt {p}$$), the log-rank split rule, sampling with replacement, and a minimal node size of 3.

3 Results

The calibration graphs in Figure 2 (simulation Setup 1) and Figure 3 (simulation setup 2) show the CIF on the test dataset that was not seen during training, averaged over 1000 simulation runs. They include nine different scenarios, that is, nine combinations of the parameters $$q$$ and $$b$$, where $$q$$ determines the rate of the event of interest, and $$b$$ affects the censoring rate.

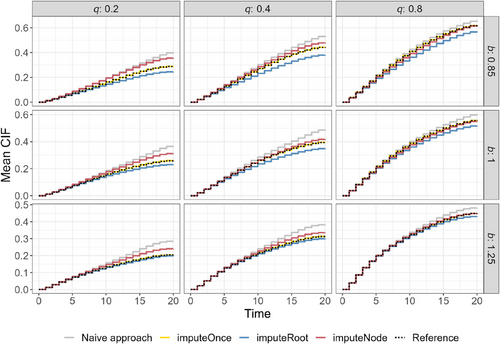
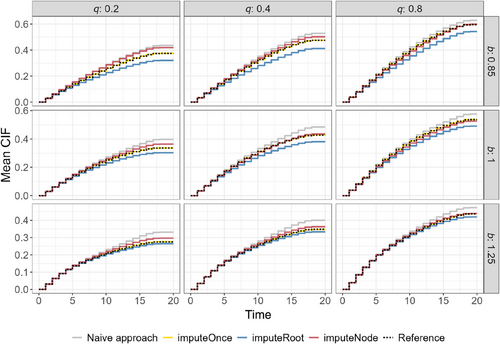
In all scenarios, all RSF architectures show similar CIF estimates for the first time points and tend to diverge for later time points. Here, the naive approach (gray lines), where competing events are treated as censoring, always shows the strongest overestimation and highest deviation from the reference method (dotted lines). The CIF of the imputeOnce approach visually overlaps with the dotted reference line that was obtained by training the single-event RSF on the simulated (true) censoring times (Reference).

The methods where the imputation is directly implemented in the nodes of the trees show the highest differences in the setting with a low censoring rate ($$b=0.85$$, first row). In all settings, the method with only one imputation in each root node tends to underestimate the CIF. In contrast, the imputation in each node tends to overestimate the CIF, especially in the scenario that corresponds to a low event-of-interest rate and a low censoring rate ($$q = 0.2, b = 0.85$$). For a better understanding of the overlap of the estimated CIF, Figures S6 and S7 provide reference limits for the estimated CIF at time points 10, 15, and 20.

Concerning the C-index and the Brier score, all methods perform similarly Tables S1–S4). The methods that do not impute directly in the random forest (imputeOnce, naive approach) performed slightly better with regard to these metrics in Setup 2. However, in Setup 1, the imputation in the root nodes of the RSF (imputeRoot) performed similarly to imputeOnce. To further gain insight on the properties of the simulation design, we divided the 1000 simulation runs into 10 batches. Using these batches, an estimate of the Monte Carlo error was calculated. The corresponding results are presented in Figures S8–S15.

In addition to the described performance measures, we calculated the permutation variable importance (VIMP) on the training dataset using the time-aggregated CHF as a marker in Harrell's C-index (cf. Ishwaran et al. 2008). Figures S16–S20 show the 10 variables with the highest mean permutation VIMP averaged over 1000 simulation runs of the training datasets in Setup 1. Note that the covariates $$X_{1}$$ to $$X_{5}$$ were included in the data-generating mechanism for the event of interest (only the covariates $$X_{4}$$ and $$X_{5}$$ were associated on a continuous level), while the covariates $$X_{1}, X_{3}, X_{4}, X_{6}$$ were associated with the competing event (see Figure 1). The variables $$X_{4}$$ and $$X_{5}$$ are indeed the two most important variables throughout for the reference, the naive approach, and imputeOnce, while mostly only $$X_5$$ was considered in the first 10 variables for imputeRoot and imputeNode in the scenarios with a low and medium rate of the event of interest ($$q \in \lbrace 0.2, 0.4\rbrace$$). In scenarios with a high rate of the event of interest ($$q=0.8)$$, $$X_2, X_3, X_4, X_5$$ were included for imputeRoot and imputeNode.

For Setup 2 (Figures S21–S25), the variables associated with the event of interest $$X_{1}$$ to $$X_{5}$$ are among the five most important variables in all scenarios for the Reference, the naive approach, and imputeOnce. In contrast, for the approaches imputeRoot and imputeNode, variables that are not associated with the event of interest get selected, especially in the scenarios with lower $$b$$. For imputeRoot and imputeNode, all of the variables $$X_{1}$$ to $$X_{5}$$ are only included in the first most important variables when the censoring rate is high ($$b = 1.25$$). For the high censoring scenario, the variables $$X_6$$ and $$X_7$$, which are associated with the competing event, are also in the top 10 most important variables.

4 Application to the GCKD Study Data

We compare the approaches described above on a complete case subset of the GCKD dataset. The dataset included 4256 participants. Of those, 412 ($$9.1\%$$) reached KF (event of interest), and 409 ($$9.6\%$$) died without reaching KF first (competing event, participants who died due to forgoing dialysis or transplantation are considered as KF). The estimated CIF and the 10 covariates with the highest VIMP can be seen in Figure 4. The CIF is lowest for the imputeOnce approach and imputeRoot. Due to the high sample size, imputeRoot and imputeOnce may lead to similar imputation results. We suspect the CIF of these two approaches to be the most realistic estimate based on the results of the simulation study, where the naive approach and imputeNode generally overestimated the CIF. Although the differences appear small, they will presumably become even more relevant with the longer observation period that can be evaluated in the future. The imputation method proposed by Ruan and Gray (2008) included analyses of multiple imputed datasets instead of a single imputation. Therefore, we performed 10 imputations of the imputeOnce method and compared the pooled results to single runs (see Table S11). In this application, however, the variability of the estimated CIF was quite low.

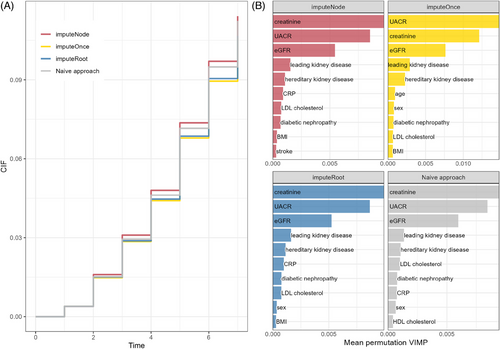
All approaches describe creatinine, UACR, eGFR, the leading CKD cause, and having a hereditary disease cause as the first five most important variables. This is followed by CRP, LDL cholesterol, and having diabetic nephropathy for imputeNode, imputeRoot, and naive approach. For imputeOnce, the demographic parameters age and sex were selected next instead of the laboratory parameters. The order of the selected covariates differs slightly between the approaches. A table containing VIMP values for all four methods can be found in Table S12. Both eGFR and UACR are reasonable covariates, as their progression is being discussed as a surrogate endpoint for progression to KF (Levey et al. 2020).

5 Conclusion

We have proposed three variants of a subdistribution-based imputation approach to handle competing risks in RSF. Our simulation study showed that the CIF is well estimated when imputation already takes place outside the forest on the training data (imputeOnce).

In survival analysis, the occurrence of competing events must be appropriately taken into account. The naive approach of considering competing events as censoring can lead to biased estimates of the CIF, although our simulation study has shown that this approach may lead to similar results in terms of C-index and IBS. Differences in the estimated CIF became apparent, especially in scenarios with a high censoring rate or a low rate of the event of interest. By including the naive approach in the simulation, we wanted to raise awareness for the proper treatment of competing events when using machine learning applications.

It should be emphasized that the naive approach estimates the cause-specific CHF of the event of interest, ignoring the hazards of the competing events. Hence, it cannot be directly transformed into the event of interest's CIF. While the CIF for the event of interest could be derived from a combination of all cause-specific hazard functions, we chose not to use this approach due to its complexity in analyzing covariate effects. Instead, we preferred the Fine and Gray method, as it provides a single (direct) effect per covariate. With random forests and other machine learning methods, having such a direct effect per covariate is a major advantage, in particular when it comes to the interpretation of measures like variable importance. Furthermore, the Fine and Gray method can reduce the computational effort, as it avoids having to fit separate machine learning models (one per cause-specific hazard). Also, note that the performance of the cause-specific hazard approach may strongly depend on the availability of sufficient numbers of observed events in the data.

A major finding of our simulation study is that imputing the estimated censoring times once before fitting the random forest (imputeOnce) essentially results in unbiased CIF estimates. Compared to imputations of the estimated censoring times in every tree node (imputeNode) or in the root node of the trees (imputeRoot), imputeOnce showed a systematically better performance with respect to the calibration graph of the CIF.

In conclusion, the proposed single-imputation strategy (imputeOnce) allows for converting the competing-risks setting into a single-event setting. All RSF features and options (split rules, variable importance measure, etc.) are immediately available for this setting, making it much more straightforward to apply RSF in the competing-risks context. Issues for future research include a comparison to other machine learning methods and other techniques for dealing with competing events in RSF. This could, for example, be done in the framework of a neutral comparison study (see, e.g., the recently published Special Collection on “Neutral Comparison Studies in Methodological Research” in Vol. 66 of Biometrical Journal).

Conflicts of Interest

The authors declare no conflicts of interest.