Journal of Applied Polymer Science
Volume 142, Issue 10 e56560
RESEARCH ARTICLE
Open Access

Relationships Between Mechanical Behavior and Structure/Properties for Macroscopically Homogeneous Porous Composites Containing Randomly Shaped Filler

Miroslav Černý, 

Corresponding Author

Miroslav Černý

Faculty of Chemistry, Brno University of Technology, Brno, Czech Republic

Correspondence:

Miroslav Černý ([email protected])

Contribution: Conceptualization (lead), Data curation (equal), Formal analysis (lead), ​Investigation (lead), Methodology (equal), Writing - original draft (lead)

Search for more papers by this author
Přemysl Menčík, 

Corresponding Author

Přemysl Menčík

Faculty of Chemistry, Brno University of Technology, Brno, Czech Republic

Central European Institute of Technology, Brno University of Technology, Brno, Czech Republic

Correspondence:

Miroslav Černý ([email protected])

Contribution: Conceptualization (supporting), Data curation (equal), Funding acquisition (lead), ​Investigation (supporting), Methodology (equal), Writing - review & editing (lead)

Search for more papers by this author
First published: 11 December 2024
https://doi.org/10.1002/app.56560

Funding: This work was supported by the Brno University of Technology [Specific University Research Grant FCH-S-23-8208].

ABSTRACT

The work focuses on researching relationships between structure/properties and mechanical behavior of porous composites. The primary data comes from tensile testing. The observed properties include elastic modulus, ultimate strength, ultimate strain, and energy need for ultimate strength achievement. The studied materials include composites based on different polyurethane matrices and one rubber filler with various filler and porosity contents. Presented work expands the possibilities of an approach based on measured data fitting by a suitable function followed by obtained parameters interpolation. The utilization of new structural parameters leads to a spatial linear function shape instead of spatial exponential. The newly introduced equation is z c  = z m  + z m · (b · p 1 + c · p 2), where z c /z m is generally labeled mechanical property value for composite/nonporous matrix, p 1/p 2 are suitable structural parameters, and b/c are fitting parameters subjected to interpolations by logarithmic function containing values of properties typical for matrices. The work focuses on studying the case of different matrices and one kind of filler. The work includes all potentially valuable interpolations for earlier mentioned properties with the most interesting results in cases of pairs p 1/p 2 containing two from three parameters: n (porosity), 1 − v m (v f  + porosity), and v f (filler volume fraction).

1 Introduction

Understanding the behavior of materials around us (including those porous) is important. The ability to predict material behavior can be the decisive parameter to its successful utilization. Materials can differ in their complexity in composition and structure. Except for the matrix, they can include fillers, reinforcement, and porosity. The term structure can also contain the shape of particles and voids, which can affect how the material will behave under loading. Description of the material behavior is usually more difficult as the material is more complex in composition and structure. This interested materials containing (except matrix) particles, voids, and mainly both of them.

First, it is necessary to mention the one-component porous materials. Many authors have endeavored to find some relationships between structure/composition and chosen mechanical properties. But the works were usually dedicated only to one material type with different degrees of porosity as porous metal [1-5], ceramics [1, 4, 6-14], polymers [1, 15], and natural materials [16]. The describing functions acquire different mathematical forms. The mathematical types of dependencies usually using some adjustable fitting parameter(s) are linear [1, 5-7, 9-13], exponential [1, 5, 6, 11, 12], power [1-4, 6, 9, 11, 12, 14, 15, 17-19], and logarithmic [5].

The more difficult situation is in the description dedicated to the more complex materials—composites. There are two approaches for describing or predicting the material behavior, which can be illustrated in the porous composites [20]. The first approach means different models [21-26] and simulations using various mathematical methods such as Fast Fourier Transform [27], finite element method [28, 29], or fractals [21]. These solutions depend on the exact physical knowledge and simplifying expectations about the composition and structure of the microscopic levels in studied materials. These expectations can vary a lot according to chosen research work. The expected limits can mean shapes of filler as granular particles [30], short fibers with cylindrical shapes [28], or circular cross-sections [27]. Forms of voids can be limited to spherical [25]. Expectations can include the exclusion of contact among pores and (short) fibers [28] or particles [21] or even the separation of one bulk phase and the open porosity by the surface phase [29]. Pores and filler are expected nano-sized in both cases [27] or only particles in the form of nanotubes or nanoparticles [23, 24]. Specific requests include the unidirectional orientation of nanofibers [27] and splitting the filler according to size distribution and location of different fractions in different domains [21]. The approach using various models and simulations predominates in the literature. It is used for the research of elastic region of loading [21, 26-28] and also for the nonlinear stress [22-24, 29, 30] with the comparisons between expected results and measured results from a provided measurement on materials.

The second approach observes the material from a macroscopic point of view concerning the properties of its components. The first part is the measurement when the measured data can be subjected to fitting by a suitable function with the following interpolation of obtained parameters to reach dependence between properties and structure/composition of the material. Work dedicated to tensile testing of porous composites containing nanofibers and describing their fracture probability according to fracture toughness and porosity by Weibull analysis [31] is an example of a macroscopic point of view.

The presented article directly follows previous work based on porous composite materials containing various polyurethane matrices with the connection of rubber filler [32, 33]. The measured data from tensile loading were subjected to fitting by spatial exponential functions represented by Equations (1 and 2) [32] and respectively (3) [33].
z c = z m ⋅ v m b ⋅ 1 − v f c (1)
z c = z m ⋅ v m b ⋅ n p c (2)
z c = z m ⋅ n p b ⋅ 1 − v f c (3)
where z c and z m are general labels for properties represented by elastic modulus (E), ultimate strength and strain (σ Fmax and ε Fmax ), and energy need for ultimate strength achievement (A Fmax ). The functions include also structural parameters v m , 1 − v f , and n p (matrix volume fraction, interspace volume—volume fraction of space among filler particles in the material, ad interspace filling—how much the matrix fulfills the interspace volume). The previous paper [32] also mentioned two other structural parameters—1 − n (solid rate of material) and n pf (matrix rate in the solid rate of material = matrix volume fraction in case of porosity neglect). These parameters are dimensionless and can have a range of values from 0 to 1. The exponents b and c are parameters ensuring the best mathematical fitting. The structural parameters are coupled into pairs because each pair is composed of two structural parameters that can describe the composition of material containing matrix, voids, and filler only together. Therefore there are three equations, including Equations (1-3), where multiplication is used between the basic members because the structural parameters v m , 1 − v f , and n p are equal to 1 for nonporous matrix and equal to 1 or lower for more complex material. The b and c parameters have the form of exponents to be distinguished for different structural parameters.
The b and c parameters have been then subjected to interpolation. The example is Equation (3) depicting interpolations in the case of elastic modulus in Equation (4):
E c = E m ⋅ n p d + e ⋅ ln E m ⋅ 1 − v f f + g ⋅ ln E m ⋅ δ (4)
where E c and E m are elastic modulus values for the composite and the nonporous matrix. δ is the OH/NCO ratio before the curing of the polyurethane matrix. δ served as an assumption of matrix polarity related to adhesion to filler (rubber in all cases). Parameters d, e, f, and g should reflect the relations between filler and matrix, but these relations were assumed only due to the utilization of only one type of filler—rubber. Therefore, previous works did not solve these relations [32, 33]. The assumption of d, e, f, and g connection to the description of filler properties or its relation to the matrix came from the idea that the parameters d, e, f, and g were the last remaining members without clear description in suggested equations and the last not described phenomenon was the description of the filler function in the composite including filler relations to the matrix. It is suitable to mention that this phenomenon consideration is quite important because it should also include a filler influence of porosity, which can be affected by filler presence, concentration, and its type in the material.
The Equations (1-3) can be simplified to obtain relationships for less complex materials. An example of the porous matrix is Equation (5):
z mn = z m ⋅ 1 − n b (5)
where z mn means property value for porous matrix, and n is dimensionless porosity (can acquire values from 0 to 1). Equation (5) occurred under different labeling and also in other sources dedicated to different mechanical properties such as elastic modulus [10, 34] and strength [1, 35]. The exponent b was presented in the mentioned works [1, 10, 34, 35] as a constant with values differing according to material type. The member 1 − n in Equation (5) is equal to n p in the case of a porous matrix, respectively v m (while 1 − v f  = 1).

To show the porous composites as recently studied topics, papers dedicated to porous composites differing by their compositions and potential applications instead of a general description of the connection between the structure and properties can be mentioned. The examples include regenerated cellulose/cross-linked poly(ethylene glycol) reaching up to 97% porosity for potential biomedical applications, packaging and sewage purification [36], properties of glass–ceramic/nanocopper [37], alloy composed of titanium, aluminum and vanadium/silver particles reaching up to 50% of porosity for biomedical applications [38], and even ceramics/epoxy resin or polycaprolactone with approximately 70% of porosity [39].

The main goal of this article is to contribute to a description of relationships between structure/composition and properties for porous-filled composites. It directly follows earlier works [32, 33] and uses the same primary data set. It should effort another insight by using complementary structural parameters to those (n p , v m , 1 − v f , etc.) used in previous articles [32, 33], because the complementary parameters introduced in this paper embody different mathematical behavior. They could then lead to new contributions in describing the behavior of porous materials. The mechanical behavior dependencies of porous composite materials are not fully known, and each contribution could stand significant.

2 Materials and Methods

2.1 Materials

This work uses the same primary dataset as previous works [32, 33], as mentioned in the introduction. The original data come from tensile testing of porous composites and the corresponding porous matrices (nonporous matrices and composites were unavailable due to the porous nature of used polyurethane matrices). All 10 used matrices were based on the same MDI (methylene-di-phenyl-di-isocyanate) pre-polymer Unixin 4223CS (Lear, Czech Republic, 6.9 wt% of isocyanate (NCO) groups, number average of molecular weight 690 g/mol, viscosity 2800 ± 500 mPa s), used the same accelerator (Lear, Czech Republic, di-butyl-tin-di-laureate, DBTL) and differed by used curing agents including castor oil (Fichema, Czech Republic), distilled water and glycerol (Penta Chemicals, Czech Republic). Some of the matrices included suitable modifying components such as linseed oil serving as a plasticizer (Fichema, Czech Republic) or inorganic fillers in powder forms of quartz (Millisil W12, Provodínské Písky, Czech Republic), calcite and iron (both of them from Pkchemie, Czech Republic, 14–16 wt% of silicon in iron) serving for the matrix stiffening to reach higher diversity in observed mechanical properties range of matrices without changes of rate or kind of curing agent. The composition of matrices in vol% is in Table 1 with the OH/NCO rate in polyurethane before curing labeled δ and designation used throughout the entire article. Particle size distributions of quartz, calcite, and iron are in Figure S1.

TABLE 1. Chemical composition of PUR samples serving as matrices for composites.
Designation PU4223 CS (vol%) Curing agent (vol%) Others (vol%) δ (−) ρ t (g cm−3) n m (%)
P99-W1 99 1 (W) — 0.68 1.10 57 ± 7
16 ± 2
P95-G5 95 5 (G) — 1.22 1.12 9.5 ± 0.7
P80-G20 80 20 (G) — 5.79 1.15 10 ± 1
P85-G5-CO10 85 5 (G) +10 (CO) — 1.55 1.05 2 ± 2
P65-CO35 65 35 (CO) — 0.87 1.04 4 ± 1
P49-CO26-LO25 49 26 (CO) 25 (LO) 0.87 1.03 1 ± 2
P33-CO17-Si50 33 17 (CO) 50 (Si) 0.87 1.85 16 ± 1
P33-CO17-Ca50 33 17 (CO) 50 (Ca) 0.87 1.86 32 ± 2
P33-CO17-Fe50 33 17 (CO) 50 (Fe) 0.87 4.04 22.6 ± 0.5
P72-G18-Ca10 72 18 (G) 10 (Ca) 5.79 1.30 16.3 ± 0.6
  • Note: Pre-polymer: PU4223 CS (P); curing agents: Water (W), glycerol (G), castor oil (CO); plasticizer: Linseed oil (LO); fillers included in matrices: SiO2 (Si), CaCO3 (Ca), Fe (Fe) [32]. Reference [33] is Reprinted by permission from Springer Nature Customer Service Centre GmbH: Springer Nature, SN Applied Sciences.
  • a Reflecting OH/NCO molar ratio.
  • b For this purpose, H2O represents two OH groups.
  • c Measured by pycnometer method.
  • d Obtained from knowledge about volume, mass, and porosity.
  • e Calculated via simple mixing equation.

The composite materials contained except matrix also rubber filler. The rubber filler was supplied and used in three fractions labeled R0–R2 (RGP Recycling, Czech Republic, higher index number means larger particles). The knife milling served for R1 and R2 fractions manufacturing. The milling with a rolling machine led to R0 manufacturing. The origin of rubber filler was the same in all cases—waste car tires. The size distributions of R0 and R1 rubber (and also of inorganic fillers) are in Figure 1 and come from laser analysis (HELOS (H2568) & RODOS). The laser analysis was not appropriate for R2 distribution due to the large dimensions of particles, and it was obtained only partially by the sieve analysis. The particle shapes of all fillers are in Figure S2 and come from scanning electron microscopy (TESCAN MIRA 3 for inorganic fillers and Carl Zeiss EVO LS 10 for rubber). The densities of all fillers were measured by a pycnometer three times. The average values are 1.18 g/cm3 for all rubber fractions, 2.65 g/cm3 for quartz, 2.68 g/cm3 for limestone, and 7.03 g/cm3 for iron.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Example of different filler content on samples based on one pair matrix/filler. The value of volume percentage is valid in case of porosity neglect. [Color figure can be viewed at wileyonlinelibrary.com]

2.2 Preparation and Testing of Samples

The preparation of samples was manual. First, liquid components were mixed (pre-polymer, curing agent(s), accelerator, and plasticizer, if it was a part of the matrix). The addition of the rubber (only one fraction in all cases) or its mixture with inorganic filler to the liquid part followed. The curing of the final blend was carried out under ambient conditions. The stainless steel molds were equipped with low-density polyethylene foil for better separation and used for the curing.

Each used filler/matrix combination underwent the density and porosity measurement. Fillers and the P99-W1 matrix (matrix labeling is in Table 1, measuring only thoroughly chosen pieces having no pores) underwent the pycnometer method (using the average from three results). The other matrices without inorganic rate were subjected to direct measurement of volume (in ethanol) and weight (8–18 g, by analytical balance) to obtain the density of porous matrices (used average from three measurements). The measurement continued with porosity observation by a confocal microscope (in optical mode). Ten figures of each matrix were obtained from the fracture surface area to get the rate of pores from each figure. The porosity and density averages gave the hypothetical nonporous matrix density value used in further calculations. The measurement of composite samples (beams) was based on measurements of dimensions (by digital caliper) and weighting. The knowledge about the theoretical (= nonporous) composition, density of partial components, and the measured density value led to the value of porosity of each composite sample according to the equation:
n = 1 − ρ ρ t = 1 − m V ∑ v it ⋅ ρ it (6)
where n is porosity, ρ is measured density, ρ t is theoretical density, m is weight, and V is the sample volume. The labels v it , and ρ it represent the volume fraction and the density of the ith component of the composite. The porosity of composites could not be accurately controlled and was measured after sample preparation. The porosity values were variable according to the filling extent and could be close to 50% of material volume and even exceed it in rare cases [32].
The beam dimensions for tensile testing were 120 mm × 24 mm × 12 mm and their values were a compromise ensuring the suppression of porosity effect to the stability of observed properties values and also adequate saving of input material due to a lot of samples (beams) including not only matrices but mainly composites based on them. Cross-head speed was 30 mm s−1. Elastic modulus came from the strain range of 0.05%–0.25%. Testing machine was ZWICK Z010 ROELL. The output included values of elastic modulus (E), ultimate strength (σ Fmax ), ultimate strain (ε Fmax ), and energy need for ultimate strength achievement (A Fmax ) calculated by the following equation:
A F max = ∑ ε n − ε n − 1 ⋅ σ n + σ n − 1 2 ; n ∈ 1 n F max (7)
where symbols σ n , σ n−1, ε n , and ε n−1 are the strength and strain values of neighboring points on the tensile curve. n Fmax represents the maximum force point. Joule per cubic meter is the basic unit of A Fmax [32, 33]. The values of properties belonging to the yield point were not present due to the missing yield point of samples.

The range of filling with rubber was 20–90 vol% with a 10% increment for all matrices. Values are valid in case of porosity neglect. This concentration set was used independently for all three rubber fractions except for the high filling of mainly lower filler fractions with combinations of some matrices. The detailed scheme of prepared and tested samples is in Figure S5. The beams creating examples with different filler contents are in Figure 1. Figure 1 also indicates the porosity rate, which usually decreases with increasing filler volume fraction. The solid filler then replaces the porous matrix. When the filler content exceeds some value differing according to matrix porosity, the matrix cannot fulfill the space between filler particles, and the porosity increases. It is usually the highest when the filler content is also highest and reaches up to 50 vol% of closed and open pores together.

2.3 Base of Calculations

Plenty of symbols are in this work. The explanations of labels are in Table S1. Table S2 contains the significance, meaning, and source for chosen parameters if they are significant for calculations. The Supporting Information section contains some schemes for a better understanding of the basic principles of this work. The scheme generally shows the data processing from the measurement to the final equations in Figure S1. Figure S2 contains the scheme of the work from rough materials through a system of prepared samples to obtain data.

This work varies in structural parameters from those used or mentioned by previous works (n p , v m , 1 − v f , 1 − n, and n pf ) [32, 33]. Although this work uses the same method to transform the composition and structure from a macroscopic point of view into relationships describing mechanical properties, it leads to different equations without collisions to those published earlier—Equations (1-3). The calculation method contains two steps too. The first is fitting ensured by the least squares method repeated many times. It leads to values of b and c parameters and the z m value. The second step is an interpolation of b and c parameters by z m and other utilizable properties of matrices in some cases. The integral area under the matrix tensile curve described by Equation (8) acquires values between 0 and 1 is significant for ultimate strength. The σ m,Fmax , ε m,Fmax , and A m,Fmax come from tables as values for nonporous matrices—Tables 4–6. δ (OH/NCO rate in the matrix before curing) is significant for elastic modulus and ultimate strength. The resulting general equation shape and description of members meaning are in Section 2.3. The basic form of equations connecting the structure/properties with behavior is the main result of this work.
S m , rel = A m , F max σ m , F max ⋅ ε m , F max (8)
The previous works [32, 33] include structural parameters equal to 1 when the matrix does not contain pores and particles. However, there is also a definition possibility of complementary structural parameters to v m , 1 − v f , n p , n pf , and 1 − n. It implies the question about their possible utilization in describing the behavior of porous composites. An example of such parameter calculation is in Equation (9):
n n = 1 − n p (9)
where n n is interspace porosity (porosity rate in the interspace = space among filler particles respectively the whole volume of the sample for unfilled samples). Analogically to Equation (9) there are defined the remaining parameters v f (filler volume fraction) from 1 − v f ; 1 − v m (volume fraction of filler and porosity) from v m ; n (porosity) from 1 − n; and n fp (filler rate in the solid rate of material = filler volume fraction in case of porosity neglect) from n pf . All complementary structural parameters can be subsequently derived in the direction from n calculated by earlier mentioned Equation (6) to n fp with knowledge of sample values of v mt (volume fraction of matrix, in case of porosity neglect) as it is in the following equations:
n n = n n + v m t 1 + n 1 − n (10)
v f = 1 − n ⋅ 1 + 1 − n n n n = 1 − n ⋅ 1 − v mt (11)
1 − v m = v f + n (12)
n fp = v f 1 − 1 − v m + v f = v f v f + v m (13)
The complementary structural parameters are generally equal to 0 in the case of the nonporous matrix. Some of these parameters are equal to 0 in the case of nonporous composite (n, n n ) and porous matrix (n fp , v f ). It means that the general multiplication between structural parameters, as occurs in Equations (1-3) mentioned in the introduction and coming from works [32, 33], cannot be used. Addition or subtraction has to replace the multiplication of structural parameters. This sign change ensures a positive non-zero value of the pair of parameters when one parameter equals 0 and the second is non-zero. It needs a relationship change between structural parameters and matrix property that creates a slope in Equation (1-3). The matrix property value should not be only the slope but also displacement in linear function, or only displacement when the slope value equals one and serves as the slope after reproaching. Splitting the matrix property to slope and displacement ensures a direct connection between matrix property and structural parameters and necessary partial separation, for example, in the case of a nonporous matrix when both structural parameters equal 0. The fitting parameter(s) need not be a power but, for example, a multiplier. This idea returns to the Equation (5). It is a simplification of Equations (1-3), where is structural parameter 1 − n valid only for porous matrices united from the n p and v m typical for more complex systems. When the 1 − n parameter is part of an analogous equation to Equation (9), it leads to n—porosity. Equation (9) could then connect not only the different structural parameters from Equations (1-3) but also different approaches of either n p , v m , and 1 − v f parameters or their complementary counterparts. Although, there is no clear mathematical role of the b parameter transformation because number 1 is now the slope, not part of the structural parameter, and only porosity should be treated (powered/multiplied) by the b parameter. Some relationships in the literature are similar to Equation (5) and could also record the utilization of complementary structural parameters n n , 1 − v m , and v f but only in the case of number 1 being outside the powered member and the porosity is powered and also multiplied by another parameter or critical porosity. They include Equation (14) from different sources [34, 40-43] and Equation (15) [12].
E mn = E m ⋅ 1 − a ⋅ n p (14)
where the a and p parameters meaning can vary according to chosen source [34, 40-43].
E mn = E m ⋅ 1 − n n c 1 J (15)
where n c is critical porosity, while the n c and J are parameters ensuring the data fitting.

3 Results and Discussion

3.1 Observation of Used Materials

The compositions and porosity of matrices are in Table 1. Measured values of mechanical properties of prepared matrices are in tables including Tables 3–6. These tables enable the comparison of the values for real porous matrices and hypothetical nonporous matrices obtained by fitting. The observed values from Tables 3–6 are elastic modulus, ultimate strength, ultimate strain, and energy need for ultimate strength achievement. Particle size distributions (obtained by laser analysis) are in Figure S1, except for the R2 rubber particle size distribution obtained by sieve analysis due to large particles. 50 wt% of R2 particles exceeded the size of 2.5 mm. The randomness of the shapes of particles is in Figure S2. The following random microstructure of composites is in Figure S3.

Composites include 10 matrices and six fillers. The calculations are focused only on different matrices. The reason is that three fillers (all inorganic) are included in matrices. The fractions of rubber filler (R0, R1, and R2) embody only low differences in particle sizes—about one mathematical order. This difference seems insufficient for study on their influence on proposed relationships. Moreover, the weak differences enabled including all rubber fractions into one filler in calculations (in each prepared sample was only one from the mentioned fractions).

3.2 Data Fitting and Numerical Relationships Between Obtained Parameters

Complementary structural parameters can be derived easily from the basic structural parameters. A suitable example is Equation (9), showing the relationship (n n  = 1 − n p ) between the interspace filling (n p ) and the interspace porosity (n n ) as its opposite. The same equation shape serves for the replacement of the basic parameters to complementary parameters in the direction shown by arrows: 1 − v f  → v f , 1 − v m  → v m , n pf  → n fp , and 1 − n → n.

Like basic structural parameters, the complementary structural parameters are in the fitting equations used in pairs. There are similarly able to describe the composition of material from two chosen parameters [32, 33].

Each complementary parameter (n n , 1 − v m , v f , n, and n pf ) is equal to zero for nonporous matrix, and its value is between 0 and 1 for more complex materials. The exceptions are the zero value for v f and n fp in the case of porous matrix and n n and n for nonporous composite. The mentioned zero values lead to different equation types using complementary structural parameters in the fitting. The spatial exponential function [32, 33], represented by Equation (16), is inappropriate because the complementary parameters p 1 or p 2 cannot be zero in it. The whole right side of the equation is then equal to zero in the case of nonporous matrix (always) and in the case of nonporous composite or porous matrix too (according to the choice of pair of complementary parameters as is described at the beginning of this paragraph). The whole equation then has no meaning because z c  ≠ 0. The right side of Equation (16) should embody non-zero values in the case of porous composite. Despite this, the equation loses its universality in the possibility of its progressive assembly while the material is becoming more complex. The suitable shape for the fitting based on complementary structural parameters is the spatial linear function described by Equation (17).
z c = z m ⋅ p 1 b ⋅ p 2 c (16)
z c = z m + z m ⋅ b ⋅ p 1 + c ⋅ p 2 (17)
where the meaning of z c , z m , b, and c corresponds to members in the Equations (1-3) respectively, Equation (16), and the remaining members are complementary structural parameters. Parameters p 1 and p 2 are signs in their general form. The mathematical relationships among equation members vary from those in Equations (1-3). Fitting members (b, c) are multipliers (instead of exponents), and between structural parameters is plus instead of multiplication. The value of the nonporous matrix property is not only the slope but moreover a displacement from the diagram beginning on the positive part of y-axis. The nonporous matrix property (elastic modulus, etc.) retains the slope meaning because of the necessity to join the matrix mechanical behavior directly with the composition of more complex materials.
There is no problem with zero values of complementary parameters p 1 and p 2 for nonporous matrix—Equation (17) changes its shape to z c  = z m  + 0, which is existing equality (value for nonporous matrix in both sides of the equation). Moreover, there is no problem with zero values of parameters p 1 and p 2 for nonporous composite and porous matrix—one of the parameters can be zero, and the right side is still not equal to zero or only z m . There are exceptions shown in Table 2, but Equation (17) combined with suitable pairs of complementary parameters has universality in progressive assembly while the material is becoming more complex. The overview of the suitability of structural parameter pairs for fitting Equation (17) is in Table 2. The studied types of Equation (17) include Equations (18-23) and come from the suitability of complementary parameters shown in this table.
z c = z m + z m ⋅ b ⋅ n fp + c ⋅ n n (18)
z c = z m + z m ⋅ b ⋅ 1 − v m + c ⋅ n n (19)
z c = z m + z m ⋅ b ⋅ n n + c ⋅ v f (20)
z c = z m + z m ⋅ b ⋅ 1 − v m + c ⋅ v f (21)
z c = z m + z m ⋅ b ⋅ n + c ⋅ 1 − v m (22)
z c = z m + z m ⋅ b ⋅ n + c ⋅ v f (23)
TABLE 2. Suitability of all possible 10 pairs of structural parameters for research.
Parameter Suitability or reason for exclusion
n + n n Nonporous composite: n + n n  = 0
n fp  + v f Porous matrix: n fp  + v f  = 0
n fp  + n; n fp  + (1 − v m ) First fitting: low R 2
(1 − v m ) + n n ; n n  + v f ; n fp  + n n Slopes values differing according to the used pair of structural parameters
(1 − v m ) + n; n + v f ; n + (1 − v m ) Repetition of slope values
  • Note: Unsuitable pairs were excluded immediately after finding some insufficiency without the whole search for their complex behavior.
There was found no exact mathematical reason why b and c have the form of multipliers of the structural parameters and not as their exponents. The equation form choice was according to the ability to fit the measured data. The general shape of the function is in Equations (24 and 25). These equations depict the possible mathematical treatment of Equation (17):
z c = z m + z m ⋅ b ⋅ p 1 + c ⋅ p 2 = z m − z m ⋅ − b ⋅ p 1 − c ⋅ p 2 (24)
z c = z m ⋅ 1 + b ⋅ p 1 + c ⋅ p 2 = z m ⋅ 1 − − b ⋅ p 1 + − c ⋅ p 2 (25)

It is necessary to add that the b and c parameters can acquire positive or negative values in both cases of slope sign. It means that, for example, a combination of a negative slope with two positive parameter values, two negative parameter values, or one positive and one negative parameter value according to the chosen fitting example (property and matrix, explained below). When the slope changes its sign, the signs of parameter values also change. It is only a mathematical treatment shown by Equation (24).

The left-placed version of Equation (24) corresponds to Equation (17) which represents the only equation shape in this work. Equation (25) corresponds to Equation (24) after mathematical deriving by pointing the z m value out.

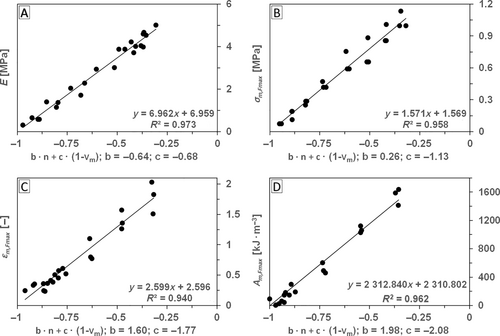
The data fitting used the form of an adjustment of the b and c values. It was provided separately for each chosen property, and a set of composites based on one from the used matrices. The filler was the same in all cases. Fitting was used for one property and one matrix in the composite as shown in Figure 2. The fitting was concerned with reaching the highest coefficient of determination (R 2) value. All combinations of b and c values embodying the highest R 2 value for separate fitting created a trend with a linear dependence of c on b. On that line, there were two combinations of b and c parameter values differing only by the b and c mathematical sign ensuring the same absolute value of slope and displacement. The resulting slope value then varies only in the mathematical positivity/negativity of its value and the result dependence, as depicted in Figure 2 and Equations (17-23) for the case of the positive slope. The results giving the positive slope were the only ones included in the following work. Figure 2 shows the typical difference between slope and displacement caused by the method used (usually the third valid numeral). The fitting results (for chosen structural pairs) in the form of displacements values are in Table 3 for E, Table 4 for σ m,Fmax , Table 5 for ε m,Fmax , and Table 6 for A m,Fmax . There are also the property values for real porous matrices and porosity to estimate obtained results (the accurate comparison is unsuitable due to the absence of real nonporous matrices).

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
A linear fitting example of observed mechanical properties including E (A), σ Fmax (B), ε Fmax (C), and A Fmax (D) of porous composites based on P72-G18-Ca10 matrix and different fractions of rubber fitted according to expression b · n + c · (1 − v m ) leading to Equation (22). The other linear fittings leading to Equations (18-21) and (23) are in the same way.
TABLE 3. Comparison of elastic modulus values of individual matrices between measured values of real porous matrices with mentioned porosities [32, 33] and values obtained by Equations (18-23) represented by given pairs of structural parameters.
Matrix designation Measured values (porous matrices) E (MPa): fitted values of (nonporous matrices), if the structural parameters p 1 and p 2 are
n (%) E (MPa) n fp ; n n 1 − v m ; n n n n ; v f 1 − v m ; v f n; v f n; 1 − v m
P99-W1 57 ± 7 1.4 ± 0.3 6.65 4.69 5.98 8.85 8.78 8.80
P99-W1 16 ± 2 4.1 ± 0.1
P95-G5 9.5 ± 0.7 13 ± 2 11.38 16.10 12.52 14.94 15.13 14.99
P80-G20 10 ± 1 4.8 ± 0.3 4.65 5.31 4.87 5.54 5.54 5.54
P85-G5-CO10 2 ± 2 2.3 ± 0.3 2.15 1.69 1.97 2.49 2.50 2.49
P65-CO35 4 ± 1 1.6 ± 0.4 2.22 1.63 2.00 2.58 2.60 2.61
P49-CO26-LO25 1 ± 2 1.1 ± 0.03 1.07 0.81 0.96 1.22 1.25 1.24
P33-CO17-Si50 16 ± 1 9 ± 1 12.39 13.12 12.47 15.15 15.14 15.17
P33-CO17-Ca50 32 ± 2 4.9 ± 0.5 10.20 11.72 10.55 12.90 12.90 12.90
P33-CO17-Fe50 22.6 ± 0.5 9.1 ± 0.6 14.96 16.66 15.46 18.41 18.41 18.44
P72-G18-Ca10 16.3 ± 0.6 7.4 ± 0.8 5.83 6.51 6.03 6.96 6.94 6.96
  • a Depicted in Figure 2.
TABLE 4. Comparison of ultimate strength values of individual matrices between measured values of real porous matrices with mentioned porosities [32, 33] and values obtained by Equations (18-23) represented by given pairs of structural parameters.
Matrix designation Measured values (porous matrices) σ Fmax (MPa): fitted values of (nonporous matrices), if the structural parameters p 1 and p 2 are
n (%) σ Fmax (MPa) n fp ; n n 1 − v m ; n n n n ; v f 1 − v m ; v f n; v f n; 1 − v m
P99-W1 57 ± 7 0.56 ± 0.05 2.03 2.23 2.06 2.90 2.87 2.89
P99-W1 16 ± 2 2.7 ± 0.3
P95-G5 9.5 ± 0.7 4.7 ± 0.1 2.76 4.33 3.26 3.71 3.74 3.68
P80-G20 10 ± 1 1.75 ± 0.08 1.25 1.46 1.32 1.45 1.45 1.45
P85-G5-CO10 2 ± 2 1.24 ± 0.04 1.01 1.02 1.02 1.15 1.14 1.14
P65-CO35 4 ± 1 0.42 ± 0.03 0.47 0.37 0.43 0.54 0.54 0.54
P49-CO26-LO25 1 ± 2 0.4 ± 0.03 0.30 0.25 0.27 0.32 0.32 0.32
P33-CO17-Si50 16 ± 1 2.2 ± 0.3 2.57 3.32 2.81 3.22 3.22 3.22
P33-CO17-Ca50 32 ± 2 0.7 ± 0.04 1.14 1.21 1.16 1.41 1.41 1.41
P33-CO17-Fe50 22.6 ± 0.5 1.09 ± 0.09 1.37 1.55 1.44 1.68 1.68 1.68
P72-G18-Ca10 16.3 ± 0.6 1.93 ± 0.06 1.33 1.61 1.43 1.57 1.57 1.57
  • a Depicted in Figure 2.
TABLE 5. Comparison of ultimate strain values of individual matrices between measured values of real porous matrices with mentioned porosities [32, 33] and values obtained by Equations (18-23) represented by given pairs of structural parameters.
Matrix designation Measured values (porous matrices) ε Fmax (%): fitted values of (nonporous matrices), if the structural parameters p 1 and p 2 are
n (%) ε Fmax (%) n fp ; n n 1 − v m ; n n n n ; v f 1 − v m ; v f n; v f n; 1 − v m
P99-W1 57 ± 7 94 ± 9 114 167 130 153 151 153
P99-W1 16 ± 2 82 ± 12
P95-G5 9.5 ± 0.7 140 ± 40 99 130 111 124 125 124
P80-G20 10 ± 1 340 ± 20 328 462 374 367 367 367
P85-G5-CO10 2 ± 2 100 ± 4 141 165 149 154 154 154
P65-CO35 4 ± 1 39 ± 4 40 36 39 41 41 41
P49-CO26-LO25 1 ± 2 68 ± 8 52 50 51 53 53 52
P33-CO17-Si50 16 ± 1 22 ± 1 22 23 22 23 23 23
P33-CO17-Ca50 32 ± 2 20 ± 1 19 18 18 19 19 19
P33-CO17-Fe50 22.6 ± 0.5 13 ± 1 14 15 15 14 14 14
P72-G18-Ca10 16.3 ± 0.6 260 ± 30 224 315 255 260 260 260
  • a Depicted in Figure 2.
TABLE 6. Comparison of energy need for ultimate strength achievement values of individual matrices between measured values of real porous matrices with mentioned porosities [32, 33] and values obtained by Equations (18-23) represented by given pairs of structural parameters.
Matrix designation Measured values (porous matrices) A Fmax (kJ m−3): fitted values of (nonporous matrices), if the structural parameters p 1 and p 2 are
n (%) A Fmax (kJ m−3) n fp ; n n 1 − v m ; n n n n ; v f 1 − v m ; v f n; v f n; 1 − v m
P99-W1 57 ± 7 321 ± 14 881 1243 974 1315 1309 1318
P99-W1 16 ± 2 1400 ± 400
P95-G5 9.5 ± 0.7 4100 ± 700 1423 2478 1757 1965 1986 1946
P80-G20 10 ± 1 3700 ± 300 2450 3593 2841 2749 2748 2748
P85-G5-CO10 2 ± 2 700 ± 50 733 895 793 826 825 825
P65-CO35 4 ± 1 69 ± 6 132 92 119 147 149 150
P49-CO26-LO25 1 ± 2 90 ± 8 86 81 84 93 94 93
P33-CO17-Si50 16 ± 1 210 ± 40 258 325 279 325 325 325
P33-CO17-Ca50 32 ± 2 69 ± 9 114 128 116 147 146 147
P33-CO17-Fe50 22.6 ± 0.5 70 ± 10 105 126 112 131 131 131
P72-G18-Ca10 16.3 ± 0.6 3700 ± 300 1958 2942 2299 2311 2311 2311
  • a Depicted in Figure 2.
Ten potentially suitable pairs of structure parameters are already mentioned in Table 2. Only six pairs corresponding to Equations (18-23) were used for fitting (n fp  + n n , n n  + 1 − v m , n n  + v f , 1 − v m  + v f , n + 1 − v m , and n + v f ). The process leads to interesting relationships among the b and c parameters. There were found dependencies in each equation in the form of linear dependence:
c = x + y ⋅ b → z c = z m + z m b ⋅ p 1 + x + y ⋅ b ⋅ p 2 (26)
where x is displacement and y is the slope of c dependence on b. This dependence is then installed instead of the c multiplier to Equation (17), as shown in the following part of Equation (26). The obtained dependencies for each proven combination of structural parameters and observed properties are in Table 7.
TABLE 7. Dependencies of structural parameters c and b in the form of c = f(b) in Equations (18-23) in cases of different properties fitting (E, σ Fmax , ε Fmax respectively A Fmax ) with the attached coefficient of determination (R 2) values.
Property p 1 + p 2 (in b · p 1 + c · p 2) Eq. c = f(b) c = f(b); R 2
E n fp  + n n (18) c = − 0.864 · b − 1.101 0.994
(1 − v m ) + n n (19) c = − 0.962 · b − 1.061 0.998
n n  + v f (20) c = − 2.431 · b − 2.646 0.980
(1 − v m ) + v f (21) c = − 2.529 · b − 2.323 0.995
n + (1 − v m ) (22) c = − 0.574 · b − 1.097 0.997
n + v f (23) c = − 1.333 · b − 2.550 0.983
σ Fmax n fp  + n n (18) c = − 0.870 · b − 1.074 0.978
(1 − v m ) + n n (19) c = − 0.991 · b − 1.047 0.993
n n  + v f (20) c = − 2.301 · b − 2.483 0.939
(1 − v m ) + v f (21) c = − 2.295 · b − 2.410 0.961
n + (1 − v m ) (22) c = − 0.580 · b − 1.081 0.990
n + v f (23) c = − 1.314 · b − 2.483 0.940
ε Fmax n fp  + n n (18) c = − 0.603 · b − 0.282 0.872
(1 − v m ) + n n (19) c = − 0.611 · b − 0.249 0.895
n n  + v f (20) — —
(1 − v m ) + v f (21) — —
n + (1 − v m ) (22) c = − 0.819 · b − 0.414 0.876
n + vf (23) — —
A Fmax n fp  + n n (18) c = − 0.960 · b − 1.151 0.986
(1 − v m ) + n n (19) c = − 1.020 · b − 1.091 0.995
n n  + v f (20) c = − 1.908 · b − 2.201 0.946
(1 − v m ) + v f (21) c = − 2.057 · b − 2.223 0.978
n + (1 − v m ) (22) c = − 0.523 · b − 1.065 0.985
n + v f (23) c = − 1.062 · b − 2.199 0.936
  • a There are also shown pairs of structural parameters in the Equations (18-23) generally shaped as  z c  = z m  + z m · (b · p 1 + c · p 2).
Moreover, there are linear dependencies of b and c multipliers across different Equations (18-23) when all relationships belong to one observed property. The equation can acquire more forms:
b ; c = f b ; c ; b + c ; b − c (27)
where b or c on the left side belongs to one equation from Equations (18-23), and the random multiplier or sum of multipliers on the right side belongs to another random equation from Equations (18-23). Both multipliers come from one equation from (Equations 18-23) if the sum is on the ride side of Equation (27). Very high values of coefficient of determination R 2 were observed in dependencies of b/c on b/c created from b and c coming from E fitting (nearly 1). The variously worse results occur after the fitting in the cases of the other properties. If there is dependence generally of one multiplier on the sum of multipliers, any dependencies are very rare, but some examples exist. The result is plenty of more or less good linear dependencies. However, some cases are even without any found relationship. There is no reason to show them instead of the dependencies of b on c closed in certain equations depicted in Table 7. However, there is a reason to show some exceptional equations from the plenty of relationships. The chosen relationships have the simple shape y = x or y = −x, and their R 2 equals 1 or it is only a little lower. The very significant thing is that the chosen relationships connect all of the b and c members of only three equations including Equations (21-23) mathematically together, and there it is no other exact relationships coming from Equations (18-20). The linear dependencies of b and c across Equations (21-23) work after fitting in cases of all properties by the same mean. The better way to express most of these relationships is by simplifying the material to a nonporous composite (n; n n  = 0, remaining parameters reduced to v f ) or porous matrix (n fp ; v f  = 0, remaining parameters reduced to n). These expressions (and the addition of relationships without the ability to be shown by material with reduced composition) of b and c connections are in Table 8. This table shows the close connection among the Equations (21-23). Their close relationship can be seen even in Tables 3–6, with very similar values of displacements coming from fitting (nearly equal).
TABLE 8. The mathematical behavior of pairs of structural parameters and their multipliers coming from the Equations (21-23) in simplified situations of less complex materials.
Porous composite (the examples of fitting results of Equations (21-23)) from up to down
σ c,Fmax (MPa) = 3.71 MPa + 3.69 MPa · (− 0.91 · (1 − v m ) − 0.42 · v f )
σ c,Fmax (MPa) = 3.68 MPa + 3.68 MPa · (0.35 · n − 1.29 · (1 − v m ))
σ c,Fmax (MPa) = 3.74 MPa + 3.73 MPa · (−0.91 · n − 1.34 · v f )
Multiplied parameters Mathem. treatment Multipliers behavior (Eq.) Notice
Hypothetical nonporous composite
−0.91 · (1-v m ) − 0.42 · v f −1.33 · v f b + c (21) = c (22) = c (23) 1 − v m  = v f
0.35 · n − 1.29 · (1 − v m ) −1.29 · v f c (22) = c (23) = b + c (21) 1 − v m  = v f , n = 0
−0.91 · n − 1.34 · v f −1.34 · v f c (23) = b + c (21) = c (22) n = 0
Porous matrix
−0.91 · (1 − v m ) − 0.42 · v f −0.91 · n b (21) = b + c (22) = b (23) 1 − v m  = n, v f  = 0
0.35 · n − 1.29 · (1 − v m ) −0.94 · n b + c (22) = b (23) = b (21) 1 − v m  = n
−0.91 · n − 1.34 · v f −0.91 · n b (23) = b (21) = b + c (22) v f  = 0
Further relationships found between b and c multipliers
c (21) = −b (22) = b − c (23)
  • Note: The data fittings connecting the composites based on the P95-G5 matrix and corresponding ultimate strength values serve as an example.

3.3 Interpolation of b and c Parameters Obtained by Fitting

The b and c parameters in each equation or across different equations have mathematical connections, but this is not important without further interpolations giving them clear meaning. The work led to the finding of dependencies of b and c on matrix properties only because only one type of filler was used (instead of 10 various matrices). The interpolation possibilities differ according to the observed property. This result should depend on the relationships between b and c coming from fitting. The graphical examples of interpolation are in figures including Figures 3-8. All interpolation results are in tables including Tables 9–12 that serve as interpolation overviews for separated observed properties. Two interpolation possibilities are for the b and c parameters if the observed property is elastic modulus. The interpolation by expression E m · δ gives the generally higher R 2 than only the E m (elastic modulus value of matrix) independently of the choice of structural parameters pair. The resulting interpolation is shown by Equation (28) if the structural parameters are written generally as p 1 and p 2, and the choice is according to the value of R 2.
E c = E m + E m ⋅ d + e ⋅ ln E m ⋅ δ ⋅ p 1 + f + g ⋅ ln E m ⋅ δ ⋅ p 2 (28)
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Example of b (A, C) and c (B, D) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for elastic modulus according to E m (A, B) and E m · δ (C, D), where E m values are from Table 3 and δ values are from Table 1. [Color figure can be viewed at wileyonlinelibrary.com]
TABLE 9. Interpolation possibilities of b and c parameters from Equations (18-23) with general shape z c  = z m  + z m · (b · p 1 + c · p 2) for elastic modulus according to E m and E m · δ, where E m [MPa] values are from Table 3 and δ values from Table 1.
Eq. p 1 + p 2 b = f(x); x = E m · δ R 2 c = f(x); x = E m · δ R 2
(18) n fp  + n n b = −1.130 · ln x + 2.284 0.795 c = 0.983 · ln x − 3.535 0.786
(19) (1 − v m ) + n n b = − 1.359 · ln x + 3.346 0.879 c = 1.311 · ln x − 4.287 0.881
(20) n n  + v f b = 0.451 · ln x − 2.203 0.822 c = −1.112 · ln x + 2.742 0.829
(21) (1 − v m ) + v f b = 0.638 · ln x − 3.315 0.741 c = −1.505 · ln x + 5.224 0.760
(22) n + (1 − v m ) b = 1.465 · ln x − 5.112 0.763 c = − 0.847 · ln x + 1.849 0.772
(23) n + v f b = 0.611 · ln x − 3.244 0.741 c = − 0.839 · ln x + 1.827 0.772
Eq. p 1 + p 2 b = f(x); x = E m R 2 c = f(x); x = E m R 2
(18) n fp  + n n b = −1.388 · ln x + 2.912 0.711 c = 1.144 · ln x − 3.523 0.642
(19) (1 − v m ) + n n b = −1.679 · ln x + 3.457 0.840 c = 1.588 · ln x − 4.342 0.810
(20) n n  + v f b = −0.516 · ln x − 2.173 0.647 c = −1.378 · ln x + 2.845 0.767
(21) (1 − v m ) + v f b = 0.761 · ln x − 3.350 0.658 c = −1.847 · ln x + 5.404 0.715
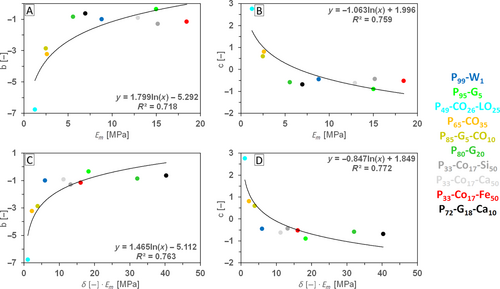
(22) n + (1 − v m ) b = 1.799 · ln x − 5.292 0.718 c = −1.063 · ln x + 1.996 0.759
(23) n + v f b = −0.727 · ln x − 3.274 0.653 c = −1.053 · ln x + 1.972 0.757
  • a Dependencies depicted in Figure 3.

All interpolation possibilities of b and c parameters in the case of E are in Table 9 for all fitting Equations (18-23). The examples of interpolations coming from Equation (22) are in Figure 3. All interpolations lead to logarithmic functions.

Four interpolation types of the b and c parameters are possible if the observed property is the ultimate strength. Most simple interpolation done only by σ m,Fmax gives the lowest R 2 values. The multiplication of σ m,Fmax by δ or S m,rel , or using both extra variables δ (as a multiplier) or S m,rel (as a divisor) can improve the interpolation. The interpolation by expression σ m,Fmax · δ/S m,rel gives mostly the highest R 2 (with some exceptions of interpolation by σ m,Fmax · δ and σ m,Fmax · S m,rel ). S m,rel values were obtained from Equation (8). Values for S m,rel calculation in Equation (8), including σ m,Fmax , ε m,Fmax , and A m,Fmax , were from Tables 4–6. Each b and c parameter interpolation (from any equation) is independent. The resulting interpolation equations then acquire a lot of types due to the many possibilities of their interpolation. Therefore, only the most successful cases of Equations (18-23) are shown. The most common form is (structural parameters are written generally as p 1 and p 2):
σ c , F max = σ m , F max + σ m , F max ⋅ d + e ⋅ ln σ m , F max ⋅ δ S m , rel ⋅ p 1 + f + g ⋅ ln σ m , F max ⋅ δ S m , rel ⋅ p 2 (29)
if p 1 = 1 − v m and p 2 = v f , it is the best some other interpolation:
b = d + e ⋅ ln σ m , F max ⋅ δ S m , rel ; c = f + g ⋅ ln σ m , F max ⋅ δ (30)
if p 1 = n and p 2 = 1 − v m , it is the best some other interpolation:
b = d + e ⋅ ln σ m , F max ⋅ δ ; c = f + g ⋅ ln σ m , F max ⋅ S m , rel (31)
and if p 1 = n and p 2 = v f , it is the best some other interpolation:
b = d + e ⋅ ln σ m , F max ⋅ δ S m , rel ; c = f + g ⋅ ln σ m , F max ⋅ S m , rel (32)

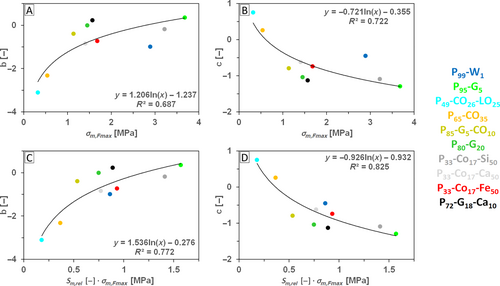
Equations (30-32) embody only a weak advantage against the interpolation presented by Equation (29). The interpolation possibilities overview if the observed property is the ultimate strength is in Table 10. The graphical overview for the case if the structural parameters are n and 1 − v m is in Figures 4 and 5.

TABLE 10. Interpolation possibilities of b and c parameters from Equations (18-23) with general shape z c  = z m  + z m · (b · p 1 + c · p 2) for ultimate strength according to σ m,Fmax , σ m,Fmax · S m,rel , σ m,Fmax · δ and σ m,Fmax · δ/S m,rel , where σ m,Fmax [MPa] values are from Table 4, δ values from Table 1 and S m,rel from Equation (8).
Eq. p 1 + p 2 b = f(x); x = σ m,Fmax R 2 c = f(x); x = σ m,Fmax R 2
(18) n fp  + n n b = −0.949 · ln x − 0.225 0.668 c = 0.763 · ln x − 0.868 0.559
(19) (1 − v m ) + n n b = −1.088 · ln x − 0.026 0.817 c = 1.080 · ln x − 1.022 0.816
(20) n n  + v f b = −0.361 · ln x − 1.004 0.603 c = −0.976 · ln x + 0.145 0.781
(21) (1 − v m ) + v f b = 0.526 · ln x − 1.592 0.673 c = −1.246 · ln x + 1.258 0.689
(22) n + (1 − v m ) b = 1.206 · ln x − 1.237 0.687 c = −0.721 · ln x − 0.355 0.721
(23) n + v f b = 0.514 · ln x − 1.579 0.664 c = −0.774 · ln x − 0.372 0.820
Eq. p 1 + p 2 b = f(x); x = σ m,Fmax · S m,rel R 2 c = f(x); x = σ m,Fmax · S m,rel R 2
(18) n fp  + n n b = −1.145 · ln x − 0.902 0.778 c = 0.938 · ln x − 0.316 0.675
(19) (1 − v m ) + n n b = −1.350 · ln x − 0.840 0.860 c = 1.344 · ln x − 0.213 0.863
(20) n n  + v f b = 0.457 · ln x − 0.736 0.698 c = −1.207 · ln x − 0.858 0.864
(21) (1 − v m ) + v f b = 0.635 · ln x − 1.182 0.694 c = −1.571 · ln x + 0.264 0.775
(22) n + (1 − v m ) b = 1.536 · ln x − 0.276 0.772 c = −0.926 · ln x − 0.932 0.825
(23) n + v f b = 0.620 · ln x − 1.181 0.681 c = −0.946 · ln x − 0.976 0.862
Eq. p1 + p2 b = f(x); x = σ m,Fmax · δ R 2 c = f(x); x = σ m,Fmax · δ R 2
(18) n fp  + n n b = −0.680 · ln x − 0.062 0.848 c = 0.607 · ln x − 1.027 0.872
(19) (1 − v m ) + n n b = −0.772 · ln x + 0.129 0.834 c = 0.784 · ln x − 1.185 0.870
(20) n n  + v f b = 0.296 · ln x − 1.081 0.915 c = −0.676 · ln x + 0.003 0.848
(21) (1 − v m ) + v f b = 0.411 · ln x − 1.677 0.885 c = −0.951 · ln x + 1.433 0.862
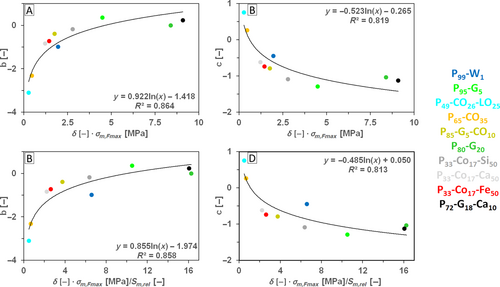
(22) n + (1 − v m ) b = 0.922 · ln x − 1.418 0.864 c = −0.523 · ln x − 0.265 0.819
(23) n + v f b = 0.406 · ln x − 1.655 0.892 c = −0.529 · ln x − 0.298 0.824
Eq. p1 + p2 b = f(x); x = σ m,Fmax · δ/S m,rel R 2 c = f(x); x = σ m,Fmax · δ/S m,rel R 2
(18) n fp  + n n b = −0.682 · ln x + 0.362 0.867 c = 0.602 · ln x − 1.399 0.873
(19) (1 − v m ) + n n b = −0.729 · ln x + 0.580 0.870 c = 0.737 · ln x + 1.640 0.901
(20) n n  + v f b = 0.283 · ln x − 1.253 0.917 c = −0.660 · ln x + 0.410 0.884
(21) (1 − v m ) + v f b = 0.391 · ln x − 1.940 0.914 c = −0.885 · ln x + 2.026 0.856
(22) n + (1 − v m ) b = 0.855 · ln x − 1.974 0.858 c = −0.485 · ln x + 0.050 0.813
(23) n + v f b = 0.385 · ln x − 1.922 0.922 c = −0.505 · ln x + 0.041 0.861
  • a Dependencies depicted in Figure 4.
  • b Dependencies depicted in Figure 5.
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Example of b (A, C) and c (B, D) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for ultimate strength according to σ m,Fmax (A, B) and σ m,Fmax · S m,rel (C, D), where σ m,Fmax values are from Table 4 and S m,rel values from Equation (8). [Color figure can be viewed at wileyonlinelibrary.com]
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Example of b (A, C) and c (B, D) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for ultimate strength according to σ m,Fmax · δ (A, B) and σ m,Fmax · δ/S m,rel (C, D), where σ m,Fmax values are from Table 4, δ values are from Table 1 and S m,rel values from Equation (8). [Color figure can be viewed at wileyonlinelibrary.com]
Three interpolation types of the b and c parameters are possible if the observed property is the ultimate strain. The interpolation by expression ε m,Fmax · δ gives mostly the highest R2 with some exceptions of interpolation by δ. The interpolation only according to simple ε m,Fmax is possible and is more appropriate than δ in many cases (not all), while it is also worse than ε m,Fmax · δ. Each b and c parameter interpolation (from any equation) is independent. The resulting interpolation equations then can acquire a lot of types due to many possibilities of how to interpolate them. Therefore, only the most successful cases of Equations (18-23) are shown. The most appropriate forms are (structural parameters are written generally as p 1 and p 2):
ε c , F max = ε m , F max + ε m , F max ⋅ d + e ⋅ ln ε m , F max ⋅ δ ⋅ p 1 + f + g ⋅ ln ε m , F max ⋅ δ ⋅ p 2 (33)
if the pair of structural parameters p 1 + p 2 is (1 − v m ) + n n or n + 1 − v m .
ε c , F max = ε m , F max + ε m , F max ⋅ d + e ⋅ ln ε m , F max ⋅ δ ⋅ p 1 + f + g ⋅ ln δ ⋅ p 2 (34)
if the pair of structural parameters p 1 + p 2 is n fp  + n n .
ε c , F max = ε m , F max + ε m , F max ⋅ d + e ⋅ ln δ ⋅ p 1 + f + g ⋅ ln ε m , F max ⋅ δ ⋅ p 2 (35)
if the pair of structural parameters p 1 + p 2 is n n  + v f , (1 − v m ) + v f or n + v f . The dependence c = f(ε m,Fmax ) is also good in these cases. Functions coming from interpolation are in Table 11, serving as an interpolation overview for interpolation related to ε Fmax . The possibilities of interpolation if the pair of structural parameters is n + 1 − v m are in Figure 6.
TABLE 11. Interpolation possibilities of b and c parameters from Equations (18-23) with general shape z c  = z m  + z m · (b · p 1 + c · p 2) for ultimate strain according to ε m,Fmax , ε m,Fmax · δ and δ, where σ m,Fmax [MPa] values are from Table 5 and δ values from Table 1.
Eq. p 1 + p 2 b = f(x); x = ε m,Fmax R 2 c = f(x); x = ε m,Fmax R 2
(18) n fp  + n n b = −0.822 · ln x − 1.102 0.860 c = 0.424 · ln x + 0.353 0.550
(19) (1 − v m ) + n n b = −0.676 · ln x + 0.908 0.889 c = 0.372 · ln x + 0.294 0.647
(20) n n  + v f not found — c = −0.696 · ln x − 0.942 0.885
(21) (1 − v m ) + v f not found — c = −0.647 · ln x − 0.647 0.667
(22) n + (1 − v m ) b = 0.650 · ln x + 0.657 0.681 c = −0.666 · ln x − 0.996 0.932
(23) n + v f not found — c = −0.666 · ln x − 0.996 0.933
Eq. p 1 + p 2 b = f(x); x = εm,Fmax · δ R 2 c = f(x); x = ε m,Fmax · δ R 2
(18) n fp  + n n b = −0.525 · ln x − 0.815 0.928 c = 0.297 · ln x + 0.207 0.714
(19) (1 − v m ) + n n b = −0.441 · ln x − 0.706 0.903 c = 0.262 · ln x + 0.182 0.765
(20) n n  + v f b = 0.072 · ln x − 0.294 0.446 c = −0.447 · ln x − 0.712 0.931
(21) (1 − v m ) + v f b = 0.104 · ln x − 0.478 0.514 c = −0.448 · ln x − 0.444 0.793
(22) n + (1 − v m ) b = 0.450 · ln x + 0.452 0.809 c = −0.425 · ln x − 0.786 0.939
(23) n + v f b = 0.102 · ln x − 0.470 0.550 c = −0.424 · ln x − 0.786 0.936
Eq. p 1 + p 2 b = f(x); x = δ R 2 c = f(x); x = δ R 2
(18) n fp  + n n b = −1.050 · ln x − 0.431 0.758 c = 0.671 · ln x − 0.034 0.741
(19) (1 − v m ) + n n b = −0.900 · ln x − 0.440 0.657 c = 0.604 · ln x + 0.003 0.713
(20) n n  + v f b = −0.197 · ln x − 0.356 0.711 c = −0.902 · ln x − 0.406 0.730
(21) (1 − v m ) + v f b = 0.270 · ln x − 0.557 0.770 c = −0.970 · ln x − 0.137 0.717
(22) n + (1 − v m ) b = 0.973 · ln x + 0.142 0.730 c = −0.805 · ln x − 0.529 0.652
(23) n + v f b = 0.264 · ln x − 0.547 0.805 c = −0.805 · ln x − 0.529 0.652
  • a Excision of two devious points belonging to composites based on P33-CO17-Fe50 and P49-CO26-LO25 matrices.
  • b Dependencies depicted in Figure 6.
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Example of b (A, C, E) and c (B, D, F) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for ultimate strain according to ε m,Fmax (A, B), ε m,Fmax · δ (C, D) and δ, (E, F), where ε m,Fmax values are from Table 5 and δ values from Table 1. [Color figure can be viewed at wileyonlinelibrary.com]
There are six possibilities (A m,Fmax , A m,Fmax · δ, δ, ε m,Fmax , ε m,Fmax · δ and σ m,Fmax · δ), how to interpolate the b and c parameters if the observed property is A Fmax . Usually is better to combine the δ with any property. σ m,Fmax seems inappropriate for interpolation without δ against ε m,Fmax , and A m,Fmax . The most appropriate cases are (structural parameters are written generally as p 1 and p 2):
A c , F max = A m , F max + A m , F max ⋅ d + e ⋅ ln A m , F max ⋅ δ ⋅ p 1 + f + g ⋅ ln A m , F max ⋅ δ ⋅ p 2 (36)
except for the situation if the pair of structural parameters p 1 + p 2 is (1-v m ) + n n .
A c , F max = A m , F max + A m , F max ⋅ d + e ⋅ ln σ m , F max ⋅ δ ⋅ p 1 + f + g ⋅ ln σ m , F max ⋅ δ ⋅ p 2 (37)

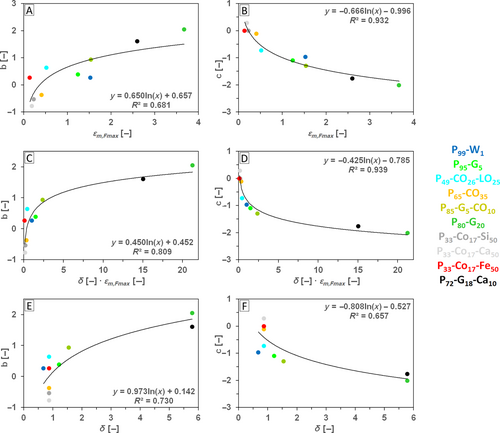
Functions coming from interpolation are in Table 12, which serves as an interpolation overview for interpolations related to A Fmax . The possibilities of interpolation if the pair of structural parameters is n + 1 − v m are in Figures 7 and 8.

TABLE 12. Interpolation possibilities of b and c parameters from Equations (18-23) with general shape z c  = z m  + z m · (b · p 1 + c · p 2) for energy need for ultimate strength achievement according to A m,Fmax , A m,Fmax · δ, δ, ε m,Fmax , ε m,Fmax · δ and σ m,Fmax · δ, where A m,Fmax [kJ m−3] values are from Table 6, ε m,Fmax [–] values are from Table 5, δ values from Table 1 and σ m,Fmax [MPa] values are from Table 4.
Eq. p 1 + p 2 b = f(x); x = A m,Fmax R 2 c = f(x); x = A m,Fmax R 2
(18) n fp  + n n b = −0.750 · ln x + 3.558 0.780 c = 0.720 · ln x − 4.565 0.769
(19) (1 − v m ) + n n b = −0.692 · ln x + 3.397 0.708 c = 0.723 · ln x − 4.662 0.738
(20) n n  + v f b = 0.325 · ln x − 2.681 0.772 c = −0.643 · ln x + 3.052 0.784
(21) (1 − v m ) + v f b = 0.477 · ln x − 4.027 0.782 c = −1.029 · ln x + 6.353 0.840
(22) n + (1 − v m ) b = 0.985 · ln x − 6.117 0.800 c = −0.521 · ln x + 2.168 0.804
(23) n + v f b = 0.468 · ln x − 3.965 0.778 c = −0.525 · ln x + 2.186 0.813
Eq. p 1 + p 2 b = f(x); x = Am,Fmax · δ R 2 c = f(x); x = A m,Fmax · δ R 2
(18) n fp  + n n b = −0.538 · ln x + 2.448 0.904 c = 0.521 · ln x − 3.529 0.907
(19) (1 − v m ) + n n b = −0.480 · ln x + 2.219 0.683 c = 0.505 · ln x − 3.457 0.723
(20) n n  + v f b = 0.238 · ln x − 2.219 0.887 c = −0.457 · ln x + 2.057 0.854
(21) (1 − v m ) + v f b = 0.351 · ln x − 3.351 0.921 c = −0.735 · ln x + 4.750 0.931
(22) n + (1 − v m ) b = 0.719 · ln x − 4.677 0.925 c = −0.374 · ln x + 1.371 0.903
(23) n + v f b = 0.346 · ln x − 3.307 0.920 c = −0.376 · ln x + 1.370 0.903
Eq. p 1 + p 2 b = f(x); x = δ R 2 c = f(x); x = δ R 2
(18) n fp  + n n b = −1.257 · ln x − 0.578 0.804 c = 1.234 · ln x − 0.606 0.830
(19) (1 − v m ) + n n b = −0.992 · ln x − 0.612 0.398 c = 1.064 · ln x − 0.486 0.438
(20) n n  + v f b = 0.570 · ln x − 0.871 0.777 c = −1.045 · ln x − 0.553 0.678
(21) (1 − v m ) + v f b = 0.806 · ln x − 1.300 0.790 c = −1.599 · ln x + 0.434 0.719
(22) n + (1 − v m ) b = 1.622 · ln x − 0.477 0.771 c = −0.823 · ln x − 0.823 0.716
(23) n + v f b = 0.795 · ln x − 1.291 0.796 c = −0.823 · ln x − 0.823 0.716
Eq. p 1 + p 2 b = f(x); x = ε m,Fmax R 2 c = f(x); x = ε m,Fmax R 2
(18) n fp  + n n b = −0.836 · ln x − 1.318 0.659 c = 0.855 · ln x + 0.137 0.738
(19) (1 − v m ) + n n b = −0.627 · ln x − 1.094 0.380 c = 0.687 · ln x + 0.036 0.437
(20) n n  + v f b = 0.385 · ln x − 0.553 0.723 c = −0.667 · ln x − 1.121 0.564
(21) (1 − v m ) + v f b = 0.546 · ln x − 0.873 0.757 c = −0.521 · ln x − 1.249 0.599
(22) n + (1 − v m ) b = 1.058 · ln x + 0.372 0.685 c = −1.092 · ln x − 0.417 0.700
(23) n + v f b = −0.523 · ln x − 1.260 0.596 c = −0.523 · ln x − 1.260 0.596
Eq. p 1 + p 2 b = f(x); x = εm,Fmax · δ R 2 c = f(x); x = ε m,Fmax · δ R 2
(18) n fp  + n n b = −0.572 · ln x − 1.031 0.817 c = 0.575 · ln x − 0.159 0.883
(19) (1 − v m ) + n n b = −0.437 · ln x − 0.906 0.440 c = 0.475 · ln x − 0.170 0.497
(20) n n  + v f b = 0.261 · ln x − 0.679 0.846 c = −0.463 · ln x − 0.903 0.692
(21) (1 − v m ) + v f b = −0.376 · ln x + 1.044 0.889 c = −0.749 · ln x − 0.074 0.817
(22) n + (1 − v m ) b = 0.739 · ln x + 0.039 0.830 c = −0.369 · ln x + 0.745 0.745
(23) n + v f b = −0370. · ln x − 1.038 0.895 c = −0.369 · ln x − 1.096 0.737
Eq. p 1 + p 2 b = f(x); x = σm,Fmax · δ R 2 c = f(x); x = σ m,Fmax · δ R 2
(18) n fp  + n n b = −0.887 · ln x − 0.543 0.765 c = 0.806 · ln x − 0.609 0.677
(19) (1 − v m ) + n n b = −0.887 · ln x − 0.414 0.798 c = 0.900 · ln x − 0.669 0.785
(20) n n  + v f b = 0.362 · ln x − 0.878 0.670 c = −0.786 · ln x − 0.478 0.823
(21) (1 − v m ) + v f b = 0.523 · ln x − 1.402 0.669 c = −1.172 · ln x + 0.726 0.776
(22) n + (1 − v m ) b = 1.137 · ln x − 0.736 0.760 c = −0.630 · ln x − 0.656 0.841
(23) n + v f b = 0.511 · ln x − 1.388 0.660 c = −0.634 · ln x − 0.664 0.845
  • a Dependencies depicted in Figure 7.
  • b Dependencies depicted in Figure 8.
Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Example of b (A, C, E) and c (B, D, F) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for energy need for ultimate strength achievement according to A m,Fmax (A, B), A m,Fmax · δ (C, D) and δ (E, F), where A m,Fmax values are from Table 6 and δ values from Table 1. [Color figure can be viewed at wileyonlinelibrary.com]
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Example of b (A, C, E) and c (B, D, F) parameters interpolations coming from fitting Equation (22) z c  = z m  + z m · (b · n + c · (1 − v m )) derived for energy need for ultimate strength achievement according to ε m,Fmax (A, B), ε m,Fmax · δ (C, D), and σ m,Fmax · δ (E, F), where ε m,Fmax values are from Table 5, δ values from Table 1, and σ m,Fmax values are from Table 4. [Color figure can be viewed at wileyonlinelibrary.com]

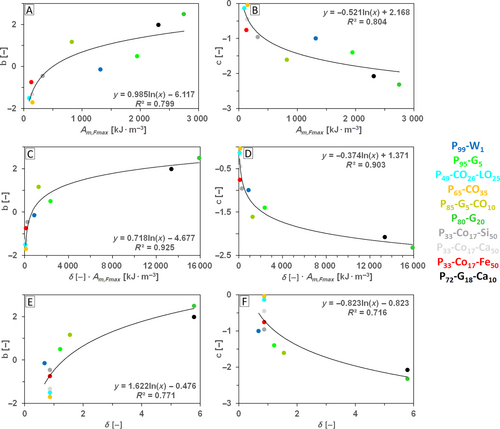
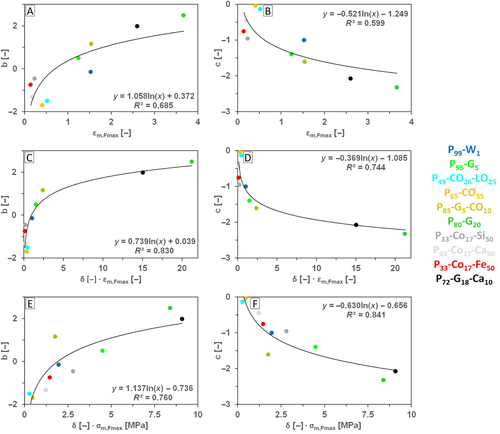
There are many d, e, f, and g parameters in the equations shown in Tables 9–12. What is their function or meaning? The assumption is that parameters d, e, f, and g in the equations should vary according to the pair of filler and matrix in composites. These parameters are the last members in equations without proven meaning and description. On the other hand, the properties and behavior of fillers, their influence on material porosity, and other material properties are the undescribed parts of the composite material description in this work. Therefore, there is an assumption to join parameters d, e, f, and g and fillers properties together, but without accurate description, due to data focusing on different matrices and not focusing on different fillers with their properties and influence on material porosity in this work.

There is a simplification of proposed relationships in case of the material complexity reduction from porous composite to nonporous composite (n; n n  = 0, remaining parameters reduced to v f ) or porous matrix (n fp ; v f  = 0, remaining parameters reduced to n). Equation (17) changes into general Equation (38), and Equations (18-23) changes into Equation (39) for nonporous composite or Equation (40) for porous matrix.
z c = z m + z m ⋅ b ⋅ p (38)
z c = z m + z m ⋅ b ⋅ v f (39)
z mn = z m + z m ⋅ b ⋅ n (40)
where z mn is generally labeled property value valid for porous matrix. Equations (28-37), which contain the results of interpolations, should be simplified too. This approach should be accepted for Equation (39), which is valid (mathematically) for cases of filled composites without porosity. There should also be only two interpolation parameters (labeled d and e or f and g) valid for cases of missing porosity in material because of only one fitting parameter—b. However, the behavior between matrix and filler can vary seriously because of many kinds of potential matrices and fillers. Equation (39) then assumes generally a lot of different possible relationships between filler and matrix, and two remaining interpolation parameters should vary according to filler and its relation to the matrix.

Therefore, there is also an assumption (or idea) of the extra d and e parameter values in the case of a porous matrix without filler if there is an assumption of dependence of d, e, f, and g on filler properties in composites. The potential interpolation is easy because only the b parameter is present in Equation (40), which leads to two interpolation parameters—d and e. Values of these parameters should exist as interpolation results of b parameters of porous matrices if filler absence is as filler type. The reduction of interpolation parameters then should lead to universal interpolation parameters in the case of Equation (40). Parameters d and e should become numbers in that case. However, there are possible influences of different void shapes on material behavior in the case of filler absence. It is indicated in the literature [40, 42, 43]. On the other hand, there is a question about its relevancy from a macroscopic point of view to the properties of material containing voids negligible in comparison with the dimensions of the material body as is suggested in this work. However, only a limited data set was available, but it was trying to find universal d and e parameters for Equation (40). The attempt is later. In contrast with Equation (40), the interpolation joined with nonporous composites (Equation 39) was not tried because they were not available.

It is no fitting possibility for porous matrices as in the case of the porous composites because each matrix has only one porosity value (except the P99-W1 prepared with two porosity values). The process has to be different, and the results should be less accurate. The members of Equation (40) are from various sources. The measured z mn values for porous matrices and fitted z m values for nonporous matrices from the fitting of data belonging to porous composites are in tables including Tables 3–6 according to chosen property. The porosity value has the origin in Equation (6). The member b is the only remaining unknown calculated by known members. Equation (40) can have more versions because this equation can have the source of z m in different Equations (18-23) adapted to the chosen property, so the z m values are various due to the origin of the equation. It leads to several similar variants of Equation (40) b parameters presented for E and σ Fmax . The b interpolations possibilities are in Table 13. The example based on the 1 − v m and n parameters (also Equation (22)) is in Figure 9. The interpolations of ε Fmax and A Fmax were not successful. There are only hints of dependencies. The possible explanation is the absence of fitting and its replacement by calculations. It is necessary to perceive, that each b parameter arose from the fitted z m value of composites and measured values of n and z mn representing the low amount of samples (1 set = 5 identical samples). The assumption is its relevancy is lower when compared with the parameter b obtained by fitting several sets of identical samples (different sets = different porosity and sample properties). Therefore, inaccurate results are in Table 13.

TABLE 13. Interpolation possibilities of b parameters from Equation (40) with general shape z mn  = z m  + z m · b · n for elastic modulus/ultimate strength according to E m and E m · δ/σ m,Fmax , and σ m,Fmax · S m,rel , where E m [MPa] values are from Table 3, σ m,Fmax [MPa] values are from Table 4, δ values from Table 1 and S m,rel from Equation (8).
Elastic modulus
Eq. p 1 + p 2 → p b = f(x); x = E m R 2 b = f(x); x = E m · δ R 2
(18) → (40) n fp  + n n  → n b = −1.882 · ln x + 3.461 0.533 Not found —
(19) → (40) (1 − v m ) + n n  → n b = −11.24 · ln x + 24.14 0.777 b = −7.49 · ln x + 19.66 0.562
(20) → (40) n n  + v f  → n b = −5.68 · ln x − 11.68 0.816 b = −3.302 · ln x + 8.396 0.458
(21) → (40) (1 − v m ) + v f  → n b = 2.861 · ln x − 8.887 0.598 b = 2.566 · ln x − 8.937 0.783
(22) → (40) n + (1 − v m ) → n b = −3.179 · ln x − 9.579 0.586 b = 2.915 · ln x − 9.786 0.792
(23) → (40) n + v f  → n b = 3.348 · ln x − 9.985 0.600 b = 3.040 · ln x − 10.14 0.795
Ultimate Strength
Eq. p 1 + p 2 → p b = f(x); x = σ m,Fmax R 2 b = f(x); x = σ m,Fmax · S m,rel R 2
(18) → (40) n fp  + n n  → n b = −13.56 · ln x + 9.92 0.664 b = −14.69 · ln x + 0.26 0.658
(19) → (40) (1 − v m ) + n n  → n b = −20.92 · ln x + 16.19 0.739 b = −24.95 · ln x − 0.41 0.730
(20) → (40) n n  + v f  → n b = −18.50 · ln x − 13.11 0.727 b = −21.25 · ln x − 0.71 0.724
(21) → (40) (1 − v m ) + v f  → n b = −9.451 · ln x + 7.829 0.701 b = −11.56 · ln x − 0.16 0.749
(22) → (40) n + (1 − v m ) → n b = −20.92 · ln x + 16.19 0.738 b = −23.48 · ln x − 1.11 0.736
(23) → (40) n + v f  → n b = −9.493 · ln x − 7.874 0.706 b = −11.63 · ln x − 0.13 0.756
  • Note: Dependencies labeled by Equation (22) → (40) and parameters n + (1 − v m ) → n are in Figure 9.
  • a Removal of a point belonging to the P65-CO35 matrix due to its devious position, if needed.
  • b Dependencies depicted in Figure 9.
Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Dependencies of b parameters values coming from Equation (40) z mn  = z m  + z m · b · n derived from Equation (22) valid for elastic modulus (A, C) and ultimate strength (B, D) on E m (A), E m · δ (C), σ m,Fmax (B), and σ m,Fmax · S m,rel (D), where E m values are from Table 3, σ m,Fmax values are from Table 4, δ values are from Table 1, and S m,rel values from Equation (8). [Color figure can be viewed at wileyonlinelibrary.com]
Nevertheless, despite this, the obtained results are supposed to be evaluated. The data in Table 13 show different results in the case of E according to the origin of z m . When the z m comes from Equations (18-20), Equation (41) is better for an interpolation of the b parameter from Equation (40). Against this, the z m values from Equations (21-23) lead to Equation (42). The combinations of Equation (42) with Equations (21-23) lead to relatively high R 2 (nearly 0.8) and numerically closed values of d and e parameters (see Table 13). The high R 2 value is important. It would be suitable to increase it. A possible way of getting b parameter values is by fitting several matrices with different (controlled) porosity values (not possible in the case of our matrices)—the same mean as used for composites.
b = d + e ⋅ ln E (41)
b = d + e ⋅ ln E ⋅ δ (42)
There are different versions of Equation (40) in the case of σ Fmax without any significant advantage in the case of one of them against the second.
b = d + e ⋅ ln σ m , F max (43)
b = d + e ⋅ ln σ m , F max ⋅ S m , rel (44)

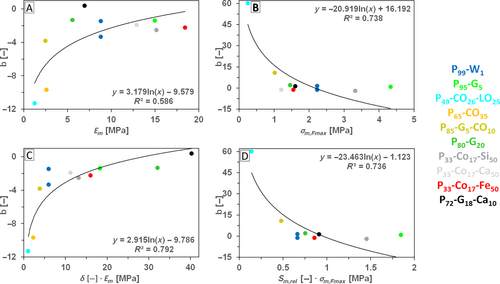
3.4 Discussion With Comparison to Earlier Published Results

This work adds another insight to previous articles [32, 33] presenting Equations (1-3) that are possible to rewrite in one general form as:
z c = z m ⋅ p 1 b ⋅ p 2 c (16)
And it introduces another equation shape ensuring the same phenomenon.
z c = z m + z m ⋅ b ⋅ p 1 + c ⋅ p 2 (17)
where p 1 and p 2 parameters have overturned values to Equation (16) and b and c members are numerically different.
It is impossible to avoid a comparison of Equations (16 and 17) from many perspectives in the discussion part. Although this work also describes relationships between structure/composition and mechanical properties of porous composites which means the same phenomenon as in the previous articles, by a little different means than in previous works, it is not a negation of the previous work [32, 33]. It is another point of view using little various means. Our opinion is that both equation shapes are interesting for further research. In this level of rough results, it is necessary to publish them both to be widely available to researchers. The decision of which shape is better is difficult. For instance, the fitting leads to different z m values (z m values from measurement were not available for comparison). It is impossible to decide now which result of the fitting is more appropriate in certain situations. The following research focused on composites based on nonporous matrices should answer for a direct comparison of fitted and measured z m values. They could be inseparable and have to exist next to each other because their structural parameters are connected in mathematical relationships—see Equation (9). If is this valid, there is some basic idea connecting all equations in this work and those previous [32, 33]—presence of two suitable structural parameters and two describable fitting parameters in the equation. Although Equation (17) has one more member than Equation (16), the mathematical relationships are simpler in Equation (17) due to the absence of exponents and occurring mathematical sign types. The result of using the new structural parameters is the shape of Equation (17), which has to be linear if it is supposed to work correctly with the chosen structural parameters. However, they include more rich functions b = f(c) in each fitted equation (see Table 7, not found in Equation (16)). Fitting leading to Equation (17) is not done only according to R 2 but also by the z m fixation by the same value for slope and displacement. The interpolations are similar, with some variability, but the most common case is:
b = d + e ⋅ ln z m ⋅ δ ; c = f + g ⋅ ln z m ⋅ δ (45)

Equation (17) has three versions based on three structural parameters pairs created by three parameters (n, v f , 1 − v m instead of n p , 1 − v f , and v m from Equation (16)) and leading to the nearly same z m values if they are compared (see Tables 3–6). The exact connection between the results from Equations (16 and 17) does not exist. The exception is only the Equation (9) dedicated to structural parameters. Further research should solve this problem after using nonporous matrices with the following direct comparison to measured and fitted values. There are also simple dependencies between b and c across different equations differing by structural parameters (n, v f , 1 − v m as example) in both relationships represented by Equations (17 and 16) (see Table 8 for Equation (17)). The possibility of simplified equations for nonporous composite (theoretically) and porous matrix (tested) is also valid for both approaches.

The primary data included materials with different matrices, various porosity rates (up to 50 vol% without the possibility of influence of its value during the preparation in a more significant way), and only one type of filler (but including various filler contents). The filler behavior then cannot be accented in the shapes of relationships now. It could be included in the interpolation parameters d, e, f, and g with unclear behavior after research of composites based on different matrices but no fillers. Further research should focus on filler size distributions, surface values, surface properties, and their interaction with matrices. The surface properties of material components related to their adhesion should replace the δ value used as a simplification.

This work does not differ in the porosity type (open or closed pores) by visible means. There is an expectation that the porosity type (and its content in material) is a result of several factors such as matrix type, filler type, their rates, and ambient conditions affecting the porosity of the sample during its preparation—the pressing, for example. All these factors are directly or indirectly present in equation members, respectively, and their influence on them is expected (filler properties). There is also the question of the influence of void shapes and distribution to d and e parameters in simplified equations valid for porous matrices if the work focuses on the macroscopic point of view concerning the properties of components. Parameters d and e could be universal numbers for each one-component porous material, but it is necessary to prove it first. This work includes some effort to solve it. The limited data lead to only indication of results (low R 2), and this work should be repeated in another way in the future (more matrices with controlled porosity values for fitting, different shapes of voids if possible). Nevertheless, it is the first important step indicating future possibilities.

The proposed relationships for composites can process the data from materials on both sides of the percolation threshold in porosity/filler concentrations. It suggests an idea of utilization of similar equations in many different cases of not only the mechanical properties of materials.

The adjusted data processing approach could lead after discovering all relevant influences to relationships containing parameters adjustable according to types and rates of materials components. This approach could compose the composite behavior from the values of members in equations determined by the behavior of present components and their rates influenced by porosity if it would be present.

The base of our approach is relationships containing members determined accurately or approximately by their positions in equations and mathematical relations. First, materials with different compositions based on different matrices, fillers, and porosity can be prepared and tested. The work method is based on fitting measurement results to get an equation followed by equation members interpolation according to some properties and relations of components to find their mathematical behavior joined or comparable with the observed properties of components or the whole material.

It differs from most published works dedicated to physical models, where there is an accurate physical assumption at the beginning. This physical assumption is then compared with the behavior of existing material with some extent of accordance. The reason is simplification at the beginning—in material structure. In the model, it is hard to describe random structures containing randomly shaped particles and then randomly shaped pores. The expectations include granular particles [30], short fibers with cylindrical shapes [28], nanotubes or nanoparticles [23, 24] or unidirectionally oriented nanofibers [27] for example. Forms of voids can be limited to spherical [25]. The models are often limited to some properties. Examples include the elastic region of loading [21, 26-28] or the study of nonlinear stress [22-24, 29, 30]. The models can use different mathematical methods [21, 27-29].

The advantage of models is their awareness of physical rules, but there is often a problem with materials embodying random structures. Our proposed approach can work with randomly structured material due to its macroscopic point of view, and then it can describe also some stochastic properties, but not as well as elastic modulus. However, it does not work directly with an accurate physical description of the material on its microscopic level. Therefore, its understanding of phenomena occurring at a microscopic level is limited. It only connects the measured data with known properties of material components and structural parameters such as filler volume fraction, etc. These two approaches do not have to stand against each other. If our system were more complex (including also different filler types and maybe void types if it they are relevant), both approaches could meet in cases of material with a structure corresponding to limits of models such as spherical particles and voids, cylindrical particles, and so forth. This potential meeting or connection could contribute to understanding materials with different types of composition and structure complexity.

Our system of fitting and interpolating in presented forms comes from limited data set and needs continuation to solve a lot of question coming from proposed equations as filler and voids influence on material behavior.

4 Conclusions

This work introduces new forms of description for relationships between structure/properties and chosen mechanical properties from tensile testing of porous materials (mainly filled composites, not reinforced). It uses the mean when the measurement is the beginning, the data fitting follows, and further interpolation of obtained parameters is the finish. The proposed relationships used structural parameters leading to a new shape of fitting functions (spatial linear with displacement). The fitting is newly based not only on the value of the R 2 coefficient but also on the similarity of slope and displacement values (they should be ideally the same) in the linear fitting function. The following interpolation gives real meaning to obtained parameters.

The proposed function shape is z c  = z m  + z m · (b · p 1 + c · p 2), where z c /z m is generally labeled mechanical property value for composite/nonporous matrix, p 1 /p 2 are suitable structural parameters, and b/c are fitting parameters subjected to interpolations by logarithmic function containing values of properties typical for matrices. The interpolations were done by as many means as possible to obtain many interpolation results. It serves as an indication of the potential research directions. The logarithmic functions interpolating the b and c parameters contain d, e, f, and g members without clear description. On the other hand, the work is not focused on different matrices and porosity types. Therefore, these interpolation members could be related to these material components and their behavior. The members p 1 and p 2 represent structural parameters including v f (filer volume fraction), 1 − v m (volume fraction of filler and porosity together), n (porosity), n fp (filler volume fraction, if porosity neglect), and n n (interspace porosity) used in pairs. Combinations of the trinity of parameters—1 − v m , v f , and n make the connection of proposed equations that include them. There is a connection of b and c parameters across equations and the retaining of slope and displacement values across different equations (if the property is the same). It is not valid for pairs p 1 and p 2 created by another combination of structural parameters. Another interesting result is the linear dependence of c on b in each proposed equation unconnected with the choice of structural parameters.

The proposed equations enable mathematical simplification if the corresponding material is simpler (without pores or filler) to only one structural parameter, one fitting parameter (b), and two interpolation parameters (d, e). The version valid for porous matrices was proven and the results were interesting but not sufficiently suitable due to the low amount of available data. The results are important because they indicate potential future research directions. The nonporous composites were not available and practically studied except for mathematically deriving their equation.

This work introduces new means of data processing that are non-exclusive to those earlier published and mentioned in this work as references or for comparisons. The results are rough, but they are shown in numerical forms (equations, values in tables) to enable easier looking for utilizable ways in further research. The most significant output of this work is the general shape of equations and mean of work (fitting, interpolation). The general output is more significant than individual results of fitting and interpolation, which are only its support.

Section 3 discusses the potential relationship of our work to physical models as another approach for investigating composite materials. Currently, there is no connection, but this could change in the future.

Author Contributions

Miroslav Černý: conceptualization (lead), data curation (equal), formal analysis (lead), investigation (lead), methodology (equal), writing – original draft (lead). Přemysl Menčík: conceptualization (supporting), data curation (equal), funding acquisition (lead), investigation (supporting), methodology (equal), writing – review and editing (lead).

Acknowledgments

This work was supported by the Brno University of Technology [Specific University Research Grant FCH-S-23-8208]. Open access publishing facilitated by Vysoke uceni technicke v Brne, as part of the Wiley - CzechELib agreement.

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Data Availability Statement

    The data that support the findings of this study are available from the corresponding author upon reasonable request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.