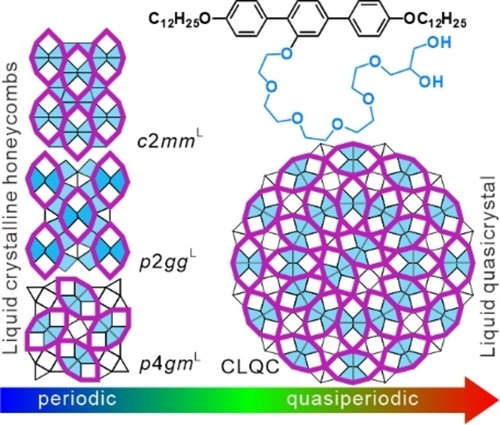
Understanding the Role of Trapezoids in Honeycomb Self-Assembly—Pathways between a Columnar Liquid Quasicrystal and its Liquid-Crystalline Approximants
Graphical Abstract
T-shaped polyphiles self-assemble into a liquid quasicrystal and a series of liquid-crystalline periodic approximants, all representing polygonal honeycombs formed by the stacking of p-terphenyls. Featuring giant octagonal motifs containing non-regular trapezoidal or pentagonal with regular triangular and square tiles, the phases assume a transition of motif orientation, triggered by the changing conformation and entropy of the alkyl end chains.
Abstract
Quasiperiodic patterns and crystals—having long range order without translational symmetry—have fascinated researchers since their discovery. In this study, we report on new p-terphenyl-based T-shaped facial polyphiles with two alkyl end chains and a glycerol-based hydrogen-bonded side group that self-assemble into an aperiodic columnar liquid quasicrystal with 12-fold symmetry and its periodic liquid-crystalline approximants with complex superstructures. All represent honeycombs formed by the self-assembly of the p-terphenyls, dividing space into prismatic cells with polygonal cross-sections. In the perspective of tiling patterns, the presence of unique trapezoidal tiles, consisting of three rigid sides formed by the p-terphenyls and one shorter, incommensurate, and adjustable side by the alkyl end chains, plays a crucial role for these phases. A delicate temperature-dependent balance between conformational, entropic and space-filling effects determines the role of the alkyl chains, either as network nodes or trapezoid walls, thus resulting in the order-disorder transitions associated with emergence of quasiperiodicity. In-depth analysis suggests a change from a quasiperiodic tiling involving trapezoids to a modified one with a contribution of trapezoid pair fusion. This work paves the way for understanding quasiperiodicity emergence and develops fundamental concepts for its generation by chemical design of non-spherical molecules, aggregates, and frameworks based on dynamic reticular chemistry.
Introduction
Complexity has become a crucial concept in scientific research, allowing us to explore a broad range of phenomena in nature.1 Chemistry develops complexity by self-assembly and self-organization, which are driven by the interplay of electromagnetic interaction forces, governed by the shape and chemical structure of the molecules, and the effects of entropy. Liquid crystals (LCs) are condensed matter systems that combine fluidity with long range order, offering a fascinating example of a highly dynamic mode of molecular self-assembly2 with numerous applications.3 The molecular dynamics within LC systems enables the selection of competing self-assembled structures, leading to the emergence of structural complexity and new properties in molecular4 and macromolecular5 systems.
In previous work we have shown that the competition between shape-determined packing and nano-segregated packing of so-called polyphilic molecules (i.e. amphiphiles combining more than two incompatible units) involving a rod-like unit can lead to new 2D and 3D LC phases with unprecedented complexity.4b, 6 A noteworthy example is the spontaneous emergence of honeycombs with Archimedean and Laves tilings in LC phases of T-shaped polyphiles (Scheme 1c).7 There are two types, bolapolyphiles having polar groups at both ends of a linear polyaromatic core unit and bearing one or more lipophilic side chains (Scheme 1a),6, 8 and facial polyphiles with inverted structure, i.e. having a polar side chain and lipophilic end chains (Scheme 1b).9 In the polygonal honeycombs of these polyphiles the side chains form columns which are framed by walls involving the p-terphenyls organized perpendicular to these columns and the end chains linking them together at the edges (Scheme 1c).
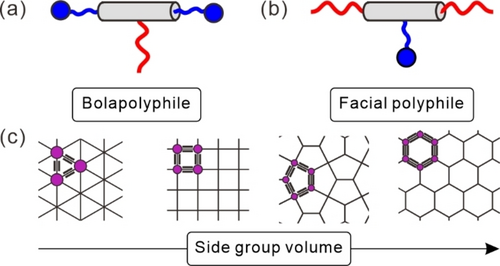
(a, b) Schematic representations of the basic structures of the T-shaped polyphiles and (c) examples of polygonal honeycombs (cuts perpendicular to the prismatic cell long axis), representing tilings with congruent tiles;7a side-by-side pairs of the rod-like units (black thick lines) form the walls of the polygonal cells, while the end groups form the nodes (purple circles) and the side groups fill the interior.
Recently, it was shown that these tilings are not restricted to periodic structures,6f but also provide a new source of soft quasicrystals (QCs),10 in which orientational order is preserved while translational periodicity is absent. Unlike QCs in alloys or spherical aggregates,11 T-shaped polyphiles form columnar liquid quasicrystals (CLQCs), i.e., 3D structures with 2D-quasiperiodicity and having a polygonal honeycomb structure composed of triangular, square, and trapezoidal prismatic cells. More interestingly, such CLQC represents the first case of a self-assembled uniform long range dodecagonal soft matter tiling with quasiperiodicity, which was never observed before11, 12 and even thought to be impossible for tiling without the trapezoidal tiles.13 This inspired us to explore the role of this tile during self-assembly. However, in these previously reported ionic compounds Am/m′ (Scheme 2) the strong incompatibility between the ionic side chain and the less polar terphenyls and alkyl end chains favor the development of a hexagonal channeled lamellar phase (ChLhex, see Scheme 2), where the terphenyls are arranged parallel to the columns of the side chains, thus removing the honeycomb structure, as for example, observed for A12/12.9b, 14 Only compound A16/6 with two very different chain lengths at both ends suppresses this phase—at least partly—and in this case the CLQC can be observed. This competition restricts the possible structural modifications and becomes an obstacle for further research on these CLQCs.
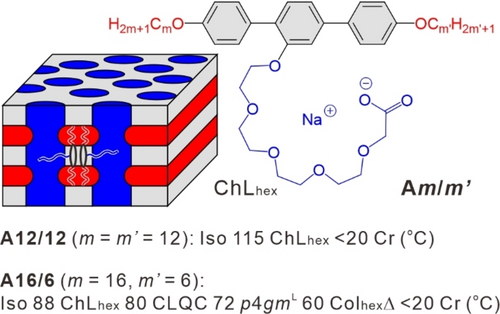
Structures of the previously reported facial amphiphiles Am/m′10, 14 with their phase transitions, as observed on cooling from the isotropic liquid (Iso). abbreviations: Cr=crystalline state; CLQC=columnar liquid quasicrystal with 12-fold symmetry; p4gmL=honeycomb with a square superlattice composed of square, triangular, and trapezoidal cells; ColhexΔ=honeycomb LC with hexagonal lattice formed by triangular cells.
In this work, we focus on the self-assembly of three new T-shaped facial polyphiles, denoted as 12/4, 12/5 and 12/6 (see Figure 1a). By utilizing the less polar hydrogen bonding of the glycerol unit as cohesive force, a weaker segregation of the lateral chains from the aromatic rods is achieved which removes the competing ChLhex phase and allows a more comprehensive exploration of CLQCs. However, there is no specific effect of the (local) hydrogen bonding directionality on the mode of self-assembly as discussed in Section S4.7. Nevertheless, for these compounds a remarkable series of five complex honeycomb phases including a CLQC will be reported. In-depth analysis of the small-angle X-ray scattering (SAXS) pattern reveals that pairs of trapezoids can partly or fully fuse to pentagons which provides a new approximant structure and modifies the structure of the new CLQC compared to the reported case.10
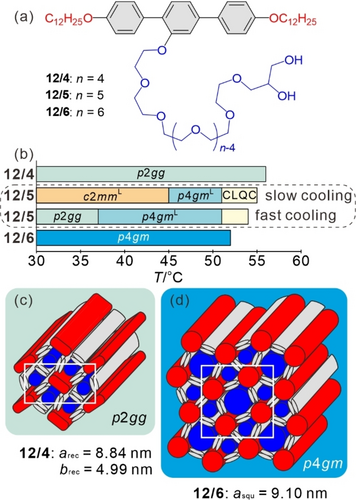
a) Molecular structures and b) phase transitions of compounds 12/4–12/6 as observed on cooling with a rate of 10 K ⋅ min−1, slow cooling was performed at 1 K ⋅ min−1; abbreviations: p2gg=rectangular lattice formed by trapezoidal cells; c2mmL=rectangular superlattice with square and trapezoidal tiles; p4gm=square lattice with square and triangular tiles in a ratio of 1 : 2; for the other abbreviations, see Scheme 2; the Iso state is on the right side of the bars; for numerical values of the phase transitions, see Figures 2a,b and S13. c,d) Models of the p2gg and p4gm columnar phases of compounds 12/4 and 12/6, respectively.
Results and Discussion
The synthesis of these compounds 12/4–12/6 (Figure 1a) is shown in Scheme 3 and the detailed procedures and analytical data are given in Section S1 of the Supporting Information. All compounds were prepared from racemic 1,2-O-isopropylidene glycerol and thus represent racemic mixtures, eliminating any influence of permanent molecular chirality on self-assembly.
Synthesis of compounds 12/n (n=4–6).
Compounds involving EO units are known to easily absorb water. For this reason, before investigation, the samples of compounds 12/4–12/6 were carefully dried by annealing an open sample at 140 °C for 2 min to remove all absorbed water traces, followed by immediate sealing, for more details, see Section S2.
While compounds 12/4 and 12/6 each form only one single LC honeycomb phase, either composed of trapezoidal cells in the p2gg phase9d of 12/4 with arec=8.84 nm and brec=4.99 nm, or a mixture of square and triangular cells with a ratio of 1 : 2 in the p4gm phase9c of 12/6 (asqu=9.10 nm, see Figures 1c,d, S10, S13, S20 and Tables S8 and S9), a series of in total 5 different honeycomb phases with complex supertiling patterns including a CLQC phase were found for the intermediate homologue 12/5 (see Figures 1, 2 and Table 1), revealing pathways between periodic and quasiperiodic tiling patterns.
Comp. |
Phase |
Lattice parameters /nm |
Unit cell volume /nm3 |
ncell |
nside |
nwall |
|---|---|---|---|---|---|---|
12/4 |
p2gg |
arec=8.84 brec=4.99 (52 °C) |
19.9 |
13.2 |
6 |
2.2 |
12/5 |
p4gmL |
asqu = 16.97 (51 °C) |
129.6 |
85.9 |
36 |
2.5[b] |
12/5 |
p2ggL |
arec=17.32 brec=18.85 (45 °C) |
146.9 |
93.1 |
34 |
2.7 |
12/5 |
c2mmL |
arec=15.96 brec=8.23 (35 °C) |
59.1 |
37.5 |
16 |
2.3 |
12/5 |
p2gg |
arec=9.17 brec=5.14 (32 °C) |
21.2 |
13.4 |
6 |
2.2 |
12/6 |
p4gm |
asqu=9.10 (43 °C) |
37.3 |
23.6 |
10 |
2.4 |
- [a] ncell=number of molecules per imaginary unit cell with a height of 0.45 nm, nside=number of polygon sides (honeycomb walls) per unit cell formed by the p-terphenyl cores, and nwall=average number of molecules in the lateral cross section of the honeycomb walls; see Section S4.1 for more details. [b] Only one single molecule is assumed for the inter-trapezoidal wall.
An investigation of a dry sample of 12/5, conducted by polarizing optical microscopy (POM) (see Section S3.1 and Figures S7, S8) and differential scanning calorimetry (DSC) indicates a series of birefringent mesophases (see Figures 1b, 2a,b and S12). All the mesophases exhibit sharp peaks in the SAXS (Figure 2c), and only one diffuse scattering in the wide-angle X-ray scattering (WAXS) (Figure S14), suggesting mesophases with long-range order but without defined positions of individual molecules. Furthermore, all mesophases were found to be easily sheared, confirming their fluid nature.

Investigation of dry compound 12/5. a,b) DSC traces as measured a) upon slow cooling from Iso followed by slow heating (1 K ⋅ min−1) and b) upon fast cooling/heating (10 K ⋅ min−1; peak temperatures, followed by transition enthalpies [ΔH/kJ ⋅ mol−1]); transitions without enthalpy were taken from SAXS investigations. Cooling was conducted to ≈30 °C to avoid crystallization; DSC traces over wider temperature ranges, also including crystalline phases and at different rates, are shown in Figure S12; the melting point of the highest melting crystalline modification is 43 °C [ΔH=50.7 kJ ⋅ mol−1], abbreviations: p2ggL=rectangular superlattice with non-regular pentagonal, square, trapezoidal and triangular tiles; for the other abbreviations, see Figure 1 and Scheme 2; for optical textures, see Figures S7 and S8. c) SAXS cooling scan; due to the holding times during exposures, effectively an intermediate cooling rate was used, which allows the detection of all LC phases observable on cooling, see Section S3.4 for more details.
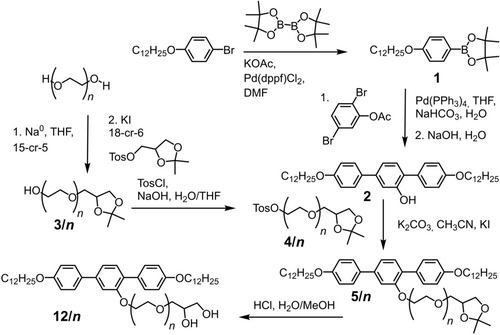
Upon cooling compound 12/5 from the isotropic liquid state, a spherulitic texture was observed between crossed polarizers, indicating the transition to a columnar mesophase at the first phase transition at 54–55 °C (Figure 3a). Dark areas in this texture indicate a uniaxial columnar phase with an alignment of the columns perpendicular to the substrate surfaces, while in the birefringent spherulites they are aligned parallel to the surfaces. Investigation with an additional λ-plate shows a blue shift parallel to the indicatrix slow axis (blue arrow) and confirms that the main (slow) optical axis is perpendicular to the column direction (Figure 3b). This is typically observed for honeycomb structures, where the major π-conjugation pathway (slow axis) is along the rod-like cores forming the honeycomb walls.
CLQC phase of compound 12/5 at 55 °C upon cooling: a) the optical texture between crossed polarizers (arrows show the polarizer/analyzer directions) and b) with additional λ-plate (blue/yellow arrows) indicating the direction of the slow/fast axis, respectively; c) SAXS diffractogram and d) GISAXS pattern. The horizontal line represents the cut-off from the sample tilt angle. q1-q4 represent the reciprocal unit vectors. Note that the (2000) peak is only observed in GISAXS. For more details, see Table S1.
The SAXS pattern displays a q2 ratio of the first four peaks of (Figure 3c), suggesting a reciprocal lattice with four basis vectors and 12-fold symmetry, i.e. with an angle of 30° between neighboring vectors. To further confirm this hypothesis, grazing-incidence small-angle X-ray scattering (GISAXS) was applied to the sample film prepared by shearing on a silicon wafer as shown in Figure 3d. The 12-fold symmetry was clearly observed, fitting well with the experimental signals of the recently reported CLQC of A16/6.10
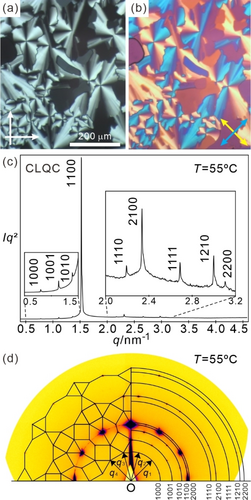
All relevant reciprocal vectors of the CLQC can be regarded as integer combinations of the 2D base vectors of an even larger imaginary extra-large p4gmXL lattice with doubled lattice parameters (Figure S15a, Table S2).15 As explained in ref. [10] and Section S4.6, this p4gmXL lattice was used as imaginary periodic approximant of the CLQC for the calculation of the electron density (ED) map. A patch of the resulting ED map is shown in Figure 4a, where a dodecagonal supertile composed of square, triangular, and trapezoidal tiles can be recognized. Inflation of this dodecagonal supertile according to the inflation rule provides the QC tiling shown in Figure 4b and its further inflations up to the 3rd generation are shown in Figures 4c, S24 and S25. The patch of the ED map in Figure 4a shows a medium ED (green) network formed by the end-to-end connected p-terphenyls, with the alkyl end chains forming low ED nodes (yellow/red), acting as junctions fusing them to a honeycomb. Some of the alkyl chain domains assume a pronounced elliptical cross-sectional shape (green/yellow) and thus act simultaneously as nodes as well as short honeycomb walls of the trapezoidal cells. These walls, formed by alkyl chains, are shared by two trapezoids and these pairs organize side-by-side forming local clusters of four trapezoids which then combine with two squares to give an octagonal supertile (red in Figure 4b) as a basic motif of the CLQC and all the complex LC phases. In the CLQC two of these octagons, together with a square and four additional triangles form a larger dodecagonal supertile which can be further inflated. The polar side chains fill the high ED (blue/purple) polygonal cell, and there is only dodecagonal quasiperiodic order in two dimensions, i.e. in the a/b plane of the 2D network, but no order along the c-direction (honeycomb's long axes). The 2D tiling pattern can be considered as being composed of the overlapping dodecagonal supertiles, or alternatively, as a non-overlapping tiling by the smaller octagonal motifs (shown in red in Figure 4a,b) while additional triangular and square cells fill the space between them.
a) Reconstructed ED map of a patch of a hypothetical approximant of the CLQC phase with an extra-large p4gm lattice (p4gmXL with asqu=32.53 nm). High ED is shown in purple and low ED is in red. The black thick lines represent the aromatic cores while the red line indicates an octagonal motif; b) CLQC tiling inflated once according to the inflation rule;10 the octagonal motifs are highlighted by red color; c) 3rd generation of inflation, see Section S4.2 for details.
Upon cooling, this CLQC phase undergoes a transition to a columnar phase with a periodic p4gm lattice around 51 °C. The SAXS diffractogram (Figure 5a) shows that the lattice parameter of this square phase is 16.97 nm, indicating a superlattice (p4gmL); the GISAXS pattern supports the indexation further (Figure 5b). Figure 5c shows the reconstructed ED map of the p4gmL phase, while Figure 4a displays a patch of the CLQC phase. Both ED maps reveal honeycomb networks composed of squares, triangles, and trapezoids involving high ED areas (blue/purple). Approximately 86 molecules are present in each p4gmL unit cell (ncell), which has a height of h=0.45 nm (see Table 1) and is composed of eight triangles, six squares, and eight trapezoids, with a side-by-side molecular packing mode of the p-terphenyls in the walls forming the periodic honeycomb (Figure 5c). This p4gmL phase is considered as a periodic approximant of the CLQC phase, with a periodic 90° twisted packing of the octagonal tiling motifs (red tiles in Figure 5d). The transition from p4gmL to the CLQC is associated with a small transition enthalpy of ≈0.1 kJ ⋅ mol−1, but it cannot be identified by POM, because both phases are uniaxial and exhibit the same spherulitic texture (Figures S7a,b, S8a–c). We note that the coherence lengths of both, the CLQC and the p4gmL phase, exceed 500 nm, indicating a long range quasiperiodic or periodic order, respectively.
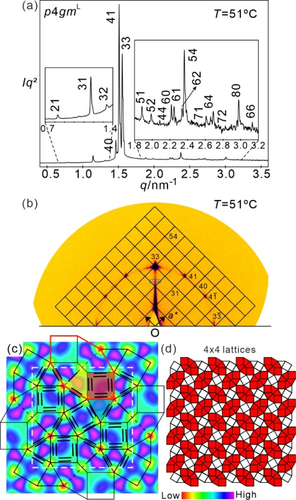
a) SAXS diffractogram, b) GISAXS pattern, and c) reconstructed ED map of the p4gmL phase of compound 12/5 at 51 °C upon cooling. The main orientation of GISAXS is indexed, whereas the others are only weak. The two weak signals in the blue ellipse are different orientations of the (31) peak; for more details, see Table S3; d) shows a tiling with 16 lattices indicating that these octagonal motifs are perpendicular with each other.
Upon slow cooling (Figure 2a), a transition from the square p4gmL phase to a rectangular c2 mm lattice occurs at approximately 45 °C, resulting in a mosaic texture (Figure S7c,d,g), indicating a reduced flexibility of the honeycomb. All mosaics are birefringent at distinct orientations with respect to the crossed polarizers, being a first hint on phase biaxiality. The lattice parameters of this new honeycomb phase are arec=15.96 nm and brec=8.23 nm at 35 °C (Figure 6a,b), indicating a c2mmL superlattice. This phase contains ≈37 molecules in each rectangular unit cell (h=0.45 nm, see Table 1), and all walls are formed by the packing of side-by-side pairs of the p-terphenyl cores as in CLQC and p4gmL. Once formed, the c2mmL phase remains stable down to crystallization (Figures 2a, S7 h,i and S12f). The GISAXS pattern of the c2mmL phase fits perfectly with the SAXS indexation when decomposed into different orientations (Figure S16). The reconstructed ED map of the c2mmL phase (Figure 6c) consists of two squares and eight trapezoids, with the triangular cells removed. Each square is surrounded by four trapezoids, forming the same octagonal motif (encircled by red lines) as observed in the CLQC and p4gmL phases (see Figures 4, 5). However, in the c2mmL phase, the overlapping octagons are aligned parallel (Figure 6d), instead of a 90° twist in the CLQC and p4gmL phase (Figures 4b and 5d). To further validate this complex structure, a geometric model based on the tiling was created. Fourier transform was applied to simulate the scattering intensities and molecular dynamic (MD) simulations were also conducted (see Section S4.3 and Figure S17).
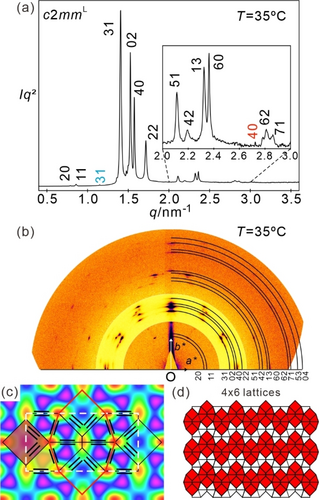
a) SAXS diffractogram, b) GISAXS pattern, and c) reconstructed ED map of c2mmL phase of compound 12/5 at 35 °C upon cooling. The very weak blue peak (31) is from the p4gmL phase and red peak (40) is from the p2gg phase coexisting with c2mmL due to the applied cooling rate. For more details, see Table S4. d) shows 24 lattices indicating that the highlighted octagonal motifs are parallel to each other.
In the heating scan, the c2mmL phase does not directly return to the p4gmL superlattice, but instead, an intermediate phase with a rectangular p2gg superlattice (p2ggL) with lattice parameters arec=17.32 nm, brec=18.85 nm is formed between 45 and 53 °C (Figure 7a). The ED map of the p2ggL phase reveals a complex tiling where the local clusters of four trapezoids are fused to two non-regular pentagons, grouped into dimers with the shared sides being formed by alkyl chains (Figure 7b,c). Similar to the other superlattice phases, the p2ggL phase is composed of side-by-side pairs of p-terphenyls, with slight inward shift of the molecules in the square cells, causing square shrinkage and triangle/trapezoid expansion (Section S4.4). In this new lattice structure, the octagonal supertile motifs (now formed by two pentagons and two squares) are still present and aligned in a parallel fashion, similar to the c2mmL lattice. However, this time they are slightly deformed and separated by additional tiles, including additional pairs of trapezoids and triangular cells (Figure 7b,c) that were not present in the previous lattice structure. This p2ggL phase does not include any regular tile, which results in the p2gg plane group with reduced symmetry and compensates for the increased cell volume caused by the emergent pentagons. In addition, the larger nwall (Table 1) compensates a bit of the cell-volume expansion. We note that this tessellation involves two different types of cells formed by a combination of aromatic (p-terphenyl) and aliphatic (alkyl chain) walls, the previously known trapezoids9d and the new pentagons (fused trapezoid twins, see Figure 7b). Interestingly, the aromatic and aliphatic walls alternate along a larger hexagonal grid (thin dot-dash line in Figure 7b) with smeared-out medium ED (green, yellowish green; see also Figure S15b). This averaging of ED can be explained by some partial mixing of the aromatic cores and alkyl chains, as described previously in another case for hexagonal honeycombs.9b Such mixing introduces some entropy advantage to the p2ggL phase.
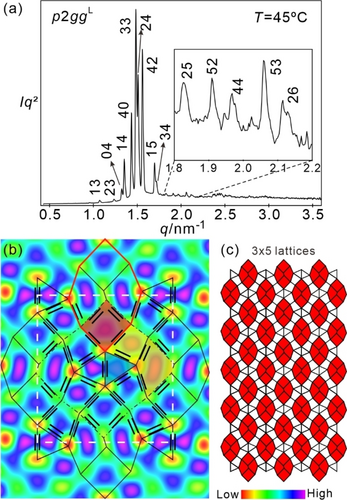
a) SAXS diffractogram of the p2ggL phase of compound 12/5 at 45 °C upon second heating; b) the reconstructed ED map (see also Figure S15b), molecular packing and tiling of the p2ggL phase. The tiling is composed of non-regular trapezoids, squares, triangles, and pentagons; c) a collection of 15 lattices. The highlighted octagonal motifs are parallel with each other and separated by deformed trapezoids and triangular tiles. For more details, see Table S5.
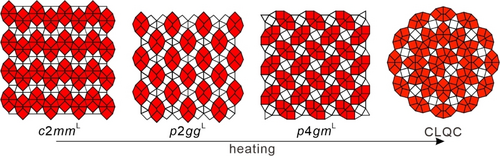
At the lattice transitions to p4gmL on further heating at 53 °C (Figure 2a), the number of triangles doubles and the pentagons split again into two trapezoids. The partial core-chain mixing is also reduced, thus removing some entropy advantage and contributing to a relatively high p2ggL→p4gmL transition temperature and a much narrower temperature range of the p4gmL phase on heating. Thus, the distorted honeycomb network is an intermediate structure at the c2mmL→p4gmL transition and is associated with the change in orientation of the octagonal motifs from a parallel mode in c2mmL to a perpendicular mode in p4gmL (see Figure 8).
Reorientation of the octagonal motifs upon phase transition between the approximants and the CLQC.
Although the c2mmL phase is a thermodynamically stable phase compared to the p4gmL phase below 45 °C, its formation is kinetically hindered on cooling, especially at low temperature. As a result, the emergence of the c2mmL phase is suppressed by rapidly cooling the p4gmL phase at a rate of ≥10 K ⋅ min−1. Instead, a transition to another columnar phase with p2gg lattice occurs at 37 °C (Figures 2b and S8) from the supercooled p4gmL phase. The lattice parameters of this phase at 32 °C are arec=9.17 nm and brec=5.14 nm, similar to the trapezoidal honeycomb of 12/4 (Figures 1c, S18 and S19a). Thus, for compound 12/5 the CLQC phase with dodecagonal symmetry is accompanied by a close approximant (p4gmL) and two other competing LC supertilings (p2ggL, c2mmL) as well as a monohedral trapezoidal honeycomb (p2gg) at lower temperature.
In the contact region between the p2gg phase of 12/4 and the p4gm phase of 12/6, a ribbon with the typical mosaic texture of the c2mmL/p2ggL phases and a second one with the spherulitic texture of the p4gmL/CLQC phases separate these two simple phases (Figure S11). So, all complex mesophases, including the CLQC develop at the transition between p2gg and p4gm by fine-tuning the side chain volume (see Figure 9a–g). As well, all complex phases are removed for a water swollen sample 12/5×3H2O, leaving only p4gm and p2gg (for details, see Figures S9, S19b, S23 and Section S3.3), indicating the significance of side chain volume for the rational design of the CLQC and its approximants (for the effect of water on the mesophases of compounds 12/4 and 12/6, see Section S4.8). Though these volume effects determine CLQC formation in the first place, also geometric restrictions of the tiling patterns are important.
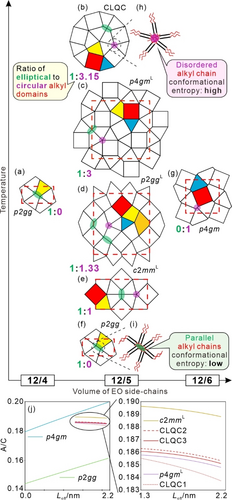
a-g) Tilings observed for compounds 12/4–12/6 depending on the temperature and volume of the EO side chains; h, i) Schemes of a circular (purple) and an elliptical (green) alkyl chain domain and j) development of the A/C ratio depending on the effective side length (Leff, depends on the chain stretching), mesophase type, and inflation of the CLQC. For more details, see Section S4.4.
Tiles can be characterized by the number of edges and area-to-circumference (A/C) ratios with normalized tile edges. Figure 9a-g illustrates the different tiling patterns observed experimentally for compounds 12/4–12/6. Commonly observed triangle and square tiles have A/C values of 0.14 and 0.25, respectively. However, the large difference (≈73 %) between them generates varying space filling and packing densities in neighboring tiles, resulting in steric frustration that needs to be minimized. Square shrinkage and triangle expansion by shifting the p-terphenyls towards the larger cells can partly solve this steric frustration force in the CLQC and its approximants by adjusting the cell volume to side chain volume and by minimizing the side chain stretching required to fill the centers of the cells (see Section S4.4). Another unique aspect of facial amphiphiles is that their alkyl end chains can easily assume different conformations. At higher temperature, conformationally disordered and folded chains dominate and support columns with circular cross section, which creates high conformational entropy. At lower temperature, a larger contribution of linear all-trans conformers16 supports parallel chain alignment and elliptic deformations of these hydrocarbon columns, leading to the development of non-regular polygons with different side lengths, such as trapezoids and non-regular pentagons. The trapezoidal cells have one honeycomb wall made up of alkyl chains (Figure 9f,i), which increases the available space in the cells without contributing to their space filling. As a result, trapezoidal cells provide an efficient way to escape from steric frustration due to overcrowding in triangular or to insufficient space filling in square cells. This also contributes to the stabilization of the CLQC as well as its approximants.
In all honeycomb phases, the lattice parameters increase upon cooling, as shown for the p4gm and p4gmL phases in Figure S21. This lattice expansion upon cooling confirms the postulated stiffening of the terminal alkyl chains at lower temperature, as an increasing elliptical deformation of the alkyl chain columns expands the space available inside the polygons.
This chain stiffening effect also provides a growing number of trapezoidal cells with lowering temperature. The parallel chain alignment (Figure 9i) in the elliptical columns leads to a denser packing of the chains, giving rise to an enthalpic gain, but also to an entropic penalty (reduced conformational entropy of the alkyl chains) if compared with the more circular columns involving more disordered and folded alkyl chains (Figure 9h). As the entropy term TΔS rises with temperature, the formation of these elliptical columns is supported at lower temperature and disfavored at higher temperatures, in agreement with the experimental observed phase sequence p2gg (1/0)—[c2mmL (1/1)—p2ggL (1/1.33)] p4gmL (1/3)—CLQC (1/3.15) (see Figure 9 and Table S10). The ratios in parentheses indicate the ratio of strongly elliptical alkyl chain columns acting as honeycomb walls to the (almost) circular columns interconnecting the p-terphenyl walls at the remaining nodes. We note that for p2ggL each wall separating two pentagons is counted as a single elliptical node and for CLQC this ratio depends on the number of inflations (see Table S10).
Based on the tilings depicted in Figure 9a–g, the curves of the averaged A/C ratios in each mesophase versus the effective side length (Leff), which depends on the alkyl chain stretching, are plotted in Figure 9j, see details in Section S4.4. Two different types of curves can be recognized: rapid increasing for the ordinary honeycombs p2gg and p4gm and almost horizontal and parallel lines for the CLQC and its approximant supertilings. For the honeycombs of the p2gg and p4gm phase, the A/C ratio directly determines the phase structure according to the volume of EO chain, i.e., controlled by steric effect. However, for the CLQC and its approximants, the A/C ratio decreases from c2mmL via the higher generation CLQC to the p4gmL phase, suggesting the participation of extra effects. Interestingly, the A/C ratio of the CLQC phase decreases and convergences towards the line of the p4gmL phase with growing number of inflations (starting with the second generation, see Table S11), which might be considered as a driving force behind the development of high perfection of the quasicrystalline order. Hence, it appears that the long range CLQC and the periodic p4gmL lattice can both achieve an optimal A/C ratio. The more equalized tile size in CLQC and its approximants is further beneficial for vibrational entropy gain (see Figure S29). Although the configurational entropy does not change at the transition from p4gmL to CLQC, the vibrational entropy (phase space volume that the nodes with fixed bond around their lattice positions can explore)17 as well as the conformational alkyl chain entropy (see above) do increase at this transition. Thus, the subtle interplay between enthalpy and (conformational & vibrational) entropy leads to the dominance of the CLQC phase at high temperature by suppressing the competing periodic p4gmL phase at the cross-over from p2gg to p4gm. More generally, the balance between steric and entropic effects leads to the generation of structural complexity and quasiperiodicity in ordered soft matter.
In addition, kinetic effects play an important role for the phase sequence actually observed depending on sample history and heating/cooling rate (Figure 2), and appears to be a result of the different flexibility of the honeycombs. The p2gg, p4gm, p4gmL and CLQC phases form spherulitic and fan-like POM textures as typical for soft columnar phases which can easily bend (Figures 3a, S7a,b, S8a–d, S9, S10); the phase transitions between these soft honeycombs are almost reversible and only small hysteresis effects can be observed. In contrast, c2mmL and p2ggL form mosaic-like textures (Figures S7c,d,g, S8e), indicating relatively rigid honeycombs, for which slow transitions and significant hysteresis effects are typically observed, which suppressed the p2ggL phase upon cooling. Thus, the different softness of the honeycombs leads to the different phase sequences depending on heating/cooling rates (Figure 2). Though the precise origin of this difference is unknown, it appears that c2mmL and p2ggL with parallel aligned “fat” octagons allow an overall denser packing, than the perpendicularly aligned tighter octagons in p4gmL and CLQC, which might be affected by the degree of fusion of the trapezoidal cells (see Figures 10c–e, 11a and discussion below).
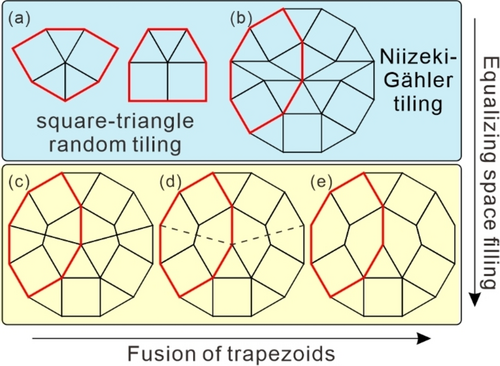
Schematic representations showing the basic motifs of dodecagonal 2D tilings: a) commonly observed motifs in the “random” triangle-square Stampfli tiling; b) the dodecagonal Niizeki-Gähler tiling involving thin rhombs in the octagonal motifs; long-range CLQC tilings: c) containing pairs of trapezoids as reported before10 and d) with partly fused trapezoids as reported herein; e) potential CLQC tiling involving pentagons formed by the fusion of pairs of trapezoids.
If compared with other quasicrystalline tessellations, the introduction of trapezoids into the dodecagonal square-triangle tessellation (Stampfli-tiling)18 provides a transition from random to strict quasiperiodicity. Figure 10 illustrates the transition from the random Stampfli tiling (Figure 10a) to the strictly quasiperiodic triangle-square-trapezoid tiling (Figure 10c) by replacing the 3 triangles with 4 trapezoids and simultaneously expanding the local irregular supertile motifs to octagons. Octagons in Figure 10c could also be considered as derived from the octagonal motif of the Niizeki-Gähler tiling (Figure 10b)19 by removing the thin rhombi, thus improving equal space filling. Tilings in Figure 10a,b were previously observed as local structures of solid-state 2D nets on surfaces12e, 20 and the random tiling in Figure 10a was found in a polymer morphology,12a, 12c whereas Figure 10c is the tiling of the CLQC.
Moreover, fusing pairs of trapezoids into pentagons as in Figure 10e leads to an additional quasiperiodic tiling derived from (c), where the A/C ratio of the pentagon (0.26) is very close to squares (0.25). Such a pentagon-containing tiling also follows a strict inflation rule (see Figure S30).
Comparing the SAXS pattern of 12/5 with the previously reported CLQC of compound A16/6 with ionic end groups at the side chains,10 12/5 exhibits a significant enhancement of the (2100) peak, making it the second strongest SAXS signal (see Section S4.5 and Table S16). Though (2100) is weak, it is of strong influence on the ED distribution within the pairs of trapezoids in the reconstructed ED maps (see Figures 11 and S31). The reduction of the ED gap around the walls separating the trapezoidal cells in p4gmL and CLQC indicates a partial mixing of side chains and terphenyl rods, which can be interpreted either by a reduction of the number of terphenyls forming these inter-trapezoidal walls, or by a time and space averaging of some trapezoid pairs to pentagons. Because the long-range order is retained the first option is more likely. Compared to the ionic end group of compound A16/6, the glycerol end group of 12/5 provides a reduced degree of chemical incompatibility with the terphenyls, allowing a higher degree of partial mixing, thus leading to more diffuse inter-materials interfaces and allowing a partial fusion of the pairs of trapezoidal cells to pentagons. Such fusion is also supported by the different aspect ratios of the octagons in the different phases. In the c2mmL phase of 12/5 where the pentagons are supposed to be fully divided into trapezoids, there is a “fat” octagonal motif. Partial fusion with reduction of the number of side-by-side arranged terphenyls in the walls dividing the trapezoids is required to shrink the size of alkyl domains between the trapezoids, leading to “thin” octagons in p4gmL and CLQC (Figure 11a). In contrast, for A16/6, “thin” octagons with fully divided trapezoids are already present in p4gmL and CLQC, thus prohibit the formation of “fat” octagons (Figure 11b). This partial fusion to larger pentagons in the case of 12/5 is additionally supported by the slightly larger effective volume fraction of the lateral chains of 12/5 compared to A16/6 which can be deduced from the replacement of the triangular lowest temperature honeycomb of A16/6 (ColhexΔ, Scheme 2) by those involving larger trapezoidal (p2gg and c2mmL) for 12/5 (Figures 1 and 2).
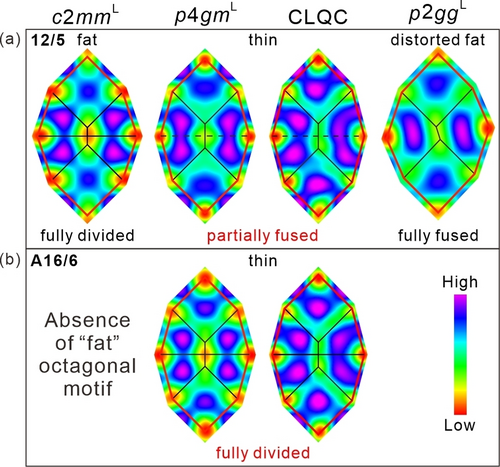
Octagonal motifs of CLQC and its approximants of a) 12/5 reported herein and b) A16/6 reported before.10 The partially fused trapezoids in p4gmL and CLQC are indicated by dashed lines (see Figure S31 for details).
In the complex p2ggL lattice the dividing walls are completely removed leading to truly pentagonal cells (see Figures 7b,c and 11a). This structure can be considered as an approximant of the quasiperiodic tiling based on pentagonal tiles in Figure 10e, which might be uncovered in future work by proper chemical design of further optimized tethered rods.
Overall, in the CLQC phase of 12/5 and its p4gmL approximant the walls dividing the pentagons are still retained, but thinner than the others (see Figure 11a) which is indicated by dashed lines in Figure 10d and makes them distinct from those previously reported for A16/6 (Figure 10c).10
Conclusion
In conclusion, we have shown that the formation of CLQCs is a general new feature of T-shaped facial polyphiles during the transition from triangular to square honeycombs upon side chain expansion. More specifically, the CLQC and its approximants fall between the trapezoidal and the square+triangle tiling.
Combination of trapezoidal, square and triangular tiles results in octagonal motifs comprising two squares and four trapezoids. The trapezoids optimize the local packing and allow a strictly quasiperiodic tessellation, whereas the stability of previous dodecagonal soft quasicrystals—involving only regular triangles and squares—was based on the configurational entropy of randomness.
Along with the CLQC phase, periodic approximants based on this octagonal supertiling motif are also observed, following a temperature dependent sequence Cr—p2gg—[c2mmL—p2ggL]—p4gmL—CLQC—Iso. The key requirement for the formation of this unique series of complex mesophases is the temperature dependent change in the alkyl chain stiffness, which leads to an elliptical deformation of the non-polar alkyl chain columns, allowing the formation of trapezoidal cells with intermediate A/C ratio between squares and triangles. However, the competing enthalpic and entropic effects arising from the chain ordering and the core expansion due to chain stiffening result in complex relationships that force the 2D network to assume a series of periodic supertilings and even a quasiperiodic tiling pattern.
This work uncovers the rich variety of 2D liquid (quasi)crystal phases based on the special trapezoidal tile and suggests the existence of CLQC with partly or fully fused trapezoid pairs. Reports on trapezoid-based quasiperiodic tiling patterns with decagonal21 or octagonal symmetry22 raise the question if the trapezoid and its variants could in the future lead to CLQC materials with other than 12-fold symmetries.
Overall, this research is expected to stimulate further understanding of general aspects of quasiperiodicity formation and its relation to the molecular structure of non-spherical molecules and supramolecular aggregates, and to pave the way to even more new CLQCs and their periodic approximant LCs. Such soft CLQCs could lead to potential applications, for example, as self-healing and responsive materials for soft nano-lithography and photonics.4b, 23 Moreover, the developed fundamental concepts could also be applied to other fields, as for example to achieve quasiperiodicity in reticular chemistry based solid-state systems like hydrogen bonded, metal-organic and covalent organic frameworks (MOFs and COFs).24
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 21761132033, 21374086, 11922410 and 12204369), Science and Technology Agency of Shaanxi Province (2023-YBGY-459), China Postdoctoral Science Foundation (2022M712551, 2023T160505) and the Deutsche Forschungsgemeinschaft (DFG, 436494874-GRK 2670). We also thank beamline BL16B1 at Shanghai Synchrotron Radiation Facility for providing beamtimes. Part of the characterization was performed at Instrument Analysis Center of Xi'an Jiaotong University. We thank Prof. Huijun Zhang from Xi'an Jiaotong University for fruitful discussion. Open Access funding enabled and organized by Projekt DEAL.
Conflict of interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available in the Supporting Information. Metadata are available from the corresponding author upon reasonable request.