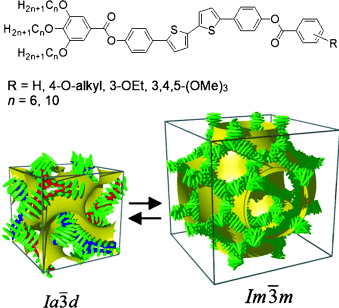
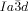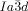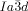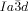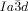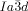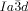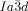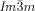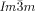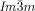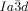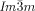Dynamic Mirror-Symmetry Breaking in Bicontinuous Cubic Phases†
We acknowledge financial support from the government of Saxonia-Anhalt through the Cluster of Excellence “Nanostructured Materials”, DFG (FG 1045, TS 39/21-2), from NSF-EPSRC Pire program RENEW (EP/K034308), the Leverhulme Foundation (RPG-2012-804), the National Natural Science Foundation of China (No. 21374086), and the 1000 Talents Program of P.R. China. For help and advice with CD experiments we thank Prof. G. Siligardi and Drs. R. Hussain and T. Javorfi of B23 at Diamond Light Source; for help with X-ray synchrotron experiments we thank Drs. D. Wermeille, S. Brown and P. Thompson of the XMaS beamline at ESRF, Dr. Steve Collins of I16 and Prof. N. Terrill of I22 at Diamond.
Graphical Abstract
Cubics with a twist: Polycatenar 5,5′-diphenyl-2,2′-bithiophenes (see picture) form two types of bicontinuous cubic phases. Though the molecules are achiral the  cubic phase is always chiral, while the
cubic phase is always chiral, while the 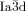 phase is achiral. The explanation is that in the
phase is achiral. The explanation is that in the 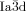 phase the opposing chiralities of the two enantiomorphic networks cancel, but not so in the three-network
phase the opposing chiralities of the two enantiomorphic networks cancel, but not so in the three-network 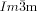 phase.
phase.
Abstract
Chiral segregation of enantiomers or chiral conformers of achiral molecules during self-assembly in well-ordered crystalline superstructures has fascinated chemists since Pasteur. Here we report spontaneous mirror-symmetry breaking in cubic phases formed by achiral multichain-terminated diphenyl-2,2′-bithiophenes. It was found that stochastic symmetry breaking is a general phenomenon observed in bicontinuous cubic liquid crystal phases of achiral rod-like compounds. In all compounds studied the 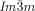 cubic phase is always chiral, while the
cubic phase is always chiral, while the 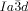 phase is achiral. These intriguing observations are explained by propagation of homochiral helical twist across the entire networks through helix matching at network junctions. In the
phase is achiral. These intriguing observations are explained by propagation of homochiral helical twist across the entire networks through helix matching at network junctions. In the 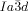 phase the opposing chiralities of the two networks cancel, but not so in the three-networks
phase the opposing chiralities of the two networks cancel, but not so in the three-networks 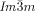 phase. The high twist in the
phase. The high twist in the 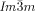 phase explains its previously unrecognized chirality, as well as the origin of this complex structure and the transitions between the different cubic phases.
phase explains its previously unrecognized chirality, as well as the origin of this complex structure and the transitions between the different cubic phases.
Design and investigation of chiral self-assembled superstructures represents a fascinating field of contemporary research which provides numerous potential applications. Beside enantiomeric mixtures of molecules, segregation of chiral supermolecular aggregates,1, 2, 3 and chiral molecular conformations were also found as sources of macroscopic chirality in the crystalline state and at surfaces.4 In recent years interest in mirror-symmetry breaking extended to soft matter systems. Special progress in this field was made with liquid crystalline phases formed by bent-core molecules and bent-shaped mesogenic dimers showing symmetry breaking in their lamellar5–11 and nematic phases, respectively.12, 13 Spontaneous formation of helical superstructures was also observed in soft columnar crystals at reduced temperature where packing density is increased and the mobility of the aromatic segments is reduced.14–17 The lateral coupling between columns is much weaker than the longitudinal, therefore macroscopic chiral segregation is usually not observed, except for one case.10 Though, there is one report about spontaneous stochastic symmetry breaking in a thermotropic cubic phase, the structure of this cubic phase and the possible origin of macroscopic chirality are not clear in this case.18
Herein we report that stochastic symmetry breaking is a general phenomenon typically observed in the bicontinuous cubic phases of achiral rod-like and polycatenar (multichain-terminated) liquid crystalline (LC) compounds.19 We show that optical activity and circular dichroism (CD) develop spontaneously whenever the cubic phase is of the triple-network type with 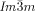 symmetry20, 21 whereas, in contrast, the “double gyroid”
symmetry20, 21 whereas, in contrast, the “double gyroid” 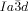 cubic phase always remains achiral. These observations are explained by the action of two newly recognized phenomena: a) the correlated helical twist of molecular axis in the segments of the infinite interpenetrating networks, and b) the percolation through mm-sized domains of uniform helical sense carried across the network through matching of molecular orientation twist sense at network junctions. The current findings also bring the understanding of thermotropic cubic phases to a qualitatively new level and contribute to the general appreciation of symmetry breaking in LCs of achiral molecules.
cubic phase always remains achiral. These observations are explained by the action of two newly recognized phenomena: a) the correlated helical twist of molecular axis in the segments of the infinite interpenetrating networks, and b) the percolation through mm-sized domains of uniform helical sense carried across the network through matching of molecular orientation twist sense at network junctions. The current findings also bring the understanding of thermotropic cubic phases to a qualitatively new level and contribute to the general appreciation of symmetry breaking in LCs of achiral molecules.
The compounds under investigation (compounds 1, see Table 1) represent polycatenar rod-like molecules based on a 5,5′-diphenylbithiophene core (for synthesis, see the Supporting Information (SI)).23 Crystalline phases of compounds 1 melt between 110 and 139 °C and form optically isotropic and highly viscous mesophases which, based on X-ray diffraction (XRD) evidence (see below), are cubic LC phases, and which on further rising temperature transform to isotropic liquids. In some cases, an additional liquid-liquid transition (LLT) is observed and the liquid phase occurring between the cubic and the “ordinary” isotropic liquid is labelled here IsoLT, the liquid phase at higher temperature as IsoHT. IsoLT phases have previously been found as intermediate phases at Cub-Iso transitions (labelled Iso1)22 and have recently been found to be chiral in some cases, representing a conglomerate of two segregated enantiomeric liquids (Iso1[*]).23 This chiral IsoLT is denoted here as IsoLT[*]. While IsoLT[*] appears in 1 d both on heating and cooling,23 in 1 b and 1 e it occurs only on cooling (monotropic phase). Compounds 1 a, 1 c, 1 f and 1 g form the cubic phases directly from the achiral IsoHT. Sharp DSC peaks accompany Cub-Iso transitions on heating and IsoHT-Cub transitions on cooling, but the IsoHT-IsoLT[*] exotherm is broad and is better described as a heat capacity anomaly rather than a first-order transition (see Figure 3 c,d, Table 1 and Figures S1–S9 in the SI).
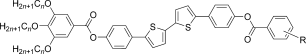
|
Compd. |
n |
R |
Phase transitions on heating/cooling (T/°C) |
acub [nm] |
|---|---|---|---|---|
|
1 a |
10 |
H |
Cr 114 [39.7] Cub/ |
10.8 |
|
1 b |
10 |
4-OCH3 |
Cr 119 [55.3] Cub/ |
11.4 |
|
1 c |
10 |
3,4-(OCH3)2 |
Cr 137 [44.6] Cub/ |
11.1 |
|
1 d23 |
6 |
4-OC6H13 |
Cr 139 [55.2] M 171 [-] Cub/ |
10.3 |
|
1 e |
10 |
4-OC10H21 |
Cr 134 [49.9] Cub[*]/ |
17.9 |
|
1 f |
10 |
3-OC2H5 |
Cr 100 [27.8] Cub[*]/ |
15.7 |
|
1 g |
10 |
3,4,5-(OCH3)3 |
Cr 110 [70.2] Cub[*]/ |
15.4 |
-
[a] Abbreviations: Cr=crystalline solid, Cub/
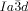 =bicontinuous cubic phase with
=bicontinuous cubic phase with 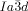 lattice (achiral); Cub[*]/
lattice (achiral); Cub[*]/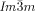 =chiral conglomerate cubic phase with
=chiral conglomerate cubic phase with 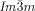 lattice; IsoLT[*]=chiral isotropic liquid phase formed by a conglomerate of domains with opposite handedness; IsoHT=achiral isotropic liquid phase.
lattice; IsoLT[*]=chiral isotropic liquid phase formed by a conglomerate of domains with opposite handedness; IsoHT=achiral isotropic liquid phase.
Cubic space groups were determined by powder small-angle XRD and grazing-incidence diffraction as shown in the SI (Figures S11, S12, and Tables S2–S8). Two cubic phases were observed, the double-network “gyroid”, with 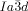 symmetry (Figure 1 a), and the triple-network phase with
symmetry (Figure 1 a), and the triple-network phase with 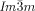 symmetry (Figure 1 b). The lattice parameters of the cubic phases are in the typical ranges around acub=11 nm for the
symmetry (Figure 1 b). The lattice parameters of the cubic phases are in the typical ranges around acub=11 nm for the 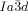 phase and acub=15–18 nm for the
phase and acub=15–18 nm for the 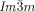 phase.
phase.
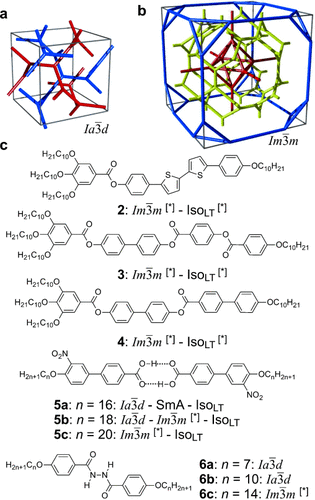
a,b) Framework models of a unit cell of the two cubic structures discussed in this work20 (see also Figures S15 and S16) and c) typical chemical structures of representative compounds forming these phases (compounds 2–4 were newly synthesized, as described in the SI, and compounds 5 and 6 were known from literature, see Table S1 and Figures S7–S9, S13, S14, S17–S22 for details.19 a) The double-network 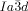 (“gyroid”) phase; b) the triple-network
(“gyroid”) phase; b) the triple-network 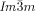 phase. Each of the infinite networks is coloured differently. In (b) the red and blue are the identical “inner” and “outer” networks, mutually related by a (1/2 1/2 1/2) translation; yellow is the “middle” network. Equivalent figures with the added minimum surface are shown in SI.
phase. Each of the infinite networks is coloured differently. In (b) the red and blue are the identical “inner” and “outer” networks, mutually related by a (1/2 1/2 1/2) translation; yellow is the “middle” network. Equivalent figures with the added minimum surface are shown in SI.
Symmetry breaking is observed in some of the cubic phases by polarized microscopy if the analyzer is rotated by a small angle out of the 90 °C crossed position with respect to the polarizer. In this way the polarizing microscope can be used as a polarimeter with the additional advantage of spatial resolution. Remarkably, all 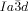 cubic phases of the investigated compounds are optically inactive, whereas for all
cubic phases of the investigated compounds are optically inactive, whereas for all 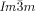 phases darker and brighter domains become visible between slightly uncrossed polarizers, which exchange their contrast if the rotation of the analyzer is reversed (Figure 2 a,b). Rotating the sample between the polarizers does not change the contrast. This means that the
phases darker and brighter domains become visible between slightly uncrossed polarizers, which exchange their contrast if the rotation of the analyzer is reversed (Figure 2 a,b). Rotating the sample between the polarizers does not change the contrast. This means that the 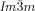 phase represents a conglomerate of chiral domains with opposite handedness. Thus this cubic phase is denoted Cub[*]/
phase represents a conglomerate of chiral domains with opposite handedness. Thus this cubic phase is denoted Cub[*]/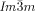 .24
.24

Photomicrographs of chiral domains (dark/bright), observed between slightly uncrossed polarizers. The orientations of polarizer (P) and analyzer (A) are indicated by arrows. a,b) 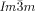 phase of compound 1 f at T=112 °C as obtained on cooling from the achiral IsoHT phase, c) IsoLT[*] phase of compound 1 e (T=177 °C) and d)
phase of compound 1 f at T=112 °C as obtained on cooling from the achiral IsoHT phase, c) IsoLT[*] phase of compound 1 e (T=177 °C) and d) 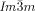 phase (T=175 °C) as observed after transition from the IsoLT[*] phase; note that the domain boundaries between the chiral domains are slightly shifted. e,f) Growths of the domains of the
phase (T=175 °C) as observed after transition from the IsoLT[*] phase; note that the domain boundaries between the chiral domains are slightly shifted. e,f) Growths of the domains of the 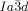 phase at the IsoLT[*]-
phase at the IsoLT[*]-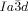 transition as observed for compound 1 b at T=160 °C (white arrow indicates a seed of the
transition as observed for compound 1 b at T=160 °C (white arrow indicates a seed of the 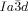 phase); note that during formation of the cubic phase the chirality of the IsoLT[*] phase is completely extinguished (see also videos in SI).
phase); note that during formation of the cubic phase the chirality of the IsoLT[*] phase is completely extinguished (see also videos in SI).
Microbeam circular dichroism (CD) spectroscopy confirmed the presence of chiral domains in the 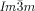 phase. Figure 3 a shows the CD evolution with temperature during heating a bulk film of 1 g from the Cub[*]/
phase. Figure 3 a shows the CD evolution with temperature during heating a bulk film of 1 g from the Cub[*]/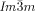 (120–125 °C) to the IsoHT phase (130–140 °C), and then cooling back to the Cub[*]/
(120–125 °C) to the IsoHT phase (130–140 °C), and then cooling back to the Cub[*]/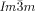 (120–125 °C, dashed curves). As can be seen, there is strong CD in the cubic phase, disappearing in the isotropic IsoHT liquid and reappearing in the Cub[*]/
(120–125 °C, dashed curves). As can be seen, there is strong CD in the cubic phase, disappearing in the isotropic IsoHT liquid and reappearing in the Cub[*]/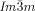 , this time either with the same or with reversed chirality. In contrast, on no occasion did the Cub/
, this time either with the same or with reversed chirality. In contrast, on no occasion did the Cub/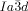 phase give any measurable CD.
phase give any measurable CD.
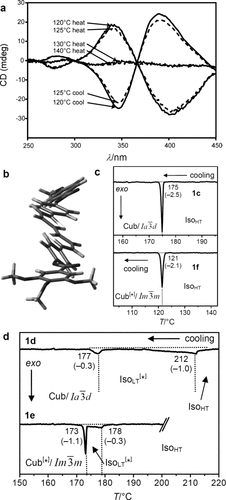
a) Temperature dependent CD spectra (ellipticity in mdeg) of a bulk film of compound 1 g in the Cub[*]/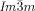 (120–125 °C) and the IsoHT liquid (130–140 °C). On cooling back to the Cub[*]/
(120–125 °C) and the IsoHT liquid (130–140 °C). On cooling back to the Cub[*]/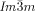 (dashed curves) chirality reverses. b) Helical conformations as computed for a model compound related to compounds 1 b,e with OCH3 groups instead of the long alkyloxy chains.23 c,d) DSC cooling thermograms of c) 1 c and 1 f with direct IsoHT-Cub transitions and d) 1 d23 and 1 e with an intermediate IsoLT[*] phase (see also Figures S1–S6).
(dashed curves) chirality reverses. b) Helical conformations as computed for a model compound related to compounds 1 b,e with OCH3 groups instead of the long alkyloxy chains.23 c,d) DSC cooling thermograms of c) 1 c and 1 f with direct IsoHT-Cub transitions and d) 1 d23 and 1 e with an intermediate IsoLT[*] phase (see also Figures S1–S6).
While both, optical activity and CD, are strongly affected by helical order, CD is highly sensitive to molecular conformation. It is suggested that the chiral chromophore mainly responsible for the CD is the slightly twisted 5,5′-diphenyl-2,2′-bithiophene unit (Figure 3 b) which has its UV absorption maximum at the inflection point of the CD curves at 374 nm (Figure S10).
As mentioned above, there are two different types of transitions from the achiral IsoHT liquid to the Cub[*]/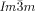 phase, either directly (compounds 1 f and 1 g, Figure 2 a,b) or via the chiral IsoLT[*] phase (compounds 1 e and 2, Figure 2 c,d). The chirality of the IsoLT[*] phase, a conglomerate of chiral domains, is indicated by optical investigations in the same way as described for the cubic phases (see Figure 2 c). Where the transition takes place directly from the achiral IsoHT phase the resulting chiral domains have mainly straight boundaries reflecting crystallographic facets (Figure 2 a,b). However, when the
phase, either directly (compounds 1 f and 1 g, Figure 2 a,b) or via the chiral IsoLT[*] phase (compounds 1 e and 2, Figure 2 c,d). The chirality of the IsoLT[*] phase, a conglomerate of chiral domains, is indicated by optical investigations in the same way as described for the cubic phases (see Figure 2 c). Where the transition takes place directly from the achiral IsoHT phase the resulting chiral domains have mainly straight boundaries reflecting crystallographic facets (Figure 2 a,b). However, when the 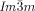 phase grows from the already chiral IsoLT[*] phase, the chiral cubic domain boundaries follow closely the curved borders between the enantiomeric liquid domains of the IsoLT[*] phase (see Figure 2 c,d and Video 1e on the SI website).
phase grows from the already chiral IsoLT[*] phase, the chiral cubic domain boundaries follow closely the curved borders between the enantiomeric liquid domains of the IsoLT[*] phase (see Figure 2 c,d and Video 1e on the SI website).
The transition to the 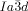 phase can also occur in two ways. Other than by XRD, the direct transition IsoHT-Cub/
phase can also occur in two ways. Other than by XRD, the direct transition IsoHT-Cub/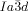 is only detectable by a marked increase in viscosity (compounds 1 a and 1 c). In this case investigation between uncrossed polarizers give no evidence of chirality. What is more, where the
is only detectable by a marked increase in viscosity (compounds 1 a and 1 c). In this case investigation between uncrossed polarizers give no evidence of chirality. What is more, where the 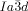 is formed from the chiral IsoLT[*] phase (compounds 1 b and 1 d), the chirality is completely erased (see Figure 2 e,f).
is formed from the chiral IsoLT[*] phase (compounds 1 b and 1 d), the chirality is completely erased (see Figure 2 e,f).
Similar IsoLT[*]-Cub[*]/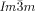 transition behavior as for compound 1 e, was also observed for compound 2, having a shorter bithiophene unit and for the tetracatenar compounds 3 and 4 without the bithiophene units. 5 (ANBC-n) and 6 (BABH-n) are members of the two best investigated homologous series of cubic phase forming compounds (see Table S1 and Figures 1, S7–S9, S13, S14, S17–S22).19, 25 Remarkably, also for these compounds in all cases the
transition behavior as for compound 1 e, was also observed for compound 2, having a shorter bithiophene unit and for the tetracatenar compounds 3 and 4 without the bithiophene units. 5 (ANBC-n) and 6 (BABH-n) are members of the two best investigated homologous series of cubic phase forming compounds (see Table S1 and Figures 1, S7–S9, S13, S14, S17–S22).19, 25 Remarkably, also for these compounds in all cases the 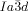 phase is achiral (compounds 5 a, b and 6 a, b) whereas the
phase is achiral (compounds 5 a, b and 6 a, b) whereas the 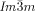 phase appears as chiral conglomerate (compounds 2–4, 5 b, c and 6 c). For the 3′-nitro-4′-alkoxybiphenyl carboxylic acids 5 there is an additional enantiotropic (i.e. reversible) IsoHT–IsoLT transition; however in this case the IsoLT phase is for all investigated compounds achiral. Nevertheless, chirality evolves for 5 c (n=20) at the transition to the Cub[*]/
phase appears as chiral conglomerate (compounds 2–4, 5 b, c and 6 c). For the 3′-nitro-4′-alkoxybiphenyl carboxylic acids 5 there is an additional enantiotropic (i.e. reversible) IsoHT–IsoLT transition; however in this case the IsoLT phase is for all investigated compounds achiral. Nevertheless, chirality evolves for 5 c (n=20) at the transition to the Cub[*]/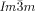 phase (see Table S1 and Figure S20e,f). For 5 b (n=18) an achiral
phase (see Table S1 and Figure S20e,f). For 5 b (n=18) an achiral 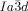 phase is formed on cooling, but on heating an additional
phase is formed on cooling, but on heating an additional 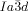 –
–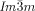 transition occurs at T≈180 °C (Figure S20c,d).19 Again, chiral domains invariably appear at this transition. Thus, the Cub/
transition occurs at T≈180 °C (Figure S20c,d).19 Again, chiral domains invariably appear at this transition. Thus, the Cub/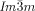 phase was found to be chiral in all these diverse non-chiral polycatenar compounds, without exception,24 while the Cub/
phase was found to be chiral in all these diverse non-chiral polycatenar compounds, without exception,24 while the Cub/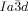 was non-chiral, also without exception. Hence, chirality of the
was non-chiral, also without exception. Hence, chirality of the 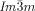 phases appears to be a general phenomenon, already present in long known systems, but surprisingly not previously recognized.26 Chirality in the Cub[*]/
phases appears to be a general phenomenon, already present in long known systems, but surprisingly not previously recognized.26 Chirality in the Cub[*]/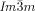 phase has thus been seen to develop in four different ways, either 1) directly from the achiral isotropic liquid IsoHT, via IsoLT phases which can be either 2) chiral (IsoLT[*]) or 3) achiral (IsoLT), or 4) from the achiral Cub/
phase has thus been seen to develop in four different ways, either 1) directly from the achiral isotropic liquid IsoHT, via IsoLT phases which can be either 2) chiral (IsoLT[*]) or 3) achiral (IsoLT), or 4) from the achiral Cub/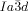 phase.
phase.
For the understanding of the development of chirality in the cubic phase it must be recalled that the molecules have liquid like local order, with no hint of any Bragg-like X-ray reflection in the wide-angle range. Therefore, the classical approach of achiral symmetry breaking, where the formation of a more or less ordered crystalline phase energetically favors one chiral conformer over another,1, 3, 7 cannot be applied here. Considering that the observed “static symmetry breaking” leads to a significant entropy penalty, there is a compelling mode of self-assembly that compensates for the entropy loss, yet does not involve crystallization at any level (“dynamic symmetry breaking”), as introduced recently as the underlying process for mirror-symmetry breaking in isotropic liquids.23 The model must also explain why all Cub/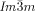 phases are chiral and all Cub/
phases are chiral and all Cub/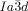 ones are not.
ones are not.
In soft-crystal columns of short hexacatenar hydrazine rods27 or broader board-like perylene bisimides28 it was found that molecular pairs stack on top of one another with a nearly 90° twist. In this way the molten alkyls spread around the column while effective core–core π-stacking is still maintained. For long thin rods with less than six chains, as studied here, a smaller twist angle would be sufficient to alleviate the crowding of the alkyls,19, 29 thus allowing the development of helical twist. Without any degree of 3D positional order of achiral molecules, as in the “disordered” hexagonal columnar LC phase, there is no long-range helical order (LRHO). However, the superstructural twist couples with the helical twist of the chiral molecular conformations, thus biasing each other and collectively favoring the helical superstructure in the fluid columns.23 Thus, the preorganization in columns favors conformational segregation and vica verse. But even in this case, in 1D columns, without intercolumnar correlation, a helix reversal defect has no way of being corrected, so that macroscopic chirality cannot be observed in fluid columnar LC phases.
However, in the bicontinuous cubic phases we also must consider the network junctions. At the 3-fold junctions the three twisting “ribbons” that may be used to represent the network segments, must merge into one another smoothly. In an optimal junction the aromatic rods arrive parallel to each other and with a synchronized twist where the helices lock-in together as they approach each other—for the 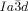 network junction (see Figure 4 b,c). The junction itself then effectively becomes a small triangular platelet, approximately normal to the molecular axis.19, 25 We calculate that there is a distance of 0.345 acub≈3.9 nm between the junctions, which accommodates about 9 molecular triplets spaced at 0.45 nm. As the twist between the
network junction (see Figure 4 b,c). The junction itself then effectively becomes a small triangular platelet, approximately normal to the molecular axis.19, 25 We calculate that there is a distance of 0.345 acub≈3.9 nm between the junctions, which accommodates about 9 molecular triplets spaced at 0.45 nm. As the twist between the 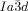 junctions is ϕ=±70.5°, there is an average rotation of ±8° between adjacent molecules. For details see SI. As is well known, the two networks in the
junctions is ϕ=±70.5°, there is an average rotation of ±8° between adjacent molecules. For details see SI. As is well known, the two networks in the 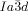 phase have opposite chirality; the blue network in Figures 1 a and 4 a is right-handed and the red network is left-handed. Thus, although there is long-range helical order in each of the two interpenetrating infinite networks of the
phase have opposite chirality; the blue network in Figures 1 a and 4 a is right-handed and the red network is left-handed. Thus, although there is long-range helical order in each of the two interpenetrating infinite networks of the 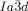 phase, there is no net chirality as the two cancel completely. Figure 4 a gives an impression of the proposed
phase, there is no net chirality as the two cancel completely. Figure 4 a gives an impression of the proposed 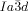 structure, including the minimum surface that separates the two networks (see also SI).
structure, including the minimum surface that separates the two networks (see also SI).
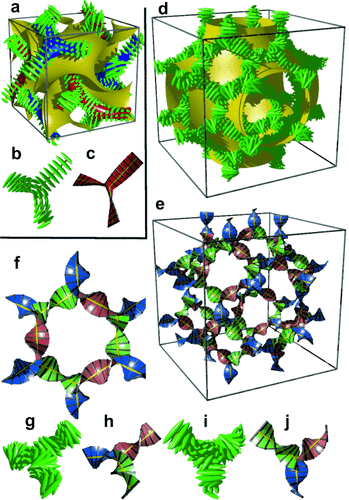
a) The two networks (red and blue) of the  phase decorated with schematic mesogens (rod-like molecular cores, green) showing the molecular twist along the network segments. The gyroid minimum surface is also shown (yellow) and b,c) show the network junctions. d) The same for the middle of the three networks of the
phase decorated with schematic mesogens (rod-like molecular cores, green) showing the molecular twist along the network segments. The gyroid minimum surface is also shown (yellow) and b,c) show the network junctions. d) The same for the middle of the three networks of the  phase (yellow network in Figure 1 b). This network closely follows the Schwartz P-type minimum surface (shown in yellow). e) The middle
phase (yellow network in Figure 1 b). This network closely follows the Schwartz P-type minimum surface (shown in yellow). e) The middle 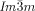 network shown as ribbons containing the molecular axes axis (black rods) and f) loop of 6 junctions in this network. g–j) Details of the two types of junctions in the
network shown as ribbons containing the molecular axes axis (black rods) and f) loop of 6 junctions in this network. g–j) Details of the two types of junctions in the 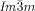 phase in mesogen (g,i) and ribbon (h,j) representations.
phase in mesogen (g,i) and ribbon (h,j) representations.
Turning to the 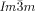 phase, this contains three rather than two networks,20, 21 a fact on which we base our explanation of its chirality. Examination of the three networks in Figure 1 b shows that they are not intrinsically chiral. However, it is reasonable to assume that they also contain molecular twist as in the
phase, this contains three rather than two networks,20, 21 a fact on which we base our explanation of its chirality. Examination of the three networks in Figure 1 b shows that they are not intrinsically chiral. However, it is reasonable to assume that they also contain molecular twist as in the 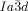 phase. In fact even more so, as the molecules displaying the
phase. In fact even more so, as the molecules displaying the 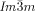 phase (e.g. 1 e–1 g) generally have larger terminal groups than
phase (e.g. 1 e–1 g) generally have larger terminal groups than 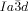 -forming compounds (e.g. 1 a–1 d). They are thus expected to cause greater steric crowding. We concentrate here only on the middle (yellow) network, as it is the simplest of the three and, like in the
-forming compounds (e.g. 1 a–1 d). They are thus expected to cause greater steric crowding. We concentrate here only on the middle (yellow) network, as it is the simplest of the three and, like in the 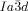 phase, contains only 3-way junctions. The key assumption is, as with the
phase, contains only 3-way junctions. The key assumption is, as with the 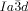 phase, that at the junctions, in order to interlock smoothly, the molecules twist with the same sense. As an example, a portion of the middle network forming a closed loop of 6 junctions is shown in the ribbon representation in Figure 4 f. There are three “perfect” (I) and three “imperfect” (II) junctions in that loop, detailed in Figures 4 g,h and i,j, respectively. In junctions I all ribbons merge perfectly smoothly, while in junctions II the blue and red ribbons merge smoothly but the green comes at an angle. We note that the latter defect is of little consequence because even if all green segments were disconnected, the remaining network would still remain connected and percolating the entire domain of the phase. The full extent of the middle network within the unit cell is shown in Figures 4 d,e,, with the Schwartz P minimum surface added in Figure 4 d. A calculation similar to that for the
phase, that at the junctions, in order to interlock smoothly, the molecules twist with the same sense. As an example, a portion of the middle network forming a closed loop of 6 junctions is shown in the ribbon representation in Figure 4 f. There are three “perfect” (I) and three “imperfect” (II) junctions in that loop, detailed in Figures 4 g,h and i,j, respectively. In junctions I all ribbons merge perfectly smoothly, while in junctions II the blue and red ribbons merge smoothly but the green comes at an angle. We note that the latter defect is of little consequence because even if all green segments were disconnected, the remaining network would still remain connected and percolating the entire domain of the phase. The full extent of the middle network within the unit cell is shown in Figures 4 d,e,, with the Schwartz P minimum surface added in Figure 4 d. A calculation similar to that for the 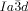 phase (details in SI) gives the average twist angle between adjacent molecules as 30–35°, that is, significantly higher than the value for the
phase (details in SI) gives the average twist angle between adjacent molecules as 30–35°, that is, significantly higher than the value for the 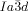 phase, and in line with the expectation.
phase, and in line with the expectation.
A similar calculation can be performed on the other two networks; however because of their complexity we shall not discuss them here. The important point to make, however, is that the chirality of the middle network will undoubtedly affect the chirality of the inner and outer networks. Because of their crystallographic equivalence, the helical sense of the inner and outer (red and blue) network will be the same. Whether it will be the same or opposite of that of the middle network, we cannot tell with certainty. However, what is certain is that, in the general case, there will always be at least a residual chirality in the cubic 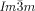 phase, as indeed observed.
phase, as indeed observed.
The above model implies that each of the cubic structures is the solution best suited to accommodate a certain range of required molecular twist angles. It is not suggested that the 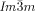 provides a general solution for any situation that requires high twist. In fact experiments on the homologous series of compounds 5 and 6 have shown19 that as the terminal chains become very long, the
provides a general solution for any situation that requires high twist. In fact experiments on the homologous series of compounds 5 and 6 have shown19 that as the terminal chains become very long, the 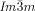 is again replaced by the
is again replaced by the 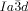 . It would thus appear that such molecules require a twist exceeding the range covered by the
. It would thus appear that such molecules require a twist exceeding the range covered by the 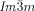 structure. In fact, one can speculate that for an intermolecular twist above 40° the exact match between the helical pitch and segment length ceases to dominate the choice of the phase, and the simpler
structure. In fact, one can speculate that for an intermolecular twist above 40° the exact match between the helical pitch and segment length ceases to dominate the choice of the phase, and the simpler 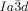 wins once again. Furthermore, due to lateral thermal expansion of the terminal chains, the twist is expected to increase on heating. This would explain the different temperature sequences observed for some homologues, where for the short chain compound an
wins once again. Furthermore, due to lateral thermal expansion of the terminal chains, the twist is expected to increase on heating. This would explain the different temperature sequences observed for some homologues, where for the short chain compound an 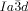 -
-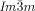 sequence is observed on heating, whereas for the long homologues this sequence is reversed (series of compounds 6).19
sequence is observed on heating, whereas for the long homologues this sequence is reversed (series of compounds 6).19
A closer look at the IsoLT[*]-Cub transitions indicates that the germs of the achiral 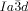 phase emerge always at the interface between the domains with opposite handedness. This appears to be favorable for the formation of this superstructure composed of two enantiomorphic networks (see Figure 2 e and Video 1b). In contrast, the germs of the
phase emerge always at the interface between the domains with opposite handedness. This appears to be favorable for the formation of this superstructure composed of two enantiomorphic networks (see Figure 2 e and Video 1b). In contrast, the germs of the 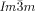 phase are not bound to the domain boundaries. The chiral sense of the nuclei once formed is retained and growth takes place preferentially within the same domain. But there is also a slower growth into domains with opposite chirality, leading to a change of the relative areas of the different domains (compare Figure 2 c,d, see also Video 1e). This means, that the growing Cub[*]/
phase are not bound to the domain boundaries. The chiral sense of the nuclei once formed is retained and growth takes place preferentially within the same domain. But there is also a slower growth into domains with opposite chirality, leading to a change of the relative areas of the different domains (compare Figure 2 c,d, see also Video 1e). This means, that the growing Cub[*]/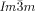 flips over the chirality of the liquid domains if required, although this causes a notable growth retardation.
flips over the chirality of the liquid domains if required, although this causes a notable growth retardation.
In summary, we have discovered that, in spite of appearing in achiral compounds, the 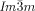 cubic LC phase is chiral in all compounds studied, while the
cubic LC phase is chiral in all compounds studied, while the 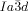 phase is invariably achiral.30 This previously unrecognized features have led us to propose a model of the two phases based on networks with helical segments where the twist sense propagates in 3D across macroscopic domains through matching twist at network junctions. While the opposing chiralities of the two networks of the
phase is invariably achiral.30 This previously unrecognized features have led us to propose a model of the two phases based on networks with helical segments where the twist sense propagates in 3D across macroscopic domains through matching twist at network junctions. While the opposing chiralities of the two networks of the 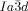 phase cancel, this cannot happen in the triple network
phase cancel, this cannot happen in the triple network 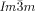 phase. This model also offers, for the first time, a feasible explanation for the existence of the complex
phase. This model also offers, for the first time, a feasible explanation for the existence of the complex 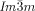 phase, and for the observed
phase, and for the observed 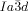 –
–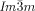 phase sequences as a function of chain length and temperature. The structural insight acquired herein promises to end one of the longest persisting mysteries in the liquid crystal field, that started with the discovery of the “smectic-D” phase over half a century ago.31, 32 But the importance of this finding goes far beyond the systems discussed herein and contributes to the general understanding of symmetry breaking in soft condensed matter.
phase sequences as a function of chain length and temperature. The structural insight acquired herein promises to end one of the longest persisting mysteries in the liquid crystal field, that started with the discovery of the “smectic-D” phase over half a century ago.31, 32 But the importance of this finding goes far beyond the systems discussed herein and contributes to the general understanding of symmetry breaking in soft condensed matter.