The Inverted Bond in [1.1.1]Propellane is a Charge-Shift Bond†
The research in Xiamen is supported by the Natural Science Foundation of China (No 20533020, 20873106) and the National Basic Research Program of China (204CB719902). S.S. is supported by an ISF grant (16/06)
Graphical Abstract
Bonded or not bonded? An ab initio valence bond study of [1.1.1]propellane shows that the two bridgehead carbons are linked by a strong and direct σ bond that is neither classically covalent nor classically ionic, but rather a charge-shift bond, in which the covalent–ionic resonance energy plays the major role. As such, the central bond of [1.1.1]propellane closely resembles the single bond of difluorine.
Abstract
Bonded or not bonded? An ab initio valence bond study of [1.1.1]propellane shows that the two bridgehead carbons are linked by a strong and direct σ bond that is neither classically covalent nor classically ionic, but rather a charge-shift bond, in which the covalent–ionic resonance energy plays the major role. As such, the central bond of [1.1.1]propellane closely resembles the single bond of difluorine.
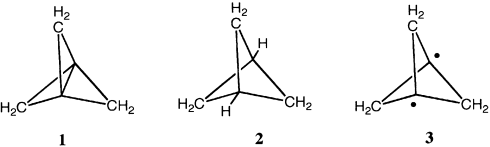
The most intriguing feature of the family of small-ring propellanes is the nature of the central bond that connects the two inverted bridgehead carbons. The properties of the smallest member of the family, [1.1.1]propellane 1, 1
To answer this question, we recall that a positive Laplacian at a BCP is the signature of “charge-shift (CS) bonding”;12 a non-classical type of bonding in which the covalent–ionic resonance energy plays the major role.13, 14 As such, another typical characteristic of CS bonds is the depleted electronic density in the middle of the bond.14 These two CS bond properties are reminiscent of the aforementioned electron density features of the bridge bond of 1.7, 10 Another piece of this puzzle is the recent analysis of the electron localization function (ELF) of various propellanes by Polo et al.,15 which showed strong similarities between the bridge bond of 1 and the single bond of F2, a typical CS bond.16 Thus, CS bonding might be the key feature that reconciles all of the seemingly contradictory data on the central bond of [1.1.1]propellane. Incidentally, Polo et al. interpreted their results in terms of an almost completely ionic bridge bond,15 which would be unprecedented for a homonuclear bond. This intriguing conjecture of a completely ionic CC bond, and Luger's recent data,11 prompted us to characterize the nature of the “inverted bond” in [1.1.1]propellane. To obtain unequivocal insight on the nature of this enigmatic bond, we employed modern ab initio valence bond (VB) methods, which provide all the requisite key properties, such as the weights of the covalent and ionic components of the bond, the covalent–ionic resonance energy, the shape of the covalent dissociation curve.
To investigate the inverted bond, we optimized the geometry of 1 using the MP2 and CASPT2 methods, and performed subsequent VB calculations on these geometries (see the Methods Section). Indeed, the singlet state 1 of [1.1.1]propellane (Figure 1) has a single minimum with a short central bond of 1.596 Å (CASPT2/6-31G*), in good agreement with earlier calculations and with experiment. The triplet minimum 3 lies 98.1 kcal mol−1 higher, in general agreement with the previously reported high value, calculated at a lower level.5 At the singlet optimum geometry, the vertical singlet–triplet energy gaps amounts to 109.1 kcal mol−1, which is a sufficiently large value to rule out a putative diradical nature of the ground state.

Energies E (in hartree) of the singlet (bottom curves) and triplet states (top curves) of [1.1.1]propellane as a function of the bridge bond distance calculated at the MP2/6-31G* and CASPT2/6-31G* levels. Singlet state: ▪ MP2, • CASPT2; triplet state: ▴ MP2, ▾ CASPT2.
The hybrid atomic orbitals (HAOs) located at the bridgehead of 1 are outwardly directed, which is in agreement with the general consensus that there is a degree of hybridization lying in between the classical sp and sp2 hybrid orbitals, or more precisely, sp1.57. Does the stability of 1 then arise from a direct σ bond between these two HAOs or, as has also been suggested, from bonding multicenter orbitals involving both the pair of bridgehead carbons and the methylene wing groups?3 VB theory can settle the question, since it enables one to calculate the bonding strength in situ by focusing on the central bond by itself.
In VB theory and in the chemist's language, a bond is regarded as an interaction between two localized HAOs. In the homonuclear case, this interaction always takes the form of a combination of a major covalent structure and two minor ionic ones (Scheme 1). Note that the covalent structure is itself a combination of two neutral components that differ from each other by an exchange of spins.14 It is this exchange that causes bonding in the covalent structure. On the other hand, any one of these neutral components defines, by itself, a so-called “quasiclassical (QC) state” that is nonbonding and can serve as reference for gauging the bond strength.
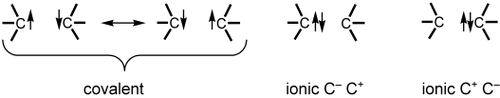
The three VB structures that completely describe a CC bond.
Using the QC state as a nonbonded reference, the energy difference between the QC state and the ground state is a direct measure of the stabilization associated to the exchange of the two electrons in the covalent VB structure, and is complemented by the resonance energy stabilization owing to the mixing of the ionic structures into the covalent structure (Scheme 1). This energy difference measures the in situ bonding energy, which is a vertical quantity and is generally larger than the thermochemical bond dissociation energy (BDE). This is because as one brings together two fragments from infinity to a bonding distance, the bonding interaction is weakened by the repulsions between the adjacent bonds or lone pairs of the fragments facing each other. This repulsion is accounted in the BDE quantity but not in the in situ bond strength. However, the latter gives a reliable measure of the bonding interaction strength. For example, in ethane, the in situ bonding energy is 138.5 kcal mol−1, and the BDE is 96.1 kcal mol−1, as calculated at the breathing orbital valence bond (BOVB) level (Table 1). In [1.1.1]propellane, the in situ bonding energy of the central CC linkage is 119.1 kcal mol−1, which is only 19.4 kcal mol−1 less than in ethane, thus clearly indicating a significant σ-bonding direct interaction between the bridgehead HAOs.
|
Ground state |
QC state[a] |
Covalent–ionic resonance energy[b] |
BDE[c] |
|
|---|---|---|---|---|
|
ethane |
0 |
138.5 |
36.3 |
96.1 |
|
propellane 1 |
0 |
119.1 |
72.2 |
– |
- [a] The difference between the energy of the QC state and that of the ground state gives the “in situ” bonding energy. [b] REc-i is calculated relative to the covalent-only structure. [c] Bond dissociation energy as calculated in the traditional way as the difference between the energy of the molecule and that of the separate fragments.
Having established the strength of the central bond in 1, the next question is what the nature of this bond is: classically covalent, ionic, or charge-shift? Knowledge of two quantities will settle this assignment: The first is the ratio of the respective weights of ionic versus covalent structures. The second is the resonance energy arising from the mixing of covalent and ionic structures (REc-i), defined as the energy difference between the ground-state and the major VB structure. The covalent and ionic weights in the central bond of 1 are quite comparable to those of the CC bond in ethane (Table 2). In both cases, the covalent structure contributes ca. 60 % of the wave function of the ground state, whereas the ionic structures have smaller weights. As was shown before,13, 14 such a predominance of the covalent structure may characterize covalent and CS bonds, but certainly not ionic bonds. Thus, the present VB calculations do not support the statement of Polo et al. that the central bond of [1.1.1] propellane is predominantly ionic.15
|
Covalent |
Ionic C−C+ |
Ionic C+C− |
|
|---|---|---|---|
|
ethane[a] |
55 % |
23 % |
23 % |
|
propellane[b] |
62 % |
19 % |
19 % |
- [a] Ref. 14. [b] This work.
As the covalent structure is definitely established as the major contributor in both ethane and propellane, the resonance energy REc-i will simply be the energy difference between the covalent structure and the ground state (Table 1, column 3). By definition, a bond is considered to be of the charge-shift type if REc-i contributes more than 50 % to the overall bonding energy.14 Table 1 shows that ethane, with an REc-i of only 36.3 kcal mol−1 (BDE=96.1 kcal mol−1), is a classical covalent bond. In contrast, the REc-i of the central bond of propellane is exceptionally large (72.2 kcal mol−1), which is to our knowledge the largest REc-i ever calculated for a homonuclear bond. By comparison, the REc-i value of F2, the most typical CS bond to date, is 5.5 kcal mol−1 smaller.14 REc-i can also be compared to the BDE of the bridge bond that we estimated from considerations of in situ bonding energies, to be about 20 kcal mol−1 smaller than that of the CC bond of ethane; that is, about 70 kcal mol−1. By any measure, this estimation shows that REc-i contributes more than 50 % to the bond strength of the bridge bond of 1, thus definitely putting this bond in the CS-bonding category.14
Another general feature of CS bonding in homonuclear bonds is the shape of the covalent dissociation curve, which, in contrast with a deep covalent potential well in the case of a classical covalent bond, is only weakly bonding or even repulsive.14 Schematic energy profiles of the ground state, covalent VB structure, and QC state for ethane and propellane as a function of the CC distance are given in Figure 2. It is seen that the covalent structure of ethane has, as expected, an attractive profile that is close to the ground-state profile and accounts for most of the bonding energy, whereas the covalent structure of the bridge bond of [1.1.1]propellane is repulsive and rises in energy from 1.6 Å to 1.8 Å, in close analogy with difluorine.13d, 14
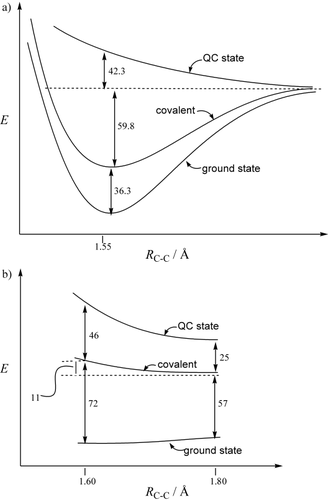
Energy profiles of the ground state, covalent VB structure, and quasi classical state as a function of the CC distance for a) ethane and b) [1.1.1]propellane, and calculated at the BOVB level. Energies are given in kcal mol−1.
The nature of a two-electron bond can also be deduced from considerations of electron densities. As we have shown in a VB study of a series of two-electron bonds,12 a classically covalent bond has a large-density ρ and a negative Laplacian ∇2ρ at BCP, whereas homonuclear CS bonds have large densities and positive or zero Laplacians. In their experimental study of a [1.1.1]propellane derivative, Luger et al. reported values for ρ and ∇2ρ at BCP for the wing bonds and for the central bond.11 They obtained values of ρ=1.55 and ∇2ρ=−13.0, and ρ=1.31 and ∇2ρ=10.3 for the central bond. Clearly, according to our recent study,12 these results classify the wing bonds as classically covalent and the central bond as a CS bond. Another indication that arises from ELF analyses of the CS character of a bond is the absence of a disynaptic basin in the middle of the bond and the presence of two separate monosynaptic basins, as was found in F2 and Cl2.14 Precisely this observation was made by Polo et al., who found an extremely low disynaptic basin population (0.13) between bridgehead carbon atoms of 1, and two monosynaptic basins (population 1.27 each) on these atoms outside the [1.1.1]propellane cage.15
In summary, we have shown herein that the bridgehead carbons of [1.1.1]propellane are linked by a direct two-electron σ bond having significant strength that is very close to the CC bond in ethane, but being very different in its nature. This homonuclear bond is neither classically covalent nor classically ionic, but is rather distinctly a CS bond, and is very similar to the FF bond. All the criteria that may be used to probe the nature of a two-electron bond (covalent–ionic resonance energy, repulsive covalent curve, density and its Laplacian at the BCP, and ELF studies) converge to this very same conclusion. This description resolves the longstanding question of more than two decades. Based on the repulsive nature of the covalent curve, it can be predicted that analogues of [1.1.1]propellane, in which the CH2 groups at the wings are replaced by powerful electron donors, such as NH, O, and S, if they can be synthesized, will have a greater CS character and even shorter “inverted” CC bonds.17 The present analysis of [1.1.1]propellane and the future testing of the prediction about its heteroatomic analogues17 will further demonstrate that CS bonding constitutes a unique and significant class of bonding.
Methods Section
 ((1))
((1))