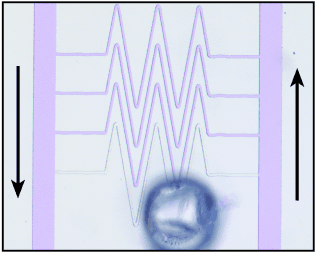
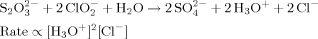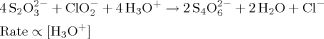Minimal Functional Model of Hemostasis in a Biomimetic Microfluidic System†
This work was supported by NSF CAREER Award, Office of Naval Research Young Investigator Award (N00014-03-10482), Searle Scholars Program, and by Dreyfus New Faculty Award. We thank Professors G. M. Whitesides, C. Chen, C. Hall, T. Van Ha, V. Turitto, and M. LaBarbera for invaluable suggestions.
Graphical Abstract
The proof of the model is in the function: A minimal model of hemostasis (a complex biochemical network responsible for blood coagulation) may be implemented with only three chemical reactions, which creates a biomimetic functional microfluidic system that is capable of repairing itself (as modeled in the figure). This simple system shows threshold response and sensitivity to flow similar to that observed in hemostasis.
Biology is functional, and this function both inspires and puzzles. Inspiration from biology has led to the development of biomimetic systems—artificial systems that function by mimicking biology. Biomimetic systems have been successfully created in self-assembly,1, 2 materials,3 chemical synthesis,4 and surface chemistry.5 They often provide insight into the puzzles of biology, because to develop a biomimetic system, models of biology must be created and tested. In this paper we show how this approach can be extended to a dynamic, nonequilibrium chemical system. We describe a minimal model of hemostasis, then show how this model may be implemented with chemical reactions and used to create a functional microfluidic system that is capable of repairing itself by mimicking hemostasis.
Hemostasis is a complex functional system that consists of approximately 80 coupled biochemical reactions that involve both soluble proteins and platelets. It is responsible for repairing damaged blood vessels and preventing excessive bleeding. It maintains blood in a fluid, clot-free state under normal conditions, but creates a localized solid clot in response to vascular damage.6 The complexity of hemostasis is associated with a finely tuned self-regulation, essential for its function. This self-regulation is believed to be the basis of two essential features of healthy hemostasis: 1) Hemostasis shows a threshold response. There is no response to small regions of internal vascular damage present throughout the circulatory system, but full response to substantial damage of a blood vessel; 2) hemostasis acts locally. A clot formed in the region of substantial damage is confined to that region. These two features are responsible for preventing excessive clotting that obstructs the blood flow and is associated with life-threatening conditions such as deep-vein thrombosis.
Self-regulation in hemostasis is thought to be the direct result of a delicate balance between the initiation and inhibition modules; the flow of blood is essential to achieving this balance.7–9 The network of interacting reactions in hemostasis is difficult to model;10 this difficulty is inherent to complex reaction networks.11, 12 The interactions between reactions and the role of fluid flow are difficult to model by considering isolated reactions of hemostasis. The system has to be modeled as a whole.11, 13, 14 It is challenging to model hemostasis by explicitly treating fluid flow and each of approximately 80 reactions. Although such modeling gives valuable insights into the dynamics of hemostasis,7 it would be difficult to use it as a basis of a biomimetic system. Therefore, simplifications are needed.
We simplified this complex system while still treating it as a whole using a modular approach.15–18 We separated the system into three interacting modules (initiation, inhibition, and precipitation), and represented each module by a single reaction with appropriate kinetics (Figure 1). These modules are coupled—the initiation module is responsible for inducing the formation of the precipitate, and the inhibition module is responsible for preventing formation of precipitate and for dissolving precipitate that is already formed (in analogy to fibrinolysis). Threshold response is provided by the interactions of the inhibition and initiation modules, as was previously proposed.19, 20 The modules interact via a single control molecule C with concentration denoted [C]. We modeled the initiation module with an autocatalytic reaction that produces C with a rate proportional to [C]α (α>1, green curve in Figure 1), modeled the inhibition module with a reaction that consumes C with a rate linearly proportional to [C] (blue line in Figure 1), and modeled the precipitation module with an equilibrium reaction that produces a precipitate at high concentrations of C (orange line in Figure 1). This model is minimal because removal of any of the three reactions should disrupt the function.
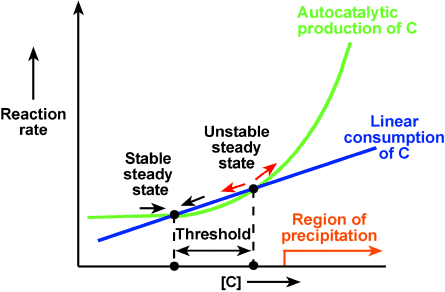
Graphical representation of the minimal kinetic model of self-regulation in hemostasis. The threshold response of hemostasis is modeled to arise from the existence of two steady states that correspond to the crossing points of the two reaction curves describing competing production and consumption of a control molecule C. The left steady state is stable. A small perturbation that decreases [C] from this steady state moves the system to the left, where the rate of production of C is higher than the rate of consumption, causing [C] to increase until the system returns to the steady state (black arrow). A small perturbation that increases [C] from this steady state moves the system to the right, where the rate of consumption exceeds the rate of production, causing [C] to decrease until the system returns to the steady state (black arrow). The right steady state is unstable by the same analysis (red arrows). An increase of [C] larger than the threshold (from the stable to the unstable steady state) triggers production of large amounts of C and causes precipitation.
Hemostasis is a dynamic nonequilibrium system, therefore it was analyzed in terms of reaction rates and steady states, rather than equilibria (Figure 1). We modeled the threshold response observed in hemostasis21 by a system with two steady states: one stable (left in Figure 1) and one unstable (right in Figure 1). Threshold response is common in systems with multiple stable and unstable steady states, and is the basis of excitability.22 In our model, these steady states arise naturally from the kinetics of the initiation and inhibition modules; they correspond to the crossing points of the two curves (Figure 1), where the rate of production of C equals the rate of consumption of C. Multiple stable and unstable steady states have been proposed to exist in hemostasis and were used successfully to explain the effect of mass transfer on the rate of production of thrombin.23 The stability of steady states is established using linear stability analysis22 or graphically (Figure 1).
According to this minimal model, hemostasis is normally in the stable steady state. The threshold equals the difference between [C] at the unstable and stable steady states. Perturbations in [C] decay if they are smaller than the threshold. The system returns to the steady state after these perturbations. Perturbations in [C] grow if they are larger than the threshold. They increase [C] past the unstable (right) steady state, and lead to rapid production of C until the reagents are exhausted (this third steady state is not shown in Figure 1). The rapid production of [C] causes precipitation by the reaction of the precipitation module.
We created a biomimetic system by implementing this model using three chemical reactions that have hydronium (H3O+) ions as the control species C. The initiation and inhibition modules were constructed using the two competing chlorite-thiosulfate reactions well characterized by Epstein.22, 24–26
Reaction 1 produces H3O+ ions and is second-order autocatalytic with respect to [H3O+]. Reaction 2 consumes H3O+ ions and its rate is linearly proportional to [H3O+]. We used these reactions in the range of concentrations where they exhibit sensitivity to stirring and flow.24 To allow for precipitation, we added a third reaction (Reaction 3) between H3O+ ions and a water-soluble sodium alginate. This reaction produces a gel of alginic acid at a high concentration of H3O+, when Reaction 1 becomes dominant.
The proof of the model is in the function. We used microfluidic systems to test if the model reactions could mimic hemostasis and to develop a functional microfluidic system with the ability to repair itself. The utility of this approach has been demonstrated by a self-repairing biomimetic system created to mimic the ability of vertebrae to reorganize after a deformation.1 To create the biomimetic model of hemostasis, we designed networks of microfluidic channels to test whether the model reproduces two essential features of healthy hemostasis—both threshold and local response under conditions of flow.
Absence of blood flow is known to be detrimental for hemostasis, and it is a part of a classic Virchow's triad of factors that cause thrombosis, which can be described as excessive clotting that propagates into vessels that are not damaged.6 Initiation of clotting through the extrinsic pathway is believed to occur when a patch of the subendothelial layer of a blood vessel is exposed by damage. In the absence of flow, autocatalysts produced by the damage activate soluble autocatalysts in the plasma.27 Clotting initiated by the damaged patch propagates throughout the vessel,28 leading to thrombosis.
We observed this phenomenon experimentally in our model system when the reaction mixture containing all of the components was placed into a microfluidic channel in the absence of flow. Initiation of the reaction in one region of the microfluidic channel led to propagation of the acidic chemical front22 throughout the channel with a velocity (Vf) of 3.6 mm s−1 (Figure 2 a). Formation of the gel of alginic acid in the acidic regions (yellow) is analogous to clot formation. The velocity Vf [m s−1] of this planar chemical front (Figure 2 a) can be estimated from the diffusion coefficient of the autocatalyst DC [m2 s−1], and the normalized rate of the reaction Vr [s−1]: Vf≈(Vr DC)1/2. Once the reaction is initiated on a patch inside the microfluidic channel, the autocatalyst C is produced and diffuses out to increase [C] above the threshold concentration in the adjacent regions, which initiates the reaction and causes propagation of the front. If the patch is too small, the loss of the autocatalyst by diffusion from the patch is more rapid than the initiation of the reaction, and the front does not propagate because the concentration of the autocatalyst does not exceed the threshold. In the absence of flow the critical size of the patch pc [m] can be estimated from the critical curvature in the eikonal equation, by comparing the rates of diffusion and reaction: pc≈(DC/Vr)1/2, or by expressing it as a function of the front velocity pc≈DC/Vf.29
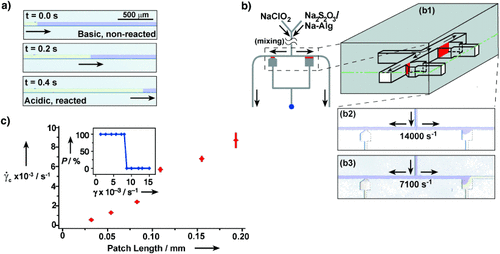
Chemical implementation of the minimal model. a) Behavior analogous to thrombosis in the absence of flow: Time-lapse images of propagation (3.6 mm s−1) of the acidic chemical front, followed by gelling of alginic acid (clot), through a 50×50 μm2 microfluidic channel; b) images showing the threshold response of the minimal model of hemostasis: (b1) is a schematic drawing of splitting region. The gray box represents PDMS, in which the channels were fabricated. Solutions were allowed to mix prior to reaching the region shown. In the absence of external stimuli the reaction mixture remained basic and clot-free (purple). (b2) is a microphotograph of the splitting region (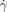 =14 000 s−1) after external initiation at the central outlet (blue dot). Clot propagation into the flowing regions was not seen at either the large (185-μm long) or small (60-μm long) acidic patches; the patches refer to the interfaces (red) between the acidic gel and the flowing basic solutions shown in the schematic drawings. (b3) is a microphotograph of the splitting region (
=14 000 s−1) after external initiation at the central outlet (blue dot). Clot propagation into the flowing regions was not seen at either the large (185-μm long) or small (60-μm long) acidic patches; the patches refer to the interfaces (red) between the acidic gel and the flowing basic solutions shown in the schematic drawings. (b3) is a microphotograph of the splitting region (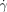 =7100 s−1) after external initiation at the central outlet. Clot propagation into the flowing region was seen only at the large acidic patch; c) plot of critical shear rate (
=7100 s−1) after external initiation at the central outlet. Clot propagation into the flowing region was seen only at the large acidic patch; c) plot of critical shear rate (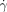 c) as a function of patch length. The inset shows a graph of probability of initiation (P) versus the shear rate, illustrating the typical threshold response observed. The 185 μm patch was used as an example. The purple solution was generated by mixing equal volumes of two aqueous solutions: 1) Na2S2O3 (0.1 M, pH 9.3), the sodium salt of alginic acid (Na-Alg, 0.03 M), and bromophenol blue (0.001 M), and 2) NaClO2 (0.03 M, pH 10.8). We used a pH indicator, bromophenol blue, to follow the propagation by a visible color change from purple (basic) to yellow (acidic). In all cases the depth of channels was 50 μm.
c) as a function of patch length. The inset shows a graph of probability of initiation (P) versus the shear rate, illustrating the typical threshold response observed. The 185 μm patch was used as an example. The purple solution was generated by mixing equal volumes of two aqueous solutions: 1) Na2S2O3 (0.1 M, pH 9.3), the sodium salt of alginic acid (Na-Alg, 0.03 M), and bromophenol blue (0.001 M), and 2) NaClO2 (0.03 M, pH 10.8). We used a pH indicator, bromophenol blue, to follow the propagation by a visible color change from purple (basic) to yellow (acidic). In all cases the depth of channels was 50 μm.
Fluid flow over the patch should increase pc by removing the autocatalyst, and this effect has been predicted for hemostasis.8 Initiation of clotting in hemostasis is predicted to show a threshold response with respect to both the size of the patch and shear rate of the flow.8 It is believed that under normal physiological conditions there are multiple small patches of damaged surface on vessels,7 but in the presence of flow these patches do not initiate clotting.
To test the threshold behavior of the model system in the presence of small acidic patches inside the channels, we designed a microfluidic device in which patches analogous to damaged surfaces can be easily introduced (Figure 2 b). The reagents were allowed to continuously flow in through the two inlets and out though all three outlets. The solutions were allowed to mix completely before they reached the splitting region ((b1) in Figure 2 b). Then the central outlet was blocked to stop the flow and initiate clotting in this channel. The clot propagated (similar to Figure 2 a) into both dead volume regions, producing two patches ((b2) and (b3) in Figure 2 b) of different sizes that presented H3O+-filled gel to the flowing solutions.
At shear rates (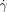 ) above 8000 s−1 neither of the patches induced clotting in the flowing reaction mixture ((b2) in Figure 2 b), but below the critical shear rate (
) above 8000 s−1 neither of the patches induced clotting in the flowing reaction mixture ((b2) in Figure 2 b), but below the critical shear rate (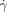 c) of 8000 s−1, only the larger patch initiated clot formation in the flowing reaction mixture (b3; see inset in Figure 2 c). We measured
c) of 8000 s−1, only the larger patch initiated clot formation in the flowing reaction mixture (b3; see inset in Figure 2 c). We measured 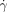 c for patches ranging from 25–185 μm, and confirmed that the critical shear rate increases for larger patches. We confirmed that for sufficiently small patches the reaction did not initiate even in the absence of flow. We could not fabricate devices with sufficiently small patches for the reaction mixture with Vf=3.6 mm s−1 studied in Figure 2 c. We decreased the front velocity to Vf=0.96 mm s−1 by increasing the initial pH value of the reaction mixture and slowing the reaction. For this mixture in the absence of flow the reaction did not initiate for patches below pc≈9 μm, in surprisingly good agreement with the simple estimate of pc≈DH+/Vf≈11 μm, where DH+≈10−8 m2 s−1.
c for patches ranging from 25–185 μm, and confirmed that the critical shear rate increases for larger patches. We confirmed that for sufficiently small patches the reaction did not initiate even in the absence of flow. We could not fabricate devices with sufficiently small patches for the reaction mixture with Vf=3.6 mm s−1 studied in Figure 2 c. We decreased the front velocity to Vf=0.96 mm s−1 by increasing the initial pH value of the reaction mixture and slowing the reaction. For this mixture in the absence of flow the reaction did not initiate for patches below pc≈9 μm, in surprisingly good agreement with the simple estimate of pc≈DH+/Vf≈11 μm, where DH+≈10−8 m2 s−1.
We tested whether our model could mimic the ultimate function of hemostasis: the ability to self-repair by localized clotting. To demonstrate this phenomenon we used a microfluidic device with a large (250 μm in width) inlet channel (“artery”) and a large outlet channel (“vein”) connected by a bed of 25 μm capillaries (Figure 3). This device was designed biomimetically so that the capillaries connected directly to a vessel with a much larger cross-sectional area, similar to the connections found in the human circulatory system (Figure 3 a).30 We introduced solutions into this device as in the experiment described in Figure 2 b. In the absence of damage the flow was stable and no clotting occurred (Figure 3 a). Puncturing the device with a syringe needle through the polydimethylsiloxane (PDMS) resulted in initial leakage, and formation of a small volume of the reaction mixture exposed to air with minimal fluid flow. In this region the reaction spontaneously initiated and a gel of alginic acid (yellow clot) formed, which blocked the damaged area and stopped the leakage of the solution. Spontaneous initiation of this reaction may be due to fluctuations of concentration,24 but we have not excluded absorption of CO2 from air, or evaporation of the solution as causes of initiation. The clot propagated throughout the damaged capillary, but remained localized within the capillary ((b1) in Figure 3 b) and did not induce clotting in the larger channels, in analogy to the experiment described in (b2) in Figure 2 b. As a control, we punctured such a microfluidic device when the solutions were lacking one of the reagents, sodium chlorite. In this case the damage to the device did not induce clot formation and resulted in continuous, severe leaking through the hole ((b2) in Figure 3 b). We emphasize that this model is minimal and it will not explain all of the nuances of hemostasis. Self-repair in this biomimetic system is similar to the initial repair achieved by the formation of the hemostatic plug in biological systems. It is less sophisticated than complete biological repair, in which tissue eventually re-grows to replace the hemostatic plug.
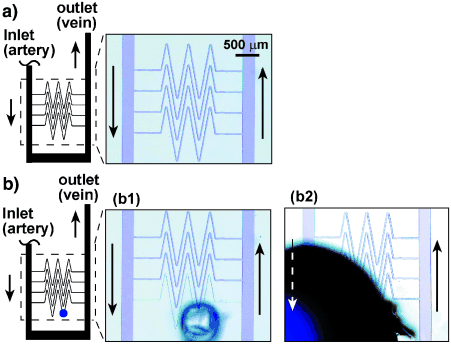
Biomimetically designed self-repairing microfluidic devices: a) Schematic drawing and a microphotograph of a solution prior to initiation in the biomimetic microfluidic device. The black arrows indicate the direction of flow; b) (b1) shows self-repair in the biomimetic device. Use of the complete reaction mixture (Na2S2O3/Na-Alg and NaClO2) resulted in formation of a localized clot and minimal leaking when the capillary bed was punctured (blue dot); (b2) shows when the NaClO2 component of the reaction mixture was removed, puncturing the device in the same location as in (b1), led to severe leaking through the hole. All channels were 50-μm deep. Small channels (capillaries) were 25-μm wide and large channels were 250-μm wide.
This model may be also used for generating new hypotheses describing hemostasis. Traditionally, the evolution of vascular systems has been considered from the point of view of Murray's law, taking into account mass transport, gas exchange, and the hydrodynamic efficiency of pumping.30 These criteria are clearly important for the overall structure and design of a vascular network, but they are more difficult to apply to the local features of the network, such as the geometry of junctions of blood vessels. For example, changes in the geometries of junctions of small vessels will not significantly affect the overall pressure drop for the flow of blood through the vascular system.
Here we propose a hypothesis that some local features may have evolved to accommodate the self-regulation of hemostasis. We designed a non-biomimetic network of channels, where small capillaries were connected to large veins and arteries through triangular expansions (Figure 4), rather than a direct connection,30 as in the biomimetic device (Figure 3 a). After the flow of reagents was established as in Figure 3 a, the capillary was punctured with a syringe needle. The reaction initiated, and the clot stopped the leaking, just as it did in the biomimetic device. Unlike the biomimetic device, the response of this system was not local—when the clot propagated through the damaged capillary it did not stop at the capillary–vein junction, but propagated into both the vein and the artery (Figure 4).
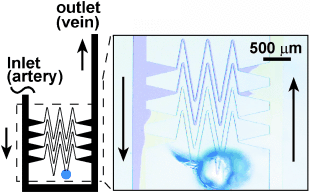
Use of a non-biomimetic capillary design to show the critical role of the ratio of cross-sectional surface areas of the capillaries and larger vessels. Here, the capillaries are joined to the larger vessels through an opening that is 300-μm wide. The device was able to self-repair when punctured, but the clot propagated into the larger vessels (yellow) due to the large acidic patch formed at the interface between the capillaries and the large vessels. All channels were 50-μm deep. Small channels (capillaries) were 25-μm wide and large channels were 250-μm wide. As in Figure 2, solutions of Na2S2O3/Na-Alg and NaClO2 mixed prior to reaching the region of interest.
There are two implications of experiments of this type. First, they may provide clues to the design of artificial vessels (e.g., those used for dialysis or bypass grafts) that do not induce clotting. Second, they may provide alternative perspectives on the evolution of vascular systems, traditionally considered from the points of view of mass transport, gas exchange, and the hydrodynamic efficiency of pumping, and not the ability of hemostasis to act locally.30 This experiment suggests a hypothesis that properly functioning hemostasis may have presented an additional evolutionary constraint on the design of vascular systems in biology. We emphasize that this experiment in itself does not test the hypothesis, only suggests it. We are currently using the microfluidic devices we have designed for the model system (e.g., the device shown in Figure 2 b) to test this hypothesis with blood, and to study the dynamics of hemostasis under controlled-flow conditions.
In this system only three chemical reactions have been sufficient to reproduce the function of the complex biochemical network of hemostasis. It is conceivable that one could add additional reactions to each module of the model system—while maintaining the overall kinetics of each module—to make it resemble hemostasis more closely. If such an incremental transformation is possible, one may speculate that hemostasis could have originated as a minimal system composed of a few reactions (at least three, with at least one reaction for each module). The spontaneous appearance of such a simple system early in evolution is not impossible. How to evolve hemostasis, from a minimal system with rather primitive function into a complex system with much more sophisticated function, is a fascinating question. The evolution of hemostasis is also interesting because it has been considered an “irreducibly complex” system; a system that does not function if any of the components are removed, and therefore a system that could not have evolved by incremental addition of components while maintaining its function.31, 32 One may speculate that such evolution could occur through redundant coexistence. For each of the three reactions in the original minimal system, a set of new reactions would have to evolve with the overall kinetics of the original reaction. The function of the system would not be disrupted during the evolution of the new set of reactions, as long as the original and the new reactions coexist. Once the new set of reactions evolves, the original reaction may be lost, also without the loss of function. Such a mechanism may be used in reverse to reduce the complexity of hemostasis without the loss of function (ultimately reducing it to as few as three reactions). These ideas are certainly speculative, but they may be used to generate testable hypotheses, and to stimulate and guide further investigation in hemostasis and other complex systems.
We conclude that we have succeeded in creating a minimal model of hemostasis that can be implemented with purely non-biochemical reactions in a microfluidic device. The system showed properties similar to those of hemostasis, and allowed us to create a biomimetic microfluidic device that repairs itself. This result complements the previous examples that use nonlinear interactions in chemical33–35 or physical36 systems for self-regulation and self-repair.1 In general, the function of biochemical systems arises from interactions of multiple reactions away from thermodynamic equilibrium. We are especially excited by the opportunities and challenges that such functional biochemical systems present to synthetic chemists. Microfluidics may be used to “synthesize” systems of reactions by controlling interactions among the individual reactions, and maintaining them away from equilibrium. Such synthesis of functional systems of reactions (in addition to the synthesis of molecules and assemblies of molecules) could lead to practically useful developments, such as new types of functional microfluidic devices. Synthetic functional systems of chemical reactions may also help understand the biological systems by which they were inspired. As Richard Feynman put it, “what I cannot create, I do not understand.”37