Winkelaufgelöste Spitzenverstärkte Ramanspektroskopie
Kurzzusammenfassung
Trotz intensiver Forschung an spitzenverstärkter Ramanspektroskopie (TERS) wurde die Winkelverteilung der Raman-Streuung bisher nicht experimentell untersucht. Deshalb wird die Relevanz der Winkelverteilung für das gemessene TERS-Signal selten diskutiert. In dieser Arbeit untersuchen wir die Winkelverteilung des spitzenverstärkten Ramansignals in der Fourier-Ebene. Dafür verwenden wir ein Modellsystem aus flach liegenden Kobalt(II)hexadecaflouro-Phthalocyanin Molekülen (CoPcF16), die auf einem glatten Goldfilm adsorbiert sind. Sowohl Vibrationen in der Molekülebene als auch solche senkrecht zur Ebene können beobachtet werden. Die Ramanmoden senkrecht zur Ebene bei 678 cm−1 und 740 cm−1 haben dabei andere winkelabhängige Intensitätsverteilungen als die Ramanmoden parallel zur Ebene bei 1309 cm−1 und 1373 cm−1. Wir interpretieren das gemessene TERS-Signal unter Berücksichtigung der vibronischen Moden, die mithilfe von Dichtefunktionaltheorie (DFT) berechnet wurden, und der direktionalen Ramanstreuung im Bereich (Lücke) zwischen Spitze und Goldfilm, die mithilfe der „Finite-Difference Time-Domain (FDTD)“ Methode simuliert wurde. Wir nehmen an, dass die TERS-Lücke die Ramanschwingungsmoden unterschiedlich weiterleitet, was zu unterschiedlichen Winkelverteilungen in der resultierenden Intensität der Ramanstreuung führt. Unsere Ergebnisse zeigen, dass die TERS-Detektionsgeometrie für das Verständnis der spektralen Eigenschaften nicht vernachlässigbar ist. Das betrifft beispielsweise die Variation relativer Peakintensitäten bei der Untersuchung molekularer Orientierungen oder die Verfolgung chemischer Reaktionen mithilfe der Ramanspektroskopie.
Einführung
Ramanspektroskopie wird routinemäßig verwendet, um die chemische Struktur organischer Moleküle zu untersuchen. Generell ist die optische Auflösung aufgrund der Beugung limitiert und beträgt bestenfalls ungefähr eine halbe Wellenlänge, was deutlich größer ist als die zu beobachtenden Moleküle. Eine der am häufigsten verwendeten Methoden um diese Limitierung zu überwinden ist die spitzenverstärkte Ramanspektroskopie (TERS), die unabhängig voneinander von Zenobi et al.[1] und Kawata et al.[2] 2000 vorgestellt wurde. Wenn eine scharfe, metallische Spitze nah an die Probenoberfläche gebracht und von einem fokussierten Laserstrahl angeregt wird, verhält sie sich wie eine optische Antenne. Das einfallende optische Feld wird dadurch in der Lücke zwischen Spitze und Probe um einige Größenordnungen verstärkt und gleichzeitig bestimmt die Antenne den Transfer aus dem Nahfeld der Lücke in das Fernfeld.[3, 4] Im Jahr 2013 wurde erstmals sub-Nanometer aufgelöste Einzelmolekül-Ramanbildgebung (STM-TERS, ∼80 K, 1.3 · 10−8 Pa) demonstriert.[5] Dadurch wurde die mögliche räumliche Auflösung mit gleichzeitiger chemischer Identifikation auf ∼5 Å reduziert. 2019 wurden zwei weitere Meilensteine erreicht.[6, 7] Es wurde räumliche Auflösung einzelner chemischer Bindungen demonstriert und kurz darauf wurden räumlich und spektroskopisch aufgelöste Photolumineszenz (PL) Abbildungen einzelner Phthalocyaninmoleküle mit einer optischen Auflösung von ungefähr 8 Å veröffentlicht.[8] Diese Ergebnisse wurden in einem kürzlich erschienenen Review-Artikel zusammenfasst.[9] Die Möglichkeit die chemische Struktur einzelner Moleküle im Å-Bereich aufzulösen ist interessant für Chemie, Physik, Materialwissenschaften und Biologie. Daraus entstand das Bestreben die Mechanismen, die die hohe Auflösung bedingen, sehr detailliert zu untersuchen, wodurch experimentelle Daten besser interpretiert werden können. Zudem kann die Technik für ein breiteres Anwendungsfeld entwickelt und verwendbar werden.
Bisher wurden die Verstärkungsmechanismen in TERS-Studien vor allem hinsichtlich spektraler Intensitäten und Energie untersucht. Dabei ist anzumerken, dass ein quantitatives Verständnis der Nahfeld-Verstärkung basierend auf Intensitätsdaten voraussetzt, dass das winkelabhängige Abstrahlmuster der Probe, die Direktivität der Antenne und die winkelabhängige Sammeleffizienz des verwendeten Mikroskops berücksichtigt werden.[10] Generell wird antennenverstärkte Emission über die Abstrahleffizienz η, die Direktivität D und den Antennen-Gain G beschrieben. Die Direktivität ist definiert als das Verhältnis der Intensität p (θ, ϕ), die pro Winkelelement abgestrahlt wird, und der gesamten emittierten Leistung wobei θ der Winkel zur Antennenebene ist und ϕ der Azimutalwinkel. Ebenso wichtig ist der Gain G (θ, ϕ), welcher definiert ist als das Verhältnis zwischen p (θ, ϕ) und der zugeführten Leistung Pr + Pnr, wobei Pr die radiative Leistung ist und Pnr die ohmschen Verluste der Antenne darstellt. Gain G (θ, ϕ) und Direktivität D(θ, ϕ) stehen über die Abstrahleffizienz η in Verbindung: G .[4] Offensichtlich ist also die Winkelverteilung der Intensität p (θ, ϕ), die von der TERS-Lücke ausgeht, der Schlüssel zum Verständnis der Interaktion des Moleküls mit dem Plasmon der Lücke sowie der Auskopplung des Signals aus der (sub-)Nanometer Antennen-Lücke, da diese letztendlich die gemessenen spektralen Eigenschaften bei TERS-Experimenten bestimmt.
Obwohl theoretisch vorhergesagt wurde, dass die Winkelabhängigkeit der abgestrahlten Intensität sehr empfindlich auf Änderungen in der Konfiguration der Lücke und der Geometrie der Spitze reagiert,[11-13] gibt es in dieser Hinsicht kaum systematische experimentelle Untersuchungen. Das liegt sehr wahrscheinlich daran, dass TERS-Experimente konventionell mit Mikroskop-Aufbauten durchgeführt werden, bei denen nur ein Bruchteil des abgestrahlten Signals von einer Seite in einem Winkel von 60–70 Grad zur optischen Achse eingesammelt wird.[8, 14] Eine weitere häufig verwendete TERS-Konfiguration verwendet eine Objektivlinse, die sich unter der Probe befindet, und von dort die gestreute Strahlung einsammelt. In diesem Fall muss das Signal durch das Substrat hindurch detektiert werden. Dabei muss berücksichtigt werden, dass das Abstrahlmuster durch das dielektrische Substrat verändert wird und eine Reflektion an der Molekül-Substrat Grenzfläche auftritt.[15, 16] Somit ist es sehr herausfordernd einen großen Winkelbereich des intrinsischen TERS-Abstrahlmusters zu beobachten.
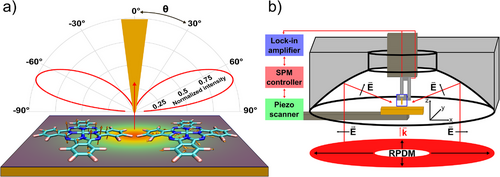
In dieser Arbeit untersuchen wir die Winkelverteilung des TERS-Signals von CoPcF16 Molekülen, die auf einer ultra-glatten Goldoberfläche adsorbiert sind. Das Signal wird von einem Parabolspiegel gesammelt, was in Abbildung 1 verdeutlicht wird. Aufgrund der großen numerischen Apertur (0.9986 in Luft) des Parabolspiegels, der über dem Gold-Substrat platziert wird, kann das Ramansignal, welches aus der Streuung in der Lücke zwischen Spitze und Probe entsteht, systematisch zwischen 27 und 87 Grad um die optische Achse gesammelt werden. Mit dieser Konfiguration ist es möglich die Intensität mit Winkelinformationen in TERS-Experimenten zu korrelieren. Als Testmolekül haben wir fluoriertes Kobalt(II)phthalocyanin gewählt, da es eine hohe photochemische Stabilität und eine starre molekulare Struktur besitzt und homogene Schichten mit flach liegenden Molekülen bilden kann. Filme mit einer solchen molekularen Orientierung wurden für unterschiedliche Übergangsmetall-Phthalocyanin Moleküle, unter anderem CoPcF16, auf einkristallinen metallischen Oberflächen, und für geringe Bedeckungen auch auf vergleichsweise rauen Gold-Substraten, nachgewiesen.[17, 18] Aufgrund dieser Vorteile wurden ähnliche Moleküle für viele wichtige Studien zu submolekularer TERS verwendet.[5-8] Deshalb erscheinen die Ergebnisse unserer Studie zu CoPcF16 sehr relevant für die TERS-Forschung. Um die Winkelverteilung des gestreuten optischen Signals aufzuzeichnen, wurde das Signal aus der hinteren Brennebene unseres Mikroskops analysiert. Um Ramanstreuung von PL-Signal zu unterscheiden, verwenden wir Energie-Impuls TERS, indem wir räumlich Signale aus spezifischen Winkelbereichen selektieren und diese mit einem CCD-Spektrometer analysieren.
Wir haben abstandsabhängige TERS-Verstärkung von flach liegenden CoPcF16 Molekülen auf ultra-glatten Goldoberflächen in den Stokes-, anti-Stokes- und Oberton-Regionen beobachtet. Dies unterscheidet sich vom kürzlich berichteten „TERS quenching“.[19] Wir demonstrieren, dass die TERS-Verstärkung stark genug ist, um das optische Signal aus der Lücke zwischen Spitze und Probe in einzelnen Sektionen der Fourier-Ebene darzustellen und es in diesen Sektionen separat mittels Energie- Impuls-Spektroskopie zu analysieren. Es wurden intensive Ramanspektren aus individuellen Winkelbereichen aufgenommen, welche winkelabhängige Unterschiede in den Intensitäten einzelner Schwingungsmoden zeigen. Wir analysieren diese Unterschiede, indem wir Schwingungsmoden, die in der Molekülebene schwingen, und solche, die außerhalb der Ebene schwingen, unterscheiden. Außerdem wird die gerichtete Streuung durch die Spitze-Probe Konfiguration berücksichtigt. Wir können nachweisen, dass winkelabhängige Ramanstreuung stark vom Plasmon der Lücke und dessen Nahfeld abhängt, während die Direktionalität durch die Form der Spitze, sprich die Antenne, gegeben ist. Unsere Ergebnisse zeigen die große Relevanz der Winkelabhängigkeit beim Verstehen spektraler Merkmale in TERS-Experimenten.
Ergebnisse und Diskussion
TERS von CoPcF16 Molekülen auf einem Goldfilm
Der Einfluss der angeregten plasmonischen Mode der Lücke auf das Raman Signal ist in Abbildung 1a illustriert. Die Winkelverteilung der Raman Dipolstrahlung wird vom lokalen elektrischen Feld in der Nanometer-Lücke auf unterschiedliche Weise beeinflusst. Einerseits kann die gesamte abgestrahlte Leistung durch die Anregung der plasmonischen Mode der Lücke vergrößert werden. Außerdem kann die abgestrahlte Intensität pro Raumwinkelelement p(θ, ϕ) des Raman-Dipols durch das Verhalten der plasmonischen Mode verändert werden. Falls die Frequenz des Ramandipols mit der Resonanzfrequenz einer plasmonischen Mode übereinstimmt, wird das Emissionsmuster der Raman-Streuung durch die plasmonische Mode stark modifiziert.
Um diesen Prozess experimentell zu untersuchen, wird der in Abbildung 1b gezeigte Aufbau verwendet. Eine detaillierte Beschreibung des TERS-Aufbaus kann in SI1 gefunden werden. Eine elektrochemisch geätzte Goldspitze wird mithilfe einer mechanisch angeregten Stimmgabel nah an die Probe gebracht. Der Abstand zwischen Spitze und Probe wird über den Phasenversatz der Oszillation der Stimmgabel kontrolliert, der durch Scherkräfte zwischen Spitze und Probe entsteht. In unserem Experiment wird ein TERS-Lücke aus einer Goldspitze und einer Goldoberfläche erzeugt; ein Phasenversatz von 4.5 Grad entspricht typischerweise einer Lücke von 4 nm („große Lücke“). Vergrößert man den Phasenversatz auf 15 Grad, verkleinert sich die Lücke auf ungefähr 2 nm („kleine Lücke“).[20] Um die plasmonische Mode der Lücke effizient anregen zu können, wird eine radial polarisierte Donutmode (RPDM) mit einer Wellenlänge von 633 nm verwendet. Zum Vergleich wird auch eine azimutal polarisierte Donutmode (APDM) verwendet. Diese weist ausschließlich Feldstärke in der x-y Ebene |Ex,y|2 auf. Detaillierte Information zu den Feldverteilungen von RPDM und APDM sind SI1 zu entnehmen. Ein ungefähr zwei Lagen dicker (0.7 nm) CoPcF16 Film wurde auf eine ultra-glatte Goldprobe aufgedampft (vgl. SI2).
In Abbildung 2 sind experimentell aufgenommene TERS-Spektren zu sehen. Die Verwendung von RPDM (rote Linie) führt zu signifikanter Verstärkung im Vergleich zur Situation ohne Spitze (rote gepunktete Linie). Dies ist auf die starke vertikale plasmonische Mode der Lücke zurückzuführen, die von der dominanten Ez-Komponente im Fokus des RPDM-Strahls angeregt wird. Das TERS-Spektrum, das unter Anregung mit der APDM (blaue Linie) aufgenommen wurde, ist auch dargestellt. Im Vergleich zur Situation ohne Spitze zeigt auch das APDM Spektrum Ramanverstärkung, allerdings nur moderat im Vergleich zum RPDM-TERS. Diese Ergebnisse untermauern die Wichtigkeit der plasmonischen Mode der Lücke für die elektromagnetische (EM) Verstärkung des Ramansignals. Um die individuellen Ramanmoden zu analysieren, haben wir resonante Ramanmoden mithilfe von (zeitabhängiger) Dichtefunktionaltheorie ((TD-)DFT) für CoPcF16 auf Gold unter Berücksichtigung der Adsorptionsgeometrie und der Goldspitze-Goldsubstrat-Konfiguration berechnet (vgl. SI3). Die meisten der prominenten Ramanmoden schwingen in der Ebene, bspw. 967 cm−1, 1194 cm−1, 1307 cm−1, 1335 cm−1, 1373 cm−1, 1474 cm−1, 1540 cm−1. Allerdings gibt es auch zwei Moden, die zu Bewegungen außerhalb der Molekülebene gehören, bei 678 cm−1 und 740 cm−1. Diese können Vibrationen von C- und N-Atomen in der Makrocyclus-Struktur zugeordnet werden (vgl. Abbildung 2b). Die Geometrie der Vibrationen wird später in der Diskussion der winkelaufgelösten Ramanstreuung wichtig.
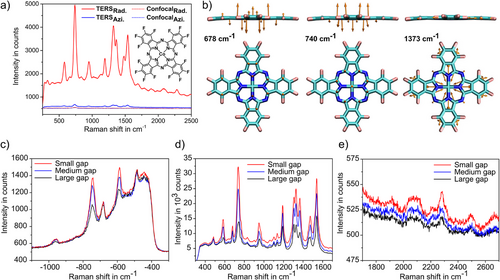
Im Gegensatz zum kürzlich berichteten „TERS quenching“ bei ZnPc Molekülen,[19] beobachten wir große TERS-Verstärkungen. Es gibt einige Faktoren, die beide Experimente unterscheiden und zu den unterschiedlichen Beobachtungen führen könnten. In unserer Studie wurde ein CoPcF16 Film mit einer nominalen Dicke von 0.7 nm verwendet. Im Fall von homogen auf der Goldfläche verteilten Molekülen, entspricht dies zwei Lagen von flach liegenden CoPcF16 im Gegensatz zum Einzelmolekül-Fall in der Studie von Yang et al.[19] Weiterhin sammelt der Parabolspiegel in unserer Studie Signal über einen deutlich größeren Winkelbereich als bei der 60 Grad TERS-Konfiguration. Der Unterschied in den Detektions-Schemata wird in dieser Arbeit detailliert thematisiert. Zudem wurde die von uns verwendete Spitze nicht so modifiziert, dass einzelne Atome am Apex hervorstehen. Zusammen mit dem größeren Abstand zwischen Spitze und Probe im nm-Bereich führt dies zu Unterschieden im EM Nahfeld in der Lücke in unserem Experiment im Vergleich zur oben genannten Arbeit.
Wir beobachten, dass Stokes-, anti-Stokes- und Oberton-Signalstärken mit abnehmendem Abstand zwischen Spitze und Probe zunehmen, was die essenzielle Rolle der EM-Verstärkung in unserer Studie bestätigt (vgl. Abbildung 2c–e). Es sei angemerkt, dass vorangegangene Arbeiten gezeigt haben, dass ein Ladungstransfer zwischen CoPcF16 und Goldsubstrat stattfindet. Dieser Prozess ist bidirektional und involviert das zentrale Metallatom und den Makrocyclus.[18] Deshalb kann der Beitrag der chemischen Verstärkung auf die Ramanintensitäten nicht vernachlässigt werden. Bei genauerer Betrachtung der individuellen Signalverhältnisse ist ein Unterschied in der anti-Stokes Region verglichen mit den Stokes-Linien erkennbar. Beispielsweise ist das Verhältnis während ist. Wir gehen davon aus, dass die selektive Ramanverstärkung der einzelnen Moden, bspw. der anti-Stokes Mode bei −678 cm−1, von der Nähe zur Resonanzfrequenz der plasmonischen Mode der Lücke kommt. Vorherige Studien zu oberflächenverstärkter Ramanspektroskopie (SERS) haben gezeigt, dass die Moden, die näher an der Plasmonenresonanz liegen, selektiv verstärkt werden.[21] Deshalb leiten wir die Plasmonenresonanz der Lücke indirekt aus dem spektralen Hintergrund unseres TERS-Spektrums ab. Der breite „Kontinuum“ TERS (und SERS) Hintergrund ist eng mit der metallischen PL verbunden und wird[22-24] von der Plasmonenresonanz beeinflusst,[20, 25-31] was allerdings immer noch diskutiert wird.[22-24] Wie in Abbildung 2d zu erkennen ist, ist für kleine Lücken das Maximum des spektralen Hintergrunds bei 1.890 ± 0.005 eV zu finden, für größere Lücken verschiebt es sich zu 1.905 ± 0.007 eV ins Blaue. Dieses Phänomen ist typisch für abstandsabhängige plasmonische Moden (vgl. SI4). In Abbildung 2c ist zu erkennen, dass die −678 cm−1 anti-Stokes Mode näher am Maximum des spektralen Hintergrunds liegt als die Mode bei −740 cm−1 und deshalb mehr von der plasmonischen Mode der Lücke verstärkt wird.
Am unteren Ende des Spektrums ist die anti-Stokes Ramanmode bei −967 cm−1 kaum sichtbar, was den abnehmenden Einfluss der plasmonischen Mode der Lücke verdeutlicht. In anderen Experimenten mit breiterem spektralem Hintergrund als dem in Abbildung 2c können anti-Stokes Moden bis zu −1540 cm−1 beobachtet werden (vgl. Abbildung S6a).
Simulation gerichteter Emission einer TERS-Konfiguration
Wir untersuchen die Winkelverteilung des optischen Signals im Fernfeld mithilfe der „finite-difference time-domain“ (FDTD) Methode (vgl. SI5). Das Simulationsmodell besteht aus einer leicht verkippten Goldspitze über einem Goldfilm, der mit einem 1 nm dicken CoPcF16 Film bedeckt ist. Die Geometrie der Spitze ist definiert durch den Durchmesser des Apex (R), den Öffnungswinkel (β) und den Verkippungswinkel (α) zur optischen Achse (z-Achse), wie in Abbildung 3a dargestellt. In Übereinstimmung mit den experimentellen Bedingungen und der tatsächlichen Geometrie der Spitze (bestimmt mittels Rasterelektronenmikroskopie) wurden α = 3°, β = 18° und R = 70 nm verwendet. Die Plasmonenresonanz einer solchen Spitzen-Proben-Geometrie mit einer Lücke von 2 nm beträgt laut Berechnung 640 nm und verschiebt sich für die Spitze ohne Probe ins Blaue zu 587 nm (Abbildung 3b).
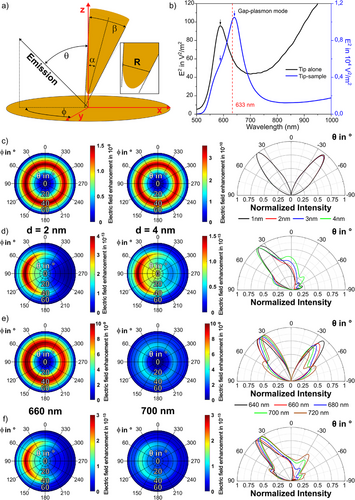
Zuerst haben wir das Fernfeld-Emissionsmuster eines Dipols (vertikal oder parallel zu Probenebene) in der Spitzen-Proben-Konfiguration berechnet. Die Ergebnisse zeigen in beiden Fällen ein deutlich richtungsabhängiges Emissionsmuster. Im Detail zeigt das Fernfeldmuster für den vertikalen Dipol einen gleichmäßigen Ring, der annähernd unabhängig vom Azimutalwinkel (φ) ist, aber stark vom Polarwinkel (θ) abhängt (Abbildung 3c).
Im Gegensatz dazu zeigt der parallele Dipol, geführt durch die leicht verkippte Spitze, ein sichelförmiges Fernfeldmuster, das von sowohl θ als auch φ abhängt. Der parallele Dipol koppelt aufgrund des komplizierten elektromagnetischen Felds in der Nanolücke auch an die plasmonische Mode des Systems, da das lokale elektrische Feld sowohl parallele als auch vertikale Komponenten aufweist, wenn auch mit unterschiedlichen Stärken.[32-34]
Nun analysieren wir die Fernfeldmuster in der x-z-Ebene für unterschiedliche θ-Winkel bei unterschiedlichen Abständen zwischen Spitze und Probe (Abbildung 3c und d). Dabei zeigen sich drei Charakteristika: (1) Der vertikale Dipol zeigt zwei symmetrische Schlaufen bei θ = ±39°. Im Gegensatz dazu konzentriert sich die meiste Strahlung für den parallelen Dipol in einer Hauptschlaufe bei θ = 40° gegenüber der Neigung der Spitze (hier bei φ = 90°). In beiden Fällen hängt der Winkel, an dem die Emission am stärksten ist, nicht vom abnehmenden Abstand zwischen Spitze und Probe von 4 nm auf 2 nm ab. Allerdings vergrößert sich für den parallelen Dipol das Verhältnis für größere Abstände, was eine Abnahme der Direktivität der Antenne indiziert. (2) Die Intensität der Fernfeldemission ändert sich für variierende Abstände schneller für den vertikalen Dipol als für den parallelen Dipol. Das deutet darauf hin, dass der vertikale Dipol mit größerer Kopplungskonstante ge (vgl. SI5) mit der Spitze interagiert als der parallele Dipol. In der Tat ist die Intensität der Fernfeldemission des vertikalen Dipols bei gleichem Abstand um vier Größenordnungen stärker als die Intensität des parallelen Dipols. Dies stimmt mit experimentellen Ergebnissen überein, bei denen hauptsächlich die Vibrationen, die außerhalb der Probenebene schwingen, in TERS-Spektren vorzufinden sind.[35, 36] (3) Das Emissionsmuster des vertikalen Dipols bei d = 2 nm zeigt einen kleineren Divergenzwinkel (∼28°) als das des parallelen Dipols (∼37°). Der Divergenzwinkel ist definiert als die Halbwertsbreite der Schlaufe. Außerdem bleibt der Divergenzwinkel des vertikalen Dipols bei zunehmendem Abstand gleich, während der des parallelen Dipols sich mit zunehmendem Abstand (von 2 nm auf 4 nm) von ∼37° auf ∼59° vergrößert. Deshalb folgern wir, dass die Direktivität der Antenne für den vertikalen Dipol größer ist als für den parallelen Dipol. Weiterhin haben wir die Analyse auf unterschiedliche Emissionswellenlängen erweitert. In Abbildung 3e und f ist ersichtlich, dass die Intensität zunimmt und die Divergenz abnimmt, je näher die Wellenlänge an der Plasmonenresonanz des Systems ist.
Zusammenfassend lässt sich sagen, dass die Simulationen zeigen, dass das Nahfeld in der plasmonischen Lücke zwischen Spitze und Probe das Abstrahlmuster formt und dass die Spitzen-Proben Konfiguration die Strahlung mit hoher Direktionalität ins Fernfeld überführt, allerdings mit signifikanten Unterschieden für parallele und vertikale Dipole im Winkel maximaler Emission, Intensität und Divergenz. Die gemessene Emission ist sowohl von der Distanz zwischen Spitze und Probe als auch von der Wellenlänge abhängig. Diese unterschiedlichen Winkelverteilungen der Fernfeldemission führen zu unterschiedlichen Detektionseffizienzen je nach Orientierung des abstrahlenden Dipols (vgl. SI6). Obwohl der vertikale Dipol stärker mit der Spitze koppelt, ist es möglich, dass seitlich beleuchtete TERS-Konfigurationen bessere Sammeleffizienzen für parallele Dipole aufweisen. Dies ist auf das Emissionsmuster mit nur einer Schlaufe des parallelen Dipols zurückzuführen. Wir betrachten eine Situation, in der mit einer asphärischen Linse mit NA 0.51, die in einem Winkel von 60° zur Oberflächennormalen positioniert ist, Licht von einem parallelen Dipol in der Lücke zwischen Spitze und Probe detektiert wird, während die Spitze leicht verkippt ist (α ≈ 3°). Falls die Linse optimal in der Emissionsschlaufe platziert ist, beträgt die Sammeleffizienz 20.5 %, während sie auf der gegenüberliegenden Seite nur 6.4 % betragen würde (vgl. Abbildung S11). Für einen vertikalen Dipol ist der Unterschied aufgrund des annähernd symmetrischen Abstrahlmusters vergleichsweise gering (maximal 14.9 %, minimal 12.6 %). Deshalb muss bei der Interpretation von TERS-Spektren die Winkelverteilung der Emission zusammen mit der Position der Objektivlinse vor allem beim Vergleich von Vibrationsmoden, die in der Ebene schwingen, mit solchen, die außerhalb der Ebene schwingen, berücksichtigt werden.
Experimentelles winkelaufgelöstes TERS-Signal
Wir haben die Technik zur Bildgebung der hinteren Brennebene[37-39] (Back-focal plane, BFP) am TERS-Aufbau implementiert (vgl. SI7) um das Abstrahlmuster experimentell zugänglich zu machen. In Abbildung 4a ist zu erkennen, wie die abgestrahlte Intensitätsverteilung p (θ, ϕ) eines Dipols in einer TERS-Lücke in die BFP (als rote Scheibe dargestellt) projiziert wird. Das BFP-Muster wird mit den Komponenten des Wellenvektors kx/k0 und ky/k0 skaliert, wobei k0 = 2π/λ. Die Dimension der BFP-Abbildung ist durch die NA des Parabolspiegels bestimmt und beträgt in unserem Fall θmax = 87° und φmax = 360°. Allerdings wird in unserem Experiment aufgrund des Lochs im Parabolspiegel nur der Bereich zwischen θ = 27° und 87° gesammelt. Die Winkelinformationen (θ, φ) des gemessenen Signals werden mithilfe der Parabelgleichung des Parabolspiegels aus der Position auf dem Detektor berechnet. Abbildung 4b zeigt ein experimentell aufgenommenes BFP-Bild, das mit einem TERS-Abstand von 2 nm aufgenommen wurde. Das gemessene Signal ist im Bereich von θ = 35° bis 55° am stärksten (vgl. Abbildung 4c). Der Bereich ohne Signal wird von Probenhalter und einer Zinke der Stimmgabel beschattet (gestrichelt umrandete Fläche).
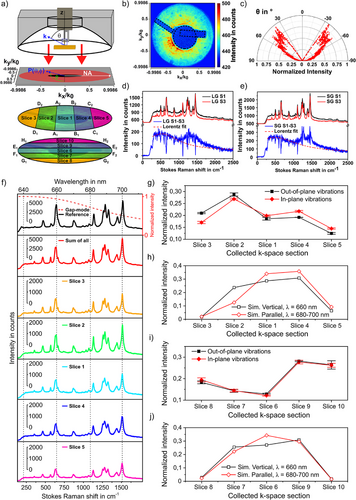
Außerdem haben wir die Energie-Impuls-Spektroskopie Technik[40-43] implementiert, um das winkelverteilte TERS-Signal besser vom breiten PL-Signal unterscheiden zu können. Das erreichen wir, indem wir das optische Signal räumlich in Schnitte („Slices“) gewisser Winkelbereiche (θ, φ) unterteilen, wie in Abbildung 4a gezeigt. Das Signal dieser Schnitte wird dann mit einem CCD-Spektrometer analysiert (vgl. SI7). Die Schnitte 1–5 sind parallel zu ky, während Schnitte 6–10 parallel zu kx sind. Abbildung 4d vergleicht die Energie-Impuls TERS-Spektren von zwei unterschiedlichen Winkelbereichen (Schnitt 1 und Schnitt 3) bei einem Spitzenabstand von 4 nm. Dabei deckt Schnitt 1 alle Punkte zwischen A1 und A2 sowie B1 und B2 ab (vgl. Abbildung 4a). Ebenso beinhaltet Schnitt 3 den Bereich zwischen D1, D2 und dem linken Rand der Apertur. Die genaue Winkelinformation für alle Schnitte ist in der Tabelle S2 zusammengefasst. Nach Subtrahieren der Spektren aus Schnitt 1 und Schnitt 3 zeigen sich in Abbildung 4d deutlich die folgenden Merkmale: (1) Ramanmoden im spektralen Bereich von 473–1129 cm−1 tauchen im Differenzspektrum als Vertiefungen auf, was ihre geringere Intensität im Winkelbereich von Schnitt 1 indiziert. (2) Ramanmoden im spektralen Bereich von 1184–1540 cm−1 zeigen auch negative Intensität im subtrahierten Spektrum. Allerdings ist der PL-Hintergrund hier positiv. Diese Phänomene werden für einen geringeren Abstand von 2 nm in Abbildung 4e stärker und die Intensitätsdifferenzen der Ramanmoden werden in diesem Bereich sogar positiv.
Wir analysieren die Energie-Impuls TERS-Spektren, indem wir die Winkelverteilung aller prominenten Ramanmoden bestimmen und sie mit den simulierten Ergebnissen aus Abbildung 3 vergleichen. Abbildung 4f zeigt eine Serie von TERS-Spektren, die in unterschiedlichen Winkelbereichen aufgezeichnet wurden. Das oberste Spektrum wurde ohne Winkelselektion aufgenommen. Das zweite Spektrum der Reihe ist die Summe aller Spektren der einzelnen Winkelbereiche Schnitt 1–5. Diese Spektren haben vergleichbare Intensitätsverhältnisse der einzelnen Ramanmoden. Allerdings variieren die Intensitätsverhältnisse der einzelnen Ramanmoden in den Spektren, die in unterschiedlichen Winkelbereichen aufgenommen wurden. Um diese Unterschiede zu verdeutlichen, integrieren wir die Intensität einer bestimmten Schwingungsmode für jeden Winkelbereich und normalisieren diese dann auf die Gesamtintensität dieser Mode über alle Winkelbereiche. Nehmen wir als Beispiel die Mode bei 678 cm−1 (Schwingungsmode senkrecht zur Probenebene), so ergibt sich die normalisierte Intensität in Schnitt 1 (S1) zu . Die normalisierte Intensität der anderen Mode senkrecht zur Ebene (740cm−1) ergibt sich analog. Für Abbildung 4g wird dann der Wert für Schnitt x verwendet, um die Winkelverteilung der Ramanmoden vertikal zur Ebene darzustellen. Bei den Schwingungen parallel zur Ebene (967 cm−1, 1309 cm−1, 1331 cm−1, 1373 cm−1, 1469 cm−1 und 1540 cm−1) wird analog vorgegangen, woraus die rote Linie in Abbildung 4g hervorgeht. Die simulierten Fernfeldverteilungen der parallelen (in der Ebene) und vertikalen (außerhalb der Ebene) Dipole werden in die gleichen Schnitte unterteilt und analog normiert, was zu Abbildung 4h führt. Die Schnitte parallel zu kx (S6–S10) ergeben analog die Abbildungen 4i und j.
Zuerst vergleichen wir die Trends bei unterschiedlichen Winkelbereichen der Moden außerhalb der Ebene mit denen in der Ebene. Wir beobachten unterschiedliche Intensitätsverteilungen in den zehn Winkelbereichen für in und außerhalb der Ebene liegende Moden. Beispielsweise ist für Schnitt 2 die normalisierte Intensität der Mode außerhalb der Ebene größer als die der Mode in der Ebene, was jedoch für die Schnitte 1, 4 und 5 umgekehrt ist (Abbildung 4g). Dieses Verhalten deckt sich mit den simulieren Ergebnissen in Abbildung 4h. Es ist wichtig zu erwähnen, dass die durchschnittliche Intensität der Mode außerhalb der Ebene in Schnitt 2 ungefähr 231 % größer ist als in Schnitt 5, was in Abbildung 4g erkennbar ist. Des Weiteren könnengenerell unterschiedliche Winkelverteilungen für Moden in und außerhalb der Ebene erkannt werden. So sind in Schnitt 3 die normierten Intensitäten der Moden senkrecht zur Ebene ungefähr 24 % größer als die der Moden parallel zur Ebene. Für die Schnitte 4 und 5 sind allerdings die normierten Intensitäten der parallelen Moden jeweils 14 % bzw. 17 % größer. Für die Schnitte 6 und 10 sind die normierten Intensitäten der parallelen und senkrechten Moden jeweils sowohl für das Experiment und die Simulation ähnlich. Die in Abbildung 4 gezeigte experimentelle Messung der Winkelverteilung des TERS-Signals wurde in der Abbildung S13 für größere Abstände zwischen Spitze und Probe wiederholt. Dabei hat sich gezeigt, dass der Einfluss des Abstandes auf die Winkelverteilung der Ramanstreuung im Bereich der getesteten Abstände und in Übereinstimmung mit der FDTD-Simulation in Abbildung 3c und d klein ist.
Es sei bemerkt, dass die Trends der Intensitätsverteilungen im Experiment zwar generell gut zu den Ergebnissen der Simulation passen, in manchen Winkelbereichen (Schnitte 1 und 6) allerdings nicht übereinstimmen. Um diese Diskrepanzen zu verstehen, werden folgende Faktoren berücksichtigt: (1) Wie im BFP-Bild (Abbildung 4b) zu sehen ist, wird ein Teil des optischen Signals vom Probenhalter und der Stimmgabel blockiert und/oder gestreut, was das gemessene Signal modifiziert. (2) Es wurde ein CoPcF16 Film und keine einzelnen Moleküle verwendet, weshalb leichte Abweichungen in der molekularen Orientierung gegenüber den in der Simulation angenommenen flach liegenden Molekülen nicht ausgeschlossen werden können. (3) Die tatsächliche Spitzengeometrie ist nur approximiert, da die atomare Struktur des Apex nicht dargestellt werden kann. Bei der Entstehung des TERS-Signals spielen Unebenheiten auf der Oberfläche des Apex eine wichtige Rolle,[44, 45] obwohl deren Stabilität und Effekt bei Umgebungsbedingungen weiterhin unklar ist.[46, 47] In unserer Simulation wurden solche atomaren Merkmale der Spitze nicht berücksichtigt, was weitere Unterschiede zwischen Simulation und Experiment erklären könnte.
Zuletzt wollen wir diese Beobachtungen hinsichtlich der Geometrie der Schwingungsmoden und der wellenlängenabhängigen Direktivität interpretieren. Wie in Abbildung 3e und f gezeigt wurde, ist die Intensität größer und die Divergenz kleiner, je näher die Emissionswellenlänge an der Plasmonenresonanz der Lücke ist. In Abbildung 4d und e liegt das Maximum des spektralen Hintergrundes bei 651 nm bzw. 656 nm, was nah an der simulierten Plasmonenresonanz in Abbildung 3b liegt. Die beiden senkrechten Ramanmoden (678 cm−1 und 740 cm−1) streuen bei ca. 660 nm, was deutlich näher an der Plasmonenresonanz liegt als alle parallelen Ramanmoden (967 cm−1, 1309 cm−1, 1331 cm−1, 1373 cm−1, 1469 cm−1 und 1540 cm−1), die zwischen 680 nm und 700 nm streuen. Dadurch werden die Abstrahlmuster der senkrechten Schwingungsmoden durch die Antenne signifikant gerichtet, was zu stärkerer Fernfeldintensität bei größeren Polarwinkeln wie in Schnitt 3 gegenüber den kleineren Polarwinkeln in Schnitt 1 führt. Deshalb sind diese Moden in den Differenzspektren in Abbildung 4d und e als Vertiefungen zu erkennen. Da die Wellenlänge der gestreuten Photonen im Bereich 680 nm bis 700 nm weniger mit der Plasmonresonanz des Systems überlappen, werden die Moden und deren Abstrahlmuster in diesem Bereich auch weniger stark von der Antenne beeinflusst. In diesem spektralen Bereich ist das winkelabhängige Verhalten der Moden in der Ebene komplexer. Es treten Moden sowohl als Vertiefungen, als auch als Erhebungen im Differenzspektrum auf. Interessanterweise ist die Breite einiger Moden (1309 cm−1, 1331 cm−1, 1373 cm−1 und 1540 cm−1) vergrößert, was zu Erhebungen im Differenzspektrum führt. Um diese Details verstehen zu können sind allerdings weitere Studien notwendig.
Zusammenfassung
Zusammenfassend ergibt sich, dass Energie-Impuls TERS mittels Parabolspiegel sehr deutlich die schwingungsmoden-spezifische Winkelverteilung der Ramanintensität zeigen konnte. Das Abstrahlmuster von parallelen oder vertikalen Dipolen wird stark vom Nahfeld in der Nanolücke zwischen Spitze und Probe beeinflusst und die Emission wird mit großer Direktionalität von der Antenne aus Spitze und Probe ins Fernfeld gerichtet, allerdings mit signifikanten Unterschieden zwischen den Moden beim Winkel der maximalen Intensität, der Intensität und der Winkeldivergenz. Es wurde gezeigt, dass das TERS-Signal stark winkelabhängig ist, was große Variationen in den spektralen Merkmalen von TERS zwischen unterschiedlichen TERS-Aufbauten (Beleuchtung von der Seite/von oben mit einem Parabolspiegel/von unten) oder unterschiedlichen Spitzen induzieren könnte.
Zusatzmaterialien
Die Autoren haben in der SI weitere Referenzen zitiert.[7, 29, 48-78]
Danksagung
Wir bedanken uns bei Philipp Haizmann für die Unterstützung in der Schichtherstellung und bei Fotini Petraki für die experimentelle Unterstützung mit XAS sowie wertvolle Diskussionen. Wir danken Dr. Fabrizio Santoro für gewinnbringende Diskussionen im Hinblick auf die Simulation resonanter Ramanschwingungen. Die optischen Experimente wurden von der Deutschen Forschungsgemeinschaft unterstützt durch ZH 279/13-1, ZH 279/15-1, ZH 279/16-1, ME 1600/21-1, ME 1600/23-1, PE 546/17-1. Die Arbeit in Madrid wurde vom spanischen Ministerium für Wissenschaft (MINECO–FEDER project PID2022-138222NB-C21), dem „Severo Ochoa“ Programm für Exzellenzzentren in Forschung und Entwicklung (MINECO grant CEX202-000103-9S) und dem Campus internationaler Exzellenz UAM+CSIC unterstützt. Teile der theoretischen Arbeit wurden durch das Projekt ZR2022MA059 von der Naturwissenschaftsstiftung der Provinz Shandong unterstützt. Wir bedanken uns für die Unterstützung durch das Land Baden-Württemberg durch bwHPC und die Deutsche Forschungsgemeinschaft durch INST 40/575-1 FUGG (JUSTUS 2 cluster). Wir danken dem Helmholtz-Zentrum Berlin (BESSY II) für die Bereitstellung von Synchrotronstrahlung an der Strahllinie PM4.
Open Access Veröffentlichung ermöglicht und organisiert durch Projekt DEAL.
Interessenkonflikt
Die Autoren erklären, dass keine Interessenkonflikte vorliegen.
Erklärung zur Datenverfügbarkeit
Die Daten, auf denen die Ergebnisse dieser Studie aufbauen, sind auf begründete Anfrage hin von den Autoren erhältlich.




