Bayesian Inference for Model Analyses of Supramolecular Complexes: A Case Study with Nanocarbon Hosts
Abstract
A 126 π-electron nanobowl molecule, phenine tridehydrosumanene, was synthesized in 12 steps through the development of a polygon cyclization strategy that assembled the polygonal precursors by Ni-mediated macrocyclization. The bowl-shaped structure accommodated C70 as a guest at the concave site, and the ball-in-bowl structure was determined by X-ray crystallography. The host–guest equilibrium in solution was studied with titration experiments using isothermal calorimetry, which provided an interesting test case for studying the host–guest stoichiometry. Bayesian inference was introduced for stoichiometric analyses of the equilibrium, and a procedure to estimate the volume of prior probability in the parameter space was developed. The Bayesian procedure functioned as Occam's razor and provided quantitative support for a specific stoichiometry. The method was examined with five host–guest examples comprising nanocarbon hosts, which suggested the versatility of Bayesian inference for studies of supramolecular complexes.
Deciding a model for chemical reactions is an important step in elucidating the kinetic and/or thermodynamic characteristics of processes with quantitative parameters. In particular, thermodynamic analyses of host–guest equilibria allow us to characterize and reveal the roles of weak interactions in the complexes.1 For thermodynamic analyses of host–guest equilibria, inference of the ratio between the host and guest, i.e., the stoichiometry (n:m in Figure 1a), has become a difficult yet interesting subject. A traditional method, the continuous variation method (Job plot),2 is considered obsolete, and various methods are being proposed to aid stoichiometry inference.3 In our own studies with nanocarbon hosts,4 we found quantitative methods to be superior in enabling discussion based on firm evidence and first adopted statistical F-test/P-value measures at the fitting stage to derive association constants (K; stage 2 in Figure 1a).5 Noticing the inapplicability of F-test evaluations for complicated host–guest systems, we next introduced Akaike's information criterion (AIC) from information theory and determined its usefulness in some cases.6, 7 Although another procedure was introduced to quantitatively evaluate the models at a different stage to derive thermodynamic parameters (ΔH, ΔS; stage 4 in Figure 1a),8 this new procedure, named van ′t Hoff (vH) validation, assumed temperature-independent enthalpy and entropy for the evaluation8, 9 and was therefore inapplicable for modern methods, such as isothermal calorimetry (ITC), that directly measure the experimental enthalpy.10 In this study on a bowl-shaped nanocarbon host, we introduce a novel measure from Bayesian statistics for model analyses as a versatile fitting method (stage 2).

Curve fitting analyses of titration experiments with various equilibrium models. (a) Procedures to determine association constants and thermodynamic parameters. Chemical models were decided either at stage 2 or stage 4 by model comparisons. (b) Outline of the fitting analyses. As an example, comparisons of the 1 : 1, 1 : 2 and 2 : 1 ratios are shown. (c) Measures for stoichiometry inference at stage 2.
Before describing the experimental details, common analyses at the fitting stage are outlined. After performing titration experiments (stage 1), the titration data are respectively fitted by the least-squares method with multiple equations corresponding to stoichiometry models (stage 2). As shown with an example used to compare the 1 : 1, 1 : 2 and 2 : 1 models (eq. 1–3; Figure 1b),11 the distances between the actual data and each fitting curve are calculated as the sum of the squared residuals (SS) and the normalized form of goodness-of-fit value, R2. These goodness-of-fit measures clarify the mathematical obstacles at this stage.12, 13 When the titration data are fitted with more complicated models (e.g. 1 : 2 or 2 : 1) with more parameters in the fitting equations (e.g. K1 and K2), the goodness-of-fit measures inevitably suggest “better fits” than the simpler model (e.g. 1 : 1 with K1). Therefore, when the stoichiometry models are to be compared at this fitting stage, the introduction of alternative measures is necessary. The information-theoretic approach of the AIC measure adds a penalty term (2k in eq. A, Figure 1c) for the comparisons,14, 15 which plays a role of Occam's razor in this approach. Although this AIC approach is concise and feasible for chemists,6 the penalty term has been found to be insufficient in some cases including the present studies with a bowl-shaped host. Recently, Bayesian inference has become popular and influential, particularly for machine-learning studies,16, 17 which demonstrates the usefulness of prior knowledge in deciding models. Although Bayesian inference was computationally demanding, in 2022, Dunstan and co-workers introduced an easy computational method18 based on MacKay's method of Bayesian interpolation.19 In this method, the marginal likelihood integral (MLI) is calculated by incorporating the prior probability via the so-called Occam factor (eq. B, Figure 1c). Thus, by adopting a parameter range ( ) to consider prior knowledge, MLI values for muon-spin spectra or GaAs band gaps were obtained for model inference. In this study, we developed a procedure to obtain the parameter range for fitting analyses of host–guest equilibria at stage 2, which consequently afforded MLI values to indicate the preference of one model over the others.
This study began with the synthesis of a nanometer-sized bowl-shaped molecule that served as an interesting host for studies of stoichiometric models. As an AIC-inapplicable bowl-shaped host,8 phenine corannulene was found in the preceding study via the synthesis with our omphalos strategies (Figure 2a).20, 21 In this work, a larger phenine bowl, phenine tridehydrosumanene (1),22 was designed and synthesized by developing a polygon cyclization strategy. Thus, a monomeric precursor (2) was coupled with dibromobenzene (3) via twofold Suzuki–Miyaura coupling to afford terphenyl (4).23 After Miyaura borylation of 4,24 quinquephenyl (7) was obtained through coupling with 6, which was converted to the polygonal unit [5]cyclo-meta-phenylene ([5]CMP, 8) by Ni-mediated Yamamoto coupling.25, 26 The [5]CMP precursor was converted to 11, which has two phenyl groups, by a 2-step transformations including C−H borylation27 and Suzuki–Miyaura coupling. After furnishing the precursor with iodine coupling linkers, polygon cyclization was performed by Yamamoto coupling. The trimerization of 12 thus proceeded in an efficient manner to afford cyclic trimer 13 with a [6]CMP core in 64 % yield, which was much higher than the yield for hexamerization of dibromobenzene.26 A few attempts have been made with the final ring-closing reactions at the periphery. A borylated precursor (14) from C−H borylation was first subjected to cyclization reactions such as Pt-mediated and Pd-catalyzed coupling,28, 29 but none of them afforded the desired compound. Considering the previous success of Yamamoto coupling in strain-inducing cyclizations,21 we then examined threefold Ni-mediated coupling reactions after converting 14 to an iodinated precursor (15).30 Although the reaction was sluggish and contaminated with byproducts, the 126π target compound phenine tridehydrosumanene (1) was finally obtained in 18 % yield.31 From a commercially available benzene derivative, the total yield of 1 was 1.7 %, and 27 biaryl bonds were formed. The efficiency of biaryl bond formation for the overall 12-step transformation was thus 86 %.
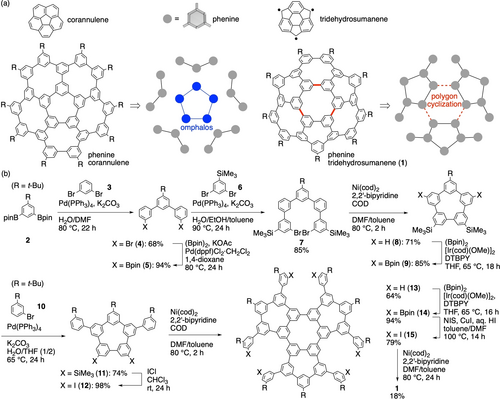
Bowl-shaped phenine nanocarbon molecules. (a) Synthetic strategies: an omphalos strategy for phenine corannulene and a polygon cyclization strategy for phenine tridehydrosumanene (1). (b) Synthesis of 1.
Due to their curved π-systems with large concave surface areas, bowl-shaped hosts provide interesting test cases for studies of stoichiometry inference.8 In the present study, we found that tridehydrosumanene (1) captured [70]fullerene (C70) in solution, which led us to explore the stoichiometry inference of the bowl-shaped host. We first found by recording 1H NMR spectra that host–guest complexation between 1 and C70 proceeded (Figure S3 in Supporting Information). However, the titration experiments were not successful due to the low solubility of C70, which prevented reliable, quantitative evaluations of the equilibrium. We then adopted ITC for the titration experiments and developed a procedure to introduce Bayesian inference for comparisons of the stoichiometry models. First, the titration experiments were performed in triplicate in a standard manner (Figure 3a). Second, each titration dataset was independently fitted to derive preliminary K and ΔH values by using equations for all the possible models (eq. 1–3 in this study), and these preliminary values were adopted as prior knowledge for the Bayesian MLI calculations. Third, as shown in eq. B, we calculated the prior volume term ( ): by multiplying the range of preliminary K/ΔH values (Kmax–Kmin; ΔHmax–ΔHmin), the volume was obtained. Finally, triplicate titration data were combined and globally fitted. By using outputs such as SS and det Covp from the fits, goodness-of-fit evaluations and model comparisons with AIC and MLI were performed. Each measure afforded values of the evaluations, which were conveniently compared in visual form with pie charts by using the weights (wi) of the values (R2 wi, Akaike wi, Bayes wi; Figure 3b).32 The charts showed that the Bayes wi value supported the 1 : 1 model and that the Akaike wi value supported the 1 : 2 model. As shown in Table 1, large standard deviations were found for the parameters obtained for the 1 : 2 and 2 : 1 models. Thus, we concluded that a 1 : 1 ball-in-bowl complex (1⊃C70) was formed upon mixing 1 and C70 in solution, which was quantitatively supported by the Bayesian inference with the highest Bayes wi values.
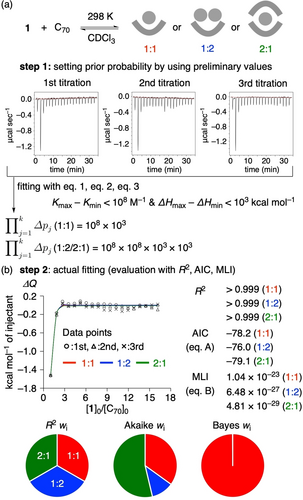
Host-guest complexation between 1 and C70. (a) Titration experiments and preliminary values used in setting the prior probability. (b) Fitting and evaluations.
model |
parameter[a] |
support |
|---|---|---|
1 : 1 |
K1=(1.4±0.6)×106 ΔH1=−1.8±1.0 (−TΔS1=−6.6±1.2) |
Bayes wi=0.999 |
1 : 2 |
K1=(5.8±19.5)×106 K2=(1.6±44.7)×103 ΔH1=−0.3±1.7 ΔH2=−140.1±3495.8 (−TΔS1=−10.9±3.7) (−TΔS2=−144.5±3512.4) |
none |
2 : 1 |
K1=(1.7±0.7)×106 K2=10.6±779.2 ΔH1=−1.72±0.08 ΔH2=−28.1±2047.9 (−TΔS1=−6.8±0.3) (−TΔS2=26.7±2091.5) |
Akaike wi=0.537 |
cf. 1 : 1 for phenine corannulene⊃C70 |
K1=(1.48±0.04)×106 ΔH1=−3.1±0.2 (−TΔS1=−5.3±0.2) |
vH validation Bayes wi=0.999 (See below) |
- [a] Two sets of parameters (K and ΔH) are derived from the fitting, which consequently affords ΔS values. T=298 K. Units=K: M−1, ΔH: kcal mol−1, −TΔS: kcal mol−1.
The structural differences of the two bowl-shaped hosts, i.e., phenine corannulene and phenine tridehydrosumanene (1), resulted in subtle differences in the thermodynamic parameters as shown in Table 1. For instance, two association constants were essentially identical at 106 M−1. However, we found interesting differences in the dynamic behavior. Thus, in the 1H NMR spectra, 1 showed independent resonances for the unbound host and complexed host in the presence of C70, whereas phenine corannulene showed time-averaged merged resonances (Figure S4 in Supporting Information). As we observed that complexation between 1 and C70 was more biased toward entropy control, we concluded that the solvation/desolvation dynamics with 1 were slowed.
The 1 : 1 ball-in-bowl structure of 1⊃C70 was confirmed with a crystallographic analysis (Figure 4). The single crystal was obtained from a 1 : 1 mixture of 1 and C70 in chloroform at 25 °C while diffusing vapor of methanol. The bowl-shaped host captured one C70 molecule at the concave center, and the periphery was bent to secure the guest.33 Detailed structural analyses with curved phenine normal vectors (CPNVs)34 revealed that the central hexagon was contorted, whereas the peripheral regions were relatively free of structural distortions (Figure S6 in Supporting Information). In-depth analyses of the molecular Gauss curvature with discrete surface theory35 showed that the phenine panels located in the central hexagon exhibited positive Gauss curvature (Figure S7 in Supporting Information), which confirmed the presence of a bowl shape in the phenine tridehydrosumanene host.
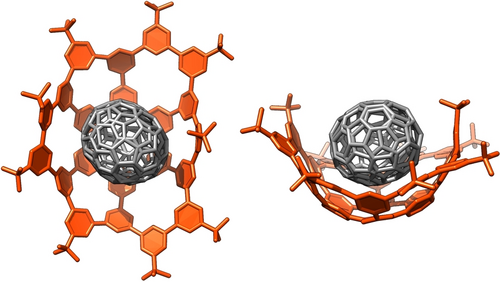
Crystal structure of the 1 : 1 ball-in-bowl complex 1⊃C70. Additional structural details are provided in Supporting Information.
Finally, the Bayesian inference was examined with other host–guest complexes of nanocarbon hosts (Figure 5). In previous study, a ball-in-bowl complex of phenine corannulene⊃C60 was found as a difficult case to be examined by AIC measures.8 In this study, a similar ball-in-bowl complex of phenine corannulene with C70 was examined by NMR titration experiments (See Figure S8 in Supporting Information). The Akaike wi value supported a 1 : 2 stoichiometry at 298 K, whereas the Bayes wi value supported a different stoichiometry of 1 : 1. Performing variable-temperature titration experiments from 283 K to 323 K, we then examined the stoichiometry with the vH validation method to find supports for the Bayes-supported 1 : 1 stoichiometry.36 The present method of Bayesian inference was further applied to three other systems by using previously reported titration data of the tubular hosts (P)-(12,8)-[4]cyclo-2,8-chrysenylene ([4]CC)6, 37 and (P)-(12,8)-[4]cyclo-2,8-anthanthrenylene ([4]CA).38 For these systems with fullerene guests, the stoichiometries that were suggested by crystal structures were supported both by the Akaike and Bayes wi values. Interestingly, the host–guest system of [4]CC⊃C70 showed that the wi value of 1 : 1 from the Bayesian inference was greater than that from the AIC, which might indicate that the penalty used to avoid overfitting may be more effective with the present Bayesian procedure that takes account of the prior probability.18
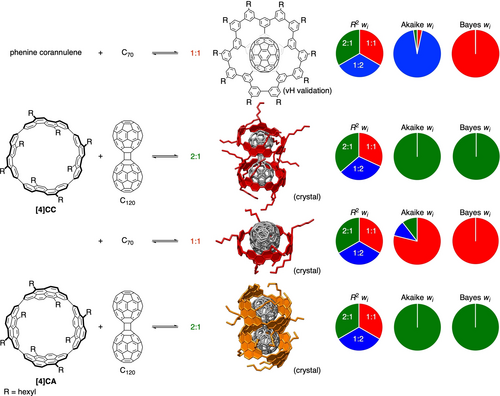
Bayesian inference analyses of stoichiometric models with nanocarbon hosts. The titration data of the tubular hosts were derived from literatures: [4]CC⊃C120=ref. [37], [4]CC⊃C70 and [4]CA⊃C120=ref. [38].
In summary, we synthesized a bowl-shaped molecule with a 126π tridehydrosumanene skeleton composed of phenine networks. The polygon cyclization synthetic strategy enabled concise 12-step construction of a nanometer-sized, contorted skeleton by forming 27 biaryl linkages via coupling. The bowl-shaped structure served as a host to capture C70 as a guest, which provided an interesting test case with which to examine Bayesian inference in supramolecular host–guest chemistry. A method was introduced to incorporate prior probabilities for fitting analyses of host–guest equilibria, which functioned as Occam's razor in examining the stoichiometric models. Consequently, a 1 : 1 association between phenine tridehydrosumanene and C70 was revealed with the Bayesian wi value as a supporting criterion. The 1 : 1 ball-in-bowl structure was unequivocally disclosed by X-ray crystallography, which also revealed details of the contorted structures with geometrical measures. Finally, the Bayesian procedure was examined with other supramolecular complexes containing nanocarbon hosts, which revealed the usefulness and reliability of the Bayesian inference in addition to other measures including Akaike's information criterion. Since there could be no single method to provide decisive conclusions, examining stoichiometry models with multiple criteria is necessary and important,39, 40 and the present Bayesian procedure should be a versatile method for use with many other systems.
Acknowledgments
Y.O. thanks MERIT-WINGS program for the predoctoral fellowship. We were granted access to X-ray diffraction instruments in KEK (BL17A, no. 2022G596). This work was partly supported by KAKENHI (20H05672, 22H02059, 22K20527) and JST ACT-X (JPMJAX23DI). We wish to thank Prof. D. J. Dunstan (Queen Mary University of London) for helpful information on Bayes factor calculations and Prof. E. Kurozumi (Hitotsubashi University) for providing valuable information for the statistical analyses.
Conflict of interests
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available in the supplementary material of this article. The crystal data that support the findings of this study are openly available in CCDC at https://www.ccdc.cam.ac.uk/data request/cif, reference number 2340188.




