All-Optical Spin–Orbit Coupling of Light in Coherent Media Using Rotating Image

1 Introduction

The effect of spin–orbit coupling (SOC) is shown to exist in various physical systems, which has generated great excitement in many fields of physics, such as the spin-Hall effect1 or topological insulators2, 3 in solid materials and engineered SOC in ultracold atoms.4 For the studies of SOC of light, a number of efforts have been directed toward the spin-controlled manipulation of light wave at the subwavelength scale,5 thereby increasing the information processing capabilities of optical systems by providing additional degrees of freedom.

To improve the processing efficiency of quantum information, storage, and retrieval of 2D image in coherent media based on electromagnetically induced transparency (EIT)6-8 have been actively investigated for decades, with potential importance for high-dimensional quantum memory and multi-qubit operations.9-16 In addition to practical applications, 2D image in a slow-light coherent medium has also proven to be a unique setting to visualize relativistic effects, such as rotary photon drag,17 being of special interest in fundamental physics.

Very recently, an all-optical scheme of SOC of light has been proposed based on the propagation dynamics of a spinor image through a rotating slow-light EIT medium,18 providing an optical analog of a quantum system with relativistic corrections. In the proposal, a rotating cold atomic ensemble in a Mott insulator phase was examined, which could provide a tunable platform to generate and manipulate the SOC of light without requiring subwavelength control as reviewed in ref. [5]. However, limited by the low rotation frequency of cold atoms (up to a few tens of Hz), such an experimental implementation can hardly give rise to large SOC splitting of light.

In this article, we propose an alternative method to realize all-optical SOC of light in an EIT-based slow-light medium using rotating image, which may greatly enhance the spin–orbit interaction of light over a broad range of parameters. Based on our theoretical model, it is found that the paraxial wave equation of a rotating spinor image can mimic the Pauli equation describing a spin-1/2 quantum field with strong SOC, where the spin-up and -down states have different effective masses. We also perform the numerical simulations by using realistic parameters relevant to the EIT experiments with a Gaussian control beam and a radially inhomogeneous atomic density of comparable width. To the best of the author's knowledge, a combination of spatially dependent control laser field as well as atomic density distribution has not yet been considered for the all-optical SOC of light. The results indicate that significant spatial separation (i.e., strong SOC splitting) of the spin states can be achieved in the radial direction with high tunability. Our proposal may help extend the experimental feasibility of manipulating and visualizing the all-optical SOC of light in an EIT medium.

2 Theoretical Model and Analyses

As a matter of fact, in an early “ether-drag” experiment by using bulk material with weak dispersion (e.g., a quartz glass bar),19 because it is too difficult to rotate the glass bar with MHz frequency, a moving-image scheme was instead employed to achieve significant rotary photon drag. Using the same strategy, we here consider the propagation dynamics of a rotating spinor image through an EIT medium, where the possible experimental setup is shown in Figure 1. For details, in Figure 1a, a petal-shaped spinor image can be generated in the probe field by interfering two Laguerre–Gaussian (LG) beams with opposite orbital-angular-momentum (OAM) indices (i.e., $\pm \ell$ with ℓ a positive integer).20

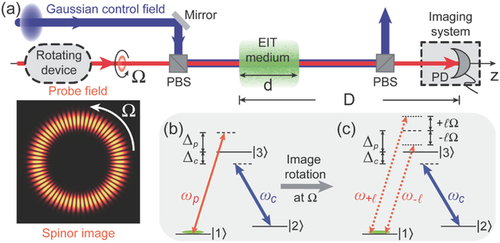
To rotate the image at the frequency of Ω, two approaches can be employed. i) One can pass it through a rotating Dove prism with a frequency of $\mathrm{\Omega }/2$ and thus the rotational Doppler shifts of the $\pm \ell$ LG modes in the spinor image are $\pm \ell \mathrm{\Omega }$, respectively.21 In practice, the Dove prime can be mechanically driven by a motor at the operating speeds up to 10 000 rev min⁻¹ (≈167 Hz).22 ii) One can also introduce frequency shifts $\pm \ell \mathrm{\Omega }$ to the $\pm \ell$ modes, respectively, using acousto-optic modulators, where the rotation frequencies of the image can range from a few mHz to hundreds of MHz.19, 23

Note that, for the rotation operations, because the polarization does not necessarily rotate with the intensity pattern of the image, the contribution of polarization to the frequency shift can be excluded.19, 21, 23 Thus, we can assume that the probe and control fields have opposite circular polarizations and copropagate along the z direction. In practice, the control field has an inhomogeneous intensity profile, such as a Gaussian beam. And, the cold atomic cloud also has a radially varying density distribution (e.g., a Gaussian shape) in a magneto-optical trap.24 Both types of the inhomogeneity will be included in our scheme.

The form of the $\zeta \widehat{\ell }{\widehat{\sigma }}_z$ term in Equation 10 suggests that a spin-degenerate level can be split by SOC into levels with spin parallel and antiparallel to the orbit. To simulate the SOC of an electron with the orbital motion in a centrally symmetric field, we consider that the intensity of the control field is inhomogeneous in the radial direction, for instance, a Gaussian beam. Moreover, cold atomic ensembles with high density has been successfully realized in a magneto-optical trap.24 The atomic density profile $n_a$ is also inhomogeneous and usually could be simply described by a Gaussian function in the radial direction. Therefore, the SOC strength ζ is a function of the radius r (i.e., $\zeta (r)\propto n_a(r)/{\mathrm{\Omega }}_c^2(r)$) in the transverse direction, mimicking the central potential.

As a result, the SOC term $\zeta \widehat{\ell }{\widehat{\sigma }}_z$ can lift the spatial degeneracy of quantum states with the same orbital wave function $e^{i\ell \varphi }$ but opposite spins $|{\pm }_z⟩$. For the spinor image, such a degeneracy removal corresponds to the spatial separation of the LG modes in real space. Thus, the solution of the paraxial propagation Equation 10 closely resembles the SOC splitting of an orbital electron moving in a central potential in 2D.

3 Numerical Results

In what follows, some realistic EIT parameters close to those measured in experiments are used to perform the numerical simulations. Moreover, for the probe field, we choose the LG modes with high OAM indices $\pm \ell =\pm 32$ in the input spinor image. The radial evolution of the $\pm \ell =\pm 32$ LG modes can mimic the SOC splitting of the spin $|{\pm }_z⟩$ states, where the high OAM index ℓ can strengthen the spin–orbit interaction.

Considering a cloud of cold atoms in the magneto-optical trap,24 we assume that the peak atomic number density is ${\mathring{n}}_a\approx {10}^{12}$ cm⁻³ and the the transverse Gaussian density profile is given by $n_a(r)={\mathring{n}}_a\exp (-r^2/{w_a}^2)$ with $w_a$ being the $1/e$ radius, where we set $w_a=150$ µm. To fit the LG beams into the small atomic cloud, we assume that the waist of the beams is $w_0=25$ µm in Equation 11.

We also use the D1 transition of ⁸⁷Rb as an example to construct the EIT system, where the $|5^2{S}_{1/2},F=2,m_F=+2⟩$, $|5^2{S}_{1/2},F=2,m_F=0⟩$, and $|5^2{P}_{1/2},F^{\prime }=1,m_{F^{\prime }}=+1⟩$ Zeeman sub-levels represent the $|1⟩$, $|2⟩$, and $|3⟩$, respectively. Thus, we have the probe and control wavelengths ${\lambda }_p\approx {\lambda }_c\approx 795$ nm, the decay rates ${\gamma }_{21}=2\pi \times 1$ kHz and ${\gamma }_{31}=2\pi \times 6$ MHz, and the dipole moment ${\mu }_{13}=2.54\times {10}^{-29}$ C m.29 Moreover, the Rayleigh range $z_R$ of the LG mode in the spinor image is used as the unit of the propagation distance D of the image (see Figure 1a) in the following numerical calculations, where $z_R$ is approximately equal to $\pi w_0^2/{\lambda }_p\approx 2.47$ mm. The control field is set to be a Gaussian beam and its Rabi frequency is expressed by ${\mathrm{\Omega }}_c={\mathring{\mathrm{\Omega }}}_c\exp (-r^2/{w_c}^2)$ with the peak Rabi frequency ${\mathring{\mathrm{\Omega }}}_c$ and the waist width $w_c$.

First, we consider a case with low-speed rotation for the spinor image, for example, $\mathrm{\Omega }=100$ Hz. In practice, such a low rotation frequency could be generated by passing the image through a rotating Dove prism, where the mechanical rotation frequency of the prism is 50 Hz. Because the rotation frequency is low, to achieve strong SOC splitting, one need to enhance the SOC strength $\zeta =(n_g-1)\mathrm{\Omega }/c$ by generating large group refractive index. Therefore, a relatively weak control field (${\mathring{\mathrm{\Omega }}}_c=0.4{\gamma }_{31}$) is applied to create a narrow EIT window, where the waist width of the control field is assumed to be $w_c=100$ µm, smaller than that of the atomic cloud $w_a$.

Note that we take the decay rate of the upper level $|3⟩$ (i.e., γ₃₁) as the unit of the Rabi frequency of the control laser, which is defined by ${\mathrm{\Omega }}_c={\mu }_{13}{E}_c/(2\hslash )$ with $E_c$ the electric field of the control laser. To show the realistic parameters relevant to the EIT experiments, we can use the expression $I_c={\epsilon }_{0}c{E}_c^2/2$ to obtain the intensity of the control field. Because the control field is assumed to be Gaussian in our scheme, the total power of the Gaussian control beam can be given by $P_c={\mathring{I}}_c\pi w_c^2/2$, where ${\mathring{I}}_c=2{\epsilon }_{0}c{\hslash }^2{\mathring{\mathrm{\Omega }}}_c^2/{\mu }_{13}^2$ is the peak intensity and $w_c=100$ µm is the waist width of the control beam. When the peak Rabi frequency of the control field is ${\mathring{\mathrm{\Omega }}}_c=0.4{\gamma }_{31}$, we can calculate the peak control intensity as ${\mathring{I}}_c=2.1$ mW cm⁻² and estimate the control power $P_c=0.33$ µW in the case with low-speed rotation $\mathrm{\Omega }=100$ Hz. Such a control intensity can be generated by commercial semiconductor laser diodes and has been considered in EIT-based light storage experiment with cold atoms.30

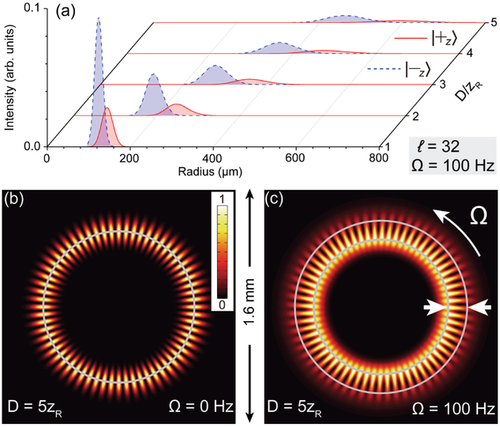
In Figure 2, we show the spatial evolution and distortion of the spinor image with low rotation frequency (i.e., $\mathrm{\Omega }=100$ Hz) passing through the EIT medium. In Figure 2a, strong radial splitting is clearly illustrated for the $\pm \ell =\pm 32$ LG modes (equivalent to the spin-up and -down states $|{\pm }_z⟩$). To quantitatively compare the cross sections in Figure 2a in the presence of absorption and diffraction, we normalize the peak intensity of each input LG mode given by Equation 11. To clearly show the 2D intensity profiles at the photon detector in Figure 2b,c, we also normalize their peak intensities to see the spatial variations of the interference fringes in details. Without rotation, the transmitted image in Figure 2b is still petal-shaped because the two LG modes totally coincide with each other in space at the photon detector. However, upon rotation, the SOC can split the spin-up and -down wave functions due to the gradient of the group refractive index in the radial direction. Owing to the removal of the spatial coincidence (degeneracy), a ferris-wheel pattern in Figure 2c can be observed. Based on the EIT parameters used in Figure 2, the modulation range of the group refractive index and the delay time for the spinor image traveling through the EIT slow-light medium can also be estimated, where we have the group refractive index $n_g\gtrsim 3.6\times {10}^6$ (see Equation 7 for $n_g$) and the time delay ${\tau }_d\approx n_{g}d/c\gtrsim 24$ µs.8

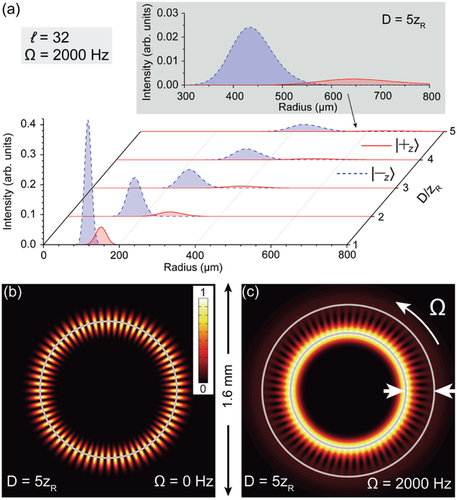
To further enlarge the SOC splitting, we also increase the rotation frequency of the spinor image to $\mathrm{\Omega }=2000$ Hz. For such a high rotation frequency, mechanically rotating a Dove prism is not applicable, while an acousto-optic modulator can be used to introduce frequency shifts $\pm \ell \mathrm{\Omega }$ to the $\pm \ell$ LG modes. To alleviate the absorption, the peak control Rabi frequency (i.e., the control intensity) is raised to ${\mathring{\mathrm{\Omega }}}_c=1.4{\gamma }_{31}$ and other EIT parameters are unchanged. Thus, the peak control intensity is ${\mathring{I}}_c=25.5$ mW cm⁻² and the corresponding control power is $P_c=4.01$ µW, which can be emitted from a commercial laser diode.30 Again, based on the expression of the SOC strength $\zeta =(n_g-1)\mathrm{\Omega }/c$ with $n_g\approx 1+\kappa {\omega }_p/(2{\mathrm{\Omega }}_c^2)$, we can directly compare the SOC strength ζ in the above two cases and find that the ζ value in the high-speed rotation case is ≈1.6 times larger than that in the low-speed case shown before.

Our numerical results in Figure 3 straightforwardly reflect such enhancement, where the SOC splitting for $\mathrm{\Omega }=2000$ Hz is larger than that for $\mathrm{\Omega }=100$ Hz in Figure 2. As seen, the radial splitting in Figure 3a is greatly enhanced so that the spatial overlap of the $|{\pm }_z⟩$ wave functions becomes very small. Consequently, compared with the nonrotating case in Figure 3b, a dual-ring structure appears in Figure 3c, where a photon detector with high sensitivity (e.g., an electron multiplying CCD15) can be used to observe the transmitted image with low intensity. In addition, for Figure 3, the modulation range of the group refractive index is $n_g\gtrsim 2.94\times {10}^5$ and the delay time of the spinor image is ${\tau }_d\gtrsim 1.96$ µs.

4 Discussions

Note that the two LG modes do interfere in real space, thus generating the interference fringes. On the contrary, for the spin-up and -down states of a real orbiting electron, they do not interfere due to their orthogonality in spin space. However, in our scheme, we only concern the radial intensity splitting of the spinor image consisting of the $\pm \ell$ LG modes because it can resemble the SOC splitting of the spin-up and -down $|{\pm }_z⟩$ wave functions in real space along the radial direction, whereas the spatial spin texture is not involved in our scheme. On the other hand, for experimental measurements, the 2D interference patterns can also help characterize the spatial separation, as shown by the visible distortion of the image from a petal-shaped pattern in Figures 2b and 3b without splitting, to a ferris-wheel pattern in Figure 2c with moderate splitting, or to a dual-ring structure in Figure 3c with large splitting.

By analogy, the SOC splitting can also be regarded as a result of the OAM-based all-optical Stern–Gerlach effect of light, whereby different OAM quantum states can be spatially separated along the external light field gradient as well as the atomic density gradient in the radial direction. Therefore, opposite radial phase modulations can be imposed onto the $\pm \ell$ LG modes, that is, one mode is focused and the other is defocused, while the azimuthal phase winding of each mode is preserved. Such a result may offer intriguing possibilities for an all-optical and nondestructive sorting technique for the spatial multiplexing of OAM quantum states of photons.

In general, our numerical results using realistic EIT parameters are consistent with our theoretical analyses based on an ideal EIT model in Section 2. This means that the absorption has negligible influence on the spatial evolution of the spinor image. Therefore, because the large group refractive index plays a dominant role in a realistic EIT system, our theoretical proposal for the connection between the paraxial propagation of a rotating spinor image (i.e., Equation 8) and the SOC of an orbiting electron (i.e., Equation 10) in Section 2 is valid, where both the inhomogeneous control intensity and atomic density together mimic the central potential in a 2D atom.

Moreover, we use higher mode of OAM in the spinor image in our numerical calculations due to the following two reasons. On one hand, in theory, based on Equation 9, one can see that the term $\zeta \ell$ before ${\widehat{\sigma }}_z$ actually plays a role as an effective magnetic field. Higher OAM index ℓ may create stronger effective magnetic field, which can thus lead to more significant spin–orbit interaction in Equation 10. On the other hand, in practice, if a rotating Dove prism is used to mechanically rotate the spinor image, the mechanical rotation of bulk material with high frequency is very difficult (up to ≈167 Hz).22 To obtain larger rotational Doppler shift $\mathrm{\Omega }\ell$ for the LG modes to facilitate the experimental observation of the SOC splitting, higher OAM index ℓ of the LG mode is expected.

Furthermore, in principle, besides the Gaussian control field, due to the rotational invariance, a high-order LG control field with a ring-shaped intensity pattern can also equivalently lead to a spatially varying central potential in the Pauli equation (i.e., Equation 10) for the spin 1/2 quantum particle in our scheme. (Note that, to simplify our discussion, we assume that the high-order LG control field has the OAM index $\ell \ge 1$ but the radial mode index $p=0$, i.e., a single-ring structure.) By analogy with the fine-structure theory in atomic spectra, the SOC in such a central potential with radial gradient in our scheme can lift the degeneracy of the spin states and thus spatially separate the spin-up and -down states in 2D as well. More straightforwardly, from the viewpoint of propagation dynamics of the spinor image in the EIT medium, the two LG components in the probe field can undergo opposite radial phase modulations (see the susceptibilities $\chi ({\omega }_{\pm \ell })$ in Equation 7) due to the radial gradient of the control intensity. In other words, if the spinor image in the probe field travels through the region where the LG control field has steeper intensity gradient in the EIT medium, the effect of focusing one probe LG mode but defocusing the other one could occur more significantly, thus enhancing the SOC splitting of light for experimental observation. Therefore, in practice, one should carefully provide the coincidence of axes of the spinor image and the LG control field, and then adjusts their waist widths to make sure that the spinor image experiences steep radial gradient of the LG control intensity in the EIT medium. Meanwhile, owing to the transverse inhomogeneity of the LG control intensity, it also should be noted that the control Rabi frequency that the spinor image experiences in the medium should satisfy the condition ${\mathrm{\Omega }}_c^2\gg \ell \mathrm{\Omega }{\gamma }_{31}$ in our scheme. In a more inspiring way, because high-order LG modes usually have steeper intensity gradient in their ring-shaped intensity structures (i.e., thinner bright rings), they may generate larger spatial splitting or even more complicated diffraction patterns for the transmitted spinor image, which definitely deserves further study for the SOC dynamics of light in EIT media.

Finally, we would like to clarify the significance of our present work. In the previous work in ref. [18], we showed the possibility of all-optical SOC of light using a rotating EIT medium. Although the rotating medium could be generated by using the atomic Mott insulator (MI) in a rotating optical lattice, the implementation of rotating atomic MI is very challenging in experiments. Moreover, the size of the atomic MI is small, the rotation frequency is low, and the configurations of the rotating lattice beams are complicated. These factors together may cause difficulties in precisely controlling the EIT system and prevent achieving large SOC splitting. To promote further explorations, we here propose and rigorously prove that a rotating image could be an alternative to greatly enhance the spin–orbit interaction of light. The rotating image with the rotation frequency ranging from mHz to MHz supplies a practical solution to achieve highly tunable and even visible SOC splitting of light (see Figures 2 and 3) and also overcomes all the difficulties in the rotating EIT medium. Our present work provides a remarkable extension of the mechanism of all-optical SOC of light based on existing experimental parameters, constituting not only a technical but also a conceptual advance in understanding and realizing all-optical SOC of light. The results represent a critical step toward the experimental implementation in realistic EIT media, which can further stimulate both theoretical and experimental interests and efforts to achieve a variety of SOC-related effects of light even in other types of EIT-based systems (e.g., see ref. [31]).

5 Conclusion

In conclusion, we have shown that the paraxial propagation of a dual-frequency and dual-mode spinor image through an EIT medium can bear close resemblance to the SOC dynamics of an orbiting electron in a 2D atom, where the oppositely oriented $|{\pm }_z⟩$ spin states have different effective masses. The rotating-image scheme with atoms at rest avoids the technical challenge of rotating cold atoms in optical lattices as a bulk material. Therefore, strong and tunable SOC splitting can be observed over a large parameter range in realistic EIT systems with radially inhomogeneous control field and atomic density. Our findings thus pave a convenient pathway for direct visualization of a quantum system with relativistic corrections based on quantum-optical analogy, which may hold promise for a new degree of freedom for controlling spin–orbit physics of light as well as spatial multiplexing systems for quantum information processing.

Conflict of Interest

The author declares no conflict of interest.