Testing the equivalence of modern human cranial covariance structure: Implications for bioarchaeological applications
This article was published online on 30 June 2016. An error was subsequently identified. This notice is included in the online and print versions to indicate that both have been corrected on 20 July 2016.
Funding Information: This research was supported by the Research Foundation for the State University of New York.
Abstract
Objectives
Estimation of the variance-covariance (V/CV) structure of fragmentary bioarchaeological populations requires the use of proxy extant V/CV parameters. However, it is currently unclear whether extant human populations exhibit equivalent V/CV structures.
Materials and Methods
Random skewers (RS) and hierarchical analyses of common principal components (CPC) were applied to a modern human cranial dataset. Cranial V/CV similarity was assessed globally for samples of individual populations (jackknifed method) and for pairwise population sample contrasts. The results were examined in light of potential explanatory factors for covariance difference, such as geographic region, among-group distance, and sample size.
Results
RS analyses showed that population samples exhibited highly correlated multivariate responses to selection, and that differences in RS results were primarily a consequence of differences in sample size. The CPC method yielded mixed results, depending upon the statistical criterion used to evaluate the hierarchy. The hypothesis-testing (step-up) approach was deemed problematic due to sensitivity to low statistical power and elevated Type I errors. In contrast, the model-fitting (lowest AIC) approach suggested that V/CV matrices were proportional and/or shared a large number of CPCs. Pairwise population sample CPC results were correlated with cranial distance, suggesting that population history explains some of the variability in V/CV structure among groups.
Discussion
The results indicate that patterns of covariance in human craniometric samples are broadly similar but not identical. These findings have important implications for choosing extant covariance matrices to use as proxy V/CV parameters in evolutionary analyses of past populations.
1 Introduction
Investigations of evolutionary processes and population relatedness in bioarchaeology are impeded by the fragmentary nature of skeletal remains and small sample sizes. This often makes it difficult, if not impossible, to accurately estimate the underlying biological variance/covariance (V/CV) structure of a prehistoric population (Jantz & Owsley, 2001). In evolutionary quantitative genetics, the genetic V/CV matrix (commonly referred to as the G-matrix) is a fundamental unit of analysis given that it describes the multivariate and complex covariance of traits within populations (Steppan, Phillips, & Houle, 2002). Lande (1979) demonstrated that the ability to estimate the additive G-matrix allows one to predict how a set of intercorrelated quantitative traits will evolve under genetic drift or in response to selection (Lande & Arnold, 1983). Some traits are likely to be more intercorrelated than others, thus providing a mechanism for understanding how and why some traits are more constrained evolutionarily than others, given complex covariation patterns (e.g., Cheverud, 1984, 1996). In circumstances where good genealogical information is available it is possible to estimate the G-matrix directly from phenotypic characters but in many cases it is necessary to use the phenotypic V/CV matrix (termed the P-matrix) as a proxy for the G-matrix. In cases where both G- and P-matrices can be estimated directly it has been shown that they are proportional across a diverse range of organisms (e.g., Arnold & Phillips, 1999; Cheverud, 1988, 1995, 1996; Konigsberg & Ousley, 1995; Marroig & Cheverud, 2001; Roff, 1996; Steppan, 1997), which lends support to the use of the P-matrix as a substitute for the G-matrix in cases where G cannot be estimated independently.
Bioarchaeologists have long made use of multivariate skeletal datasets to perform biodistance analyses (e.g., Larsen, 2015) whereby the average position of an archaeological sample in comparative morphospace can be estimated, even when sample sizes are small. However, some measures of biological distance, such as Mahalanobis’ distance (Mahalanobis, 1936) require stable estimates of within-group covariation (P-matrix) (Jantz & Owsley, 2001), which necessarily rely on having relatively large population sample sizes. Moreover, the application of more complex evolutionary quantitative genetic methods to test for the past effects of genetic drift and natural selection (e.g., Ackermann & Cheverud, 2002, 2004; Lande, 1977, 1979, 1980a; Lande & Arnold, 1983; Marroig & Cheverud, 2004; Schroeder, Roseman, Cheverud, & Ackermann, 2014; Weaver, Roseman, & Stringer, 2007) are predicated on having stable estimates of population phenotypic covariance, which are rarely available for very fragmentary or small bioarchaeological samples.
In paleoanthropological contexts the problem of small sample size is overcome by using V/CV parameters derived from appropriate extant primate taxa (e.g., Ackermann, 2002; Ackermann & Cheverud, 2004; Harvati, 2003; Harvati, Frost, & McNulty, 2004; Schroeder et al., 2014). For example, Harvati (2003) used both modern human and chimpanzee cranial data as models for patterns of intra- and interspecific morphological variation against which to compare the levels of variation seen amongst Neanderthals and anatomically modern humans. Ackermann & Cheverud (2004) used modern humans, chimpanzees, and gorilla V/CV estimates as extant models for assessing hypotheses of drift and selection as explanatory mechanisms for generating the morphological divergence observed among several australopithecine and genus Homo paleospecies. Recently, Schroeder et al. (2014) used a similar approach when evaluating the likely role of the paleospecies Australopithecus sediba in the evolutionary transition from the australopithecines to the genus Homo.
Here we propose that the same logic be applied in bioarchaeological cases, whereby extant human population covariance parameters be substituted in the case of prehistoric populations (see also Jantz & Owsley, 2001). However, in order to apply this logic it must first be ascertained whether human populations display the same (or very similar) covariance structures or whether globally-distributed populations differ in their covariance structure (Uytterschaut & Wilmink, 1983; González-José, Van der Molen, González-Pérez, & Hernández, 2004). If human populations are largely equivalent in terms of their covariance structure then a global (pooled) covariance matrix could be applied in bioarchaeological contexts. However, if groups differ in fundamental covariance structure then specific geographically or phylogenetically relevant population parameters may be required. González-José et al. (2004) conducted an analysis designed to test whether craniometric correlation and covariance matrices based on 47 cranial traits were consistent among 28 globally distributed populations. They found matched neutral genetic and craniometric distance matrices to be highly correlated (see also Harvati & Weaver, 2006; Roseman, 2004; Smith, 2009; von Cramon-Taubadel, 2009, 2011), which is consistent with a largely neutral microevolutionary model of diversification for the modern human cranium (e.g., Relethford, 1994, 2004; von Cramon-Taubadel, 2014). Using a modification of the random skewers method (Cheverud, 1996), González-José et al. (2004) found all population samples to exhibit significantly (p < .01) similar (r ∼ 0.73) covariance matrices, which they interpret as representing a common and stable V/CV pattern across all human groups. However, this study did not tease apart more specific aspects of among-population shared V/CV patterns and while correlation coefficients were found to be reasonably high (r = 0.61–0.82), similar analyses across different species and genera of platyrrhine primates (Marroig & Cheverud, 2001) yielded comparable (if not higher) covariance matrix similarity coefficients (average, r = 0.80), even after adjusting for imperfect matrix repeatabilities. As a point of comparison, Ackermann (2002) found adjusted correlation coefficients of between 0.73 and 0.89 for the cranial covariance similarities among hominoid species (humans, chimpanzees, bonobos, and gorillas). Interestingly, González-José et al. (2004) interpreted their modern human results as suggesting that human cranial covariance is stable and strongly associated like the platyrrhines considered by Marroig & Cheverud (2001), as opposed to the very different covariance patterns observed among hominoids by Ackermann (2002), despite the similar correlation coefficients yielded by all these studies. This interpretation highlights the fact that simply finding relatively highly correlated and significantly similar V/CV matrices is not sufficient to conclude that they are “equivalent” in terms of their overall structure or their evolutionary potential to respond to selection.
Part of the reason for this confusion is because covariance matrices can, due to their multivariate nature, vary structurally in a number of different ways (see e.g., Phillips & Arnold, 1999; Steppan et al., 2002). For instance, two covariance matrices could be proportional but not equal, meaning that they have the same structure but each element of the matrix is multiplied by some constant, i.e., the matrices share identical eigenvectors or principal components, but differ in their eigenvalues by some proportional amount. Alternatively, two matrices could share the same principal component structure but the eigenvalues in each case could differ (referred to as the common principal components [CPC] model). Matrices could be completely unrelated meaning they share no common principal components at all, or they may share only a proportion of their CPCs with the total number of possible individual CPCs being equal to the numbers of traits minus one.
The goal of this article is to compare modern human cranial V/CV matrices to assess their structural similarities and differences systematically. This research forms a preliminary step within a larger research program designed to decipher whether differences in phenotypic covariance exist among human populations, and what the implications of any potential differences are for the evolutionary analyses of prehistoric human groups. Given the potential complexity of V/CV matrix similarity and difference, we apply two different but complementary methods; one that compares the strength of correlated responses to simulated selection vectors (“random skewers”) and another that uses a hierarchical approach to test the structural equivalence and proportionality of covariance matrices (Flury, 1988) based on the CPC model (Phillips & Arnold, 1999). We test for the equivalence of human craniometric V/CV matrices using the well-known global craniometric database compiled by William Howells (Howells, 1973, 1996). We assess the equivalence of V/CV matrices for both form (shape and size) and shape (adjusted for isometric scaling) data. All tests were carried out using all population samples (global analysis), on a pairwise population sample basis, and by comparing each population against a global matrix based on all other population samples (jackknife routine).
Finally, we test whether potential variation among individual population sample covariance matrices can be explained by such factors as sample size, geographic region, average cranial size, average divergence of population samples from the mean cranial form/shape, and the pairwise craniometric distances between all populations. Previous studies using the random skewers and the CPC model (see details below) found that sample size can affect the results in significant ways (e.g., Steppan, 1997; Cheverud & Marroig, 2007; Buehler, Versteegh, Matson, & Tieleman, 2011). In addition, González-José et al. (2004) suggested that some differences in among-population sample covariance structure may be geographically related (see also Uytterschaut & Wilmink, 1983), with South Asian populations displaying generally lower among-group similarity than observed among samples from other geographic regions. They also suggested that isolated or very variable populations (possibly due to admixture/gene flow) may differ in terms of their covariance structures in systematic ways. Therefore, we explore the potential effects of geography, population dispersion, and population history on patterns of among-population cranial covariance structure.
2 Materials and methods
2.1 Materials: Dataset
Craniometric data were collated from the freely available W.W. Howells database (Howells, 1973, 1996), which comprises 57 cranial measurements for 30 globally distributed population samples (Table 1). It should be acknowledged that the Howells’ dataset may not be free of sampling biases, as certain geographic regions are more extensively sampled than others, and some degree of cranial selection may have occurred, which could artificially deflate the phenotypic variance of certain population samples. Nevertheless, the Howells’ database represents one of the most comprehensive global craniometric datasets available, and the measurement system used by Howells is routinely applied in bioarchaeological contexts. All of the populations sampled by Howells include male but not necessarily female specimens. Therefore, in order to maximize the number of population samples considered in our analysis, and to control for the potentially confounding effects of sexual dimorphism, only male specimen data were used. Sample sizes varied from 29 to 57 male specimens per population. The database also includes two small samples (n = 10 each) of Maori (North and South). These groups were included in the analyses in order to test the effects of including numerically small samples as might be typical in bioarchaeological datasets. Population samples were also grouped according to broad geographic region (Table 1). Given that the aims of this study are to ascertain the reliability of using extant global estimates of craniometric covariance structure in bioarchaeological contexts, we chose to use only 14 cranial measurements that are generally obtainable from even fragmentary or poorly preserved archaeological material (e.g., von Cramon-Taubadel & Pinhasi, 2011; Brewster, Meiklejohn, von Cramon-Taubadel, & Pinhasi, 2014). This reduced set of cranial traits reflects more accurately the reality of bioarchaeological datasets in terms of numbers of variables, while still capturing the major aspects of overall cranial shape and size variation (Table 2). Both the “raw” (i.e., form) data and size-adjusted data were analyzed. Adjustment for isometric scaling was achieved by dividing each measurement by the geometric mean of all measurements for that individual (Darroch & Mosimann, 1985; Jungers, Falsetti, & Wall, 1995).
| GeoRegion | Population | Sample size |
|---|---|---|
| Africa | Teita | 33 |
| Egypt | 58 | |
| Zulu | 55 | |
| San | 41 | |
| Dogon | 47 | |
| Europe | Zalavar | 53 |
| Berg | 56 | |
| Norse | 55 | |
| Asia | Andaman | 35 |
| Buriat | 55 | |
| Hainan | 45 | |
| Anyang | 42 | |
| Philippines | 50 | |
| Atayal | 29 | |
| South Japan | 50 | |
| North Japan | 55 | |
| Ainu | 48 | |
| Americas | Santa Cruz | 51 |
| Arikara | 42 | |
| Peru | 55 | |
| Inugsuk | 53 | |
| Oceania | Guam | 30 |
| Australia | 52 | |
| Tolai | 56 | |
| Tasmania | 45 | |
| Mokapu | 51 | |
| Moriori | 57 | |
| Easter Island | 49 | |
| Maori (North) | 10 | |
| Maori (South) | 10 |
| Code | Measurement description |
|---|---|
| GOL | Glabello-Occipital length (max cranial length) |
| BNL | Basion-Nasion length (upper facial projection) |
| BBH | Basion-Bregma height (max cranial height) |
| XCB | Maximum cranial breadth |
| XFB | Maximum frontal breadth |
| ZYB | Bizygomatic breadth |
| AUB | Biauricular breadth |
| ASB | Biasterionic breadth |
| BPL | Basion-Prosthion length (lower facial projection) |
| NPH | Nasion-Prosthion height (facial height) |
| NLH | Nasal height |
| NLB | Nasal breadth |
| OBH | Orbital height |
| OBB | Orbital breadth |
2.2 Methods
The form and shape datasets were subject to an R-matrix analysis (Relethford & Blangero, 1990) under assumptions of complete heritability (h2 = 1) in RMET 5.0 in order to generate pairwise population craniometric distance matrices (D2-matrices) and the diagonal elements of the resultant R-matrix (Rii) for each population sample. This latter measure provides an estimate of how divergent any particular sample is in terms of average morphology relative to all other population samples included in the dataset. Covariance matrices based on the form and shape datasets were calculated for each population sample and for the total global dataset assuming no population substructure. In order to perform the jackknife routine, iterative versions of the global covariance matrix were calculated whereby each population sample was individually removed in turn to create a jackknifed version of the global matrix against which each population sample could be compared.
2.2.1 Random skewers
The “random skewers” method (Cheverud, 1996) for assessing the equivalence of covariance matrices operates on the principle of subjecting two or more covariance matrices to a large number (>1,000) of random selection vectors and then measuring the extent to which their multivariate responses to selection (Lande, 1979) are correlated. Selection vectors are randomly drawn (hence the name “random skewers”) from a uniform distribution ranging from 0 to 1 and randomly assigned positive or negative signs with a probability of 0.5 (Cheverud & Marroig, 2007). In essence, the method works by applying the same simulated multivariate selection pressures to two matrices and assessing the extent to which their simulated responses are correlated. If two matrices have the same or very similar covariance structures, the average response is expected to be co-linear (r ∼ 1.0), while if two covariance matrices are completely unrelated, the average response will be equal to or close to zero (r = 0.0).
Random skewers analyses were performed in R 3.2.2. using the evolqg package, the RandomSkewers function, and applying 1,000 random selection vectors. Results were generated on a pairwise population basis for both form and shape as well as for each population sample compared against the jackknifed global matrices. The pairwise sample-values were correlated against the craniometric distance matrix using a Mantel (1967) matrix correlation test to assess whether more closely related populations tended to share more highly correlated responses to selection. Finally, the resultant r values from the jackknife analysis were examined in light of such possible explanatory factors as sample size, cranial size (geometric mean of all measurements), average population divergence (i.e., Rii), and geographic region.
2.2.2 Common principal components method
While the random skewers method provides a measure of the equivalence of covariance matrices in terms of their simulated evolutionary responses to hypothetical selection pressures, it cannot be used to ascertain the equivalence of covariance matrices at all possible levels of structure. Therefore, we also performed a common principal components (CPC) analysis, which allows for the testing of multiple hypotheses of equivalence among covariance matrices in a hierarchical fashion (Ackermann, 2002; Arnold & Phillips, 1999; Ackermann & Cheverud, 2000; Cheverud & Marroig, 2007; Flury, 1987, 1988; Phillips & Arnold, 1999; Steppan, 1997). Based on Flury's (1987, 1988) hierarchical model, the method allows for more complex associations between covariance matrices to be assessed, beyond gross judgments of being equal or not. Common principal components (CPC) are extracted based on a decomposition of covariance matrices into eigenvalues and eigenvectors, and then the hierarchical assessment of similarity between matrices proceeds from unrelated structure to a common first principal component (CPC1), common CPC1 and CPC2, first three CPCs in common, etc., through to all CPCs being shared in common, proportionality of matrices, and finally equality of matrices (Ackermann, 2002). Proportionality implies that matrices have identical eigenvectors but differ in their eigenvalues by some constant. Full CPC implies that matrices share principal component structure (eigenvectors) but eigenvalues associated with individual CPCs differ. Alternatively some matrices may only share a proportion of their CPC structure from CPC1 through to CPC(r − 2), where r equals the number of traits used to construct the covariance matrices (Phillips & Arnold, 1999).
Two measures of matrix similarity were employed, which we identify as “hypothesis-testing” and “lowest AIC” (or “model-fitting”) approaches. Hypothesis testing is based on a hierarchical (step-up) model building comparison, whereby the significance of each level is compared against the next level in the hierarchy. For example, if two matrices are proportional, they must by definition also share a full CPC structure or if they share 10 CPCs they must also share 9 CPCs etc. The likelihood that a particular hypothesis is true is determined by the extent of difference between the original matrix and a constrained matrix, constructed using maximum likelihood such that the hypothesis being tested (equality, proportionality etc.) is true. Significance is assessed using a standard χ2 test of this difference, whereby the lower model in the hierarchy is compared against the next highest model in the hierarchy (termed the “step-up” approach; Flury, 1988; Phillips & Arnold, 1999). Reading the hierarchy from the bottom up (i.e., from unrelated structure, through the CPCs, to matrix equality), a significant p value indicates that the lower model in that case provides a better description of the data (Buehler et al., 2011). While the hypothesis-testing approach has the advantage of assigning a specific test of significance, it has been argued that a model-fitting approach may be more appropriate than simply comparing alternative hypotheses in a hierarchical fashion (Ackermann, 2002; Ackermann & Cheverud, 2000; Arnold & Phillips, 1999; Flury, 1988; Phillips & Arnold, 1999). Thus, we also identified the model in the hierarchy with the lowest Akaike information criterion (AIC), a statistic that balances the number of model parameters estimated with the size of the log-likelihood function (see Steppan, 1997), as indicative of the best-fitting model of covariance similarity for each comparison.
CPC analyses were performed in the software program “CPC” (Phillips, 1998) available from Patrick Phillips, which performs the hierarchical analyses outlined by Flury (1988). Results were generated on a pairwise population sample basis for both form and shape, for the entire global dataset, as well as for each population sample compared against the jackknifed global matrix. Results for the hypothesis-testing and model-fitting approach (lowest AIC) for the jackknife analysis and for the pairwise-population analyses were numerically coded (1 = equality, 2 = proportionality, 3 = Full CPC, 4 = 12 CPCs, 5 = 11 CPCs … 16 = unrelated) such that they could be statistically compared against such possible explanatory factors as sample size, cranial size (geometric mean of all measurements), population divergence (Rii), and geographic region. Finally, the pairwise-population sample coded matrices were correlated against the craniometric distance matrix using a Mantel (1967) matrix correlation test to assess whether more closely related population samples tend to share more similar hypotheses of covariance similarity and best-fit models of equivalence than samples from populations not thought to be closely related.
3 Results
Figure 1 shows plots of the first two principal co-ordinate axes representing the shape and form datasets, with over 50% of the total morphological variance represented in each case. Colored polygons delineate the major geographic regions indicated in Table 1 and verify the geographic structure known to exist in modern human cranial datasets (e.g., Howells, 1973; Relethford, 1994, 2001, 2004), which is consistent with a largely neutral model of microevolutionary differentiation (e.g., Betti, Balloux, Amos, Hanihara, & Manica, 2009; Harvati & Weaver, 2006; Roseman, 2004; Roseman & Weaver, 2004; Strauss & Hubbe, 2010; von Cramon-Taubadel, 2009, 2011, 2014).
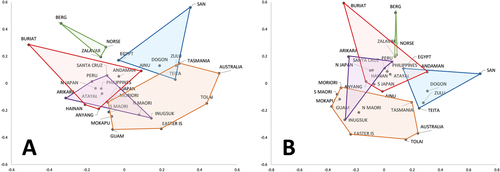
Plots of the first two principal co-ordinate axes for the analysis of shape (A) and form (B), representing over 50% of the total variance in each case. Colored polygons represent major geographic regions as shown in Table 1. A. PCo1 (x-axis) = 27.3%, Pco2 (y-axis) = 24%. B. PCo1 = 27.6%, PCo2 = 24.4% of total variance.
3.1 Random skewers
The results of the random skewers (RS) analyses indicate that all population samples share significant (p < .01) and relatively strong correlated responses to selection (see Supporting Information Tables A (form) and B (shape)). R values for pairwise population sample RS comparisons ranged from r = 0.9296 (N Japan-S Japan) to r = 0.4899 (S Maori-N Maori) for form data, and from r = 0.9218 (San-Egypt) to r = 0.5229 (S Maori-Easter Island) for shape data. Table 3 presents the results for the jackknifed RS analyses ordered from the highest to the lowest r values for the form data. In both the form and the shape datasets, the two numerically small (n = 10) Maori samples had the lowest jackknifed RS r values of all the population samples considered.
| Form | Shape | |||||
|---|---|---|---|---|---|---|
| Population | RS r value | p | St Dev | RS r value | p | St Dev |
| S Japan | 0.947 | <.001 | 0.048 | 0.906 | <.001 | 0.062 |
| Easter Island | 0.939 | <.001 | 0.047 | 0.929 | <.001 | 0.046 |
| Peru | 0.925 | <.001 | 0.063 | 0.891 | <.001 | 0.058 |
| Zalavar | 0.925 | <.001 | 0.060 | 0.927 | <.001 | 0.044 |
| Santa Cruz | 0.924 | <.001 | 0.067 | 0.892 | <.001 | 0.069 |
| Moriori | 0.919 | <.001 | 0.066 | 0.869 | <.001 | 0.076 |
| Philippines | 0.917 | <.001 | 0.087 | 0.890 | <.001 | 0.067 |
| Mokapu | 0.914 | <.001 | 0.090 | 0.912 | <.001 | 0.057 |
| Arikara | 0.913 | <.001 | 0.080 | 0.895 | <.001 | 0.067 |
| N Japan | 0.906 | <.001 | 0.072 | 0.909 | <.001 | 0.057 |
| Hainan | 0.901 | <.001 | 0.094 | 0.910 | <.001 | 0.066 |
| Atayal | 0.901 | <.001 | 0.104 | 0.843 | <.001 | 0.114 |
| San | 0.898 | <.001 | 0.096 | 0.869 | <.001 | 0.073 |
| Buriat | 0.897 | <.001 | 0.083 | 0.885 | <.001 | 0.059 |
| Ainu | 0.894 | <.001 | 0.090 | 0.835 | <.001 | 0.078 |
| Inugsuk | 0.891 | <.001 | 0.084 | 0.877 | <.001 | 0.071 |
| Tolai | 0.889 | <.001 | 0.093 | 0.883 | <.001 | 0.068 |
| Tasmania | 0.889 | <.001 | 0.087 | 0.823 | <.001 | 0.097 |
| Berg | 0.886 | <.001 | 0.091 | 0.891 | <.001 | 0.064 |
| Zulu | 0.885 | <.001 | 0.101 | 0.860 | <.001 | 0.092 |
| Norse | 0.884 | <.001 | 0.087 | 0.836 | <.001 | 0.095 |
| Anyang | 0.878 | <.001 | 0.092 | 0.882 | <.001 | 0.078 |
| Guam | 0.875 | <.001 | 0.108 | 0.855 | <.001 | 0.091 |
| Egypt | 0.869 | <.001 | 0.115 | 0.867 | <.001 | 0.073 |
| Australia | 0.868 | <.001 | 0.110 | 0.844 | <.001 | 0.086 |
| Teita | 0.866 | <.001 | 0.109 | 0.809 | <.001 | 0.113 |
| Dogon | 0.865 | <.001 | 0.091 | 0.852 | <.001 | 0.079 |
| Andaman | 0.848 | <.001 | 0.119 | 0.827 | <.001 | 0.089 |
| Maori (South) | 0.728 | .002 | 0.217 | 0.559 | .011 | 0.166 |
| Maori (North) | 0.648 | .006 | 0.185 | 0.718 | .001 | 0.153 |
- St Dev = standard deviation.
- Note. Populations are ordered according to the strength of the correlation (RS r value) between their response to random selection vectors and the response of the global covariance matrix (excluding that particular population) to the same random selection vectors when form V/CV matrices were used.
Table 4 shows the results of the comparison between the RS jackknifed r values and the potential explanatory factors outlined above. The form and shape datasets were highly correlated in terms of their overall RS results (see also Table 3). Of the explanatory factors tested, the only one that had a significant impact on the RS results was sample size, which explained approximately 60% of the variation in RS r values for both the form and shape datasets (Figure 2). When all population samples greater than n = 30 were considered, there was no significant relationship between RS r value variation and sample size, suggesting that sample sizes ≥30 are sufficient for generating stable estimates of population covariance structure based on the 14 cranial variables considered here.
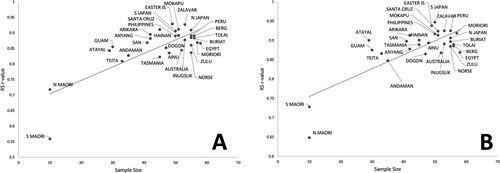
Bivariate plots of Random Skewer (RS) correlation coefficients (jackknifed comparison) against sample size for the shape (A) and form (B) datasets. Sample size explains approximately 60% of the total variance in RS r values in each case.
| Form RS correlation | Shape RS correlation | |||
|---|---|---|---|---|
| Factor | r value | p | r value | p |
| Form RS vs. Shape RS | 0.838 | <.001 | — | — |
| Sample size (All) | 0.771 | <.001 | 0.773 | <.001 |
| Sample size (N > 30) | 0.316 | .116 | 0.385 | .052 |
| Sample size (N > 50) | −0.512 | .052 | −0.349 | .185 |
| Cranial size (geomean) | −0.050 | .794 | −0.068 | .722 |
| Average divergence (Rii) | 0.110 | .564 | 0.199 | .291 |
- Note. Significant results (α = 0.05) in bold.
Mantel tests revealed that there was no significant relationship between pairwise population sample RS r values and craniometric distance for either form (r = −0.128, p = .227) or shape (r = −0.025, p = .819). Similarly, Kruskal-Wallis tests revealed no significant differences among geographic regions in terms of average RS correlations for either form (χ2 = 6.501, df = 4, p = .165) or shape (χ2 = 4.783, df = 4, p = .310). These results indicate that, beyond variation in RS r values generated by including populations represented by very small sample sizes, there is no additional variation that can be explained by the population history or geographic structure of the global samples considered here.
3.2 Common principal components
Table 5 reports the results of the common principal components (CPC) hierarchical analysis of covariance matrix equivalence for all of the population samples considered simultaneously. The two Maori population samples could not be included in the CPC analyses as their small sizes (n = 10) prevented the program from returning legitimate results due to zero or negative eigenvalues. In the case of the hypothesis-testing approach, for both the form and shape data, it was found that a hypothesis of unrelated structure best represented the data, suggesting that at least some of the population matrices differ substantially from one another in terms of their covariance structure. However, the model-fitting approach based on the lowest AIC criterion suggested that a model of proportionality was the best fit to the dataset overall.
| Model | Form | Shape | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Higher | Lower | χ2 | df | p | χ2/df | AIC | χ2 | df | p | χ2/df | AIC |
| Equality | Proportionality | 140.14 | 27 | <.001 | 5.19 | 3,859 | 236.96 | 27 | <.001 | 8.78 | 5,097 |
| Proportionality | Full CPC | 527.78 | 351 | <.001 | 1.50 | 3,772 | 648.07 | 351 | <.001 | 1.85 | 4,914 |
| Full CPC | CPC(12) | 29.25 | 27 | .349 | 1.08 | 3,947 | 58.61 | 27 | <.001 | 2.17 | 4,968 |
| CPC(12) | CPC(11) | 53.71 | 54 | .486 | 1.00 | 3,971 | 113.16 | 54 | <.001 | 2.10 | 4,963 |
| CPC(11) | CPC(10) | 99.65 | 81 | .078 | 1.23 | 4,026 | 192.43 | 81 | <.001 | 2.38 | 4,958 |
| CPC(10) | CPC(9) | 115.46 | 108 | .294 | 1.07 | 4,088 | 124.59 | 108 | .131 | 1.15 | 4,928 |
| CPC(9) | CPC(8) | 165.51 | 135 | .038 | 1.23 | 4,189 | 256.99 | 135 | <.001 | 1.90 | 5,019 |
| CPC(8) | CPC(7) | 199.41 | 162 | .024 | 1.23 | 4,293 | 240.03 | 162 | <.001 | 1.48 | 5,032 |
| CPC(7) | CPC(6) | 286.39 | 189 | <.001 | 1.52 | 4,418 | 269.65 | 189 | <.001 | 1.43 | 5,116 |
| CPC(6) | CPC(5) | 268.54 | 216 | .009 | 1.24 | 4,509 | 337.35 | 216 | <.001 | 1.56 | 5,224 |
| CPC(5) | CPC(4) | 279.43 | 243 | .054 | 1.15 | 4,673 | 423.29 | 243 | <.001 | 1.74 | 5,319 |
| CPC(4) | CPC(3) | 335.37 | 270 | .004 | 1.24 | 4,879 | 487.96 | 270 | <.001 | 1.81 | 5,382 |
| CPC(3) | CPC(2) | 405.48 | 297 | <.001 | 1.37 | 5,084 | 545.39 | 297 | <.001 | 1.84 | 5,434 |
| CPC(2) | CPC(1) | 456.29 | 324 | <.001 | 1.41 | 5,272 | 451.36 | 324 | <.001 | 1.39 | 5,482 |
| CPC(1) | Unrelated | 496.65 | 351 | ≤.001 | 1.42 | 5,464 | 711.54 | 351 | ≤.001 | 2.03 | 5,679 |
| Unrelated | — | 5,670 | 5,670 | ||||||||
- Note. The CPC level at which population equivalence cannot be rejected (α = 0.01) is highlighted in bold underline, while the best AIC solution for comparisons of all covariance matrices is highlighted in bold italics.
Table 6 presents an overview of the results obtained from the jackknifed CPC analyses for both the hypothesis-testing and the model-fitting approaches. As was the case for the global analysis, the hypothesis-testing approach tended to suggest that individual population covariance matrices differ markedly from the global covariance matrix, being in many cases unrelated or only sharing a small proportion of CPCs. In contrast, the AIC criterion tends to suggest a much higher degree of similarity between individual samples and the global matrices, with models of proportionality or shared full CPC structure being supported in many cases. In general, the form results tended to suggest a greater similarity between population-specific covariances and the global covariance matrix than the shape data. Using the coded CPC hypothesis-testing data the form mean rank was 12.74 and the shape mean rank was 15.56, but this difference was not statistically significant (U = 307.5, Z = −1.666, p = .094). In the case of the AIC criterion, the form mean rank was 12.01, while the shape mean rank was 16.49 and this difference was found to be statistically significant (U = 266.5, Z = −2.143, p = .036). The same basic pattern was found for the pairwise population sample comparisons (see Supporting Information Tables C and D), whereby the AIC criterion tended to suggest much more similar V/CV structure among the samples overall relative to the hypothesis-testing approach.
| Form | Shape | |||
|---|---|---|---|---|
| Population | Hypothesis testing | Lowest AIC | Hypothesis testing | Lowest AIC |
| Ainu | Unrelated | Full CPC | Unrelated | Full CPC |
| Andaman | Unrelated | CPC(8) | CPC(2) | CPC(7) |
| Anyang | Unrelated | CPC(11) | Unrelated | Proportionality |
| Arikara | Unrelated | Full CPC | Unrelated | Full CPC |
| Atayal | CPC(1) | Proportionality | Unrelated | Proportionality |
| Australia | Unrelated | CPC(11) | Unrelated | CPC(10) |
| Berg | Unrelated | Full CPC | Unrelated | Proportionality |
| Buriat | Unrelated | CPC(12) | Unrelated | Full CPC |
| Dogon | CPC(1) | Full CPC | Unrelated | CPC(5) |
| Easter Is | CPC(3) | Proportionality | Unrelated | Proportionality |
| Egypt | Unrelated | Full CPC | CPC(4) | CPC(11) |
| Guam | CPC(1) | CPC(12) | Unrelated | Full CPC |
| Hainan | Unrelated | Full CPC | CPC(1) | Proportionality |
| Inugsuk | CPC(2) | Full CPC | CPC(1) | CPC(1) |
| Mokapu | Unrelated | Full CPC | Unrelated | CPC(12) |
| Moriori | CPC(1) | CPC(11) | Unrelated | CPC(11) |
| N Japan | CPC(3) | Full CPC | Unrelated | CPC(12) |
| Norse | CPC(1) | CPC(11) | Unrelated | CPC(11) |
| Peru | CPC(3) | Full CPC | Unrelated | CPC(9) |
| Philippines | Unrelated | Proportionality | CPC(3) | CPC(9) |
| San | Unrelated | Proportionality | Unrelated | CPC(7) |
| Santa Cruz | Unrelated | Full CPC | Unrelated | CPC(10) |
| S Japan | Full CPC | Full CPC | CPC(1) | Full CPC |
| Tasmania | CPC(1) | Full CPC | Unrelated | CPC(1) |
| Teita | Unrelated | Full CPC | Unrelated | Full CPC |
| Tolai | Unrelated | Full CPC | Unrelated | CPC(11) |
| Zalavar | CPC(3) | Full CPC | Unrelated | Full CPC |
| Zulu | Unrelated | Full CPC | Unrelated | CPC(4) |
- Note. Hypothesis testing refers to the CPC level at which population equivalence cannot be rejected (α = 0.05) while the lowest AIC indicates the best fit model of equivalence for that particular comparison.
Table 7 shows the results for the comparison between the CPC jackknifed results and the potential explanatory factors. The results show that the hierarchical hypothesis-testing and the model-fitting approaches do not give correlated results in terms of which population samples share the greatest similarity in covariance structure with the global matrix. In the case of the form datasets, the CPC results are correlated with the random skewers results, such that population samples with the highest RS correlations with the global matrix also tended to share more common structure with the global matrix using both the hypothesis-testing and the model-fitting approaches. However, this was not the case for the shape data, although the comparison between the RS and CPC results based on AIC criterion approached significance (r = −0.359, p = .060). In contrast with the random skewers results, variation in sample size did not appear to affect the results of the CPC covariance comparisons. In the case of the shape data, there was a relationship between average cranial size and the AIC results, suggesting that populations with larger crania also tended to be more similar to the global covariance matrix. There was a significant relationship between pairwise population craniometric distances and the AIC criterion results for both form (r = 0.255, p = .003) and shape (r = 0.408, p < .0001), suggesting that more cranially similar (i.e., more closely related) populations are also more similar in terms of their shared cranial covariance structure. Kruskal-Wallis tests revealed no significant differences among geographic regions in terms of jackknifed CPC results for either form (hypothesis-testing: χ2 = 2.46, df = 4, p = .652. AIC: χ2 = 2.34, df = 4, p = .674) or shape (hypothesis-testing: χ2 = 5.11, df = 4, p = .277. AIC: χ2 = 7.09, df = 4, p = .131).
| Form | Shape | |||
|---|---|---|---|---|
| Factor | r value | p | r value | p |
| Hypo vs. AIC | 0.116 | .557 | −0.172 | .383 |
| RS correlation | ||||
| Hypo | −0.418 | .027 | −0.047 | .814 |
| AIC | −0.455 | .015 | −0.359 | .060 |
| Sample size | ||||
| Hypo | −0.084 | .067 | −0.013 | .946 |
| AIC | 0.159 | .418 | 0.185 | .346 |
| Cranial size (geomean) | ||||
| Hypo | −0.127 | .518 | 0.254 | .192 |
| AIC | 0.302 | .118 | −0.390 | .040 |
| Average divergence (Rii) | ||||
| Hypo | 0.248 | .203 | 0.160 | .417 |
| AIC | 0.212 | .278 | 0.351 | .067 |
- Hypo = hypothesis testing assessment of CPC results; AIC = lowest AIC estimate of best fit model.
- Note. Significant results (α = 0.05) in bold.
4 Discussion
Overall, the results suggest that modern human cranial covariance matrices are broadly similar but not identical. However, the precise nature of these similarities and differences appears to be contingent upon the method used. The random skewers (RS) results suggest that, barring the inclusion of small sample sizes (i.e., n < 30), overall correlations among population samples, and between population samples and the global mean were relatively high (r > 0.7) for both shape and form. However, even excluding the numerically small Maori populations, the lowest pairwise correlations occur between populations with sample sizes of less than 50 (Form: Teita-Guam; Shape: Tasmania-Guam), indicating that it is prudent to employ sample sizes of at least 50 individuals for generating stable human cranial covariance matrices. Also important to consider is the potential effect of the ratio of the number of traits considered to the number of specimens per population sample. In our study, we limited the dataset to 14 cranial traits as more representative of the type of cranial variable datasets often available to bioarchaeologists. We can compare some of our RS results to those reported by González-José et al. (2004) who used the same population samples (except for the two Maori samples) but who included a greater number of cranial variables (n = 47) and included females, although they corrected for sexual size dimorphism. Their average RS r value was 0.73 (SD = 0.0397), while ours was r = 0.86 (SD = 0.0299) for the form dataset, which is most comparable to the dataset used by González-José et al. (2004). The difference between these results is significant when assessed using an independent samples t-test (p < .001). There are only two possible explanations for this difference; either there is an effect of sexual shape dimorphism on the structure of the covariance matrices, or including a larger number of variables relative to average sample size decreases the overall similarity among matrices. Whatever the correct explanation may be, this comparison underlines the fact that the r values from different studies using the RS method cannot be compared directly without controlling for issues such as sample size, number of traits, and sample composition. In sum, of all the potential explanatory factors tested, the only one that affected the RS results in any significant way was sample size. This effect has been noted in previous studies (e.g., Ackermann, 2002; Cheverud & Marroig, 2007). For example, Ackermann (2002) found the lowest RS comparisons associated with their bonobo (Pan paniscus) sample, which consisted of only 21 individuals.
The results from the common principal components (CPC) analyses differed somewhat from the results obtained with random skewers (RS) results, and diverse results were suggested by the hypothesis-testing and the model-fitting (lowest AIC) approaches. The only cases where the two methods provided correlated results were in the case of jackknifed comparisons where the RS results showed the same pattern of results as both CPC approaches for the form dataset. In the case of the shape data, there was a correlation between the RS and the CPC results based on the AIC criterion, but this was only significant at the α = 0.1 level. This lack of synchrony among the different methods has also been noted previously (Ackermann, 2002; Ackermann & Cheverud, 2000; Buehler et al., 2011; Houle, Mezey, & Galpern, 2002; Cheverud & Marroig, 2007; Phillips & Arnold, 1999; Steppan, 1997) and lies, to some extent, in the theoretical assumptions underlying the different methods.
The CPC analyses that consider all population samples simultaneously (Table 5) suggest that all global population V/CV matrices are proportional using the model-fitting (lowest AIC) approach, but they are found to be unrelated with the hypothesis-testing results. How can such differences in results be reconciled? Potential problems with the hypothesis-testing approach have been raised previously. For example, Phillips & Arnold (1999) discuss the need to balance between Type I and Type II errors when assessing the significance values within the hierarchy, for such a balance requires assessing when there is sufficient power to reject a particular hypothesis, while not being able to reject a more complex model. Moreover, Flury's (1988) significance tests rely on the fact that the likelihood statistics are actually χ2 distributed, that the degrees of freedom are known, and that the data are approximately multivariately normally distributed. Flury (Flury, 1987, 1988; Phillips & Arnold, 1999) also points out that it is difficult to establish whether the χ2 values generated are in fact independent, which is an assumption underlying the tests of significant differences. This potential lack of independence suggests that a correction, such as a Bonferroni adjustment, may be required to obtain an appropriate α-value against which to assess significance within the hierarchy. So, for example, an appropriate α-value for our analyses may have been α = 0.05/15 = 0.0033, given that there were 15 potentially nonindependent model comparisons made in each of the CPC analyses. While lowering the α-value would not have affected the results of the global CPC hypothesis testing (Table 5), it would have affected many of the jackknifed and pairwise population comparisons by raising the level in the hierarchy where V/CV matrices ought to be deemed equivalent. Thus, a shift in acceptable α-value could have a dramatic impact on the assessment of significance using the CPC hypothesis-testing approach.
Another issue that has been raised is the effect of large sample sizes on the ability to recover shared covariance structure using the hypothesis-testing approach (e.g., Ackermann & Cheverud, 2000; Buehler et al., 2011; Cheverud & Marroig, 2007; Marroig & Cheverud, 2001; Steppan, 1997). Cheverud & Marroig (2007) note that because the CPC model takes sample size into consideration when deriving the χ2 statistics, larger sample sizes increase the power to reject common structure. This is due, in part, to the fact that the CPC method takes the hypothesis of more similar structure as it is null in each case, rather than unrelated structure as is the case with the random skewers method. Cheverud & Marroig (2007) note that, with large sample sizes, one can simultaneously obtain high RS coefficients (r > 0.9), yet recover a CPC hypothesis test result of “unrelated” structure (see also Houle et al., 2002). Therefore, the effect of sample size is in direct opposition to that seen with the random skewers method, where large samples increase the estimation of similarity. The effect of sample size explains the pattern of CPC hypothesis-testing results we obtained for the jackknife routine (Table 6), where hypotheses higher than unrelated structure were difficult to accept. In the case of the jackknifed results, the highest model accepted (α = 0.05) for the form data was shared CPC(3), while for the shape data it was shared CPC(4). These results, and the fact that they differ so markedly from the model-fitting comparisons (based on the AIC criterion), are best explained by the large sample size (n > 1,000) of the pooled global matrix. However, our comparison of population sample size and the jackknifed results (Table 7) did not pick up on this effect because the sample sizes inputted into the correlation were those of the individual samples, which were all relatively small compared to the global jackknifed matrices. Steppan (1997) notes that increasing the number of characters would also have the same effect as increasing sample sizes, in terms of raising the likelihood of incorrectly rejecting similar covariance structure using the CPC method (see also Ackermann & Cheverud, 2000).
Consideration of all of these factors leads us to agree with Flury (1988; see also Ackermann & Cheverud, 2000) that a model-fitting approach (using the lowest AIC) is the more appropriate measure of where in the CPC hierarchy the “true” V/CV matrix similarity lies. Hence, on the basis of our results, we recommend that future studies utilizing the CPC approach focus on the AIC criterion when evaluating where in the hierarchy the similarity between V/CV matrices lies. Looking at the CPC results purely from the model-fitting perspective indicates that human cranial V/CV matrices are at least proportional to one another (global, Table 5) or share a large proportion of their common principal component structure (jackknifed, Table 6). Nevertheless, despite the overall assessment of similarity, some differences in V/CV similarity patterns are evident (Table 6), particularly when using the shape data. However, we were not able to explain the variation in jackknifed results using the AIC criterion by any of the explanatory factors tested, except for a possible relationship between cranial size and shape V/CV matrices, whereby crania of larger average size also tended to be more similar in terms of shared shape covariance structure with the global matrix. This may be indicative of a weak allometric effect, whereby populations with larger crania also tend to be less variable in terms of shape, which in turn makes them more similar in shape covariance to the global average. We found a marginally significant inverse relationship between cranial size and within-group shape variation (r = −0.37, p = .054), which offers some support for this interpretation, although further work is warranted to properly tease out the relationship between cranial size, shape variation, and their effects on covariance structure.
Perhaps the most interesting finding is the positive and significant relationship between cranial distance and V/CV similarity (as measured using the AIC criterion) for both form and shape. This indicates that there is an effect of population history on the pattern of pairwise covariance similarity among population samples at a global level, consistent with the idea that more closely related groups tend to share more similar cranial covariance structure overall (see also Uytterschaut & Wilmink, 1983). Previous studies have also indicated a phylogenetic signal in their pairwise comparisons of covariance matrices between taxa (Ackermann, 2002; Ackermann & Cheverud, 2000; de Oliveira, Porto, & Marroig, 2009; Steppan, 1997). For example, although Steppan (1997) did not find a strong phylogenetic pattern in terms of shared covariance structure at higher taxonomic levels within the genus Phyllotis (leaf-eared mice), he did find the greatest similarities in covariance structure among populations of the same subspecies. However, given the lack of systematic long-term divergence of covariance patterns with phylogenetic distance, he interpreted the results as being consistent with stochastic evolution of covariance patterns (e.g., under a Brownian motion model), rather than being the result of clade-specific selection patterns (see also Riska, 1985). Overall, therefore, some effect of global population history may be present in the patterns of covariance similarity and difference found here, but the effect appears to be relatively small and there is no evidence that it varies in any systematic fashion with respect to geographic region. Also, it is worth reiterating that no signal of population history was detected from the results of the random skewers analysis, which was mainly driven by population sample size. Marroig & Cheverud (2001) also found no relationship between phylogenetic distance and V/CV matrix similarity in their large sample of platyrrhine taxa. They note that the high V/CV matrix correlations (also found here) and the lack of any phylogenetic signal is consistent with Lande's (1980b) mutation-selection balance model, in the sense that phenotypic means can evolve somewhat independently of any correlated changes in the underlying structure of the covariance matrices. A better understanding of geographic patterns of modern human covariance similarity and difference has important implications for tracking the past actions of both random drift and natural selection, as these evolutionary forces could affect phylogenetic divergence of covariance matrices in different ways (Roff, 2000; Steppan et al., 2002). While we currently have a relatively good understanding of the overall neutral divergence of modern human cranial diversity at a global level (von Cramon-Taubadel, 2014), we still do not fully understand the effects of past microevolutionary forces on patterns of within- and among-population covariance structure.
5 Conclusions: Implications for bioarchaeological applications
Modern human cranial covariance patterns are broadly similar to one another but they are not identical. Some of these differences can be accounted for by such statistical parameters as sample size, number of traits considered, and the composition of the samples. Although it has been repeatedly shown that the modern human cranium has evolved under largely neutral conditions, we cannot assume that stochastic divergence among populations did not result in changes in population-level cranial covariance structure. Therefore, some effect of past population history in terms of migration, genetic drift, isolation, and gene flow on global patterns of shared cranial covariance is possible. In addition, if specific populations have been subject to diversifying natural selection for certain aspects of cranial form (Hubbe et al., 2009; von Cramon-Taubadel, 2014; Roseman, 2016), this may impact the internal covariance structure of the divergent population in systematic ways. However, the precise effects of different evolutionary forces on patterns of among-population differences in phenotypic covariance remain to be formally modeled and empirically tested. Nevertheless, on average, population cranial covariance structures are highly correlated, and appear to be largely proportional in structure. Some populations may deviate more from this global structure than others, which could be related to the specific effects of microevolutionary processes on individual groups or reflect sampling biases (i.e. geographic coverage or sample heterogeneity) inherent in the Howells dataset. Therefore, it would be prudent to verify these findings with additional datasets focusing on different population samples and different sets of craniometric traits.
Nevertheless, it should also be emphasized that despite differences in the cranial covariance structures of hominoid taxa (Ackermann, 2002), using these same taxa as extant models for assessing the relative roles of drift and selection among hominin paleospecies produced largely consistent results (see also Schroeder et al., 2014). This indicates that, as long as the extant covariance matrices being compared are mostly similar in structure, choosing one matrix over another as an extant analogue when applying tests of drift and selection will likely lead to equivalent results. Therefore, we advocate using a pooled global human covariance matrix as an extant parameter matrix in any bioarchaeological applications where the effects of drift on population divergence or the potential response to selection are of interest (Ackermann & Cheverud, 2004; Lande, 1979, 1980a; Schroeder et al., 2014; Weaver et al., 2007). In this case, having stable covariance matrices estimated using large sample sizes will be the more important consideration. However, another goal may be to employ an extant human covariance matrix as a substitute for a prehistoric “population,” where only a few specimens are available. In this situation, the available specimens are assumed to represent the “average” for that extinct population. Using an extant covariance matrix would therefore provide a vehicle for including the archaeological sample in a comparative multivariate analysis, such as a canonical variate analysis, or as a means of calculating population biodistance (e.g., Mahalanobis’ distance). In such cases, we recommend testing the effect of using a phylogenetically and/or geographically relevant extant population alongside a global pooled covariance matrix (see also Jantz & Owsley, 2001), as equivalence of covariance structure across all groups in the analysis cannot be assumed a priori.
Acknowledgments
We are grateful to the late William W. Howells for making his cranial data available and to Patrick Phillips for the freely available CPC software program. We thank the editor, associate editor, two anonymous reviewers, and Stephen Lycett for helpful comments on our manuscript.




