Turning the tables of sex distinction in craniofacial identification: Why females possess thicker facial soft tissues than males, not vice versa
Abstract
Males are universally reported to possess larger facial soft-tissue thickness (FSTT) than females, however, this observation oversimplifies the raw data yielding an underpowered assessment of FSTT sex-patterning where: differences are small (η2 < 5%) and inconsistent (females are routinely larger than males at the cheeks). Here we investigate body-size normalized data to assess whether more general and improved understanding of FSTT sex-variation in humans is possible. FSTTs were measured in 52 healthy living Australians aged 18 to 30 years using B-mode ultrasound. Participants' stature and body mass were also measured. Sex differences were calculated before and after normalization by the aforementioned body-composition variables. Methods were repeated in three other independent samples to evaluate reproducibility: 100 American Whites and 60 American Blacks measured by B-mode ultrasound; and 50 Turkish residents measured by regular supine CT. Compared to raw mean differences (F < M, by −6%), females displayed much thicker FSTTs than males when normalized for body mass (F > M, by +16%). Consequently, while the sexes share similar raw values, females possess much larger FSTTs for their relatively lighter bodies. The relative FSTT difference was 2.7× larger than the raw mean difference. Sex differences in FSTT are of larger magnitude and reversed direction in mass normalized data. Contrary to popular thought, females possess much larger FSTTs than males owing to their generically lighter bodies (−18 kg). These data patterns help explain why the pooling of sex-categorized FSTT does not jeopardize the sex-difference—it is encoded more strongly in terms relative to body mass.
1 Introduction
Human sexual dimorphism is a prime focus in physical anthropology, encompassing a broad range of interests from evolution (Darwin, 1874; Frayer & Wolpoff, 1985; Plavcan, 2001) to growth (Bogin, 1999; Krogman, 1972), health (Mayes & Watson, 2004; Riggs, Khosla, & Melton, 2002; Wells, 2007), and forensic science (İşcan & Steyn, 2013; Reichs, 1998; Stewart, 1979). Although some small sexual dimorphisms beyond the genitalia are present at birth, the majority of the sex differences in the adult are the result of growth trajectories that diverge at puberty, and are thus classified as secondary sexual characteristics (Bogin, 1999; Wells, 2007). By the time adulthood is reached—typically at younger chronological ages in females than males (Bogin, 1999)—there exists a broad range of secondary sex differences including those in stature, skeletal robustness, lean body mass, fat mass, fat distribution, and hair patterning, to name just a few (Martin & Saller, 1957; Wells, 2007).
Sex variation of the human face has been of interest to those concerned with facial growth and craniofacial identification ever since the late 1880s (His, 1895; Krogman, 1972; Martin, 1928; Subtelny, 1959; Welcker, 1883). The first study on the sex differences of the facial soft-tissue thicknesses was undertaken in 1895 using needle puncture methods in conjunction with cadavers (His 1895), and reported the now common observation that “female[s]…are everywhere somewhat less than that of men, a behavior that appears due to the thinner skin of the woman” (His, 1895, p. 407). Following repeat studies by Eggeling (1911) and Gerasimov (1955) this observation became regarded as a ground truth in craniofacial identification, and was more recently cemented as fact by statistical significance testing (De Greef, Claes, Vandermeulen, Mollemans, Suetens, & Willems, 2006; Dong et al., 2012; Drgáčová, Dupej, & Velemínská, 2016; Helmer, 1984; Sahni, Singh, Jit, & Singh, 2008; Simpson & Henneberg, 2002; Wang, Zhao, Mi, & Raza, 2016; Wilkinson, 2004).
A limitation of p values, however, is that they communicate nothing about the strength of the effect, which is also important (Cohen, 1990; Kirk, 1996; Wasserstein & Lazar, 2016). Mean data from past studies clearly demonstrate only marginal sex differences on average (Figure 1). The similarities in the thicknesses of the facial soft tissues between males and females are more striking than the differences. Figure 1 also indicates that the relationship of M > F does not hold across the entire face surface; e.g., females typically have larger raw values than males at the cheeks as reported elsewhere (De Greef, Vandermeulen, Claes, Suetens, & Willems, 2009; Stephan & Simpson, 2008; but for deviations across more extensive face regions see: Chan, Listi, & Manhein (2011), El-Mehallawi & Soliman (2001), and Phillips and Smuts (1996)). Consequently, the generalization that males possess larger values than females is not a particularly good one, overstating some relationships and ignoring others.
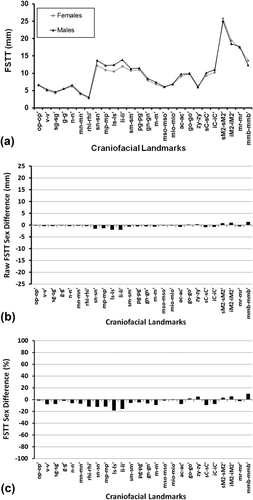
Weighted mean FSTT values by sex for 26 landmarks calculated across 62 studies published between 1883 and 2015 after Stephan and Simpson (2008), showing the very small sex difference in FSTTs (n = 6,786 individuals at pogonion). (a) Line plot modified from “Facial soft tissue depths in craniofacial identification (part I): An analytical review of the published adult data,” by C. N. Stephan and E. K. Simpson, 2008, Journal of Forensic Science, 53, p. 1257, with permission from Wiley. Trend lines have been added to facilitate differentiation of the sex-specific values, but note that they do not represent any time series or sequence order. (b) The raw sex difference magnitudes from (a), Δsex (mm) = x̄females (mm) − x̄males (mm), plotted against a y-axis scale appropriate for the mid-ramus soft-tissue thickness (mr-mr′). (c) The percentage sex differences, calculated by standardizing the sex difference against the mean female value at the same landmark, Δsex (%) = (Δsex (mm)/x̄females (mm)) × 100.
The strength of the sex effect is also unimpressive as measured by η2/r2 values, with sex explaining <5% of the total FSTT variance (Stephan, Norris, & Henneberg et al., 2005; Stephan, Simpson, & Byrd, 2013). This is equivalent to approximately one fifth of the strength of the same variable's effect (25%) on stature (Stephan et al., 2013) or body weight (Henneberg, 1990). With the added consideration of large measurement errors for FSTT data collection, it is of little surprise that the utility of such small FSTT sex differences evaporates in practical craniofacial identification contexts (Stephan, 2015a). For example, sex- and ancestry-specific FSTT means have been shown to often work better as predictors in nonmatched samples, i.e., those of a different sex and ancestry, rather than those samples for which the predictive methods were derived (Stephan, 2015a). Stronger and more robust FSTT predictive models are, therefore, in want for forensic craniofacial identification casework (Stephan, 2015a).
Rather than retaining sex-separated data that display miniscule differences and which are associated with large measurement errors, data amalgamation, or pooling has been advocated to boost sample sizes and increase reliability under The Law of Large Numbers (Stephan, 2014; Stephan et al., 2005, 2013; Stephan, Munn, & Caple, 2015; Stephan & Simpson, 2008). While The Law of Large Numbers is a basic, well-known, and a foundational statistical principle (Moore & McCabe, 2003), its application to sex-categorized FSTTs has been viewed as a major procedural shift and that has slowed uptake. For example, İşcan and Steyn state that data pooling to increase sample size is in “strong contrast to various other studies which demonstrated that [sex] differences exist” (İşcan & Steyn, 2013, p. 370). However, the data could hardly be more numerous and/or compelling—small sex differences are routinely reported by numerous authors in the literature (see for review: Stephan & Simpson, 2008) and with large degrees of the overlap between male and female distributions (Stephan et al., 2005). Together with large measurement errors (noise), this leaves little justification for retaining separate datasets and mandates sex category data pooling (Stephan et al., 2015). The hesitation to embrace this approach, evidenced by continued sex categorization post-2008 (De Greef et al., 2009; Dong et al., 2012; Drgáčová et al., 2016; Hwang et al., 2012; Jia et al., 2016; Wang et al., 2016) is underpinned by an adherence to past-practice for past-practice's sake, succinctly summarized by İşcan and Steyn—“until otherwise proven, it is probably best to still use sex- and population-specific data” (İşcan & Steyn, 2013, p. 371).
A FSTT formulation that extends the benefits of data pooling beyond increased reliability to additionally provide improved accuracy, generality, and biological insight would be ideal. Such a formulation might seem ambitious; however, sex analysis in craniofacial identification has for the past 120 years overlooked one very important factor that might make this formulation possible—data normalization by body scale.
Outside of the craniofacial identification literature it is broadly recognized that differences in body-scale must be considered in sex comparisons because they can act as confounding factors (Huxley, 1932, 1972; Mosimann & James, 1979; Thompson, 1992). That is, if males possess slightly larger raw FSTT at some landmarks because they have generically larger body size than females, then females likely possess much thicker FSTTs relative to males because of their smaller mean body size. The relationship is such that the direction of the currently held sex patterning may reverse (females hold larger FSTTs than males for any given body size) and increase in magnitude.
If this hypothesis holds, then the pooling of the data across the sex categories to increase reliability is incontrovertibly justified because the action does nothing to jeopardize the (relative to body size) sex difference. Indeed, the sex difference in human adult body-scale is well-established in the anthropological literature (Bogin, Wall, MacVean, 1992; Dietz, Marino, Peacock, & Bailey, 1989; Georgi, Schaefer, Wuehi, & Schaerer, 1996; Hamill, Johnson, Reed, & Roche, 1977; Kuczmarski et al., 2002; Little, Galvin, & Mugambi, 1983; Mueller et al., 1980; Roede & van Wieringen, 1985; or see for review: Bogin, 1999; Gripp, Slavotinek, Hall, & Allanson, 2013) and it has additionally been documented within studies of craniofacial identification via co-variance of raw FSTTs with body-mass index (Baillie, Ali Mirijali, Niven, Blyth, & Dias, 2015; Chan et al., 2011; De Greef et al., 2006, 2009; Dong et al., 2012; Jia et al., 2016). Consequently, all the necessary ingredients exist to undertake body-scale normalization of the FSTT data prior to sex comparisons, with the possibility for a win-win solution that simplifies the FSTT data structure on the one hand, whilst simultaneously increasing explanatory power and reliability on the other (Stephan, 2014; Stephan et al., 2005; Stephan & Simpson, 2008).
In this study, we set out to determine what mean sex-pattern (if any) remains when body-scale normalized FSTTs are evaluated in regards to sex, and how these patterns differ from the tiny differences that have been observed for the raw FSTT data.
2 Materials and Methods
We measured FSTTs in 53 healthy living Australians aged 18 to 30 years using B-mode ultrasound, as approved by The University of Queensland's Medical Research Ethics Committee (Approval #2014000740). Gel standoff platforms were employed to mitigate ultrasound transducer pressure on the skin following Stephan & Simpson's (2008) recommendations, thereby minimizing soft-tissue compression during measurement (Figure 2). Facial soft-tissue thicknesses were measured at 14 facial landmarks common to the T-Table as developed by Stephan (2014) and herein described by the updated terminology of Caple & Stephan (2016)—see Table 1 and Figure 3. Participant body height and mass were measured using a stadiometer (Seca® 213, Hamburg, Germany) and digital scales (HoMedics®, Dandenong South, Australia) respectively. Body mass index (BMI) was calculated according to the standard formula of mass divided by height square (kg/m2), with the BMI categories being established in accordance with the sectioning points recommended by the World Health Organization (2015; Figure 4). Due to one outlying BMI result (extremely large BMI far from the distribution cluster at the right most extreme), one subject was excluded from further analysis, so as not to unjustly bias correlations. This resulted in a final tally of 35 female and 17 male subjects (for sample details see Table 2 and Figure 4).
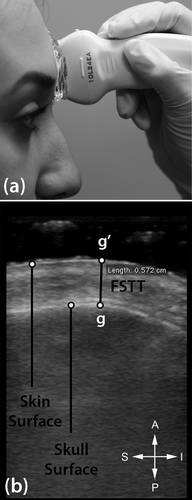
FSTT measurement using B-mode ultrasound: (a) ultrasound transducer with stand-off gel platform at glabella to avoid soft tissue compression at this landmark during measurement (after Stephan and Simpson 2008); and (b) resulting ultrasound image with uncompressed skin surface profile. The image is presented as it comes off the ultrasound machine, so anterior is up and inferior towards the right of the image as marked by the key.
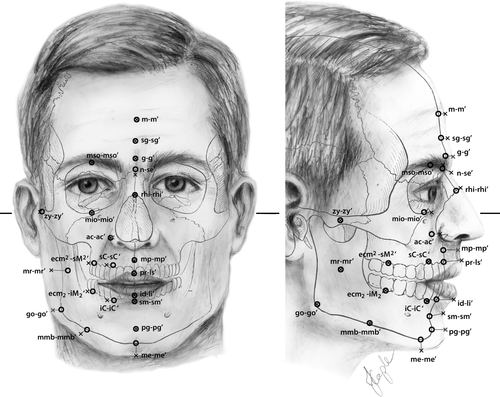
Craniofacial landmark pairs utilized in this study. See Table 1 for definitions. Figure is redrawn after “A standardized nomenclature for craniofacial and facial anthropometry,” by J. Caple & C. N. Stephan, Journal of Legal Medicine, 130, p. 863, with permission from Springer. Bold line indicates the Frankfort horizontal. Crosses represent capulometric (soft tissue) landmarks. Open circles represent craniometric landmarks.
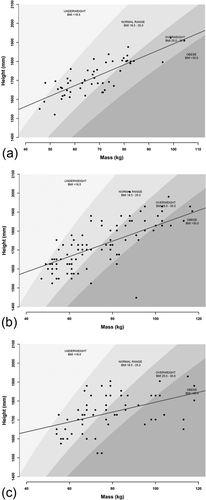
Scatterplots of subjects by height and mass, mapped against BMI classes: (a) This study's sample (Australian Whites); (b) American Whites (Manhein et al., 2000); (c) Americans Blacks (Manhein et al., 2000). The dark gray line represents the Ordinary Least Squares Regression trend line. Underweight BMI domain = light gray shade and BMI increases through to Obese category (dark gray shade) according to World Health Organization sectioning points (World Health Organization, 2015). Plots generated using R code (R Core Team, 2013) available at CRANIOFACIALidentification.com.
| Skeletal landmark | Corresponding paired soft tissue landmark | ||
|---|---|---|---|
| Name (abbr.) | Definition | Name (abbr.) | Definition |
| Metopion (m) | Median point, instrumentally determined on the frontal bone as the greatest elevation from a cord between nasion (see below) and bregma.a | Metopion (mʹ) | Furthest chord length perpendicular to the nasion-bregma chord. a |
| Supra-glabella (sg) | Median point immediately above the forward glabella projection on the smooth upward rising slope of the frontal bone. | Supra-glabella (sgʹ) | Median soft tissue point overlaying sg. |
| Glabella (g) | Most projecting anterior median point on lower edge of the frontal bone, on the brow ridge, in between the superciliary arches and above the nasal root. | Glabella (gʹ) | Most anterior midline point on the forehead, in the region of the superciliary ridges. |
| Nasion (n) | Intersection of the nasofrontal sutures in the median plane. | Sellion (seʹ) | Deepest midline point of the nasofronal angle. |
| Rhinion (rhi) | Most rostral (end) point on the internasal suture. | Rhinion (rhiʹ) | Point overlying rhinion, at the end of the internasal suture, where bone ends and cartilage begins. |
| Mid-philtrum (mp) | Median point midway between subspinale and pr (see below).a | Mid-philtrum (mpʹ) | Point midway between subspinale′ and ls′ (see below), in the median plane. a |
| Prosthion (pr) | Median point between the central incisors on the anterior most margin of the maxillary alveolar rim. | Labiale superius (lsʹ) | Midpoint of the vermilion border of the upper lip (not identical to and not to be confused for Labrale superius). a |
| Infradentale (id) | Median point at the superior tip of the septum between the mandibular central incisors. | Labiale inferius (liʹ) | Midpoint of the vermilion border of the lower lip (identical to labrale inferius). a |
| Supramentale (sm) | Deepest median point in the groove superior to the mental eminence (orthodontic point B). | Supramentale (smʹ) | Deepest midline point of the mentolabial sulcus. |
| Pogonion (pg) | Most anterior median point on the mental eminence of the mandible. | Pogonion (pgʹ) | Most anterior midpoint of the chin, located on the skin surface anterior to the identical bony landmark of the mandible. |
| Menton (me) | Most inferior median point of the mental symphysis (may not be the inferior point on the mandible as the chin is often clefted on the inferior margin). | Menton (meʹ) | Most inferior median point of the chin. |
| Mid-supraorbital (mso) | Point on the anterior aspect of the superior orbital rim, at a line that vertically bisects the orbit. | Mid-supraorbital (msoʹ) | Point anteriorly adjacent to the superior orbital rim, at a line that vertically bisects the orbit. |
| Mid-infraorbital (mio) | Point on the anterior aspect of the inferior orbital rim, at a line that vertically bisects the orbit. | Mid-infraorbital (mioʹ) | Point anteriorly adjacent to the inferior orbital rim, at a line that vertically bisects the orbit. |
| Alare curvature pt. (ac) | Hard tissue approximation of soft tissue acʹ, approximately 5 mm lateral to the alare landmark.a | Alare curvature pt. (acʹ) | The most posterolateral point of the curvature of the base line of each nasal ala. |
| Zygion (zy) | Instrumentally determined as the most lateral point on the zygomatic arch. | Zygion (zyʹ) | Most lateral point overlying each zygomatic arch, identified as the point of maximum bizygomatic breadth of the face. |
| Gonion (go) | Point on the rounded margin of the angle of the mandible, bisecting two lines one following vertical margin of ramus and one following horizontal margin of corpus of mandible. | Gonion (goʹ) | Most lateral point on the mandibular angle, adjacent to go, identified by palpation. |
| Supracanine (sC) | Point on the maxillary alveolar margin centrally above the maxillary canine. | Supracanine (sCʹ) | The soft tissue projection of sC. |
| Infracanine (iC) | Point on the mandibular alveolar margin centrally below the maxillary canine. | Infracanine (iCʹ) | The soft tissue projection of iC. |
| Ectomolares (ecm2 and ecm2) | Most lateral point on the buccal alveolar margin, at the center of the second molar position. Superscript number designates the maxillary landmark; subscript number designates the mandibular landmark. | Supra-2nd-molar (sM2ʹ and iM2ʹ) | Point overlying ecm, the midpoint of the alveolus of the second maxillary molar. |
| Mid-ramus (mr) | Midpoint along the shortest antero-posterior depth of the ramus, in the masseteric fossa, and usually close to the level of the occlusal plane. | Mid-ramus (mrʹ) | Point directly overlying mr, best determined by X-ray but can be extrapolated from surface anatomy features including the masseter muscle mass, the posterior margin of the mandible and the zygomatic arch. |
| Mid-mandibular border (mmb) | Point on the inferior border of the corpus of the mandible midway between pg and go. | Mid-mandibular border (mmbʹ) | Point directly overlying mmb, midway between pg′ and go′. |
- Entries follow the C-Table as far as possible (Stephan and Simpson, 2008), with definitions after Caple and Stephan (2016). Supraglabella (sg-sgʹ), infracanine (iC-iCʹ), and supracanine (sC-sCʹ) represent additions not included by Caple and Stephan (2016). Positions on the skull/face are illustrated in Figure 3.
- a For additional landmarks used to define the 22 designated landmarks of this study (bregma, subspinale etc.) see Caple and Stephan (2016).
| Sample | Author | Sex | n | Age (yrs) | |||
|---|---|---|---|---|---|---|---|
| x̄ | s | min. | max. | ||||
| Australian Whites | This study | M | 17 | 21.6 | 2.5 | 18 | 27 |
| F | 35 | 20.6 | 2.1 | 18 | 25 | ||
| American Blacks | Subset of Manhein et al. (2000) | M | 35 | 20.7 | 3.2 | 18 | 30 |
| F | 25 | 22.5 | 3.8 | 18 | 29 | ||
| American Whites | Subset of Manhein et al. (2000) | M | 43 | 20.2 | 2.5 | 18 | 27 |
| F | 57 | 20.3 | 2.8 | 18 | 28 | ||
| Turks | Subset of Bulut et al. (2014) | M | 25 | 44.1 | 8.2 | 30 | 58 |
| F | 25 | 45.6 | 8.1 | 31 | 58 | ||
Means, shorths (Andrews et al., 1972), and shormaxes (Stephan et al., 2013) were calculated for the sex-separated raw data using TDStats v2013.1 (Stephan, 2014; or see CRANIOFACIALidentification.com for the updated version). Shorths represent the mean of the densest half of the observations making this statistic a useful central tendency indicator for any unimodal dataset, even those that have large skewness (Andrews et al., 1972). Shormaxes represent the 75th percentile between the shorth and the maximum value providing an approximation of the data falling within the right tail (Stephan & Guyomarc'h, 2016; Stephan et al., 2013).
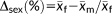 (1)
(1) (2)
(2)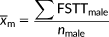 (3)
(3) (4)
(4) (5)
(5)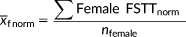 (6)
(6)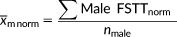 (7)
(7)Methods were repeated for subsamples from three other datasets previously published by two separate groups of authors (Bulut et al. 2014; Manhein et al., 2000). The Manhein et al. (2000) data comprises living subjects measured by B-mode ultrasound in an upright posture, and the Bulut et al. (2014) data concerns living subjects measured by CT in a supine position. Manhein et al. (2000) reported height and body mass variables (for BMI plots see Figure 4) and were drawn from the C-Table repository at CRANIOFACIALidentification.com.
Both American White and Black data of Manhein et al. (2000) were analyzed, but only for individuals aged 18 to 30 years; thereby replicating age ranges for the Australian White sample mentioned earlier. Three individuals for whom mass was not recorded and two additional males with incomplete FSTT data were excluded, yielding final sample sizes of 57 female and 43 male American Whites, and 25 female and 35 male American Blacks. The subset of the Bulut et al. (2014) data used here comprises individuals aged from 30 to 58 years, represented by 25 females and 25 males. Only mass accompanied this subset, so normalization by height and BMI was not possible.
While ancestral group labels are commonly plagued by severe limitations—e.g., oversimplification of continuous range of genetic variation to named groups, misinterpretation of named groups for distinct categories, and group derivation from subjective rather than objective criteria (AAPA, 1996; Gould, 1996; Jorde & Wooding, 2004; Montagu, 1942; Sauer, 1992; Stewart, 1979; Yudell, Roberts, DeSalle, & Tishkoff, 2016)—such ancestry labels have commonly been used in the FSTT literature (see for review: Wilkinson, 2004). While we describe at length elsewhere how ancestral trends in FSTTs are largely overstated due to measurement noise (Stephan, 2014, 2015b; Stephan et al., 2013, 2015; Stephan & Simpson, 2008), that does not excuse some attempt at communicating sample composition herein. Consequently, we use the term “Australian Whites” to denote Australians of self-reported European extraction and use the terms American Whites and Blacks in accordance with the original publishing authors of that work (Manhein et al., 2000). The Turkish sample is simply reported as Turkish to be consistent with the original study from which these data were derived (Bulut et al., 2014).
In addition to mean trends, we also plotted the raw and Log10-transformed data in scatterplots, and used Standard Major Axis regression (Reduced Major Axis Regression) on the Log10 data to explore slopes relative to Huxley's (1932) criteria of α = 1.0 for isometry, α > 1.0 for positive allometry, and α < 1.0 for negative allometry (see Bonduriansky, 2007; Mosimann & James, 1979).
3 Results
Males possessed larger body size than the females for all four datasets (Tables 3-6), being on average 159 mm taller, 18 kg heavier, and two BMI points larger. Mean Pearson Product Moment Correlation Coefficients (r) between FSTT and mass, height and BMI were weak to moderate: 0.23, 0.29, and 0.19, respectively. In terms of raw FSTTs, females held similar (but not the same) values as males: largest Δsex = 3.3 mm at mid-philtrum for American Blacks (Tables 3-6).
| Females (f) | Males (m) | Δsex | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n = 35; age = 18–25 yrs | n = 17; age = 18–27 yrs | ||||||||
| x̄ | s | Shorth | Shormax | x̄ | s | Shorth | Shormax | (x̄m − x̄f) | |
| Height (mm) | 1668 | 57 | – | – | 1817 | 53 | – | – | 149 |
| Mass (kg) | 62 | 8 | – | – | 81 | 13 | – | – | 19 |
| BMI (kg/m2) | 22 | 3 | – | – | 24 | 3 | – | – | 2 |
| Facial soft-tissue thicknesses (mm) | |||||||||
| m-m' | 4.3 | 0.7 | 4.1 | 5.4 | 4.5 | 0.7 | 4.7 | 5.2 | 0.2 |
| g-g' | 5.7 | 0.9 | 5.6 | 6.8 | 5.5 | 0.7 | 5.3 | 6.3 | −0.2 |
| n-se' | 6.9 | 1.2 | 6.8 | 8.1 | 8.0 | 1.0 | 7.6 | 8.9 | 1.1 |
| rhi-rhi' | 2.3 | 0.4 | 2.4 | 2.6 | 2.4 | 0.6 | 2.2 | 3.2 | 0.1 |
| mp-mp' | 10.9 | 1.1 | 10.9 | 12.0 | 12.1 | 1.4 | 12.7 | 13.2 | 1.2 |
| sm-sm' | 11.0 | 1.4 | 10.4 | 12.3 | 11.9 | 1.5 | 12.5 | 13.9 | 0.9 |
| pg-pg' | 8.3 | 1.5 | 8.3 | 9.9 | 9.1 | 1.8 | 8.6 | 11.1 | 0.8 |
| me-me' | 7.1 | 1.3 | 7.3 | 8.1 | 7.9 | 1.4 | 8.5 | 9.4 | 0.8 |
| mso-mso' | 7.6 | 0.9 | 7.7 | 8.8 | 8.2 | 0.7 | 8.0 | 8.9 | 0.6 |
| mio-mio' | 5.6 | 1.3 | 5.8 | 6.9 | 4.9 | 0.9 | 4.5 | 5.9 | −0.7 |
| go-go' | 10.8 | 3.0 | 9.9 | 13.7 | 9.4 | 2.5 | 7.7 | 12.7 | −1.4 |
| zy-zy' | 8.8 | 1.4 | 8.1 | 10.3 | 7.2 | 1.2 | 7.3 | 8.4 | −1.6 |
| mr-mr' | 20.1 | 3.2 | 21.0 | 23.4 | 20.0 | 3.3 | 21.3 | 24.0 | −0.1 |
| mmb-mmb' | 8.9 | 2.1 | 8.2 | 11.4 | 8.3 | 1.9 | 7.6 | 10.0 | −0.6 |
| FSTT Mean | – | – | – | – | – | – | – | – | 0.1 |
| Females (f) | Males (m) | Δsex | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n = 57; age = 18–28 yrs | n = 43; age = 18–27 yrs | ||||||||
| x̄ | s | Shorth | Shormax | x̄ | s | Shorth | Shormax | (x̄m − x̄f) | |
| Height (mm) | 1649 | 72 | – | – | 1837 | 75 | – | – | 188 |
| Mass (kg) | 63 | 11 | – | – | 93 | 19 | – | – | 30 |
| BMI (kg/m2) | 23 | 4 | – | – | 28 | 5 | – | – | 4 |
| Facial soft-tissue thicknesses (mm) | |||||||||
| g-g' | 4.7 | 0.8 | 4.3 | 6.0 | 5.1 | 0.7 | 5.0 | 6.0 | 0.4 |
| n-se' | 5.3 | 1.0 | 4.7 | 6.0 | 5.9 | 1.1 | 5.3 | 7.0 | 0.6 |
| rhi-rhi' | 1.9 | 0.4 | 2.0 | 2.0 | 2.0 | 0.4 | 2.0 | 2.0 | 0.1 |
| mp-mp' | 9.4 | 1.7 | 8.9 | 11.0 | 11.6 | 2.2 | 11.0 | 13.0 | 2.2 |
| sm-sm' | 10.3 | 1.3 | 9.4 | 12.0 | 10.9 | 1.6 | 10.5 | 12.0 | 0.6 |
| pg-pg' | 9.1 | 2.0 | 8.1 | 11.0 | 10.0 | 2.5 | 8.6 | 12.0 | 0.9 |
| me-me' | 5.8 | 1.4 | 5.4 | 7.0 | 6.9 | 1.6 | 6.3 | 8.8 | 1.1 |
| mso-mso' | 5.4 | 0.8 | 5.2 | 6.0 | 5.5 | 1.2 | 5.5 | 7.0 | 0.1 |
| mio-mio' | 6.0 | 1.1 | 5.5 | 7.0 | 5.7 | 1.5 | 5.4 | 7.0 | −0.3 |
| ac-ac' | 8.1 | 2.0 | 6.9 | 10.0 | 7.9 | 2.0 | 6.9 | 9.2 | −0.2 |
| go-go' | 18.2 | 2.9 | 16.8 | 21.0 | 20.0 | 3.9 | 18.2 | 23.5 | 1.8 |
| sC-sC' | 9.4 | 1.6 | 9.3 | 11.5 | 11.5 | 2.5 | 11.0 | 14.0 | 2.1 |
| iC-iC' | 9.6 | 1.4 | 8.9 | 11.0 | 11.2 | 2.2 | 9.9 | 13.8 | 1.6 |
| ecm2-sM2' | 27.5 | 3.1 | 27.1 | 31.0 | 28.4 | 4.1 | 27.7 | 34.0 | 0.9 |
| mmb-mmb' | 14.2 | 3.0 | 13.9 | 17.0 | 14.5 | 4.5 | 14.3 | 19.5 | 0.3 |
| FSTT mean | – | – | – | – | – | – | – | – | 0.8 |
| Females (f) | Males (m) | Δsex | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n = 25; 18–29 yrs | n = 35; age = 18–30 yrs | ||||||||
| x̄ | s | Shorth | Shormax | x̄ | s | Shorth | Shormax | (x̄m - x̄f) | |
| Height (mm) | 1658 | 60 | - | - | 1798 | 83 | - | - | 140 |
| Mass (kg) | 71 | 18 | - | - | 85 | 18 | - | - | 14 |
| BMI (kg/m2) | 26 | 6 | - | - | 26 | 5 | - | - | 0 |
| Facial soft-tissue thicknesses (mm) | |||||||||
| g-g' | 4.7 | 1.0 | 4.4 | 6.0 | 5.6 | 1.1 | 5.3 | 7.0 | 0.9 |
| n-se' | 5.8 | 1.0 | 5.6 | 7.0 | 6.7 | 1.0 | 6.5 | 7.8 | 0.9 |
| rhi-rhi' | 1.8 | 0.5 | 2.0 | 2.0 | 2.3 | 0.5 | 2.0 | 3.0 | 0.5 |
| mp-mp' | 9.5 | 1.9 | 8.9 | 11.0 | 12.8 | 2.1 | 13.0 | 14.0 | 3.3 |
| sm-sm' | 12.1 | 2.8 | 11.3 | 15.0 | 12.8 | 2.0 | 12.2 | 16.0 | 0.7 |
| pg-pg' | 11.1 | 2.8 | 9.9 | 14.0 | 12.5 | 2.9 | 10.7 | 14.0 | 1.4 |
| me-me' | 6.8 | 2.0 | 5.6 | 8.8 | 8.8 | 2.4 | 7.9 | 11.0 | 2.0 |
| mso-mso' | 6.3 | 1.3 | 5.4 | 7.0 | 6.5 | 1.4 | 6.5 | 8.0 | 0.2 |
| mio-mio' | 6.7 | 1.4 | 6.5 | 8.0 | 6.5 | 2.0 | 5.7 | 7.0 | −0.2 |
| ac-ac' | 8.3 | 2.5 | 7.1 | 11.0 | 9.5 | 2.8 | 7.7 | 12.0 | 1.2 |
| go-go' | 18.9 | 4.0 | 17.0 | 23.0 | 21.5 | 3.7 | 19.7 | 24.0 | 2.6 |
| sC-sC' | 10.6 | 1.9 | 11.1 | 14.0 | 13.1 | 1.9 | 12.8 | 15.0 | 2.5 |
| iC-iC' | 11.3 | 2.4 | 12.8 | 14.0 | 14.3 | 2.7 | 13.3 | 17.0 | 3.0 |
| ecm2-sM2' | 28.2 | 4.9 | 30.6 | 34.0 | 28.4 | 3.2 | 27.1 | 32.5 | 0.2 |
| mmb-mmb' | 13.8 | 4.3 | 11.7 | 19.0 | 14.1 | 3.9 | 11.4 | 18.5 | 0.3 |
| FSTT mean | – | – | – | – | – | – | – | – | 1.3 |
| Females (f) | Males (m) | Δsex | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n = 25; age = 31–58 yrs | n = 25; age = 30–58 yrs | ||||||||
| x̄ | s | Shorth | Shormax | x̄ | s | Shorth | Shormax | (x̄m - x̄f) | |
| Mass (kg) | 62 | 4 | - | - | 71 | 5 | - | - | 9 |
| Facial soft-tissue thicknesses (mm) | |||||||||
| sg-sg' | 4.3 | 1.0 | 4.5 | 5.7 | 4.3 | 0.8 | 3.7 | 5.0 | 0.0 |
| g-g' | 6.9 | 0.9 | 6.8 | 7.6 | 6.7 | 1.0 | 6.7 | 8.1 | −0.2 |
| n-se' | 7.6 | 1.0 | 8.2 | 8.7 | 7.9 | 0.9 | 7.3 | 8.9 | 0.3 |
| rhi-rhi' | 2.8 | 0.7 | 2.2 | 3.4 | 3.3 | 0.5 | 3.4 | 3.8 | 0.5 |
| mp-mp' | 11.5 | 1.5 | 11.3 | 13.1 | 12.6 | 1.2 | 11.9 | 13.2 | 1.1 |
| pr-ls' | 11.0 | 1.1 | 10.9 | 12.4 | 11.9 | 1.6 | 10.9 | 13.5 | 0.9 |
| id-li' | 12.0 | 1.4 | 12.1 | 13.7 | 12.8 | 1.4 | 12.8 | 14.6 | 0.8 |
| sm-sm' | 10.2 | 1.3 | 10.4 | 11.5 | 10.6 | 1.2 | 10.4 | 12.4 | 0.4 |
| pg-pg' | 12.5 | 1.7 | 13.1 | 15.1 | 12.3 | 1.5 | 11.4 | 13.8 | −0.2 |
| me-me' | 6.7 | 1.5 | 6.4 | 7.9 | 8.1 | 1.1 | 8.0 | 8.9 | 1.4 |
| mso-mso' | 7.5 | 1.3 | 8.0 | 8.9 | 7.1 | 0.8 | 6.9 | 7.9 | −0.4 |
| mio-mio' | 6.8 | 1.4 | 7.3 | 8.3 | 5.6 | 1.6 | 4.8 | 6.9 | −1.2 |
| ac-ac' | 8.7 | 0.9 | 8.9 | 9.8 | 9.4 | 1.5 | 8.8 | 11.5 | 0.7 |
| zy-zy' | 9.9 | 2.1 | 9.4 | 12.0 | 8.1 | 1.4 | 7.4 | 9.6 | −1.8 |
| go-go' | 19.0 | 3.2 | 19.3 | 21.7 | 18.0 | 4.0 | 17.0 | 25.4 | −1.0 |
| ecm2-sM2' | 27.8 | 2.9 | 27.6 | 30.6 | 27.1 | 2.4 | 27.9 | 29.9 | −0.7 |
| ecm2-iM2' | 23.1 | 3.4 | 24.3 | 26.5 | 22.1 | 2.7 | 20.0 | 25.0 | −1.0 |
| mr-mr' | 18.8 | 3.9 | 18.9 | 24.5 | 18.1 | 2.1 | 18.9 | 20.4 | −0.7 |
| mmb-mmb' | 12.6 | 1.7 | 11.5 | 13.8 | 10.9 | 2.2 | 9.5 | 12.8 | −1.7 |
| FSTT mean | – | – | – | – | – | – | – | – | −0.1 |
Repeat FSTT measurements at six landmarks for the Australian White data (g′, n′, pg′, go′, zy′, mio′) yielded a mean technical error of measurement (TEM) equal to 0.8 mm. Converted to a relative-TEM this value corresponds to 10%; which is lower than the absolute (positive signed converted) sex difference at the same six landmarks (12%). These results indicate, at least with regards to the Australian White data, that the sex difference exceeds the measurement error, thereby awarding confidence that a small mean sex difference in FSTTs does, in fact, exist (it is in the range of 2 − 12%, but probably closer to the smaller end of this size spectrum).
When sex and the four BMI categories were tested by MANOVA, the results revealed that sex was routinely statistically significant; however, BMI was not (Table 7). Eta-squared values for sex were also lower than those for BMI, ranging from 2 to 9% (Table 7). As for other studies (De Greef et al., 2009; Stephan & Simpson, 2008) males tended to possess larger mean FSTT overall (Δsex = −6%; Table 8), however, females frequently displayed larger magnitudes at landmarks in the fleshy region of the cheeks (see mio′, ac′, zy′, go′, sM2′, iM2′, mr′, mmb′; Table 8).
| Sex | BMI | Sex × BMI | ||
|---|---|---|---|---|
| Australian Whites | η2 | 0.05 | 0.08 | 0.05 |
| p | .11 | .19 | .38 | |
| American Whites | η2 | 0.03 | 0.05 | 0.02 |
| p | <.01 | .16 | .79 | |
| American Blacks | η2 | 0.09 | 0.02 | 0.02 |
| p | <.01 | .72 | .61 | |
| Turks | η2 | 0.06 | – | – |
| p | <.01 | – | – | |
- Bold values show p ≤ .05.
| Raw data | Normalized data | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass | Stature | BMI | ||||||||||||
| AusW | AmW | AmB | T | AusW | AmW | AmB | T | AusW | AmW | AmB | AusW | AmW | AMB | |
| m-m' | −5 | x | x | x | 19 | x | x | x | 3 | x | x | 3 | x | x |
| sg-sg' | x | x | x | −1 | x | x | x | 13 | x | x | x | x | x | x |
| g-g' | 3 | −8 | −19 | 2 | 24 | 26 | 2 | 16 | 11 | 3 | −9 | 10 | 8 | −16 |
| n-se' | −15 | −11 | −17 | −5 | 10 | 23 | 4 | 10 | −6 | 0 | −8 | −6 | 6 | −14 |
| rhi-rhi' | −7 | −4 | −24 | −17 | 17 | 29 | −2 | −1 | 2 | 7 | −15 | 1 | 12 | −21 |
| mp-mp' | −11 | −23 | −35 | −10 | 14 | 16 | −12 | 5 | −2 | −11 | −24 | −2 | −4 | −32 |
| pr-ls' | x | x | x | −8 | x | x | x | 7 | x | x | x | x | x | x |
| id-li' | x | x | x | −7 | x | x | x | 8 | x | x | x | x | x | x |
| sm-sm' | −8 | −6 | −5 | −4 | 15 | 27 | 14 | 10 | 1 | 5 | 3 | −1 | 10 | −2 |
| pg-pg' | −10 | −10 | −12 | 2 | 15 | 26 | 7 | 16 | −1 | 1 | −3 | 0 | 7 | −10 |
| me-me' | −12 | −19 | −30 | −21 | 13 | 19 | −8 | −5 | −3 | −7 | −20 | −3 | 0 | −28 |
| mso-mso' | −7 | −1 | −3 | 5 | 16 | 30 | 15 | 18 | 2 | 9 | 5 | 1 | 13 | −1 |
| mio-mio' | 14 | 4 | 3 | 18 | 33 | 34 | 18 | 29 | 21 | 14 | 10 | 20 | 19 | 4 |
| ac-ac' | x | 3 | −14 | −8 | x | 33 | 7 | 7 | x | 13 | −5 | x | 17 | −11 |
| zy-zy' | 18 | x | x | 19 | 36 | x | x | 30 | 24 | x | x | 24 | x | x |
| go-go' | 13 | −10 | −14 | 5 | 33 | 25 | 6 | 19 | 21 | 1 | −4 | 21 | 7 | −12 |
| sC-sC' | x | −22 | −24 | x | x | 16 | −2 | x | x | −10 | −14 | x | −3 | −21 |
| iC-iC' | x | −17 | −27 | x | x | 21 | −5 | x | x | −5 | −17 | x | 2 | −24 |
| sM2-sM2' | x | −4 | −1 | 2 | x | 28 | 16 | 16 | x | 7 | 7 | x | 11 | 1 |
| iM2-iM2' | x | x | x | 4 | x | x | x | 17 | x | x | x | x | x | x |
| mr-mr' | 0 | x | x | 4 | 23 | x | x | 17 | 9 | x | x | 8 | x | x |
| mmb-mmb' | 7 | −2 | −2 | 13 | 28 | 30 | 15 | 26 | 15 | 8 | 6 | 15 | 14 | 0 |
| Mean | −2 | −9 | −15 | 0 | 21 | 26 | 5 | 13 | 7 | 2 | −6 | 7 | 8 | −12 |
| Grand mean | −6 | 16 | 1 | 1 | ||||||||||
After normalization by mass, the sex difference reversed (become positive, with females larger than males; Table 8) and increased in percentage magnitude by 2.7× compared to the raw data (Figure 5 and Table 8). Height and BMI normalized data showed only weak positive trends (+1% differences between the sexes). The squaring of the height contribution to the denominator of the BMI calculation is the reason for the poor performance of the BMI variable, even though BMI draws on the well-correlated body-mass for the numerator.
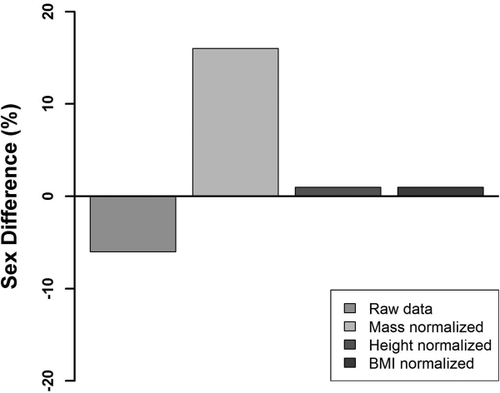
Overarching percentage sex differences in 142 females and 120 males (all four studies combined) for raw and body-composition normalized data. Negative values indicate M > F. Positive values indicate F > M.
Attempts to quantify allometry of the FSTTs proved unsuccessful due to large variance in the FSTT compared to their small values, producing tight circular data clusters on the Log10 transformation scale. Without clearly orientated linear distributions, trend lines using the Standard Major Axes alternated in direction across the samples for the same landmark warning against robustness and utility of these descriptors. Consequently, this component of the study will not be further discussed. For further comment on sampling error, measurement error, and other noise in FSTTs see: Stephan (2014, 2015), Stephan et al. (2015), and Stephan & Simpson (2008).
4 Discussion
After mass normalization FSTTs possessed a reversed pattern of sexual dimorphism in contrast to universally accepted views that males hold larger values than females (De Greef et al., 2006; Dong et al., 2012; Helmer, 1984; Sahni et al., 2008; Simpson & Henneberg, 2002; Wang et al., 2016; Wilkinson, 2004). After standardizing for body mass, females displayed larger FSTTs than males and with a 2.7× larger mean magnitude (16%) than the mean raw result (−6%). Trends were in the same direction across all four samples investigated, which suggests good reproducibility. This overturns opinions held for over the past 120 years that males generally hold larger FSTTs than females.
In addition to reversing the raw data trend and increasing the difference magnitude by 2.7×, the mass-normalized pattern was more generalizable across the face. The mass-normalized F > M pattern holds for 88% of all facial landmarks investigated across the four samples examined in this study (exceptions observed at rhi, mp, me, sC, iC, but not for all samples), compared to only 70% of landmarks when using the M > F raw data trend (here exceptions occur at g, pg, mso, mio, ac, zy, go, sM2, iM2, mr, and mmb and sometimes for all four samples; Table 8).
While BMI and stature were found to correlate with raw FSTTs, the stature normalization did not enhance the sex difference—in fact it reduced it. This likely occurs because body height, which is largely determined by skeletal structure, does not tightly follow fluctuations in soft tissue composition over short time frames, reducing its potency as a covariate. This also limits the utility of skeletal-mass as a proxy for body mass, as otherwise might be useful for craniofacial identification where skeletons are the main subject of analyses.
While data pooling across the sexes to boost reliability is adequately justified on the grounds of group overlap, measurement errors, sampling, and other data noise (Stephan, 2014; Stephan et al., 2005, 2015; Stephan & Simpson, 2008), the body-scale normalized sex-trends add further justification to the data pooling approach and extinguishes any lingering concern about this approach's validity (İşcan & Steyn, 2013). There is little risk of jeopardizing any sex differences by data pooling because sexual dimorphism in FSTT is manifested most strongly relative to body mass, not the raw FSTT measurements. As a result of this property and the increased reliability due to increased sample size, the pooled data are preferable for casework application in contrast to their sex-separated counterparts.
This study demonstrates how body-scale normalization can dramatically alter interpretations of sexual dimorphism in modern humans (e.g., reverses interpretations of FSTT trends); and highlights the value of joint consideration of both the raw and the relative differences. The generalization that males hold larger raw FSTT values than females, while true to some extent, is a very imprecise and practically limiting way to view the FSTT data. Males have only slightly larger raw values than females, and these do not occur in all regions of the face. When body mass is controlled for, females have much larger values than males, and more uniformly so across the face. An appreciation of both the raw and the relative relationships are important for a comprehensive understanding of human facial soft tissue morphology, but the latter factor is key for providing simpler, more reliable, and more powerful understandings of human variation in the facial soft tissues.
In this study we were unable to investigate FSTT relationships for all population groups, including individuals of Asian descent. However, there is little reason to suspect that the above described relationships will not be generalizable to these other groups because basic patterns of human sexual dimorphism in body scale and body composition (males larger than females) are widely known to be universal in humans (Bogin, 1999; Wells, 2007). For example, lighter body masses are also reported for Chinese females compared to Chinese males (Xu, Shu, & Han, 2015) and, in combination with larger raw FSTTs reported for female Chinese samples (Jia et al., 2016), all indicators are that the above described mass-normalized trends apply.
While the data presented here extensively validate FSTT data pooling by sex, the question can be posed, should similar data pooling approaches apply to BMI categories? In short our answer is “yes”. Body mass is presently difficult to predict from the skeleton alone, making correct assignment of individuals to BMI categories on skeletal indicators difficult (Stephan et al., 2013). Consequently, FSTT and BMI values should be retained in their native (continuous) format, especially in training samples for statistical models, which means that the data take the form of a single set (or pool). For any estimate of an individual's FSTT then, two statistics should be employed as proxies to individual values: the shorth—or the mean of the densest half; and the 75-shormax—the 75th percentile between the shorth and the maximum value. The shorth provides a point estimate of the peak of the FSTT data distribution (i.e., the most common data) and the 75-shormax provides a central tendency approximation for larger individuals, with higher BMI values, who fall within the right tail of the FSTT distribution. This pooled treatment of the data is favourable because it utilizes the correlations between FSTT and BMI without forcing any arbitrarily defined categories.
Similar to sex and BMI, data pooling for FSTTs may also be applicable to ancestry since current ancestral comparisons fall short of accounting for sampling and other measurement errors (Stephan, 2015b) risking the interpretation of data noise for real ancestral effects (Stephan, 2014, 2015b; Stephan et al., 2013, 2015; Stephan & Simpson, 2008). Without good evidence that the magnitude of population-based differences exceeds the error associated with sampling and other measurement, data pooling is the safest and most conservative course of action. As for sexual dimorphism, this procedure may be further legitimized if ancestral differences are found to be best expressed more strongly as a relative function of body size in contrast to their native raw format.
Acknowledgments
Special thanks go to: Ismail Hizliol for assistance with the collection of the Turkish FSTT data; the team of Ginesse Listi, Mary Manhein, Robert Barsley, Robert Musselman, Eileen Barrow, and Douglas Ubelaker for open access to their raw data via CRANIOFACIALidentification.com; Jodi Caple for illustrations used in Figure 2; Emma Sievwright for the Jia et al. (2016) reference; and Paul Emanovsky and John Byrd for generic discussions on allometry and the Jungers et al. (1995) and Mosimann and James (1979) references.




