Adaptive observer for nonlinear fractional-order systems
Corresponding Author
Ibrahima N'doye
Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900 Saudi Arabia
Correspondence to: Ibrahima N'doye, Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, 23955-6900.
E-mail: [email protected]
Search for more papers by this authorTaous-Meriem Laleg-Kirati
Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900 Saudi Arabia
Search for more papers by this authorMohamed Darouach
Research Center for Automatic Control of Nancy (CRAN UMR, 7039, CNRS), University of Lorraine, IUT de Longwy, 186 rue de Lorraine 54400 Cosnes et Romain, France
Search for more papers by this authorHolger Voos
Faculty of Science, Technology and Communication (FSTC), University of Luxembourg, 6, rue Richard Coudenhove-Kalergi, L-1359 Luxembourg
Search for more papers by this authorCorresponding Author
Ibrahima N'doye
Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900 Saudi Arabia
Correspondence to: Ibrahima N'doye, Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, 23955-6900.
E-mail: [email protected]
Search for more papers by this authorTaous-Meriem Laleg-Kirati
Computer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900 Saudi Arabia
Search for more papers by this authorMohamed Darouach
Research Center for Automatic Control of Nancy (CRAN UMR, 7039, CNRS), University of Lorraine, IUT de Longwy, 186 rue de Lorraine 54400 Cosnes et Romain, France
Search for more papers by this authorHolger Voos
Faculty of Science, Technology and Communication (FSTC), University of Luxembourg, 6, rue Richard Coudenhove-Kalergi, L-1359 Luxembourg
Search for more papers by this authorSummary
In this paper, an adaptive observer is proposed for the joint estimation of states and parameters of a fractional nonlinear system with external perturbations. The convergence of the proposed observer is derived in terms of linear matrix inequalities (LMIs) by using an indirect Lyapunov method.The proposed
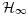adaptive observer is also robust against Lipschitz additive nonlinear uncertainty. The performance of the observer is illustrated through some examples including the chaotic Lorenz and Lü's systems. Copyright © 2016 John Wiley & Sons, Ltd.
References
- 1Cole K Electric conductance of biological systems. Proceeding Cold Spring Harbor Symposia Quantitative Biology, New York, USA, 1933; 107–116.
- 2Laskin N. Fractional market dynamics. Physica A: Statistical Mechanics and its Applications 2000; 287: 482–492.
- 3Engheta N. On fractional calculus and fractional multipoles in electromagnetism. IEEE Transaction Antennas and Propagation 1996; 44: 554–566.
- 4Sun H, Abdelwahad A, Onaral B. Linear approximation of transfer function with a pole of fractional order. IEEE Transactions on Automatic Control 1984; 29: 441–444.
- 5Gabano DJ, Poinot T. Estimation of thermal parameters using fractional modelling. Signal Processing 2011; 91: 938–948.
- 6Bagley R, Calico R. Fractional order state equations for the control of viscoelastically damped structures. Journal of Guidance, Control, and Dynamics 1991; 14: 304–311.
- 7Wang CJ. Realizations of generalized warburg impedance with RC ladder networks and transmission lines. Journal of the Electrochemical Society 1987; 134: 1915–1920.
- 8Podlubny I Fractional Differential Equations. Academic Press: New York, 1999.
- 9Monje CA, Chen YQ, Vinagre BM, Xue D, Feliu V Fractional-Order Systems and Controls: Fundamentals and Applications. Springer: Berlin, 2010.
- 10Petrás̆ I Fractional-Order Nonlinear Systems : Modeling, Analysis and Simulation. Springer: Berlin, 2011.
10.1007/978-3-642-18101-6 Google Scholar
- 11Liu DY, Laleg-Kirati TM. Robust fractional order differentiators using generalized modulating functions method. Signal Processing 2014; 107: 395–406.
- 12Rapaić MR, Pisano A. Variable-order fractional operators for adaptive order and parameter estimation. IEEE Transactions on Automatic Control 2014; 59: 798–803.
- 13Boroujeni EA, Momeni HR. Non-fragile nonlinear fractional order observer design for a class of nonlinear fractional order systems. Signal Processing 2012; 92: 2365–2370.
- 14Lang YH, Zhou Y. Non-fragile observer-based robust control for a class of fractional-order nonlinear systems. Systems & Control Letters 2013; 62: 1143–1150.
- 15Das S Functional Fractional Calculus for System Identification and Controls. Springer: Heidelberg, 2008.
- 16Montseny G. Diffusive representation of pseudo-differential time-operators. ESAIM: Fractional Differential Systems : Models, Methods and Applications 1998; 5: 1318–1326.
- 17Sabatier J, Farges C, Trigeassou JC. Fractional systems state space description : some wrong ideas and proposed solutions. Journal of Vibration and Control 2014; 20: 1076–1084.
- 18Heleschewitz D, Matignon D. Diffusive realizations of fractional integro-differential operators : Structure analysis under approximation. IFAC Conference on System, Structure and Control 1998; 2: 243248.
- 19Trigeassou JC, Maamri N. Initial conditions and initialization of linear fractional differential equations. Signal Processing 2011; 91: 427–436.
- 20Trigeassou J, Maamri N, Sabatier J, Oustaloup A. A Lyapunov approach to the stability of fractional differential equations. Signal Processing 2011; 91: 437–445.
- 21Bettayeb M, Djennoune S. Design of sliding mode controllers for nonlinear fractional-order systems via diffusive representation. Nonlinear Dynamics 2016; 84: 593–605.
- 22Matignon D, Andréa-Novel B Observer-based control for fractional differential systems. Proceeding IEEE Conference Decision & Control, San Diego, USA, 1997.
- 23Darouach M, Zasadzinski M, Xu S. Full-order observers for linear systems with unknown inputs. IEEE Transactions on Automatic Control 1994; 39: 606–609.
- 24Khargonakar P, Petersen I, Zhou K. Robust stabilization of uncertain linear systems : quadratic stability and
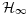control theory. IEEE Transactions on Automatic Control 1990; 35: 356–361.
- 25Cho Y, Rajamani R. A systematic approach to adaptive observer synthesis for nonlinear systems. IEEE Transactions on Automatic Control 1997; 42: 534–537.
- 26Boyd S, El Ghaoui L, Féron E, Balakrishnan V Linear Matrix Inequality in Systems and Control Theory. SIAM: Philadelphia, 1994.
10.1137/1.9781611970777 Google Scholar
- 27Krstic M, Kanellakopoulos I, Kokotovic P Nonlinear and Adaptive Control Design. Wiley: New York, 1995.
- 28Abbaszadeh M, Marquez JH Robust
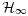observer design for a class of nonlinear uncertain systems via convex optimization. Proceedings IEEE American Control Conference, New-York, USA, 2007.
- 29Abbaszadeh M, Marquez JH. LMI optimization approach to robust
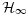observer design and static output feedback stabilization for discrete-time nonlinear uncertain systems. International Journal of Robust and Nonlinear Control 2009; 19(3): 313–340.
- 30Abbaszadeh M, Marquez JH. Dynamical robust
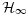observer for nonlinear uncertain systems : an LMI approach. Journal of the Franklin Institute 2009; 347(7): 1227–1241.
- 31Abbaszadeh M, Marquez JH. A generalized framework for robust nonlinear
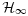filtering of Lipschitz descriptor systems with parametric and nonlinear uncertainties. Automatica 2012; 48: 894–900.
- 32Tavazoei SM, Haeri M. Limitations of frequency domain approximation for detecting chaos in fractional order systems. Nonlinear Analysis 2008; 69: 1299–1320.
- 33Tavazoei SM, Haeri M. A necessary condition for double scroll attractor existence in fractional-order systems. Physics Letters A 2007; 367: 102–113.
- 34Deng HW, Li PC. Chaos synchronization of the fractional Lu system. Physica A 2005; 353: 61–72.
