A one-dimensional Pólya-Szegö type principle is proved for fractional order derivatives. As a consequence, the boundedness of the decreasing rearrangement operator is established in Besov spaces 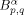equation image (0, l ) for α∈ (0,1+1/p ).

References

[AL] Almgren J., F. J. , and Lieb, E.H.: Symmetric Rearrangement Is Sometimes Continuous, J. Amer. Math. Soc. 2 (1989), 683–773
10.2307/1990893
Google Scholar
[B] Baernstein II, A.: A Unified Approach to Symmetrization. In: Partial Diff. Eq. of Elliptic Type, A. Alvino, E. Fabes and G. Talenti eds., Symposia Math. 35, Cambridge Univ. Press, 1994
Google Scholar
[BS] Bennett, C., and Sharpley, R.: Interpolation of Operators, Academic Press, Boston, 1988
Google Scholar
[BM] Bourdaud, G., and Meyer, Y.: Fonctions qui Opèrent sur les Espaces de Sobolev, J. Funct. Anal. 91 (1991), 351–360
10.1016/0022-1236(91)90006-Q
Web of Science® Google Scholar
[Ch] Chiti, G.: Rearrangements of Functions and Convergence in Orlicz Spaces, Appl. Anal. 9 (1979), 23–27
10.1080/00036817908839248
Google Scholar
[Ci] Cianchi, A.: Second Order Derivatives and Rearrangements, Duke Math. J. 105 (2000), 355–385
10.1215/S0012-7094-00-10531-5
Web of Science® Google Scholar
[GR] Garsia, A.M., and Rodemich, E.: Monotonicity of Certain Functionals under Rearrangements, Ann. Inst. Fourier, Grenoble 24 (1974), 67–116
10.5802/aif.507
Web of Science® Google Scholar
[K] Kawohl, B.: Rearrangements and Convexity of Level Sets in PDE, Lecture Notes in Math. 1150, Springer-Verlag, Berlin–New York, 1985
Google Scholar
[O] Oswald, P.: On the Boundedness of the Mapping f=|f| in Besov Spaces, Comment. Math. Univ. Carolinae 33 (1992), 57–66
Google Scholar
[S] Savaré, G.: On the Regularity of the Positive Part of Functions, Nonlinear Anal. 27 (1996), 1055–1074
10.1016/0362-546X(95)00104-4
Web of Science® Google Scholar
[Ta] Tartar, L.: Interpolation non Linéaire et Régularité, J. Funct. Anal. 9 (1972), 468–489
10.1016/0022-1236(72)90022-5
Google Scholar
[Tr1] Triebel, H.: Theory of Function Spaces II, Birkhäuser, Basel, 1992
Google Scholar
[Tr2] Triebel, H.: Truncations of Functions, Forum Math. 12 (2000), 731–756
10.1515/form.2000.026
Web of Science® Google Scholar
[Z] Ziemer, W.P.: Weakly Differentiable Functions, Springer-Verlag, New York, 1989
Google Scholar

Citing Literature

Volume230, Issue1

October 2001

Pages 19-35

Rearrangements of Functions in Besov Spaces

Abstract

References

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Rearrangements of Functions in Besov Spaces

Abstract

References

Citing Literature

References

Related

Information