Activity-dependent reconfiguration of the effective dendritic field of motoneurons
Abstract
A neuron in vivo receives a continuous bombardment of synaptic inputs that modify the integrative properties of dendritic arborizations by changing the specific membrane resistance (Rm). To address the mechanisms by which the synaptic background activity transforms the charge transfer effectiveness (Tx) of a dendritic arborization, the authors simulated a neuron at rest and a highly excited neuron. After in vivo identification of the motoneurons recorded and stained intracellularly, the motoneuron arborizations were reconstructed at high spatial resolution. The neuronal model was constrained by the geometric data describing the numerized arborization. The electrotonic structure and Tx were computed under different Rm values to mimic a highly excited neuron (1 kOhm.cm2) and a neuron at rest (100 kOhm.cm2). The authors found that the shape and the size of the effective dendritic fields varied in the function of Rm. In the highly excited neuron, the effective dendritic field was reduced spatially by switching off most of the distal dendritic branches, which were disconnected functionally from the somata. At rest, the entire dendritic field was highly efficient in transferring current to the somata, but there was a lack of spatial discrimination. Because the large motoneurons are more sensitive to variations in the upper range of Rm, they switch off their distal dendrites before the small motoneurons. Thus, the same anatomic structure that shrinks or expands according to the background synaptic activity can select the types of its synaptic inputs. The results of this study demonstrate that these reconfigurations of the effective dendritic field of the motoneurons are activity-dependent and geometry-dependent. J. Comp. Neurol. 422:18–34, 2000. © 2000 Wiley-Liss, Inc.
The structure and transfer properties of dendritic arborizations are crucial for synaptic integration and for input-output conversion in the central neurons that receive >90% of their synaptic inputs through dendrites (for review, see Mel, 1994). A functionally relevant measure of the effectiveness of various synaptic inputs is the net current delivered to the soma, because the firing rate of motoneurons is in direct proportion to this current (Granit et al., 1966; Barrett and Crill, 1974; Heckman and Binder, 1988; Bernander et al., 1994; Powers and Binder, 1995). It generally is admitted that synapses at different dendritic sites are effective unequally in their contribution to the cell output. Numerous attempts to determine a relation between the structure of dendritic arborizations and the integrative function of the neuron (for reviews, see Lüscher and Clamann, 1992; Horcholle-Bossavit et al., 1997) have shown that the passive transfer properties of the dendrites are expressed best by their electrotonic structure, which integrates morphologic data and membrane biophysical properties. Whereas the geometric parameters are likely to be obtained at high spatial resolution, the electrical parameters, such as the specific membrane resistance (Rm), the capacitance (Cm), and the specific cytoplasm resistance (Ri), are always estimated rather than measured. A simple and faithful representation of the electrotonic structure of complex arborizations can be obtained by using the somatofugal voltage attenuation profiles along each dendritic path in physical coordinates (Bras et al., 1987a, 1993). This representation is identical to the path profiles of the somatopetal current transfer effectiveness (Barrett and Crill, 1974; Bras et al., 1993; Korogod et al., 1994; Korogod, 1996; Mainen et al., 1996; Carnevale et al., 1997). Considering these profiles, one can see how geometry governs the transfer effectiveness of different dendritic paths. The path gradient of voltage is sensitive to inhomogeneities of the core resistance. Both the voltage and the current transfer along dendritic paths (and, thus, the electrotonic structure) depend on the value of Rm.
Functionally, Rm and whole cell input resistance (RN) depend on synaptic activity (Smith et al., 1967; Barrett and Crill, 1974; Bernander et al., 1991). A recent investigation estimates the impact of spontaneous synaptic activity on RN of cortical neurons in vivo. During intense synaptic bombardment, RN can be reduced by up to 70% (Paré et al., 1998). In our previous simulation studies, we suggested that the activity-dependent reconfiguration of the electrotonic structure observed under different Rm was a kind of postsynaptic plasticity in motoneurons (Bras et al., 1993; Korogod et al., 1994). From these geometry- and activity-dependent changes in the electrotonic structure of complex arborized dendritic paths, one can expect a reconfiguration of the effective functional size and shape of the dendritic fields. Surprisingly, this issue was never considered explicitly for motoneurons, which functionally are the best defined cells of the central nervous system, with well-developed dendritic fields that are covered densely by synapses.
The issue of the functionally effective size and shape of the dendritic field of a single central neuron rarely is assessed. Studies of pyramidal neurons of the visual cortex have revealed that the synaptic background activity can control the spatial and temporal integrative properties of single neurons (Koch, 1984; Bernander et al., 1991; Mel et al., 1998). Along the same lines, Paré et al. (1998) suggested that “the intense synaptic bombardment present in vivo may subdivide the dendritic tree of pyramidal neurons into localized regions that, to some extent, process synaptic inputs independently.” Thus, depending on the differential effectiveness of the synapses received by the different dendritic branches, the whole dendritic field can be mapped, and different efficient dendritic domains can be distinguished.
In the present work, we compare the changes of the charge transfer effectiveness resulting from changing the level of synaptic bombardment on morphologically different dendritic arborizations from different types of motoneurons in different species. We analyze the effects of path structure and branching asymmetry on the reconfiguration of the electrotonic structure. The spatial extent of the efficient dendritic domains is investigated under different Rm, ranging from low values to mimic high presynaptic activities to high values for simulating a neuron at rest. We find that the efficient domain of the dendritic fields can undergo significant spatial modifications that are correlated with the level of activity of the neuron. The efficient dendritic fields shrink when Rm is reduced as a result of increased tonic synaptic excitation. We show that these dynamic changes are activity-dependent as well as geometry-dependent. We suggest that these changes may be a reflection of a mechanism that adapts the functional size of the dendritic arborizations to different states of neuronal excitability.
Passive dendrites, rather than active dendrites, are analyzed in this study simply because direct and explicit data on the precise spatial localization of voltage-dependent conductances in the dendrites of vertebrates motoneurons are lacking. Furthermore, we have demonstrated that the effect of geometry is similar in passive and active dendrites whatever the cocktails of conductances (Korogod and Kulagina, 1998). Consequently, if geometry is prominent, then a nonuniform Rm over the soma-dendritic surface will not affect our results.
MATERIALS AND METHODS
The four motoneurons analyzed in this work were selected from our library of digitized neurons that were constituted by intracellular staining with horseradish peroxidase (HRP) or biocytin and fully reconstructed neurons obtained in our laboratory and from the authors cited. Some of these authors kindly provided raw data in the form of serial histologic sections. The actual data included one frog lumbar motoneuron (Dityatev et al., 1995; van Pelt et al., 1997), one rat brainstem motoneuron (Bras et al., 1993; Korogod et al., 1994), one rat spinal motoneuron (Chmykhova et al., 1987, 1991), and one cat gastrocnemius motoneuron (specially stained for us by E. Jankowska and H. Bras; Laboratory of Physiology, Göteborg, Sweden). Methods of surgical preparations, electrophysiological recordings, identification of motoneurons by antidromic invasion, intracellular staining, and histologic procedures are described in detail in the published literature cited. These four motoneurons were reconstructed fully with a three-dimensional, computer-aided system in our laboratory by three operators (Bras, Chmykhova, and G.H.-B.). The intensity of staining of distal dendritic branches was one of the criteria for selecting the motoneurons that are described here. The cells in sections showed no evidence of fragmentation, and no extracellular HRP was observed. The integrity of these cells was confirmed further by comparing their total dendritic length with the values reported for cat (Culheim et al., 1987a,b), frog (Dityatev et al., 1995; Matesz et al., 1995), and young rat (Chmykhova et al., 1991) motoneurons.
Morphometric data acquisition
The procedure for data acquisition has been described previously in detail (Bras et al., 1987a, 1993). The labeled neurons were observed by using a microscope (Orthoplan; Leitz, Wetzlar, Germany) with an X/Y (0.1 μm resolution) motorized stage (EK32; Maerzhauser) and microprocessor interface (Lang Electronics) with a Leitz plan ×100/1.25 NA oil-immersion objective lens at a final magnification of ×1,250. A stepping motor controlled the focus in Z direction with a knob at a resolution of 0.1 μm. The dendrites were described as series of data points separated by a three-dimensional distance with a controlled sampling interval ranging from 0.5 μm to 10 μm. The diameter of the profile was measured at 0.2 μm resolution by using a circle displayed on an oscilloscope and adjusted to the dendritic profile. A new data point was entered whenever a change in diameter and/or in direction was observed. Each point was identified by six parameters: sequential number; X, Y, Z coordinates; diameters of the profile; and topological identifier. The computer-microscope system used for this work was implemented by P.G. (Bras et al., 1987a,b) on the basic principles described by Glaser and van der Loos (1965) and Wann et al. (1973). A software program written by P.G. checked the process of data acquisition by the operator. At the end, a dendritic arborization of a single neuron was described by 3,000–25,000 data points, which were stored in a data base together with fiducial marks. A dedicated software program was used for computer reconstruction of the dendritic arborization.
Quantitative morphologic data
The usual morphologic parameters were used to characterize the morphometric and topologic features of the arborizations (Matesz et al., 1995). Metrical properties, such as the number of stem dendrites, the number of dendritic segments (between two branch points or the last branch point and the endpoint), the total length of all dendritic segments, and the length and surface area of each dendrite were considered for each motoneuron. The following topologic parameters were calculated: the complexity index, which is the number of terminal segments of a tree related to the number of its bifurcations and to the total number of segments (Verwer et al., 1992; Dityatev et al., 1995); the coefficient of asymmetry, which is defined as follows: At each bifurcation, the number of terminal tips is partitioned. When they are partitioned into two equal sets, the bifurcation is symmetrical, and the asymmetry value is then 0. The tree asymmetry is the mean value of asymmetry of all bifurcations in a tree (Van Pelt and Verwer, 1986; Van Pelt et al., 1992; Van Pelt and Schierwagen, 1994).
Neuron model
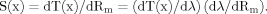 (1)
(1)where λ = (RmD/4Ri)1/2 is the electrotonic length constant, and D is the dendritic diameter. Two kinds of dendritic geometry were explored.
Artificial dendrites with simple geometry.
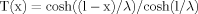 (2)
(2)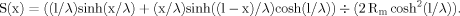 (3)
(3)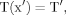 (4)
(4)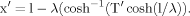 (5)
(5)Reconstructed dendritic arborizations.
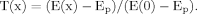 (6)
(6)These computations were made for three different values of Rm of 100, 10, and 1 kOhm.cm2.
RESULTS
Models
To assess the mechanisms of the activity-dependent reconfiguration of effective sizes and shapes of the dendritic field of single neurons, first, we started with simplified models of neurons with rectilinear, uniform, nonbranching dendrites emerging from the soma and spreading in one plane. In these models, the dendrites formed planar dendritic fields with a central symmetry that allowed a representation in the polar coordinates centered at the soma, so that both path and radial distances from the soma were identical.
Symmetrical dendritic field.
Two symmetrical dendritic fields were considered, each of which was formed by four identical dendrites, small in one case and large in the other (Fig. 1). The somatopetal charge transfer effectiveness decayed monotonically with increasing path distance from the soma, with the rate depending on both Rm and dendritic size (Fig. 1, top). The decay in charge transfer was greater for small values of Rm in dendrites of a given size and for the same Rm (e.g., 100 kOhm.cm2). The decay was greater in large dendrites than in small dendrites. The whole dendritic field remained in the high-efficiency domain [T(x) > 0.5] when Rm was sufficiently high. In our examples, these values were ≈4 kOhm.cm2 and 26kOhm.cm2 for small dendrites and large dendrites, respectively. With further decrease in Rm, the path profile, T(x), dropped below T′ = 0.5, so that the distal border of the high-efficiency domain approached the soma progressively. In polar coordinates, the dendritic fields and their high-efficiency domains were concentric circles with the smallest radius for the smallest Rm (Fig. 1, bottom). It is noteworthy that equal decrements in Rm (ΔRm = 0.5 kOhm.cm2 and 5 kOhm.cm2 in small dendrites and large dendrites, respectively) produced unequal decrements in the extent of the high-efficiency domain.
Geometry-dependent, nonhomogenous compression of the high-efficiency domain by homogenous decrements in specific membrane resistance (Rm) computed in two simple simulated neurons. Top left: Small, uniform, symmetrical, rectilinear dendrites (length, 0.5 mm; diameter, 1.5 μm). Top right: Large, uniform, symmetrical, rectilinear dendrites (length, 1.5 mm; diameter, 2 μm). Values of Rm are shown in italics (10 kOHm.cm2 and 100 kOhm.cm2). Dotted lines divide the high-efficiency and low-efficiency domains at charge transfer effectiveness (Tx) = 0.5. Coordinates: Charge transfer effectiveness as a function of path distance (mm) from the soma (0). A decrease in the Rm value provokes a decrease in the Tx value that is different at the same path distance in small and large dendrites. Bottom: Concentric circles (dashed lines) show the path extents of the high-efficiency domains for different Rm values (left, 0.5–4.0; right, 5–26) in four small (left) and large (right) rectilinear dendrites (gray lines) distributed uniformly in the polar angles. The radius of each circle is defined by the path coordinate x′, at which Tx = 0.5.
Asymmetrical dendritic field.
In this case, the field was formed by nine dendrites of equal diameter (2.0 μm). Length, which ranged from 500 μm to 1,500 μm, was a linear function of the polar angle (Fig. 2). Decreasing the value of Rm with equal decrements (ΔRm = 5 kOhm.cm2) led to a reduction in the spatial extent of the high-efficiency domain (Tx > 0.5) with unequal decrements, depending both on Rm and dendritic length. At high Rm (26 kOhm.cm2), the entire field was in the high-efficiency domain, so that the borders of the field (Fig. 2, regular gray spiral) and of the high-efficiency domain (Fig. 2, outermost dotted spiral) coincided. At lower Rm, the Tx = 0.5 zone was bounded by irregular spirals of a smaller centrifugal extent, as shown in Figure 2 by the corresponding dotted lines for Rm in the range of 25–1kOhm.cm2. For a given Rm in this range, the same decrements in Rm led to unequal decrements in the path and the radial field distance to the border of the high-efficiency domain. Beyond a given critical dendritic length, the increments of the path extent increased with a greater rate. It is noteworthy that such behavior of the enveloping borderlines of the high-efficiency domain rendered the smaller domains less asymmetrical. This was due to a decrease in the range of variation of the path extent of the domain. For instance, at the lowest tested Rm (1kOhm.cm2), the high-efficiency domain was nearly circular with the path distance and the radial extent of ≈150 μm. Thus, decreasing the value of Rm resulted in a reduction in size and asymmetry of the functionally high-efficiency domain of the morphologically asymmetrical dendritic field.
Geometry-dependent, nonhomogenous compression of the high-efficiency domain by homogenous decrements in Rm computed in a simulated neuron with uniform asymmetrical dendrites (thin gray lines). The dendritic lengths change from 500 μm to 1,500 μm as a linear function of the polar angle, so that the borderline of the dendritic fields is a regular spiral (thick gray line). The dotted lines show the borderlines of the high-efficient domains for different Rm values (indicated in italics; 1–100 kOhm.cm2). At Rm = 100 kOhm.cm2, all of the dendrites are in the high-efficiency domain, and the borderlines of the corresponding path distance domain (dotted spiral) and of the dendritic field (gray spiral) coincide.
Impact of dendritic length and diameter on Rm–dependence of the high-efficiency domain.
To study with sufficient resolution both the shape of the borders of the high-efficiency domain and the inequality of the corresponding shifts of the border toward the soma, relatively large decrements of Rm were required. Figure 3, which was obtained by using Equation 5, shows in detail how the path distance extent of the high-efficiency domain (Fig. 3, abscissas) was related to Rm in dendrites with equal diameters and different lengths (Fig. 3A) and with different diameters but equal lengths (Fig. 3B). In all cases, the plots were S-shaped, monotonically increasing functions. The top of each plot in Figure 3 defines a size-dependent maximum value of Rm = 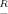 m, at which the high-efficiency domain extended to the distal dendritic end. The longer and/or the thicker the dendrite, the higher was this characteristic maximum value of
m, at which the high-efficiency domain extended to the distal dendritic end. The longer and/or the thicker the dendrite, the higher was this characteristic maximum value of 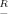 m. The bend point of each of the S-shaped curves defines another characteristic value of Rm = R*m. With increasing Rm, the slope of the plots first increased until R*m was reached and then decreased when Rm exceeded R*m. The variable slopes of the plots in Figure 3 indicate that the decrement of the extent of the high-efficiency domain was sensitive to Rm and that this sensitivity was location-dependent.
m. The bend point of each of the S-shaped curves defines another characteristic value of Rm = R*m. With increasing Rm, the slope of the plots first increased until R*m was reached and then decreased when Rm exceeded R*m. The variable slopes of the plots in Figure 3 indicate that the decrement of the extent of the high-efficiency domain was sensitive to Rm and that this sensitivity was location-dependent.
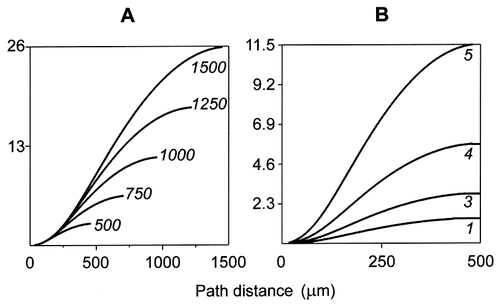
Relations between the path extent of the high-efficiency domain (abscissas) and Rm (ordinates) in dendrites with the same diameter (1.5 μm) but different lengths (A) or with the same length (500 μm) but different diameters (B). Numbers in A and B indicate the lengths and diameters in μm used for computing the corresponding plots. The variable slope of the plots demonstrates that the increment of the extent of the high-efficiency domain varies with the value of Rm (see text).
Sensitivity of the transfer effectiveness of uniform dendrite to changes in Rm.
The sensitivity function, S(x), defined by Equation 3 was computed for a dendrite of 1,500 μm with a diameter of 2 μm at different Rm values (Fig. 4). This function revealed which were the increments in the charge transfer effectiveness produced at different path distances from the soma by the same unitary increment of Rm. Spatial maps of this sensitivity function changed with changes in homogeneous Rm. When Rm was greater than a given characteristic value (≈10 kOhm.cm2 in this example), the sensitivity, S(x), was a monotonic increasing function of x. For the lower values of Rm, the sensitivity function had a maximum, and the path coordinate, x, of the maximum of S(x) was smaller for smaller Rm. Qualitatively similar behaviors of the sensitivity function took place in dendrites with other geometries.
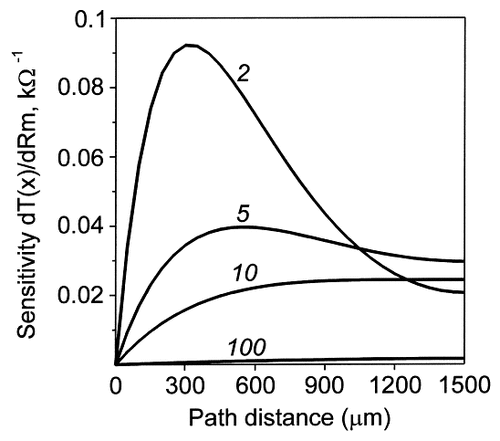
Path profiles of the sensitivity of the somatopetal charge transfer effectiveness to changes in the value of Rm. The sensitivity function (ordinate) is defined by Equation 1 (see Materials and Methods) and was computed with a dendrite with a length of 1,500 μm and a diameter of 2 μm. It is plotted as a function of the path distance from the soma (abscissa) for four values of Rm indicated in kOhm.cm2 above the corresponding plots. Maximum Rm sensitivity of the transfer effectiveness is observed at the dendritic tips under high Rm values (10 kOhm.cm2) and at intermediate dendritic lengths for lower Rm values (2 kOhm.cm2).
Reconstructed motoneurons
Comparative dendritic geometry of reconstructed motoneurons.
The selection of the four motoneurons was based on morphologic criteria (Fig. 5), which provided examples of cells with different total dendritic lengths and widely different individual dendrites in terms of their morphometric parameters (Fig. 6). The morphometric and topologic parameters of the arborizations are summarized in Table 1. The total number of dendritic branches was the smallest in the rat abducens motoneuron (n = 126 branches), whereas this number was more than doubled in the spinal motoneuron of rat (n = 282 branches), frog (n = 262 branches), and cat (n = 333 branches). The total dendritic length also was the smallest in the rat abducens motoneuron (11,931 μm). Among the spinal motoneurons, the total dendritic length was the shortest in the rat (20,803 μm), whereas it was greater in the frog (52,411 μm) and the cat (59,557 μm). The total dendritic area followed the same rule: It was smallest in the rat abducens motoneurons (39,257 μm2) and largest in the spinal motoneurons with the largest surface area for the cat (301,738 μm2). The index of complexity for each dendrite in the four motoneurons varied from 0 to 6.33. The highest complexity index (6.33) was found in one frog dendrite, and the lowest (0) characterized one dendrite in the frog and one in the rat abducens motoneurons. The coefficient of topologic asymmetry varied in the range of 0–0.75: It was highest in one dendrite of the rat abducens motoneuron.
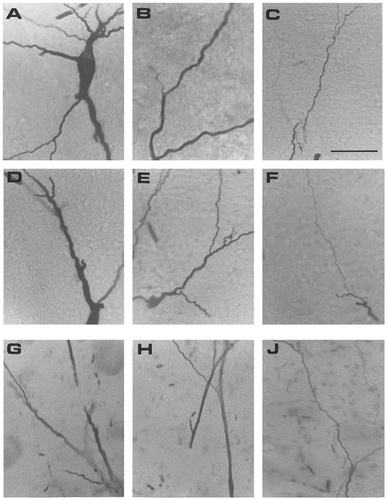
Photomicrographs of different morphologic details of frog (A–F) and cat (G–J) motoneurons stained intracellularly with horseradish peroxidase (shown in Fig. 6). A: Elongated soma with primary dendrites with different diameters. B,D,E: Examples of proximal dendrites (within 200 μm from soma) with bifurcations with daughter branches of similar diameters and very different diameters. C,F: Distal dendrites (>800 μm from soma) without spines. G,H: Proximal dendrites (within 200 μm from soma) with large bifurcations and rectilinear contours. J: Distal dendrites (>800 μm from soma) with different diameters. Photomicrographs of rat spinal and rat abducens motoneurons have been published elsewhere (Durand, 1989; Chmykhova et al., 1991). Scale bar = 50 μm.
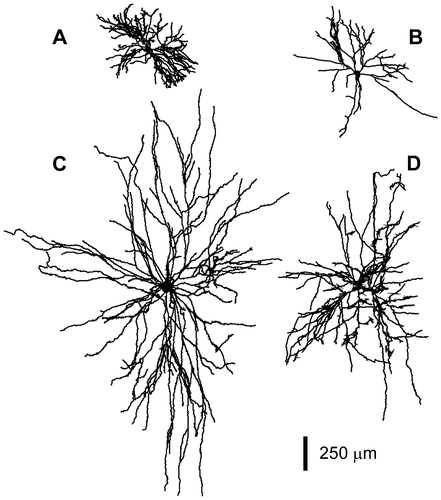
Two-dimensional representation of the four motoneurons reconstructed at high spatial resolution. A: Rat spinal motoneuron. B: Rat abducens motoneuron. C: Cat spinal motoneuron. D: Frog spinal motoneuron.
| No. dendrites | Branch no. | Dendrite length | Dendrite area | Complexity | Asymmetry |
|---|---|---|---|---|---|
| Rat spinal motoneuron | |||||
| 1 | 49 | 3,226.74 | 10,355.94 | 4.08 | 0.29 |
| 2 | 63 | 4,712.10 | 14,536.37 | 4.63 | 0.26 |
| 3 | 63 | 5,339.68 | 15,528.96 | 5.46 | 0.39 |
| 4 | 25 | 1,853.23 | 5,964.92 | 3.12 | 0.25 |
| 5 | 15 | 814.70 | 3,461.16 | 2.67 | 0.571 |
| 6 | 5 | 423.85 | 1,586.40 | 1.20 | 0.50 |
| 7 | 7 | 830.34 | 2,844.70 | 1.71 | 0.67 |
| 8 | 7 | 708.22 | 1,974.28 | 1.43 | 0.00 |
| 9 | 29 | 2,017.36 | 7,531.10 | 3.79 | 0.36 |
| 10 | 19 | 876.96 | 2,497.84 | 3.37 | 0.44 |
| Total | 282 | 20,803.18 | 66,281.67 | — | — |
| Rat abducens motoneuron | |||||
| 1 | 5 | 531.05 | 2,280.92 | 1.20 | 0.50 |
| 2 | 11 | 1,272.49 | 5,506.89 | 2.18 | 0.40 |
| 3 | 33 | 3,323.85 | 9,161.61 | 3.88 | 0.31 |
| 4 | 23 | 2,372.74 | 7,152.22 | 3.13 | 0.18 |
| 5 | 41 | 3,255.38 | 9,860.07 | 4.05 | 0.35 |
| 6 | 9 | 838.89 | 3,726.87 | 2.22 | 0.75 |
| 7 | 1 | 155.63 | 903.98 | 0.00 | 0.00 |
| 8 | 3 | 181.57 | 664.68 | 0.67 | 0.00 |
| Total | 126 | 11,931.60 | 39,257.24 | — | — |
| Cat spinal motoneuron | |||||
| 1 | 5 | 1,465.91 | 6,345.39 | 1.20 | 0.50 |
| 2 | 51 | 7,707.58 | 37,549.54 | 5.29 | 0.32 |
| 3 | 27 | 3,827.67 | 19,882.04 | 3.56 | 0.30 |
| 4 | 37 | 8,411.10 | 36,175.10 | 3.95 | 0.28 |
| 5 | 45 | 7,650.13 | 36,304.09 | 4.71 | 0.41 |
| 6 | 15 | 3,639.57 | 17,066.93 | 3.20 | 0.571 |
| 7 | 19 | 4,338.65 | 24,915.46 | 3.89 | 0.67 |
| 8 | 5 | 1,848.26 | 11,728.62 | 1.20 | 0.50 |
| 9 | 7 | 2,060.38 | 11,291.86 | 1.71 | 0.67 |
| 10 | 5 | 571.90 | 1,899.39 | 1.20 | 0.50 |
| 11 | 27 | 4,600.64 | 25,516.57 | 3.19 | 0.15 |
| 12 | 27 | 4,973.44 | 30,815.91 | 3.85 | 0.46 |
| 13 | 63 | 8,461.82 | 42,247.27 | 5.49 | 0.39 |
| Total | 333 | 59,557.05 | 301,738.17 | — | — |
| Frog spinal motoneuron | |||||
| 1 | 19 | 5,496.13 | 14,584.17 | 2.84 | 0.44 |
| 2 | 97 | 17,214.76 | 45,626.5 | 5.75 | 0.31 |
| 3 | 1 | 8.11 | 137.18 | 0.00 | 0.00 |
| 4 | 145 | 29,692.31 | 77,275.96 | 6.33 | 0.37 |
| Total | 262 | 52,411.31 | 137,624.06 | — | — |
- 1 See Figure 7.
An increase in the complexity of the dendritic arborizations occurred due to random occurrence of the branching points. The number of branching points occurred at different distances from soma and varied between motoneurons. The dendritic path lengths, i.e., the path distances from the somata to the dendritic tips, also showed important variations between motoneurons. The range of the variations was small in the rat spinal motoneuron, with a narrow distribution of >50% of the tips between 340 μm and 400 μm from the soma. In contrast, in the frog motoneuron, the distribution ranged over 1,873 μm, with several peaks around 600, 900, and 1,300 μm from the soma. In this metrically, very diversified motoneuronal sample, the same topology characterized one trio and three pairs of dendrites in the four motoneurons. Such dendrites had the same number of dendritic branches and the same branching patterns, as indicated by equal asymmetry and/or complexity indexes (Table 1). For instance, one dendritic pair included dendrite 5 of the rat and dendrite 6 of the cat spinal motoneurons, with the same number of branches (n = 15 branches) and the same index of topologic asymmetry (0.57) but with different metrical parameters. This pair of metrically different dendrites with equal topology was selected to study in detail the effect of metrical variance on their electrotonic structure.
Electrotonic reconfiguration of single reconstructed dendrites.
The dendrograms of the pair of dendrites are shown in Figure 7. The total path length of the branches was 3.5 times smaller in the rat (Fig. 7A) than in the cat (Fig. 7B). The path lengths varied from 250 μm to 345 μm in the rat and from 500 μm to 1477 μm in the cat. The diameters of the stem dendrites and their evolution along the dendritic paths also were very different. The electrotonic structures of both dendrites (Fig. 7) were computed at three different uniform specific membrane resistances (Rm = 100, 10, and 1 kOhm.cm2). The somatopetal charge transfer effectiveness (Tx), as expected, decayed with path distance from the soma in both dendrites under each Rm. The decay was smooth along uniform segments and sloped down at the sites of abrupt changes in diameter or asymmetrical branching. At bifurcations, the slopes of decay along asymmetrical sister branches were different, and the corresponding branching path profiles of Tx diverged. At any given dendritic site (x), Tx decreased when the values of Rm decreased from 100 kOhm.cm2 to 10kOhm.cm2 and 1 kOhm.cm2. Correspondingly, the path distances to the dendritic sites of a given effectiveness, Tx, decreased with decreasing Rm. Spatially homogeneous, equal decrements in the membrane resistivity produced spatially nonhomogeneous and unequal decrements in Tx. The decreases in Tx often were unequal at sites that were equidistant from the soma but located on different dendritic paths. These coupled geometry-dependent and Rm-dependent changes in the charge transfer effectiveness domain were similar qualitatively for any level of Tx. For the sake of simplicity, they are demonstrated here with one quantitative example in which the current transfer ratio was fixed at Tx = 0.5 (Fig. 7, horizontal dashed line). Thus, the dendritic branches of the two dendrites were divided into two domains of efficiency: one higher and one lower than Tx = 0.5. The entire dendrite from the rat motoneuron was in the high-efficiency domain at Rm = 100 kOhm.cm2 and 10 kOhm.cm2 but not at Rm = 1 kOhm.cm2, where the distal branches were in the low-efficiency zone over more than 125 μm (Fig. 7A, arrowheads). The entire dendrite from the cat motoneuron was in the high-efficiency domain only at 100 kOhm.cm2 and not at 10 kOhm.cm2 or 1 kOhm.cm2 (Fig. 7B). The arrowheads in Figure 7 indicate the dendritic sites with Tx = 0.5 defining the outer border of the high-efficiency domains. These border sites were not equidistant on different paths. It is noteworthy that, in the cat dendrite, the shortest branch was more efficient at 100 kOhm.cm2 and 10kOhm.cm2 than its much longer sister branch but became less effective at 1 kOhm.cm2.
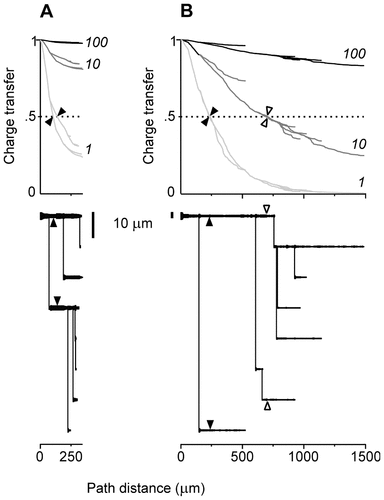
Reconfiguration of the electrotonic structures of two dendrites by changing the value of Rm. Dendrite 5 of the rat (A) and dendrite 6 of the cat (B) spinal motoneurons with the same number of branches (15) and the same asymmetry index (0.57) but with different metrical characteristics. Top: Somatopetal charge transfer effectiveness (ordinates) computed as a function of the path distance from soma (abscissas) under Rm = 100 kOhm.cm2 (black lines), 10 kOhm.cm2 (dark gray lines), and 1 kOhm.cm2 (light gray lines). When the value of Rm decreases, the path profiles of Tx also decrease, and the extent of the high-efficiency domains are reduced. Arrowheads indicate the dendritic sites, with Tx = 0.5 defining the outer borders of the high-efficiency domains. Bottom: Corresponding dendrograms of the dendrites with the same arrowheads delimiting the distal borders of the high-efficiency domains on the dendritic paths.
Electrotonic reconfiguration of the whole arborizations.
In each motoneuron, the electrotonic profiles representing the electrotonic structure of the whole dendritic arborizations displayed bundles that were more or less compact according to the value of Rm (Fig. 8). The bundles showed specific features for each arborization. The arbitrary partition of the arborizations into two domains of charge transfer effectiveness revealed that three of the four motoneurons had their whole arborization in the high-efficiency domain under Rm = 100 kOhm.cm2. The bundles of the shortest dendritic arborization (Fig. 8A) were the most compressed up to the distal tips, with values of Tx concentrated between 0.95 and 1.0, indicating a close similarity of all dendritic paths in their transfer effectiveness. The behavior of the rat abducens (Fig. 8B) and the cat motoneuron (Fig. 8C) was similar under Rm = 100, except for the longest path distances, in which a slight tendency toward decompression was observed in the cat. In the frog motoneuron (Fig. 8D), the electrotonic profiles were more decompressed even at Rm = 100, with some of the longest profiles in the low-efficiency domain. At Rm = 10 kOhm.cm2, all arborizations were decompressed, showing a much wider variation in the charge transfer effectiveness of the dendritic paths. Except for the rat spinal motoneuron, the longest profiles fell into the low-efficiency domain beyond 400–500 μm from the soma, some of them even reaching values close to zero efficiency at 1,500 μm from soma in the frog motoneuron (Fig. 8D). Because the rat spinal motoneuron (Fig. 8A) had no dendritic paths longer than 500μm, all of the profiles remained in the high-efficiency domain, although they were very decompressed in their distal parts, with a range of Tx between 0.93 and 0.56. Under Rm at 1 kOhm.cm2, a dramatic reduction in the high-efficiency domain characterized all arborizations. The bundles of profiles were compressed again in the four arborizations, and the slopes of Tx decreased abruptly over the first 250 μm from the soma to reach the low-efficiency domain. The longest path profiles of the cat and frog motoneurons fell to values close to zero efficiency between 550 μm and 700 μm from the soma, whereas none of the profiles of rat spinal or abducens motoneurons reached zero Tx even in their most distal parts.
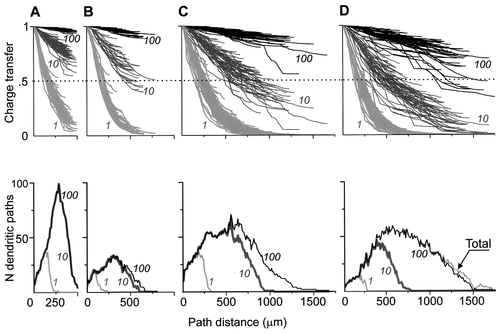
A–D: Reconfigurations of the electrotonic structures of the dendritic arborizations by changing values of Rm in the four motoneurones shown in Figure 5 and their complexity functions. Top: Electrotonic structures are represented by the path profiles of the somatopetal charge transfer effectiveness (abscissas) as a function of the path distance from soma (abscissas) computed for three values of Rm: 100 kOhm.cm2 (black lines), 10 kOhm.cm2 (dark gray lines), and 1 kOhm.cm2 (light gray lines). The profiles above and below the dotted line at Tx = 0.5 are situated in the low-efficiency (Tx < 0.5) and high-efficiency (Tx > 0.5) domains of the dendritic paths, respectively. The path coordinates of the cross points of profiles on the Tx = 0.5 line define the path distance from soma of the border of the high-efficiency domain of the corresponding dendritic paths. Bottom: The complexity function of the arborizations and their high-efficiency domains represented by the number of the dendritic path profiles (coordinates) with Tx > 0.5 at three values of Rm: 100 kOhm.cm2 (black line), 10 kOhm.cm2 (dark gray line), and 1 kOhm.cm2 (light gray line), as a function of the path distance from soma (abscissas). The number of profiles is equal to the number of dendritic paths, providing an estimate of the complexity of both the electrotonic profiles and the related dendritic domain. This integer estimate increments by 1 at a path distance where a branching occurs and decrements by 1 where a path or its high-efficiency domain portion ends. At Rm = 100 kOhm.cm2, entire arborizations were in the high-efficiency domain in all motoneurons (A–C) with only one exception (D). Their complexity function was superimposed on that of the entire arborizations (black lines). In D, the two functions display a slight difference (Total).
The reconfiguration of the electrotonic structures of the four motoneurons by different values of Rm revealed an unequal reduction in the high-efficiency domain of their arborizations. It also indicated clear quantitative differences between the sensitivity of Tx of each arborization to changes in Rm. The representation of the global electrotonic structure in physical coordinates provided a direct estimate of the proportion of the path extent in the high-efficiency domain, but the number of paths in this domain was not resolved because of the overlapping of electrotonic profiles in narrow bundles. To solve this problem, we used the fact that the dendritic branches and their corresponding bundles of electrotonic profiles were topologically homeomorphous. Here, we introduced a new complexity function to describe the dendritic domain of high efficiency.
New complexity function of the dendritic domains.
The complexity of any dendritic domain was defined by the number of dendritic paths as a function of the path distance from the soma. At 0 path distance, the complexity function was equal to the number of primary dendrites emerging from the soma. As the path distance increased, the number of paths increased by 1 when a bifurcation occurred or decremented by 1 when a path ended. The complexity function increased in the spatial domain where the branchings prevailed over terminals and decreased where the terminals prevailed.
The complexity function was used here to further characterize the number of dendritic branches included in the high-efficiency domain under the three values of Rm (Fig. 8, bottom). The surface area below the plots of the complexity function in Figure 8 showed the total length of the dendritic paths in the high-efficiency domain. For Rm = 100 kOhm.cm2, when the entire arborizations were highly effective in all but one of the three motoneurons, the complexity function was superimposed onto that of the whole arborization (Fig. 8, black lines), except in the frog motoneuron, in which a small difference was observed (Fig. 8D, black line and line marked Total). In the rat spinal motoneuron with path lengths that did not exceed 480 μm, the maximum complexity (99 paths) occurred at the shortest path distance of 280 μm (Fig. 8A). For the rat abducens motoneuron with a dendritic extension of 770 μm, the maximum complexity was smaller (35 paths) and occurred at 346 μm from the soma (Fig. 8B). In the cat spinal motoneuron, the maximum complexity (70 paths) occurred at about 540 μm, whereas the longest path was 1,627 μm (Fig. 8C). In the frog spinal motoneuron, the maximum complexity (60 paths) was at 470 μm from the soma, and the arborization extended up to 1,824 μm (Fig. 8D). The reduction in Rm to 10 kOhm.cm2 had no effect on the complexity function in the rat spinal motoneuron, whereas it decreased by ≈ 5%, 20%, and 60% in the other three motoneurons.
We concluded that the complexity function gave additional quantitative information that could not be retrieved from observation of the electrotonic profiles. The comparison of the frog and cat large spinal motoneurons, which displayed similar complexities at 10 kOhm.cm2 and 100 kOhm.cm2, showed a small difference in their maximum complexity functions, although there was a large reduction in the extent and the total length of the high-efficiency domains. In the two small motoneurons, the same changes in Rm introduced almost no changes in the complexity of their high-efficiency domains. However, a further reduction in Rm (1 kOhm.cm2) induced large changes in both path extent and complexity function in the four motoneurons. The complexity function ascertained that the high-efficiency domain can be reduced to a small number of dendritic branches efficiently connected to the soma under low values of Rm.
Mapping the high-efficiency domain onto the two-dimensional representation.
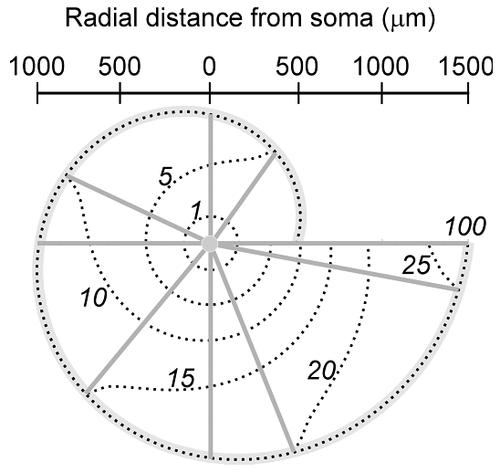
To ascertain further the variability in the high-efficiency domain and to provide a more functional picture, we computed it onto the two-dimensional representation of the motoneuronal arborizations, in which the projection fields of the dendrites were taken into account, and the variations in the radial field distances were the greatest (Fig. 9). With Rm at 1 kOhm.cm2, the number of dendritic branches efficiently connected to the soma decreased dramatically. The effective zone was reduced to a small ring around the soma in the large and small motoneurons. At Rm = 100 kOhm.cm2, the entire projection fields were in the high-efficiency domain, whereas, in between, (Rm = 10 kOhm.cm2), the large motoneuron with long dendritic paths had many distal branches in the low-efficiency domain compared with the small motoneuron. The larger the dendritic field, the greater was the variability of the high-efficiency domain.
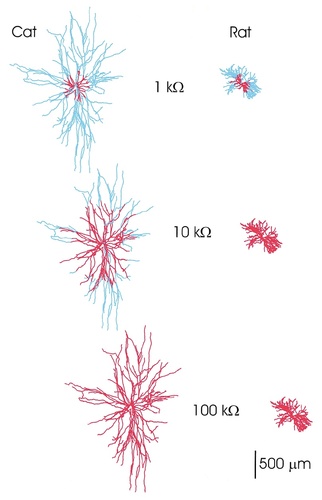
Maps of the high-efficiency domain (in red) of cat and rat spinal motoneurons for three values of Rm. At Rm = 100 kOhm.cm2, the dendritic fields of both arborizations are in the high-efficiency domain, with a similar weight for all synaptic inputs. By reducing the value of Rm, the high-efficiency domains shrink, and many dendritic branches are disconnected functionally from the soma. The cat motoneurons with long dendritic paths display a higher sensitivity to the reduction in the value of Rm, whereas the rat motoneurons with short dendritic paths are affected only by values of Rm < 10 kOhm.cm2. The switch from high values to low values of Rm in a neuron at rest compared with a highly excited neuron produces the functional reconfiguration of single motoneurons from an isodendritic type of dendritic field to an idiodendritic type of dendritic field (see Discussion).
DISCUSSION
Why metrical measurements need simulation
The theoretical approach in this study explains the impact of metrical parameters on the electrotonic structure of a simple tree. It analyzes the sensitivity of the electrotonic structure to changes in the value of Rm. In contrast to the structural complexity of the dendritic arborizations of neurons, the effect of each metrical parameter can be isolated and studied separately. Small and long, uniform, symmetrical, rectilinear dendrites; asymmetrical, rectilinear dendrites; dendrites with different lengths but similar diameters; and dendrites with different diameters but with similar lengths are considered to compute the charge transfer effectiveness of these simple elements as a function of different values of Rm. We also investigated how the efficiency domains of symmetrical and asymmetrical dendritic fields are reconfigured by changes in the value of Rm. Like any transfer characteristics in an electrical system, the relative changes in Tx can be characterized quantitatively by the function of sensitivity to Rm. Defined as the derivative of Tx over Rm, the sensitivity function (S) has the same branching path definition domain as Tx, and, like Tx, this function of the path also depend on Rm, the path length, and the parameters (see Eq. 1). We found that the maximum sensitivity is at the end of the dendritic path under the highest Rm and is greater at the end of a long path than at the end of a short path. Any decrease in Rm leads to a shift in the maximum of the sensitivity function to the proximal parts of the paths. Our computations reveal that the sensitivities of the proximal and distal sites are different. The maximum sensitivity occurs close to the soma at low Rm values, whereas the most distal dendritic sites are highly sensitive to changes in Rm at higher values. Due to such spatial properties of the sensitivity function, it is now possible to explain and predict differences in the variations of the size of the high-efficiency domain of the dendritic fields as function of changes in Rm. These findings on simple structures unmask the mechanisms by which the geometry governs the circulation of currents. They are basic to the understanding of the reconfiguration of the electrotonic structures of the most complex arborizations of live motoneurons.
Electrotonic structure of the dendritic arborizations of motoneurons
The most advanced quantitative descriptions of the dendritic morphology deal with the topology of the dendritic trees, offering topologic indices of asymmetry and complexity (Van Pelt et al., 1992; Verwer et al., 1992; Van Pelt and Schierwagen, 1994). Metrical descriptors are far less elaborated, although they are worth while. However, pure geometric descriptions may overlook functionally important features. The electrotonic structure that integrates structural and biophysical properties provides more reliable descriptions in terms of current flow circulating within the neuron. For example, unequal lengths of sister dendritic paths can be considered as metrical asymmetry. It was proved to be a key factor to differentiate the electrotonic transfer effectiveness between dendritic paths (Bras et al., 1993; Korogod, 1996). In this work, we show that the same asymmetrical topology of the dendrites is not sufficient in itself to sustain an electrotonic similarity. This conclusion is supported by the fact that the dendrites with the same number of branches and topologic asymmetry index but with very different branch lengths also displayed very different electrotonic structures. The observation that these electrotonic structures are sensitive differentially to changes in Rm is a novel aspect of the functional consequences of electrogeometric coupling in branching dendrites.
The dendritic arborizations of motoneurons differ greatly in their spatial extensions and in the variability of their path lengths. Because Rm defines transmembrane loss of current transferred to the soma, all of the dendritic path would be equally noneffective at 0 Rm and 100% effective at infinite Rm. In these two limiting cases, all electrotonic profiles coincide at Tx = 1 or 0. At intermediate Rm, the profiles of Tx diverge only along asymmetrical paths and, thus, are resolved. For a given asymmetrical arborization, there is a quantitative optimum value of Rm with which the path profiles of the current transfer are resolved best. In defining the features of transformations of the electrotonic structure with reference to morphology, our findings explain why the different arborizations display different rates of decrease of charge transfer. According to the sensitivity function, the greatest rate of diminution is expected in the longest profiles of the frog dendrites when observed at Rm = 100 kOhm.cm2. Consequently, the profiles along much shorter and less variable dendrites of the rat spinal motoneuron are decreasing only slightly in this range of membrane resistivity. At Rm = 1 kOhm.cm2, many distal path profiles of the longest frog dendrites overlap at Tx = 0 as they achieve a sensitivity of zero. The much shorter and wider separated rat spinal and abducens dendrites remain above zero sensitivity in this range of Rm.
We conclude that the variability of the high-efficiency domain under the same changes in Rm clearly is related to differences in the lengths of dendritic branches and in the branching pattern. The greater the metrical and topologic asymmetry, the greater are the differences between arborizations.
Complexity function
The differential Rm sensitivity of the charge transfer effectiveness raises the question of a quantitative description of the complexity of both geometric and electrotonic structures. In this study, we express the problem functionally in terms of effective sizes and shapes of the dendritic fields delimited by a given level of Tx as a function of the path distance from the soma. In the conventional two-dimensional representation of such electrotonic characteristics as the transmembrane voltage and the charge transfer effectiveness, the path behavior is masked as their plots as a function of the path distance are intermingled. To cope with the problem of quantitative estimations of the dendritic path structure of both the entire dendritic fields and their high-efficiency domains, we introduce the complexity function. When it is represented graphically with the same abscissas (the path distance from the soma), the complexity function indicates directly how many dendritic paths or path profiles of Tx are at a given path distance. This function also shows how the complexity is modified by branching or termination of the paths and/or profiles. Another advantage of this function is that it is additive. If an arborization is divided into arbitrary parts, then the complexity function of the whole arborization is the sum of the complexity function of the parts. Thus, the comparison of the complexities of different domains of the same arborization or of different arborizations is coherent. In this work, we describe quantitatively the complexity of electrotonic high-efficiency domains under different values of Rm. Our results show that similar modifications in the complexity function are observed in small motoneurons and large motoneurons. An unexpected result is the finding that the switch from high Rm to low Rm eliminates a strikingly high number of dendritic paths from the high-efficiency domain. Thus, only small numbers of branches remain connected functionally to the soma. This dynamic shift is illustrated best in the two-dimensional representations of the motoneuronal dendritic fields.
Functional consequences of the dynamics of the dendritic fields
The anatomy of dendritic fields of motoneurons has been studied extensively since Ramon y Cajal (1911). It represents ≈95% of the total somatodendritic surface area of the motoneuron that receives thousands of synapses distributed spatially over the dendrites (Brännström, 1993; Alvarez et al., 1998). The dendritic surface area is related directly to the variety of afferent systems that impinge on the motoneurons. This anatomic notion has never been questioned in terms of the dynamic functionality of the motoneurons. Does the dendritic field of the motoneurons vary in size and shape according to the state of the neuronal activity? A neuron never exists in isolation but is embedded in a heavily interconnected network of neurons that are active spontaneously. Does the synaptic background activity have an impact on the spatial integrative properties of the dendritic structure? Can it modulate the size and shape of the dendritic field by tuning the specific resistance of the receiving dendritic membrane? It is now generally admitted that the input resistance of the neuron RN and Rm are related directly to the level of synaptic bombardment that the neuron receives (Barrett and Crill, 1974; Holmes and Woody, 1989). In a recent work, Paré et al. (1998) demonstrate that RN is reduced markedly during intense synaptic bombardment of cat neocortical neurons in vivo.
In this last part of the Discussion, we refer to a neuron at rest for the results obtained under Rm = 100 kOhm.cm2 and to a highly excited neuron for those under Rm = 1 kOhm.cm2. Because the total current reaching the initiation zone of the action potentials is one key parameter for the output discharges of the motoneuron, the notion of a highly effective domain fixed above 0.5 of Tx is proposed. Any values of Tx between 0.1 and 1.0 may have been chosen, because this value is not critical for the demonstration. Although this is a purely arbitrary value, it is useful to compare the efficiency of each dendritic path to control the motoneuronal output at a given moment and for a given state of excitability. Moment-to-moment variations in Tx according to the background synaptic activity are expressed by the sensitivity function (see Fig. 4).
The striking result of our study is the finding that the size and shape of the effective dendritic field vary as a function of the background activity of the brain. In the excited neuron, all distal parts of the dendrites are disconnected functionally from soma in large motoneurons. In small motoneurons, the distal dendrites also are switched into the low-efficiency domain. The proximal dendrites that remain within the ring of the high-efficiency zone have variable spatial limits related to the size of the motoneurons. At rest, the large and small motoneurons behave the same, with all of their dendrites in the high-efficiency domain. The only difference is that the large structures are more sensitive to variations in the upper range of the membrane resistance, thus disconnecting the distal dendrites before the small motoneurons. Between these two extreme situations—at rest and highly excited—any situation can occur that is a mixture of the extreme cases. The interesting feature of these in-between cases is the extreme variability of the borders of the high-efficiency domain in the dendritic fields. The ring of high efficiency is larger in size and mostly is asymmetrical in large motoneurons.
The two extreme situations are characterized by a similar efficiency or inefficiency of all dendritic paths to transfer current to the soma without any spatial discrimination. The same synaptic inputs are processed similarly, regardless of the receiving dendritic branch, and have similar effects on the output discharge. In the in-between situations, in which the neuron is not fully excited but is not at rest, the dendritic fields explode from compactness into a large repertoire of different path profiles with low and high efficiency to transfer charges. In the same dendrite, one sister branch may occupy the high-efficiency domain, whereas the other branch may occupy the low-efficiency domain. Here, the spatial discrimination is extremely high if the same synaptic inputs reach dendritic sites in the high- or low-efficiency domains. These in-between conditions provide the dendrites with subtle capabilities to discriminate between synaptic inputs and to select or ignore some of them. This depends on the spatial repartition of some synapses, even on a small part of the tree. What is most remarkable is the dynamics of the same anatomic structure, which can switch from a highly discriminative, unstable state to a “ready-to-respond system,” according to the actual state of activity of the neuronal networks.
We demonstrate that these reconfigurations of the dendritic fields that expand or shrink are geometry- and activity-dependent. We suggest that the geometry confers its stability to the system. Its dynamics rely on the microstructure of the dendritic membrane, which is encrusted by voltage-gated channels that are distributed spatially in the dendritic arborizations and on the synaptic bombardment that they receive.
Motoneurons in their networks
The data describing the distribution of synapses over the dendritic membrane of the motoneurons are scarce, even if evaluations of the synaptic density and the synaptic covering on the soma and proximal dendrites exist (Conradi, 1969; Burke et al., 1971; Conradi et al., 1979; Kellerth et al., 1983; Lagerbäck, 1985; Bras et al., 1987b; Fyffe, 1991; Antal et al., 1992). An extensive quantitative study of the synaptology of different types of α-motoneurons by Brännström (1993) presented new data on the synaptic covering of the dendritic trees. However, little information is available regarding the precise spatial distribution over the entire dendritic arborizations of the variety of afferent synaptic systems that a motoneuron receives. The only quantitative data available concern the Ia afferents in the spinal motoneurons of the cat (Brown and Fyffe, 1978, 1981; Pierce and Mendell, 1993; Burke and Glenn, 1996) and the frog (Jackson and Frank, 1987). Contacts between vestibulospinal axon terminals and dendrites of the neck motoneurons have been described in a nonuniform arrangement that depends on the orientation of the dendrites (Rose et al., 1995). Secondary vestibular axon terminals onto the abducens motoneurons also have been described in the proximal dendrites (Ohgaki et al., 1988; Pekinat et al., 1986). In contrast, serotoninergic terminals have been described as distributed widely in the cat arborizations of the spinal motoneurons (Alvarez et al., 1998). Moreover, synaptic efficacy remains an open question for which no direct evidence allows the selection of pertinent parameters. For example, a recent theoretic paper showed that the size of the synaptic cleft and the spatial distribution of the receptors determine the synaptic current (Savtchenko et al., 1999). Obviously, an adequate analysis of our findings could be made only if it was possible to ascertain the origin, spatial distribution, and functional modality of all afferent systems terminating in single motoneurons. In the absence of such detailed information, only earlier physiologic results can be considered.
It is known that spinal motoneurons receive highly specific inputs from muscles, joints, and skin in the periphery through a complex network of spinal interneurons (for reviews and references, see Granit and Pompeiano, 1979). Physiologists have long known that motor systems operate according to a descending cascade of controls, including some that affecting the motoneurons that receive descending inputs from vestibulospinal, reticulospinal, and corticospinal tracts. From the operational concepts of the brainstem reticular systems, there emerged the notions of nonspecific systems that modulate the spinal motor activity as well as the states of consciousness from deep sleep to maximal vigilance (for reviews and references, see Livingston, 1967; Scheibel and Scheibel, 1967). More recently, intracellular recordings from lumbar motoneurons in unanesthetized undrugged cats have shown that depolarizing and hyperpolarizing shifts occur in the membrane potential during the rapid-eye-movement periods of active sleep (Soja et al., 1991, 1995).
The speculation that the specific inputs are distributed mostly on the proximal dendrites and the nonspecific systems shower the entire dendritic fields with different types of synaptic inputs often has been suggested. According to our findings, the dendritic field that shrinks in the highly excited neuron selects and favors only the specific messages from the muscles and other sensory peripheral regions. Thus, the motoneuron becomes specialized in specific motor tasks. Returning to the resting state, the motoneuron enhances its potentialities to process more diversified, nonspecific systems. Classical observations, such as muscular tone, posture, decerebrate rigidity (Granit and Pompeiano, 1979), and reticular motor control during different states of wakefulness (Magoun, 1954; Moruzzi, 1954), may be revisited with this new notion of the dynamics of the dendritic fields.
In earlier anatomic works (Ramon-Moliner, 1962; Ramon-Moliner and Nauta, 1964), a classification of the nerve cells was based on their dendritic patterns. The sharp distinction between cell regions that exhibit “generalized” dendritic features on the one hand and some well-defined, secondary sensory nuclei that display “specialized” dendritic characteristics on the other hand was used. New terms were introduced (Mannen, 1960; Leontovich and Zhukova, 1963), such as isodendritic and idiodendritic structures. The isodendritic area described a vast region that extended throughout the brainstem and the spinal cord. The other term, idiodendritic, referred to specialized dendritic patterns. It was discussed whether the idiodendritic neurons, with their specialized dendrites, could be related to a high degree of homogeneity of the inputs corresponding to a reduction in the number of functional potentialities. In contrast, the isodendritic neurons would be associated with diversified connections with increased functional properties.
Our findings suggest a possibility in which both diffuse functions and specific functions may be performed by the same motoneuron. It could be assumed that the proximal parts of the dendrites are involved in the collection of specific messages that are coded in terms of an output type of response, whereas the most distal dendrites could receive information regarding the overall activity of the neuronal networks. The activity-dependent dynamics of the dendritic field of single neurons would regulate its functional size and shape in such a manner that a single neuron could be isodendritic and idiodendritic, alternatively, according to the general state of the brain.
Acknowledgements
The authors are grateful to Drs. Dityatev, Chmykhova, Bras, and Jankowska for generously providing raw data on motoneurons. They thank Dr. C. Batini and Dr. E. Jankowska for criticisms of the paper and Dr. P.K. Rose for his invaluable advice and comments on the paper. I.B.K. was supported by scholarship from the Service Culturel de l'Ambassade de France à Kiev en Ukraine. The program NEURON (by J.W. Moore of Duke University Medical Center and M. Hines of Yale University; Yale University, 1994) was obtained from a public WWW domain at Yale University.




